目录
1. 🔍稳定性
两个相等的数据,如果经过排序后,排序算法能保证其相对位置不发生变化,则我们称该算法是具备稳定性的排序算法。
44 2 a1?4 63 56 a2?34? 排序后?2 a1?4 34 44 63 56 a2?相对位置没有发生变化
2.🔍冒泡排序
public void bubbleSort(int[] arr){
//最外层表示要比较的趟数,arr.length - 1,- 1 是因为当待排序数组只剩一个元素时,此时数组已经有序
for (int i = 0; i < arr.length - 1; i++) {
boolean flag = true;
for (int j = 0; j < arr.length - i - 1; j++) {
if(arr[j] > arr[j + 1]){
swap(arr,j,j + 1);
flag = true;
}
}
if(flag == false){
//内层循环没有元素交换,整个数组有序
break;
}
}
}时间复杂度:O(N^2)? ? 无论是好是坏都是?O(N^2)?
空间复杂度:O(1)?
稳定
3. 🔍插入排序
整个区间被分为 有序区间 和 无序区间每次选择无序区间的第一个元素,在有序区间内选择合适的位置插入
public void insertSort(int[] array) {
for(int i = 1; i < array.length; i++) {
int tmp = array[i];
int j = i - 1;
for(; j >= 0; j--) {
if(array[j] > tmp) {
array[j + 1] = array[i]; //将前一个数与后一个数交换位置
} else {
break;
}
}
array[j + 1] = tmp;
}
}?时间复杂度:O(N^2)?
空间复杂度:O(1)?
稳定
直接插入排序,有序情况下是O(N),因为,当 array[j] > tmp时,直接break,j不会再次--。
3.1??🚀折半插入排序
在已经有序的数组中插入一个数(常用在数据量不多,区域有序的数据中)
假设现在有10000个数,如果对这组数据进行排序,使用插入排序。
10000个数据的时间复杂度:10000 * 10000 = 10000 0000
10000个数据 = 100组 * 100个 ,分100组,每一组的时间复杂度为100 * 100 = 10000
由此可以发现,分组使得时间复杂度有很大的改变。
4. 🔍希尔排序
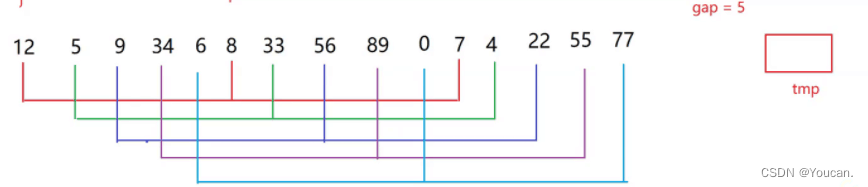
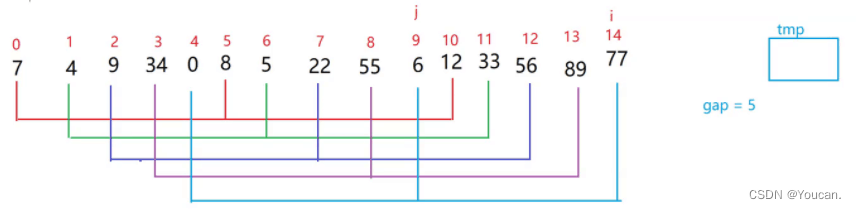
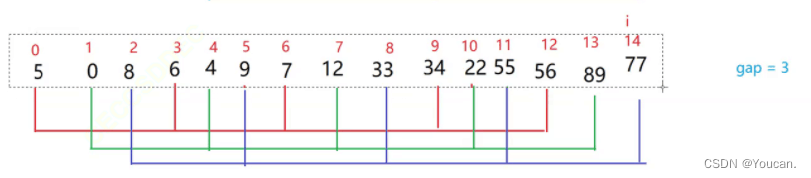
又称缩小增量法。先选定一个整数,把待排序文件中所有记录分成 n 个组,所有距离为n 的记录分在同一组内,并对每一组内的记录进行排序。然后重复上述分组和排序的工作。当分组等于1时,所有记录在统一组内排好序。
1. 希尔排序是对直接插入排序的优化。2. 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就会很快。这样整体而言,可以达到优化的效果。
?
?
?
?
public static void shellSort(int[] array) {
int gap = array.length;
while(gap > 1) {
shell(array, gap);
gap /= 2;
}
shell(array, 1); //保证最后是1组,对整个数组进行排序
}
public static void shell(int[] array, int gap) {
for(int i = 1; i < array.length; i++) {
int tmp = array[i];
int j = i - gap;
for(; j >= 0; j -= gap) {
if(array[j] > tmp) {
array[j + 1] = array[j];
} else {
break;
}
}
array[j + gap] = tmp;
}
}?时间复杂度:O(N^1.3 ~ N^1.5)
空间复杂度:O(1)?
不稳定
在比较的过程中,看是否发生跳跃式的交换,如果是跳跃式的,则就是不稳定的排序。?
5. 🔍选择排序
?每一次从无序区间选出最大(或最小)的一个元素,存放在无序区间的最后(或最前),直到全部待排序的数据元素排完。
public static void selectSort(int[] array) {
for(int i = 0; i < array.length; i++) {
for(int j = i + 1; j < array.length; j++) {
if(array[j] < array[i]) {
swap(array,j,i);
}
}
}
}
public static void swap(int[] array, int i, int j) {
int tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
时间复杂度:O(N^2)
空间复杂度:O(n)?
不稳定
?直接插入排序,有序情况下是O(N),因为,当 array[j] > tmp时,直接break,j不会再次--。
选择排序来说,有序无序都是O(N^2) ,因为时间复杂度 !=运行时间。在有序的情况下,选择排序的时间更快,j++不会因此减少。
6. 🔍堆排序
?排升序要建大堆;排降序要建小堆
?调整为大根堆,最大值一定在堆顶,将其与末尾元素进行交换,此时末尾元素就位最大值,然后将剩余的n - 1 个元素重新构造称为一个堆,依次执行该步骤。
public void heapSort(int[] arr){
//1.将任意将数组进行原地排序
//从最后一个非叶子结点开始,即就是最后一个叶子节点的父节点
//最后一个叶子结点arr.length - 1 , 父节点(arr.length - 1 - 1)/2
for (int i = (arr.length - 1 - 1) / 2; i >= 0 ; i--) {
siftDown(arr,i,arr.length);
}
//依次取出堆顶元素和最后位置元素进行交换
//最开始,待排序的数组[0......arr.length - 1],已排序的数组[]
//第二次,待排序的数组[0......arr.length - 2],已排序的数组[arr.length - 1]
//第三次,待排序的数组[0......arr.length - 3],已排序的数组[arr.length - 2,arr.length - 1]
//......
//此处i > 0,不用写i = 0,因为当数组中只剩一个元素时,数组已经有序
for (int i = arr.length - 1; i > 0 ; i--) {
//第0个元素,与最后一个元素进行交换
swap(arr,0,i);
//最后一个元素不需要考虑下沉
siftDown(arr,0,i);
}
}
/**
* 元素下沉操作
* @param arr
* @param i 父节点
* @param n 当前arr中有效元素个数
*/
private void siftDown(int[] arr, int i, int n) {
//终止条件:仍然存在子树(子树小于有效元素的个数)
while((2 * i) + 1 < n){
int j = 2 * i + 1;
//右孩子存在且大于左子树
if(j + 1 < n && arr[j + 1] > arr[j]){
j = j + 1;
}
if(arr[i] >= arr[j]){
break;
}else {
swap(arr,i,j);
i = j;
}
}
}时间复杂度:O(N * logN)
空间复杂度:O(1)?
不稳定
7. 🔍快速排序(挖坑法)
1. 从待排序区间选择一个数,作为基准值(pivot);2. Partition: 遍历整个待排序区间,将比基准值小的(可以包含相等的)放到基准值的左边,将比基准值大的(可以包含相等的)放到基准值的右边;3. 采用分治思想,对左右两个小区间按照同样的方式处理,直到小区间的长度 == 1,代表已经有序,或者小区间的长度 == 0,代表没有数据。
(优化算法)基准的找法:
? 三数取中法
? 随机法
? 把和基准相同的数据,从两边移到一起
? 利用直接插入排序
public static void quickSort(int[] array) {
quick(array,0,array.length - 1);
}
public static void quick(int[] array, int left, int right) {
if(left >= right) {
return;
}
int pivot = partition(array, left, right);
quick(array,left,pivot - 1);
quick(array,pivot + 1, right);
}
private static int partition(int[] array, int start, int end) {
int tmp = array[start];
while(start < end) {
while(start < end && array[end] >= tmp) {
//start < end 加入有 12345,end--会使得end < start ,所以仍要加这个条件
end--;
}
array[start] = array[end];
while(start > end && array[start] <= tmp) {
start++;
}
array[end] = array[start];
}
array[start] = tmp;//此时start和end相遇
return start;
}
?时间复杂度:O(N * logN) (相当于二叉树,二叉树的每一层都是n)
空间复杂度:O(logN)? ?(递归,要保留之前的状态)?
不稳定
?时间复杂度:
? ? ? ? 最好情况:每次可以均匀的分割待排序序列 O(N * logN)?
????????最坏情况:数据有序,或者逆序的情况O(N^2)
空间复杂度:
????????最好情况: O(logN)?
????????最坏情况:单分支的一棵树O(N)?
8. 🔍归并排序
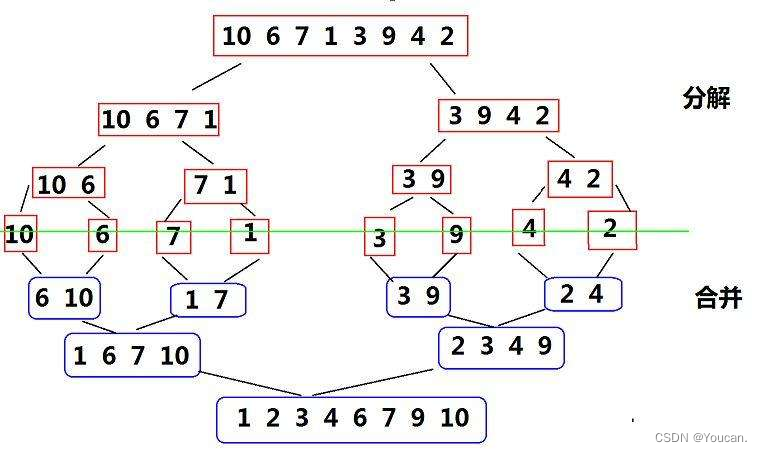
?归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
public static void mergeSort(int[] array) {
mergeSortInternal(array, 0, array.length - 1);
}
private static void mergeSortInternal(int[] array, int low, int high) {
int mid = low + ((high - low) >>> 1);
mergeSortInternal(array, low, mid);
mergeSortInternal(array, mid + 1, high);
merge(array, low, mid, high);
}
private static void merge(int[] array, int low, int mid, int high) {
int[] tmp = new int[high - low + 1];
int k = 0;
int s1 = low;
int e1 = mid;
int s2 = mid + 1;
int e2 = high;
while(s1 <= e1 && s2 <= e2) {
if(array[s1] <= array[s2]) {
tmp[k++] = array[s1++];
} else {
tmp[k++] = array[s2++];
}
}
while(s1 <= e1) { // 此时s2已经遍历完
tmp[k++] = array[s1++];
}
while(s2 <= e2) {
tmp[k++] = array[s2++];
}
for (int i = 0; i < k; i++) { //将tmp中的数组元素拷贝到原来的array中
array[i + low] = tmp[i];
}
}?
?时间复杂度:O(N * logN)?
空间复杂度:O(N)?
稳定
?9.?🔍海量数据的排序问题
内存只有 1G,需要排序的数据有 100G因为内存中因为无法把所有数据全部放下,所以需要外部排序,而归并排序是最常用的外部排序1. 先把文件切分成 200 份,每个 512 M2. 分别对 512 M 排序,因为内存已经可以放的下,所以任意排序方式都可以3. 进行 200 路归并,同时对 200 份有序文件做归并过程,最终结果就有序了
?