AcWing 1017. 怪盗基德的滑翔翼
输入样例：
3 8 300 207 155 299 298 170 158 65 8 65 158 170 298 299 155 207 300 10 2 1 3 4 5 6 7 8 9 10输出样例：
6 6 9
当确定完方向和起点完后，最长的距离是什么呢？
起点：a[i]
最长：以?a[i]?为起点的最长上升子序列 （LIS）
#include <iostream> #include <algorithm> using namespace std; const int N = 110; int n; int a[N], f[N]; int main() { int T; cin >> T; while(T -- ) { cin >> n; for(int i = 1; i <= n; i ++ ) scanf("%d", &a[i]); // 正向求解 LIS int res = 0; for(int i = 1; i <= n; i ++ ) { f[i] = 1; for(int j = 1; j < i; j ++ ) if(a[i] > a[j]) f[i] = max(f[i], f[j] + 1); res = max(res, f[i]); } // 反向求解 LIS for(int i = n; i; i -- ) { f[i] = 1; for(int j = n; j > i; j -- ) if(a[i] > a[j]) f[i] = max(f[i], f[j] + 1); res = max(res, f[i]); } cout << res << endl; } return 0; }
AcWing 1014. 登山?
输入样例：
输出样例：
4
题目中有以下条件：
- 按照编号递增的顺序来浏览（子序列）
- 相邻的两个景点不能相同高度（严格单调）
- 一旦开始下降就不能上升?
目标：求最多能浏览多少景点
两个LIS然后求解出相加最大值
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n;
int a[N];
int f[N], g[N];
int main()
{
cin >> n;
for(int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
for(int i = 1; i <= n; i ++ )
{
f[i] = 1;
for(int j = 1; j < i; j ++ )
if(a[i] > a[j])
f[i] = max(f[i], f[j] + 1);
}
for(int i = n; i; i -- )
{
g[i] = 1;
for(int j = n; j > i; j -- )
if(a[i] > a[j])
g[i] = max(g[i], g[j] + 1);
}
int res = 0;
for(int i = 1; i <= n; i ++ ) res = max(res, f[i] + g[i] - 1);
cout << res << endl;
return 0;
}AcWing 1012. 友好城市
输入样例：
7 22 4 2 6 10 3 15 12 9 8 17 17 4 2输出样例：
4
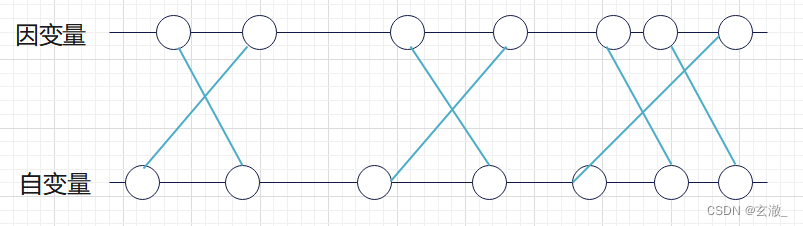?所有合法的建桥方式都对应着一个因变量的上升子序列
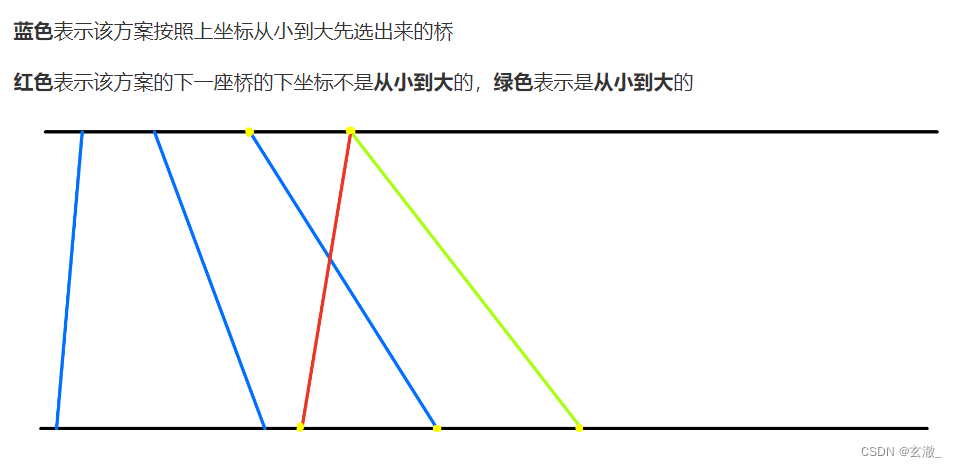
?因此，该方案中，在上坐标排序的情况下，下坐标次序不是从小到大的，则必然不合法（会有相交）
于是，这题就变成了：桥以上坐标从小到大排序后，找出下坐标的最长上升子序列长度
#include <iostream> #include <cstring> #include <algorithm> using namespace std; const int N = 5010; typedef pair<int, int> PII; int n; PII q[N]; int f[N]; int main() { cin >> n; for(int i = 0; i < n; i ++ ) scanf("%d%d", &q[i].first, &q[i].second); sort(q, q + n); int res = 0; for(int i = 0; i < n; i ++ ) { f[i] = 1; for(int j = 0; j < i; j ++ ) if(q[i].second > q[j].second) f[i] = max(f[i], f[j] + 1); res = max(res, f[i]); } cout << res << endl; return 0; }
AcWing 1016. 最大上升子序列和?
输入样例：
7 1 7 3 5 9 4 8输出样例：
18
?
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n;
int a[N], f[N];
int main()
{
cin >> n;
for(int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
for(int i = 1; i <= n; i ++ )
{
f[i] = a[i];
for(int j = 1; j < i; j ++)
if(a[j] < a[i])
f[i] = max(f[i], f[j] + a[i]);
}
int res = 0;
for(int i = 1; i <= n; i ++ ) res = max(res, f[i]);
cout << res << endl;
return 0;
}AcWing 1010. 拦截导弹?
输入样例：
389 207 155 300 299 170 158 65输出样例：
6 2
这道题的第一问是一个经典的 LIS 问题
对于第二问，我们采用贪心思路
贪心流程：
从前往后扫描每个数，对于每个数：
? ? ? ? 情况1：如果现有的子序列的结尾都小于当前数，则创建新的子序列
? ? ? ? 情况2：将当前数放到大于等于它的最小的子序列后面
贪心证明：
1.如何证明两个数相等？?
?A 表示贪心算法得到的序列个数，B 表示最优解
?①?
，由最优解的性质可得
?②?
?调整法
? ? ? ??假设最优解对应的方案和当前方案不同
? ? ? ? 找到第一个不同数。
? ? ? ? 通过有限次的交换可以将最优解调整为贪心解，且不增加序列个数
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n;
int q[N];
int f[N], g[N];
int main()
{
while(cin >> q[n]) n ++ ;
int res = 0;
for(int i = 0; i < n; i ++ )
{
f[i] = 1;
for(int j = 0; j < i; j ++ )
if(q[j] >= q[i])
f[i] = max(f[i], f[j] + 1);
res = max(res, f[i]);
}
cout << res << endl;
int cnt = 0;
for(int i = 0; i < n; i ++ )
{
int k = 0;
while(k < cnt && g[k] < q[i]) k ++ ;
g[k] = q[i];
if(k >= cnt) cnt ++ ;
}
cout << cnt << endl;
return 0;
}?AcWing 272. 最长公共上升子序列
4 2 2 1 3 2 1 2 3输出样例：
2
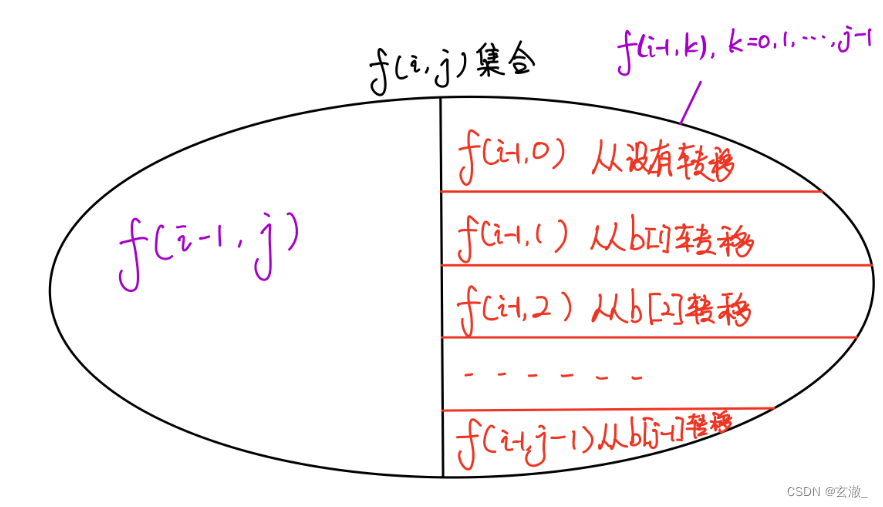
这道题目是最长上升子序列和最长公共子序列的结合版，在状态表示和状态计算上都是融合了这两道题目的方法。
状态表示：
?代表所有 a[1 ~ i] 和 b[i ~ j] 中以 b[j] 结尾的公共上升子序列的集合
的值等于该集合的子序列中长度的最大值?
状态计算：
首先根据公共子序列中是否包含a[i]，将 f[i][j] 所代表的集合分成两个不重不漏的子集
- 不包含 a[i] 的子集，最大值是 f[i - 1][j]
- 包含a[i] 的子集，将这个子集继续划分，依据是子序列的倒数第二个元素在 b[] 中是哪个数
- 子序列只包含 b[j] 一个数，长度是1
- 子序列的倒数第二个数是 b[1] 的集合，最大长度是 f[i-1][1] + 1
- ....
- 子序列的倒数第二个数是 b[j - 1] 的集合，最大长度是 f[i-1][j-1] + 1
得到以下?的做法
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 3010;
int n;
int a[N], b[N];
int f[N][N];
int main()
{
cin >> n;
for(int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
for(int i = 1; i <= n; i ++ ) scanf("%d", &b[i]);
for(int i = 1; i <= n; i ++ )
for(int j = 1; j <= n; j ++ )
{
f[i][j] = f[i - 1][j];
if(a[i] == b[j])
{
f[i][j] = max(f[i][j], 1);
for(int k = 1; k < j; k ++ )
if(b[k] < b[j])
f[i][j] = max(f[i][j], f[i][k] + 1);
}
}
int res = 0;
for(int i = 1; i <= n; i ++ ) res = max(res, f[n][i]);
cout << res << endl;
return 0;
}然后我们发现每次循环求得的maxv是满足a[i] > b[k]的f[i - 1][k] + 1的前缀最大值。
因此可以直接将maxv提到第一层循环外面，减少重复计算，此时只剩下两重循环。
最终答案枚举子序列结尾取最大值即可。
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 3010;
int n;
int a[N], b[N];
int f[N][N];
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
for (int i = 1; i <= n; i ++ ) scanf("%d", &b[i]);
for (int i = 1; i <= n; i ++ )
{
int maxv = 1;
for (int j = 1; j <= n; j ++ )
{
f[i][j] = f[i - 1][j];
if (a[i] == b[j]) f[i][j] = max(f[i][j], maxv);
if (a[i] > b[j]) maxv = max(maxv, f[i - 1][j] + 1);
}
}
int res = 0;
for (int i = 1; i <= n; i ++ ) res = max(res, f[n][i]);
printf("%d\n", res);
return 0;
}