二叉树的遍历操作
(以下图片参考懒猫老师《数据结构》相关课程的笔记,作学习笔记,用C语言实现)
以下图二叉树为例:
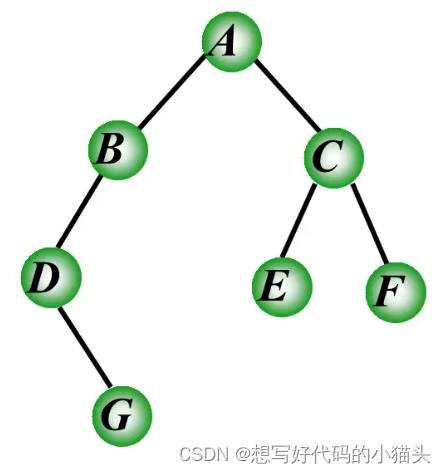
这里使用的二叉树存储结构是二叉链表,数据结构如下:
typedef struct binarytree{
Datatype data;//数据内容
struct binarytree* Lchild;//指向左孩子结点
struct binarytree* rchild;//指向右孩子结点
}binarytree;在进行遍历的算法之前,先简单说一下二叉链表的构建 ~
首先先介绍以下扩展二叉树的概念,就是在为NULL的左右孩子上填充'#',如下图:
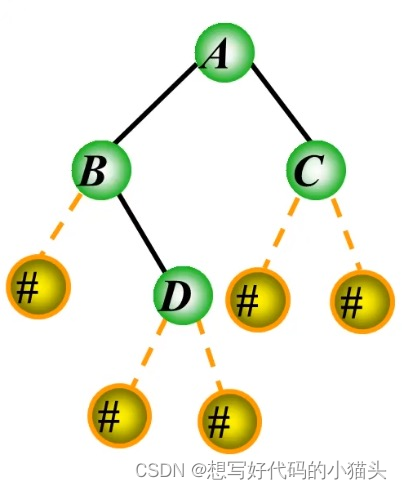
设二叉树中的结点均为—个宇符。假设扩展二叉树的前序遍历序列由键盘输入,root为指向根结点的指针,二叉链表的建立过程是:
首先输入根结点,若输入的是一个“#”字符,则表明该二叉树为空树,即root==NULL;否则输入的字符应该赋给root->data,之后依次递归建立它的左子树和右子树?
(1)前序(根)遍历
以上二叉树遍历顺序:ABDGCEF
若二叉树为空,则空操作返回;否则:
1.访问根节点;
2.前序遍历根节点的左子树;
3.前序遍历根节点的右子树;
递归算法:
void PreOrder(binarytree* bt){
if(bt==NULL)//递归调用的出口
return;
else{
visit(bt->data);//访问根节点bt的数据域
PreOrder(bt->Lchild);//前序递归遍历bt的左子树
PreOrder(bt->rchild);//前序递归遍历bt的右子树
}
}(2)中序(根)遍历
以上二叉树遍历顺序:DGBAECF
若二叉树为空,则空操作返回;否则:?
1.前序遍历根节点的左子树
2.访问根节点;
3.前序遍历根节点的右子树
递归算法:
void MidOrder(binarytree* bt){
if(bt==NULL)//递归调用的出口
return;
else{
MidOrder(bt->Lchild);//前序递归遍历bt的左子树
visit(bt->data);//访问根节点bt的数据域
MidOrder(bt->rchild);//前序递归遍历bt的右子树
}
}(3)后序(根)遍历
以上二叉树遍历顺序:GDBEFCA
若二叉树为空,则空操作返回;否则:?
1.前序遍历根节点的左子树;
2.前序遍历根节点的右子树;
3.访问根节点;前序遍历根节点的右子树
递归算法:
void PostOrder(binarytree* bt){
if(bt==NULL)//递归调用的出口
return;
else{
PostOrder(bt->Lchild);//前序递归遍历bt的左子树
PostOrder(bt->rchild);//前序递归遍历bt的右子树
visit(bt->data);//访问根节点bt的数据域
}
}(4)层序遍历
以上二叉树遍历顺序:ABCDEFG
?层序遍历这里使用了前面队列的知识,根据根指针,左孩子,右孩子的顺序逐个入队出队
1.根指针入队
2.根指针出队,根指针有左孩子则左孩子入队;否则,右孩子入队
3.队首出队,队首有左孩子则左孩子入队;否则,右孩子入队
4.循环直至队列为空
递归算法:
void LeverOrder(binarytree* root,LinkQueue *Q){
QElemType q;//q的数据结构类型是最上面二叉树链表的结构体
if(root==NULL)
return;
EnQueue(Q,root);//根指针入队
while(QueueEmpty(*Q)!=1){//当队列非空时
q=DeQueue(Q);//出队
visit(q->data);
if(q->Lchild!=NULL)
EnQueue(Q,q->Lchild);//左孩子入队
if(q->rchild!=NULL)
EnQueue(Q,q->rchild);//右孩子入队
}
}完整代码
1.二叉树.h(保存所有的遍历操作函数)
#include "链队列.h"//链队列是层序遍历的时候要用的,里面还有二叉树结构体的定义
BiNode *Creat(char *str, int *i, int len) { //树的创建
struct BiNode *bt = NULL;
char ch = str[(*i)++];
if (ch == '#' || *i >= len) {
bt = NULL;
} else {
bt = (struct BiNode *)malloc(sizeof(BiNode));
if (bt != NULL) {
bt->data = ch;
bt->Lchild = Creat(str, i, len); //这里的递归要赋值,这样才能建立不同域中的连接关系
bt->rchild = Creat(str, i, len);
}
}
return bt;//返回的一直是根结点
}
void visit(Datatype e) {
printf("%c ", e);
}
void PreOrder(BiNode *bt) { //树的前序遍历
if (bt == NULL) //递归调用的出口
return;
else {
visit(bt->data);//访问根节点bt的数据域
PreOrder(bt->Lchild);//前序递归遍历bt的左子树
PreOrder(bt->rchild);//前序递归遍历bt的右子树
}
}
void MidOrder(BiNode *bt) { //树的中序遍历
if (bt == NULL) //递归调用的出口
return;
else {
MidOrder(bt->Lchild);//前序递归遍历bt的左子树
visit(bt->data);//访问根节点bt的数据域
MidOrder(bt->rchild);//前序递归遍历bt的右子树
}
}
void PostOrder(BiNode *bt) { //树的后序遍历
if (bt == NULL) //递归调用的出口
return;
else {
PostOrder(bt->Lchild);//前序递归遍历bt的左子树
PostOrder(bt->rchild);//前序递归遍历bt的右子树
visit(bt->data);//访问根节点bt的数据域
}
}
void LeverOrder(BiNode *root, LinkQueue *Q) { //树的层序遍历
QElemType q;//q的数据结构类型是最上面二叉树链表的结构体
if (root == NULL)
return;
EnQueue(Q, *root); //根指针入队
while (QueueEmpty(*Q) != 1) { //当队列非空时
q = DeQueue(Q); //出队
visit(q.data);
if (q.Lchild != NULL)
EnQueue(Q, *q.Lchild); //左孩子入队
if (q.rchild != NULL)
EnQueue(Q, *q.rchild); //右孩子入队
}
}
void Bitreedel(BiNode *bt) { //后序删除结点
if (bt == NULL)
return;
else {
Bitreedel(bt->Lchild);//前序递归遍历bt的左子树
Bitreedel(bt->rchild);//前序递归遍历bt的右子树
printf("删除结点:%c ", bt->data); //访问根节点bt的数据域
}
}2.链队列.h(在层序遍历的时候需要调用,里面还有二叉树结构体的定义)(里面有些函数没用到)
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
typedef char Datatype;
typedef struct BiNode {
Datatype data;//数据内容
struct BiNode *Lchild;//指向左孩子结点
struct BiNode *rchild;//指向右孩子结点
} BiNode ;
typedef BiNode QElemType;
//定义队列结点类型
typedef struct QNode {
QElemType data;
struct QNode *next;
} QNode, *QueuePtr;
typedef struct {
QueuePtr front;//头指针
QueuePtr rear;//尾指针
} LinkQueue;
int InitQueue(LinkQueue *Q) {
QueuePtr node;
node = (QueuePtr)malloc(sizeof(QNode));
if (node != NULL) {
node->next = NULL; //创建头指针
Q->front = Q->rear = node;
return 1;
} else
return 0;
}
void DestroyQueue(LinkQueue *Q) {
QueuePtr temp;
while (Q->front != Q->rear) {
temp = Q->front->next;
free(Q->front);
Q->front = temp;
}
free(Q->rear);
}
void ClearQueue(LinkQueue *Q) { //保留队列头指针和队列尾指针,其他结点销毁
QueuePtr p, q;
Q->rear = Q->front; //将尾指针归位到头指针
Q->front->next = NULL;//天哪一定要记得把头节点next域设为NULL,不然还是被释放了的q,就乱指了
q = Q->front->next; //队列头
while (q != NULL) {
p = q->next;
free(q);
q = p;
}
}
int QueueEmpty(LinkQueue Q) { //是否为空,为空返回,非空返回0
if (Q.front->next == NULL)
return 1;
else
return 0;
}
int QueueLength(LinkQueue Q) { //返回队列长度
QueuePtr p = Q.front->next;
if (p == NULL) {//刚初始化完的队列长度为0
return 0;
}
int count = 1;
while (p != Q.rear) {
count++;
p = p->next;
}
return count;
}
QElemType GetHead(LinkQueue Q) { //若队列非空,返回队列首的值
if (QueueEmpty(Q) != 1)
return Q.front->next->data;
else
printf("队列为空!\n");
}
void EnQueue(LinkQueue *Q, QElemType e) { //将e元素插入队列
QueuePtr node;
node = (QueuePtr)malloc(sizeof(QNode));
if (node != NULL) {
node->next = NULL;
node->data = e;
Q->rear->next = node;
Q->rear = node;
} else
printf("EnQueue error!\n");
}
QElemType DeQueue(LinkQueue *Q) { //删除队头元素,并返回其值
QElemType e;
QueuePtr q;
if (QueueEmpty(*Q) != 1) {
q = Q->front->next;
e = Q->front->next->data;
Q->front->next = q->next;
if (Q->rear == q)//队头等于队尾,防止尾指针丢失
Q->rear = Q->front;
free(q);
return e;
} else
printf("队列为空!\n");
}
void QueueTraverse(LinkQueue Q) { //从队列头到尾遍历队列元素并输出
QueuePtr p = Q.front->next;
// printf("从队列头到尾遍历队列元素并输出:\n");
if (QueueEmpty(Q) == 1) {
printf("队列为空!\n");
return;
}
while (p != NULL) {
if (p != Q.rear)
printf("%c ", p->data);
else
printf("%c\n", p->data);
p = p->next;
}
}2.二叉树测试.c (测试上述功能)
#include "二叉树.h"
main() {
printf("测试建立一个二叉树\n");
BiNode *bt;
int i = 0, len;
char str[50];
printf("输入一个字符串用于建立二叉树:");
scanf("%s", str);
len = strlen(str);
bt = Creat(str, &i, len);
printf("测试遍历操作:\n");
printf("测试树的前序遍历:");
PreOrder(bt);
printf("\n");
printf("测试树的中序遍历:");
MidOrder(bt);
printf("\n");
printf("测试树的后序遍历:");
PostOrder(bt);
printf("\n");
printf("测试树的层序遍历:");
LinkQueue Q;
InitQueue(&Q);
LeverOrder(bt, &Q);
printf("\n");
//测试按照后序逐个删除结点
Bitreedel(bt);
}测试输出:

?初学小白,有错误欢迎指正喔!~