[数据结构与算法]【2022国赛模拟】相似序列问题——DFA（DP套DP）

因为找不到原题，所以这个链接纯粹占空间的

题目描述

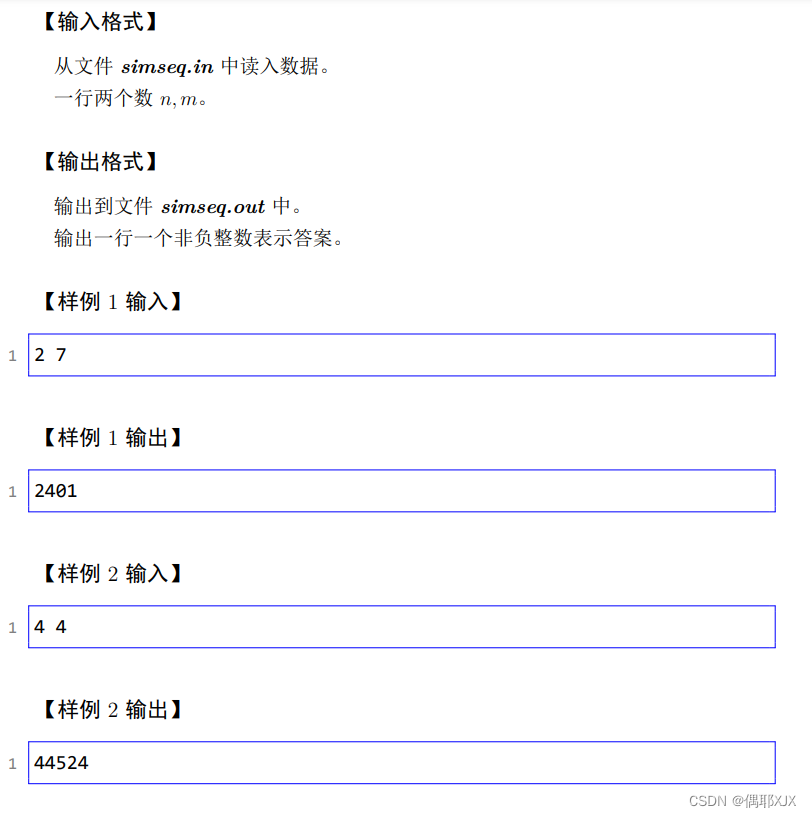
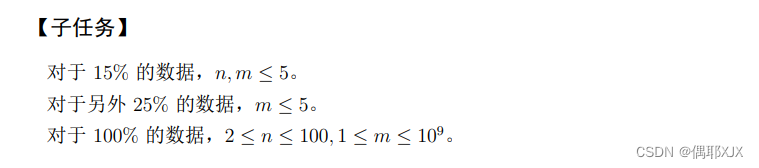
注意这个序列对是有序的，也就是说当序列 $A,B$ 不同时，序列对 $(A,B)$ 和 $(B,A)$ 是不同的。

题解

首先考虑怎么判断两个长度为 $n$ 的序列 $A,B$ 相似。

我们可以用一个简单的记录 bool 值的 DP。考虑从左往右每次加入同一位置的 $A,B$ 序列上的数，记 $dp[i][j][k]$ 表示考虑两序列的前 $i$ 个元素，$A$ 序列删了 $j$ 个元素，$B$ 序列删了 $k$ 个元素，它们剩下部分是否能够匹配。特别地，当 $j,k$ 一个为1一个为2的时候，你不能确定删1的那边的最后一个元素是哪个，所以需要额外记录一下删的是否是最后一个。

容易发现对于每个 $i$ 来说，DP 的状态非常少，转移最多也只需要两个序列 $i?1,i?2$ 处的信息。我们可以建出这个 DP 的 DFA，然后减少一下状态，就可以直接在 DFA 上计数了。

容易发现 DP 的状态数最多有11个，所以对于每种 $i?1,i?2$ 处的元素取值情况，共需要建立 $2^{11}$ 个节点。虽然元素的取值情况貌似最多有 $m^4$ 种，但是我们转移的时候只关心这4个值之间的不等关系，所以有用的状态数就等于4个元素的最小表示的数量，最多15种。

设 DFA 的节点数为 $k(k\le 15\times 2^{11})$，每个节点的出边数量是常数条，所以算法总时间为 $O(nk)$。

代码

代码虽然不长，但需要非常细致的讨论。

#include<bits/stdc++.h>//JZM yyds!!
#define ll long long
#define lll __int128
#define uns unsigned
#define fi first
#define se second
#define IF (it->fi)
#define IS (it->se)
#define END putchar('\n')
#define lowbit(x) ((x)&-(x))
#define inline jzmyyds
using namespace std;
const int MAXN=114514;
const ll INF=1e17;
ll read(){
	ll x=0;bool f=1;char s=getchar();
	while((s<'0'||s>'9')&&s>0){if(s=='-')f^=1;s=getchar();}
	while(s>='0'&&s<='9')x=(x<<1)+(x<<3)+(s^48),s=getchar();
	return f?x:-x;
}
int ptf[50],lpt;
void print(ll x,char c='\n'){
	if(x<0)putchar('-'),x=-x;
	ptf[lpt=1]=x%10;
	while(x>9)x/=10,ptf[++lpt]=x%10;
	while(lpt>0)putchar(ptf[lpt--]^48);
	if(c>0)putchar(c);
}
const ll MOD=1e9+7;
using pii=pair<int,int>;
vector<pii>G[MAXN];
int n,k,g[233],h[233];
ll m,dp[2][MAXN],ans;
int suo(int o,int a,int b,int c){
	int e=0,u=(a==o?0:++e),v=(b==o?0:b==a?u:++e),w=(c==o?0:c==a?u:c==b?v:++e);
	return (u<<4)|(v<<2)|w;
}
/*
00 0
01 1
02 2
10 3
11 4
12 5
12- 6
20 7
21 8
21- 9
22 10
*/
int main()
{
	freopen("simseq.in","r",stdin);
	freopen("simseq.out","w",stdout);
	for(int a=0;a<=1;a++)
		for(int b=0;b<=a+1;b++)
			for(int c=0;c<=max(a,b)+1;c++)
				g[(a<<4)|(b<<2)|c]=k,h[k++]=(a<<4)|(b<<2)|c;
	n=read(),m=read();
	for(int id=0;id<k;id++){
		int o=h[id],a=o>>4,b=(o>>2)&3,c=o&3,e=max({a,b,c});
		for(int s=0;s<(1<<11);s++){
			for(int u=0;u<=e+1;u++)
				for(int v=0;v<=max(e,u)+1;v++){
					ll cg=1;
					if(u>e){
						(cg*=m-e-1+MOD)%=MOD;
						if(v>u)(cg*=m-u-1+MOD)%=MOD;
					}else if(v>e)(cg*=m-e-1+MOD)%=MOD;
					int t=0,di=g[suo(a,u,c,v)];
					// 0au
					// bcv
					if(((s>>0)&1)){
						if(u==v)t|=1<<0;
						t|=1<<1,t|=1<<3,t|=1<<4;
					}if(((s>>1)&1)){
						if(a==v)t|=1<<1,t|=1<<4;
						t|=1<<2,t|=1<<6;
					}if(((s>>2)&1)){
						if(!v)t|=1<<2,t|=1<<6;
					}if(((s>>3)&1)){
						if(u==c)t|=1<<3,t|=1<<4;
						t|=1<<7,t|=1<<9;
					}if(((s>>4)&1)){
						if(u==v)t|=1<<4;
						t|=1<<5,t|=1<<8,t|=1<<10;
					}if(((s>>5)&1)){
						if(a==v)t|=1<<5,t|=1<<10;
					}if(((s>>6)&1)){
						if(!v)t|=1<<5,t|=1<<10;
					}if(((s>>7)&1)){
						if(u==b)t|=1<<7,t|=1<<9;
					}if(((s>>8)&1)){
						if(u==c)t|=1<<8,t|=1<<10;
					}if(((s>>9)&1)){
						if(u==b)t|=1<<8,t|=1<<10;
					}if(((s>>10)&1)){
						if(u==v)t|=1<<10;
					}G[id<<11|s].emplace_back(cg,di<<11|t);
				}
		}
	}
	dp[0][1]=1;
	for(int i=1;i<=n;i++){
		bool e=i&1,t=e^1;
		for(int j=0;j<(k<<11);j++)dp[e][j]=0;
		for(int s=0;s<(k<<11);s++)if(const ll d=dp[t][s])
			for(auto&x:G[s])(dp[e][x.se]+=x.fi*d)%=MOD;
	}
	for(int s=0;s<(k<<11);s++)if(const int d=dp[n&1][s])
		if((s&1)||((s>>4)&1)||((s>>10)&1)){
			ans+=d;
			if(ans>=MOD)ans-=MOD;
		}
	print(ans);
	return 0;
}