基本概念
-
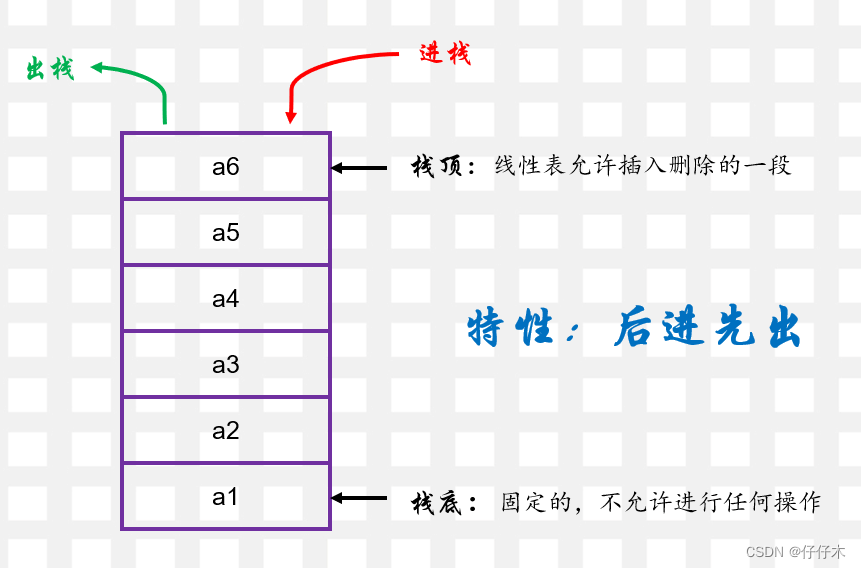
栈的定义
栈是一种受限的线性表,只能在某一段进行插入或者删除操作
-
求出栈个数:
n个不同元素进栈,出栈元素不同排列个数为: 1 n + 1 C 2 n n \frac{1}{n+1}C^n_{2n} n+11?C2nn?
??
例: n=3的时候,个数为: 1 3 + 1 C 2 ? 3 3 = 5 \frac{1}{3+1}C^3_{2*3}=5 3+11?C2?33?=5
??
?分别为:123、132、213、231、321 -
基本操作
void InitStack(SqStack &S) //初始化栈 bool StackEmpty(SqStack S) //判断空栈 bool Push(SqStack &S,ElemType e) //进栈 bool Pop(SqStack &S,ElemType &e) //出栈 bool GetTop(SqStack S,ElemType &e) //读栈顶元素 void DestoryStack(SqStack &S) //销毁栈
栈的顺序存储(顺序栈)
初始化top=-1的情况
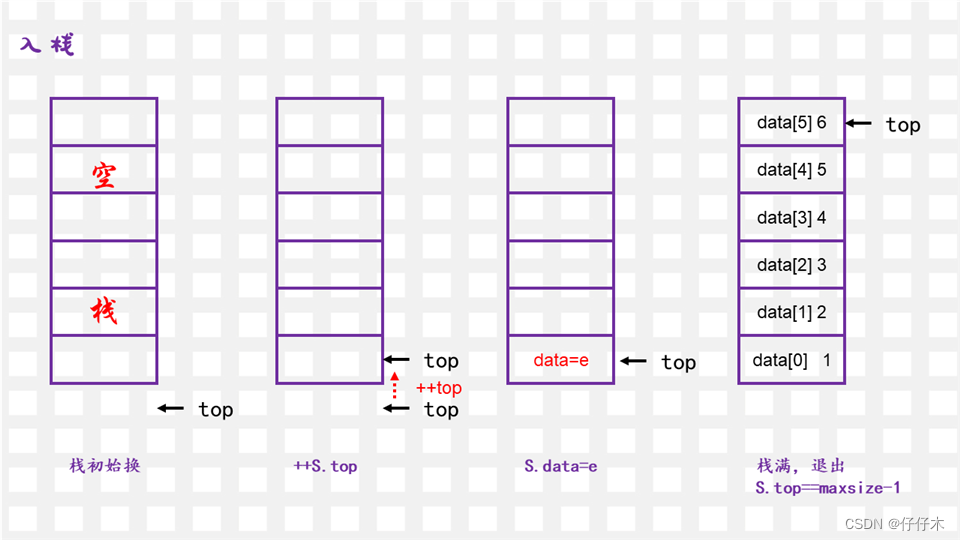
进栈
-
图解
-
代码
bool Push(SqStack &S,ElemType e){ if (S.top==MaxSize-1) return false; S.data[++S.top]=e; return true; }
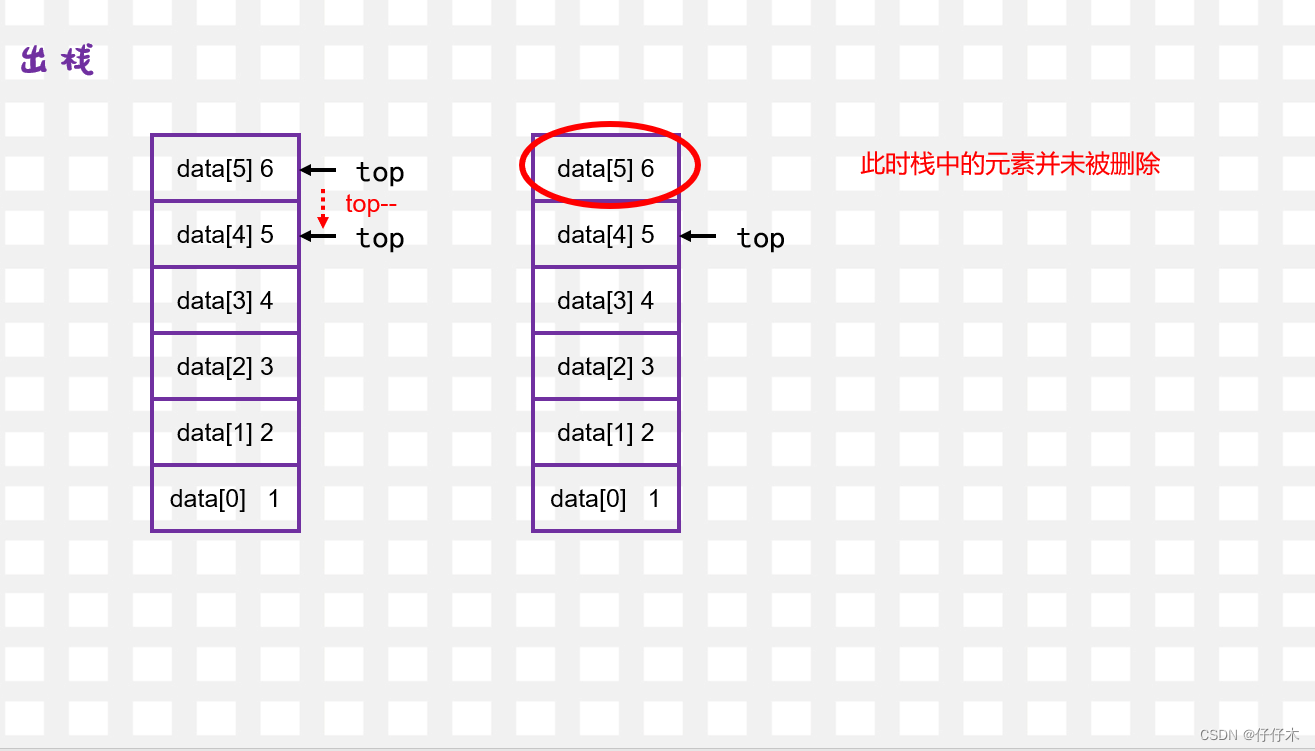
出栈
-
图解
-
代码
bool Pop(SqStack &S,ElemType &e){ if (S.top==-1) return false; e=S.data[S.top--]; return true; }
完整代码
/*
*Function:顺序栈
*/
#include "stdio.h"
#include "stdlib.h"
#define MaxSize 50
typedef int ElemType;
typedef struct {
ElemType data[MaxSize]; //存放栈中元素
int top; //栈顶指针
}SqStack;
/*初始化空栈*/
void InitStack(SqStack &S){
S.top=-1;
}
/*空栈判断*/
bool StackEmpty(SqStack S){
if (S.top==-1)
return true;
else
return false;
}
/*进栈*/
bool Push(SqStack &S,ElemType e){
if (S.top==MaxSize-1)
return false;
S.data[++S.top]=e;
return true;
}
/*出栈*/
bool Pop(SqStack &S,ElemType &e){
if (S.top==-1)
return false;
e=S.data[S.top--];
return true;
}
/*读栈(栈顶)*/
bool GetTop(SqStack S,ElemType &e){
if (S.top==-1)return false;
e=S.data[S.top];
return true;
}
/*销栈*/
void DestoryStack(SqStack &S){
S.top=-1;
}
/*便利*/
void Proint(SqStack S){
int i=0;
while(i<=S.top){
printf("%d ",S.data[i++]);
}
printf("\n");
}
int main(){
SqStack S;
printf("***************************************\n");
printf("******** 1.初始化栈 2.空栈判断 ********\n");
printf("******** 3. 进 栈 4. 出 栈 ********\n");
printf("******** 5.读取栈顶 6. 销 栈 ********\n");
printf("******** 7. 遍 历 0. 退 出 ********\n");
printf("***************************************\n");
bool flag= true;
int x;
ElemType e;
while(flag){
printf("请输入命令:");
scanf("%d",&x);
switch (x) {
case 1:
InitStack(S);
printf("\t空栈初始化完成\n");
break;
case 2:
if(StackEmpty(S)) printf("\t该栈是空栈\n");
else printf("\t该栈不是空栈\n");
break;
case 3:
printf("\t请输入要进栈的元素:");
int a;
scanf("%d",&a);
if(Push(S,a))printf("\t元素进栈成功\n");
else printf("\t元素进栈失败\n");
break;
case 4:
if(Pop(S,e))
printf("\t元素出栈成功,出栈的元素为:%d\n",e);
else
printf("\t元素进栈失败\n");
break;
case 5:
if(GetTop(S,e))
printf("\t栈顶元素为:%d\n",e);
else
printf("\t该栈为空栈\n");
break;
case 6:
DestoryStack(S);
printf("\t销毁成功\n");
break;
case 7:
printf("\t当前栈中元素:");
Proint(S);
break;
case 0:
printf("退出成功\n");
flag= false;
break;
default:
printf("命令错误,请重新输入!!!");
break;
}
}
}
运行截图

初始化top=0的情况
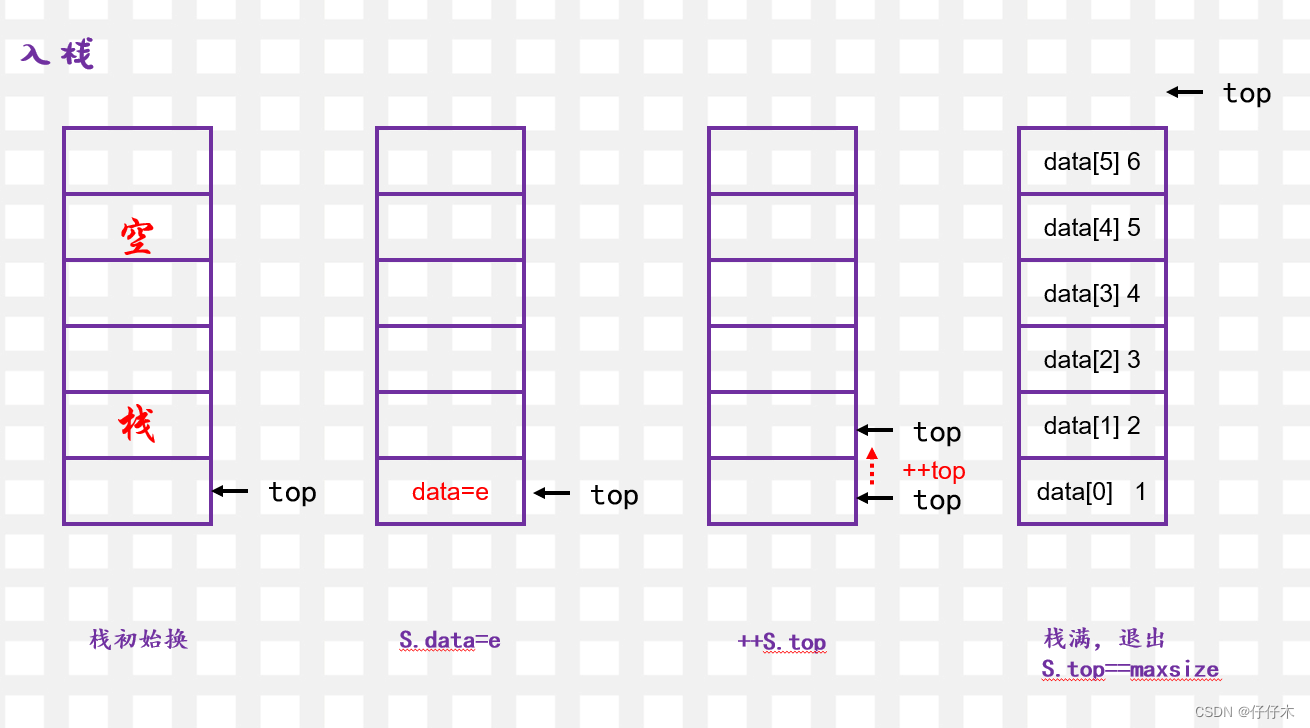
- 初始化栈:
S.top=0 - 入栈:
S.data[S.top++]=e - 出栈:
e=S.data[--S.top] - 栈满:
S.top==Maxsize
完整的代码可以根据上面的完整代码进行更改