连通分量:任意两点可以相互到达。(注:任何一个点本身就是强连通的)
强连通分量:极大连通分量,加上任意一个点之后就不是连通分量了
有向无环图(DAG):也就是拓扑图。
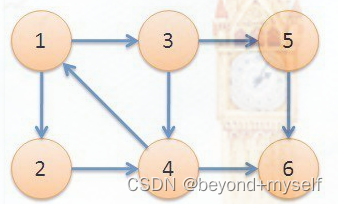
dfs序:按照dfs的顺序为每个点编号
树枝边:(x,y),x是y的父节点
前向边:(x,y),x是y的祖先节点
后向边:(x,y),y是x的祖先节点
横叉边:(x,y),其中一个是已经搜过的
一般是左边,右边的不叫横叉边
判断某一个点是否在强连通分量中:
①:是不是可以回到祖先节点,即存在一条后向边指向祖先节点
②:先走到一个横叉边,然后再走到祖先节点
Tarjan算法求强连通分量:
时间戳:通过dfs给每个点设置一个编号。
对每个点定义两个时间戳:
dfn[u]表示遍历到u的时间
low[u]表示从u开始走,所能遍历到的最小的时间戳。
如果u是所在强连通分量的最高点,则dfn[u]=low[u]
tarjan算法:遇到dfn[u]==low[u]的就是强连通分量,这个意思就是他能够到达的最小的点是它本身的时候那么就是强连通分量。因为强连通分量,它必然是每两个点之间都可以互相到达。所以必然会形成一个环,因为我们在dfs的时候一定是从上到下的也就是时间戳也是从小到大的,所以我们认为这个环上最小的点为关键点。因为在具体遍历过程中一定是每一点遍历完成后才会判断是不是符合强连通变量,这样判断的时候不能到达这个变量的已经出栈,能够到达的还在栈里面,且是最大的(这个点已经遍历完成了)。这样就把包括本身的所有点出栈,形成了一个强连通分量。
缩点:因为连通分量之间都是可以互相到达的,也就是通过外面的点到达这个连通分量后一定可以到达连通分量里的任意一个点,所以可以将此连通分量缩点,缩完点后整个图就会称为一个有向无环图。
tarjan算法代码模板:
void tarjan(int u)
{
dfn[u]=low[u]=++timestamp;
stk[++top]=u,in_stk[u]=true;
for(int i=h[u];~i;i=ne[i])
{
int j=e[i];
if(!dfn[j])
{
tarjan(j);
low[u]=min(low[u],low[j]);
}
else if(in_stk[j]) low[u]=min(low[u],dfn[j]);
}
if(dfn[u]==low[u])
{
++scc_cnt;//连通分量数加1
int y;
do
{
y=stk[top--];
in_stk[y]=false;
id[y]=scc_cnt;//y在此连通分量里
Size[scc_cnt]++;
}while(y!=u);
}
}
缩点模板:
for(int i=1;i<=n;i++)
{
for(int j=h[i];~j;j=ne[j])
{
int k=e[j];
int a=id[i],b=id[k];
if(a!=b) dout[a]++;//a的出度加1,也就是本来他来是连着的,但是求连通分量之后就不连了,应该把他们连接起来
}
}
题目链接
kosaraju算法(两次dfs):正向可以到达,反向还可以到达的就是强连通分量,这里注意的就是那个第一次dfs入栈的顺序是按照遍历完的顺序入栈的,所以第一个遍历的一定是最后一个入栈,所以节点进入到栈中完全后,从栈顶到栈底其实就是按照dfs序的顺序执行的。
算法模板:
void dfs1(int u)
{
st[u] = true;
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if (!st[j])
dfs1(j);
}
stk[ ++ top] = u;
}
void dfs2(int u)
{
id[u] = scc_cnt;
sz[scc_cnt] ++ ;
st[u] = true;
for (int i = hs[u]; ~i; i = ne[i])
{
int j = e[i];
if (!st[j])
dfs2(j);
}
}
下面是一道例题:
题目链接