一、基本思想
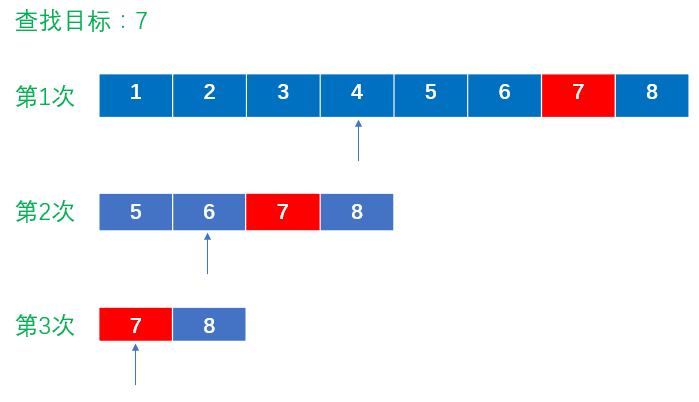
假设表中元素是按升序排列,将表中间位置记录的关键字与查找关键字比较,如果两者相等,则查找成功;否则利用中间位置记录将表分成前、后两个子表,如果中间位置记录的关键字大于查找关键字,则进一步查找前一子表,否则进一步查找后一子表。
重复以上过程,直到找到满足条件的记录,此时查找成功;或直到子表不存在为止,此时查找不成功。
二、时间复杂度
二分查找的基本思想是将n个元素分成大致相等的两部分,取a[n/2]与x做比较,
如果x=a[n/2],则找到x,算法中止;
如果x<a[n/2],则只要在数组a的左半部分继续搜索x,
如果x>a[n/2],则只要在数组a的右半部搜索x。
时间复杂度就是求while循环的次数。
假设总共有n个元素,每次查找的区间大小就是n,n/2,n/4,…,n/2^k,
其中k就是循环的次数。
由于n/2^k取整后>=1,令n/2^k=1, 可得k=log2(n),(以2为底n的对数)。?
所以时间复杂度可以表示为O(h)=O(log2(n))
三、优缺点
优点是比较次数少,查找速度快,平均性能好;
缺点是要求待查表为有序表,且插入删除困难。
因此,折半查找方法适用于不经常变动而查找频繁的有序列表。?
?四、C++实现
#include<iostream>
using namespace std;
// 递归实现
int recur_bin_search(int a[], int low, int high, int key)
{
if(low > high)
return -1;
int mid = (low + high) / 2;
if(key == a[mid])
return mid;
else if(key < a[mid])
return recur_bin_search(a, low, mid - 1, key);
else
return recur_bin_search(a, mid + 1, high, key);
}
// 非递归实现
int bin_search(int a[], int n, int key)
{
int low ,high, mid;
low = 0;
high = n - 1;
while(low <= high)
{
mid = (low + high) / 2; // 向下取整
if(key == a[mid])
return mid;
else if(a[mid] < key)
low = mid + 1;
else
high = mid - 1;
}
return -1;
}
// 非递归实现,向下取整,等价于bin_search函数
int bin_search_1(int a[], int n, int key)
{
int mid, low = 0, high = n - 1; //闭区间[0, n - 1]
while (low < high)
{
mid = low + ((high - low) >> 1); //向下取整
if (a[mid] < key)
low = mid + 1;
else
high = mid;
}
if (a[high] == key)
return high;
return -1;
}
// 非递归实现,向上取整
int bin_search_2(int a[], int n, int key)
{
int mid, low = 0, high = n - 1;//闭区间[0, n - 1]
while (low < high)
{
mid = low + ((high + 1 - low) >> 1);//加1是向上取整
if (a[mid] <= key)
low = mid;
else
high = mid - 1;
}
if (a[low] == key)
return low;
return -1;
}
int main()
{
int a[] = {10, 20, 30, 40, 50, 60, 60, 70};
int num = 60;
int cnt = sizeof(a) / sizeof(int);
cout << recur_bin_search(a, 0, cnt, num) << endl;
cout << bin_search_1(a, cnt, num) << endl;
cout << bin_search_1(a, cnt, num) << endl;
cout << bin_search_2(a, cnt, num) << endl;
return 0;
}
运行结果:
6
5
5
6五、分析
(一)为何需要向下取整或向上取整呢?
当数组里的元素数量为奇数时,中间那个元素是固定的。
当数组里的元素数量为偶数时,中间有两个元素,向下取整就是取左边的那个数,向上取整就是取右边的那个数。
比如 a[] = {1, 2, 3, 4, 5, 6},3和4都是中间元素,向下取整得到的是3,向上取整得到的是4。
?
(二)while里要不要加等号
1、对于bin_search函数,等号是一定要加的
??? 例1:
??? a[] = {10, 20, 30, 40, 50, 60}, key = 20,low = 0, high = 5,
??? 第一次循环, mid = (0 + 5) / 2 = 2, a[mid] > key, high = mid - 1 = 1
??? 第二次循环,mid = (0 + 1) / 2 = 0, a[mid] < key, low = mid + 1 = 1
??? 假如没有等号,即while(low < high),那么就不能再循环了,得不到正确的结果。
??? 加了等号之后,即while(low <= high),
??? 第三次循环,mid = (1 + 1) / 2 = 1,a[mid] = key,返回下标1。程序结束。
2、对于bin_search_1与bin_search_2函数,等号是一定不能加的
??? 以bin_search_1为例,一旦加了等号之后,执行到low = high时, mid = low + (high - low) >> 1 = low
??? 执行else语句,high = mid = low,陷入死循环。
3、bin_search_2与bin_search_1道理一样,不能加等号
(三)bin_search_1与bin_search_2在while结束后,为何还要用if再判断一次?
以bin_search_1为例,while循环结束后,有两种情况:要么a[high] = a[mid] = key, 要么a[high] = a[mid] > key。所以还要判断a[high]是否与key相等。
例2:
a[ ] = {10, 20, 30, 40, 50, 60}, key = 50,最终high = mid = 4, a[high] = key
例3:
a[ ] = {10, 20, 30, 40, 50, 60}, key = 45,最终high = mid = 4, a[high] > key
bin_search_2同理。
4 为何bin_search_1里,low = mid + 1, high = mid?
因为 a[mid] < key,说明key一定处于[mid + 1]和high之间。
反过来则是 a[mid] >= key。则key一定处于位置 low和mid之间。
bin_search_2中同理。
?
六、二分查找判定树
对表中每个记录的查找过程,可用二叉树来描述,树中的每个结点对应有序表中的一个记录,结点的值为该记录在表中的位置,常将这个描述二分查找过程的二叉树称为二分查找判定树。
1、构造
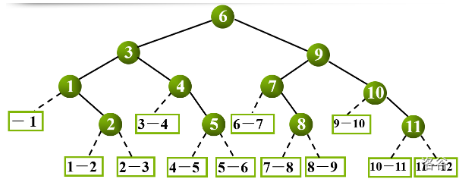
当 n=0 时,折半查找判定树为空
当 n>0 时,折半查找判定树的根结点为 mid=(n+1)/2,根结点的左子树是与有序表 r[1] ~ r[mid-1] 相对应的折半查找判定树,根结点的右子树是与 r[mid+1] ~ r[n] 相对应的折半查找判定树。?
2、性质
任意两棵折半查找判定树,若它们的结点个数相同,则它们的结构完全相同
折半查找的判定树一定是平衡二叉树且只有最下面一层是不满的
具有n个结点的折半查找树的高度为 ![]() log(n+1) 向上取整,或者 (logn) 向下取整+1
log(n+1) 向上取整,或者 (logn) 向下取整+1
任意结点的左右子树中结点个数最多相差 1
任意结点的左右子树的高度最多相差 1
任意两个叶子所处的层次最多相差 1


左子树 < 中间结点 < 右子树结点
属于二叉排序树的定义、并且是平衡二叉排序树
n个成功结点的判定树、失败结点个数是:n+1个
n+1=成功结点的空链域数量
?

?
七、复杂度分析
最坏情况下,关键码比较次数为 log2(n+1),时间复杂度为 O(logn)
在表中查找任一记录的过程,即是折半查找判定树中从根结点到该记录结点的路径,和给定值的比较次数等于该记录结点在树中的层数。
具有 n 个结点的二分查找判定树的深度为![]() ,因此当查找成功时,所进行的关键码比较次数至多为 ?log2?n?+1 (向下取整,小),而查找不成功时,就是走了一条从根结点到外部结点的路径,和给定值进行的关键码的比较次数等于该路径上内部结点的个数,即失败情况下的平均查找长度等于树的高度。
,因此当查找成功时,所进行的关键码比较次数至多为 ?log2?n?+1 (向下取整,小),而查找不成功时,就是走了一条从根结点到外部结点的路径,和给定值进行的关键码的比较次数等于该路径上内部结点的个数,即失败情况下的平均查找长度等于树的高度。
以深度为 k 的满二叉树为例,其深度为:![]() ,
,
树上的第 i 层有:?![]() 个结点,
个结点,
假设表中的每条记录查找概率相等,即:?![]()
则有:
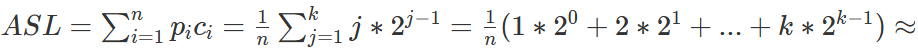
?![]()
故平均时间复杂度为:O(logn)
原文来自