开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 1.数据结构与算法基础知识 -> 正文阅读

[数据结构与算法]1.数据结构与算法基础知识

文章目录

数据结构与算法 (Python 版)

数据结构与算法 (Python 版)

知识点一 : 算法的概念

1.概述:
??1.1 算法 (Algorithm)即一个计算过程, 即用来解决问题的方法.
??
??1.2 著名 IT 科学家尼古拉斯·沃斯 (Niklaus Wirth) 认为 " 程序 = 数据结构 + 算法 "

图片/数据结构与算法1.png

??
??
??

知识点二 : 时间复杂度

1.概述:
??1.1 时间复杂度: 用来评估算法运行效率的一个式子 ( 即用一个类似于公式的东西能够形象的比较两个算法的快慢 )
??
??1.2 为什么不使用时间来体现算法的运行快慢?
????- 电脑本身内存的运行效率有差异.
????- 执行代码的次数有差异.(如for循环1次,10次,100次都有所不同)

2.案例:
??2.1 打印一行代码
????我们将一个print定义为叫O(1),我们将O理解为一个约等号,大约的意思,括号中的东西就类似于单位,1就是一个单位,类似于秒这个单位,但不是1秒,而就是1,它没有后缀.

# 只执行了一次,时间消耗大约为1,即O(1)
print("Hello World")

??
??2.2 打印一个for循环

# i执行n次, 时间消耗大约为 1×n, 即O(n)
for i in range(n):
	print("Hello World")

??
??2.3 打印两个for循环

# i执行1次时,j执行n次 时间消耗大约为 1×n,即O(n)
# 然而i本身还要执行n次,所以是 n×(1×n), 最终的执行时间为 O(n^2)
for i in range(n):
    for j in range(n):
        print("Hello World")

??
??2.4 打印三个for循环

# 同两个for循环,for循环执行n次即时间消耗O(n),三次循环即 n×n×n,故最终的消耗时间为O(n^3)
for i in range(n):
    for j in range(n):
        for k in range(n):
            print("Hello World")

??
??2.5 打印三行代码

# 执行三次,因为执行三次print和执行一次print的的差距几乎忽略不计,时间复杂度 O(1)
# 因为按正常逻辑来说,执行三次print的时间复杂度本来应是3×1 即O(3)
# 但是因为时间复杂度的低精度性,就直接被约算成了O(1)
print("Hello World")	
print("Hello Python")	
print("Hello Algorithm")

注意点1 : 执行基本操作,只要它的问题规模不上升到n这么大的时候,它的时间复杂度就是O(1)
????(就像是我们睡觉只会说大约睡了几个小时,而不是说睡了几个小时几分几秒.)

注意点2 : 时间复杂度是一个低精度的计算方式, 只算一个大致的内容即可.

??
??2.6 打印双重for-print循环

# 同理两次for循环应该是n^2,又因为多打印了n次Hello World
# 正常来说,时间复杂度应该是O(n^2+n)
# 但是同样是因为时间复杂度的低精度性,故而这里的时间复杂度应该是O(n^2)
for i in range(n):
    print("Hello World")
    for j in range(n):
        print("Hello World")

??
??2.7 打印减半while循环

# 当n=64时输出:64,32,16,8,4,2
# 代码每执行一次,n的值都比之前少一半
# 2^6 = 64 → 1og~2~64 = 6
# 所以将时间复杂度记为O(log~2~n) 或 O(logn)
# 循环减半logn
while n > 1:
    print(n)
    n = n // 2

??
3.总结:
??3.1 时间复杂度是用来估计算法运行时间的一个式子 (单位).
??
??3.2 一般来说 (即在基本上相同条件下), 时间复杂度高的算法比复杂度低的算法慢.
??
??3.3 常见的时间复杂度 (按效率排序):
????O(1) < O(logn) < O(n) < O(nlogn) < O(n²) < O(n²logn) < O(n3 )
??
??3.4 复杂问题的时间复杂度:
????O(n!)?O(2ⁿ)?O(nⁿ) …
??
??3.5 快速判断算法复杂度 (适用于绝大多数简单情况,复杂情况需要根据算法执行过程判断):
????- 确定问题规模 n → 如列表排序,需要先确定列表的长度
????- 循环减半过程 → logn
????- k 层关于 n 的循环 → n^k (几层循环就是n的几次方)

??
??
??

知识点三 : 空间复杂度

1.概述:
??1.1 空间复杂度: 用来评估算法内存占用大小的式子
????(小电影100MB能看就不要去下300MB的看，代码同理，能用10MB解决的问题就不要用30MB存储去多占用空间.)
图片/数据结构与算法2.png

??
??1.2 空间复杂度表示:
????- 算法使用了几个变量: O(1)
????- 算法使用了长度为 n 的一维列表: O(n)
????- 算法使用了 m 行 n 列的二维列表: O(mn)
???? (空间复杂度一般来说有O(1)、O(n)、O(n²)、O(logn)、O(NlogN)几种.但是其实最常用的也就是O(1) 或者 O(n)，用到O(n²)的情况都不多)
??
??1.3 空间换时间:
????在我们写算法时，时间复杂度和空间复杂度只能二选一进行优化，但最好是优化时间复杂度，毕竟在这个学习资料都要放3个T的时代，存储空间并不算昂贵，但是时间真的很宝贵。故而优化时:时间复杂度>空间复杂度.

??
??
??

知识点四 : 递归

1.概述:
??1.1 递归的两个特点:
????- 调用自身
????- 结束条件
??
2.实例:
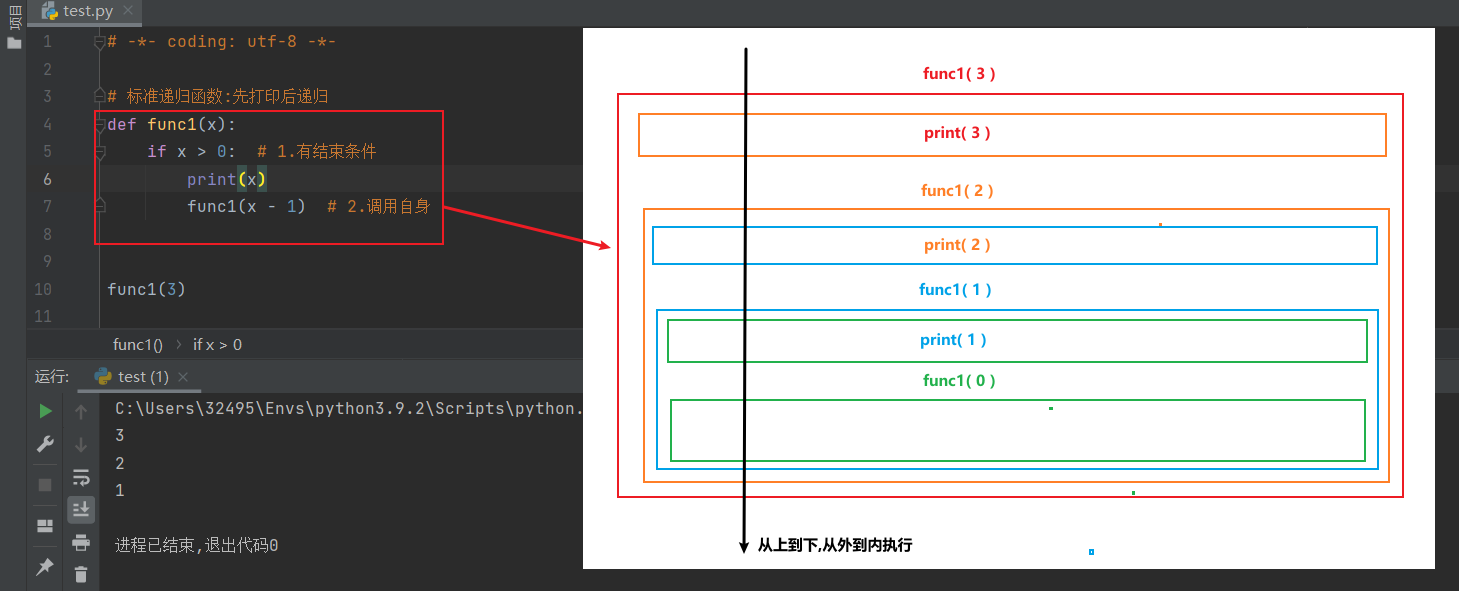
??2.1 先打印后递归

# 标准递归函数:先打印后递归
def func1(x):
    if x > 0:	# 1.有结束条件
        print(x)
        func1(x-1)	# 2.调用自身

        
func1(3)

图片/数据结构与算法3.png

??
??2.2 先递归后打印

# 标准递归函数: 先递归后打印
def func2(x):
    if x > 0:	# 1.有结束条件
        func2(x-1)	# 2.调用自身
        print(x)
  

func2(3)

图片/数据结构与算法4.png

??
??
??

知识点五 : 递归算法:汉诺塔问题

1.题目

??原版: 汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞n片黄金圆盘。大梵天命令婆罗门把圆盘从下自上开始、按大小顺序重新摆放在另一根柱子上。并且规定，小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘，如图所示。问应该怎样移动，才能将圆盘移动到另一根柱子上。
??
??数学版: 从左到右有A、B、C三根柱子，其中A柱子上面有从小叠到大的n个圆盘，现要求将A柱子上的圆盘移到C柱子上去，期间只有一个原则：一次只能移到一个盘子且大盘子不能在小盘子上面，求移动的步骤和移动的次数。

??
??

2.思路

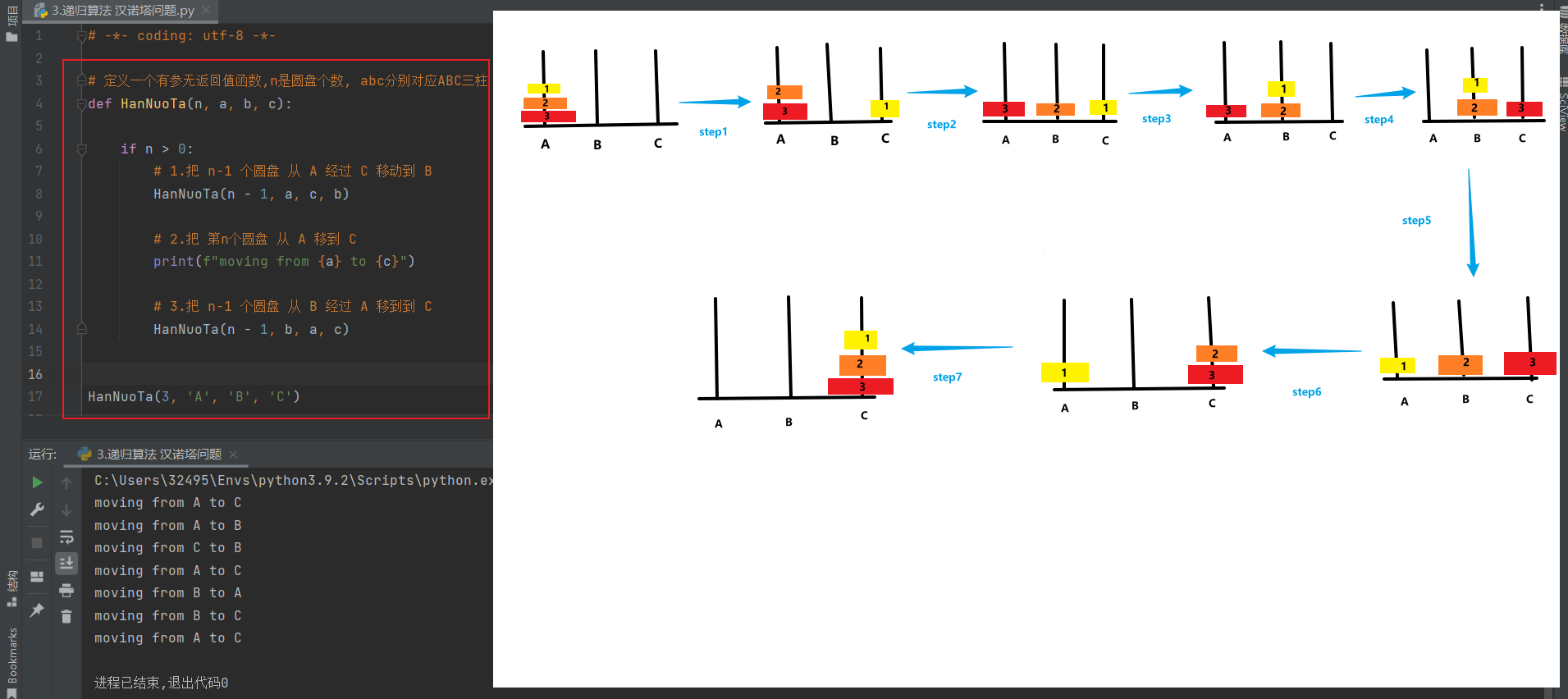
(1) 假设 n = 2 时:
??第一步: 把圆盘1 从 A 移动到 B
??第二步: 把圆盘2 从 A 移动到 C
??第三步: 把圆盘1 从 B 移动到 C

图片/数据结构与算法5.png

??
??
(2) 假设有n个盘子时:
??第一步: 把 n-1 个圆盘从 A 经过 C 移动到 B
??第二步: 把第n个圆盘从 A 移到 C
??第三步: 把 n-1 个圆盘从 B 经过 A 移到到 C

图片/数据结构与算法6.png

??
??

3.代码

# -*- coding: utf-8 -*-

# 定义一个有参无返回值函数,n是圆盘个数, abc分别对应ABC三柱
def HanNuoTa(n, a, b, c):

    if n > 0:
        # 1.把 n-1 个圆盘 从 A 经过 C 移动到 B
        HanNuoTa(n - 1, a, c, b)

        # 2.把 第n个圆盘 从 A 移到 C
        print(f"moving from {a} to {c}")

        # 3.把 n-1 个圆盘 从 B 经过 A 移到到 C
        HanNuoTa(n - 1, b, a, c)


HanNuoTa(3, 'A', 'B', 'C')

图片/数据结构与算法7.png

??
??

4.小结

汉诺塔移动次数的递推式: h(x) = 2h(x-1) + 1
- h (64) =18446744073709551615
- 假设婆罗门每秒钟搬一个盘子,则总计需要5800亿年

??
??
??

知识点六 : 查找

查找 : 在一些数据元素中, 通过一定的方法找出与给定关键字相同的数据元素的过程.
列表查找 ( 线性表查找 ) : 从列表中查找指定元素
- 输入 : 列表、待查找元素
- 输出 : 元素下标 ( 未找到元素时一般返回None或-1 )
内置列表查找函数 : index( )

??
??
??

1.顺序查找

顺序查找 ( Linear Search ) : 也称线性查找, 从列表第一个元素开始顺序进行搜索, 直到找到元素或搜索到列表最后一个元素为止.
顺序查找时间复杂度 : O(n)

# -*- coding: utf-8 -*-

def linear_search(li, val):

    # enumerate(teration, start): 枚举函数, 默认包含两个参数.
    #   1.iteration参数:需要遍历的参数 (如字典、列表、元组等)
    #   2.start参数:开始的参数，默认为0（不写start那就是从0开始）
    #   3.enumerate函数有两个返回值，第一个返回值为从start参数开始的数，第二个参数为iteration参数中的值。
    for index, value in enumerate(li):
        if value == val:
            return index
        else:
            return None

??
??
??

2.二分查找

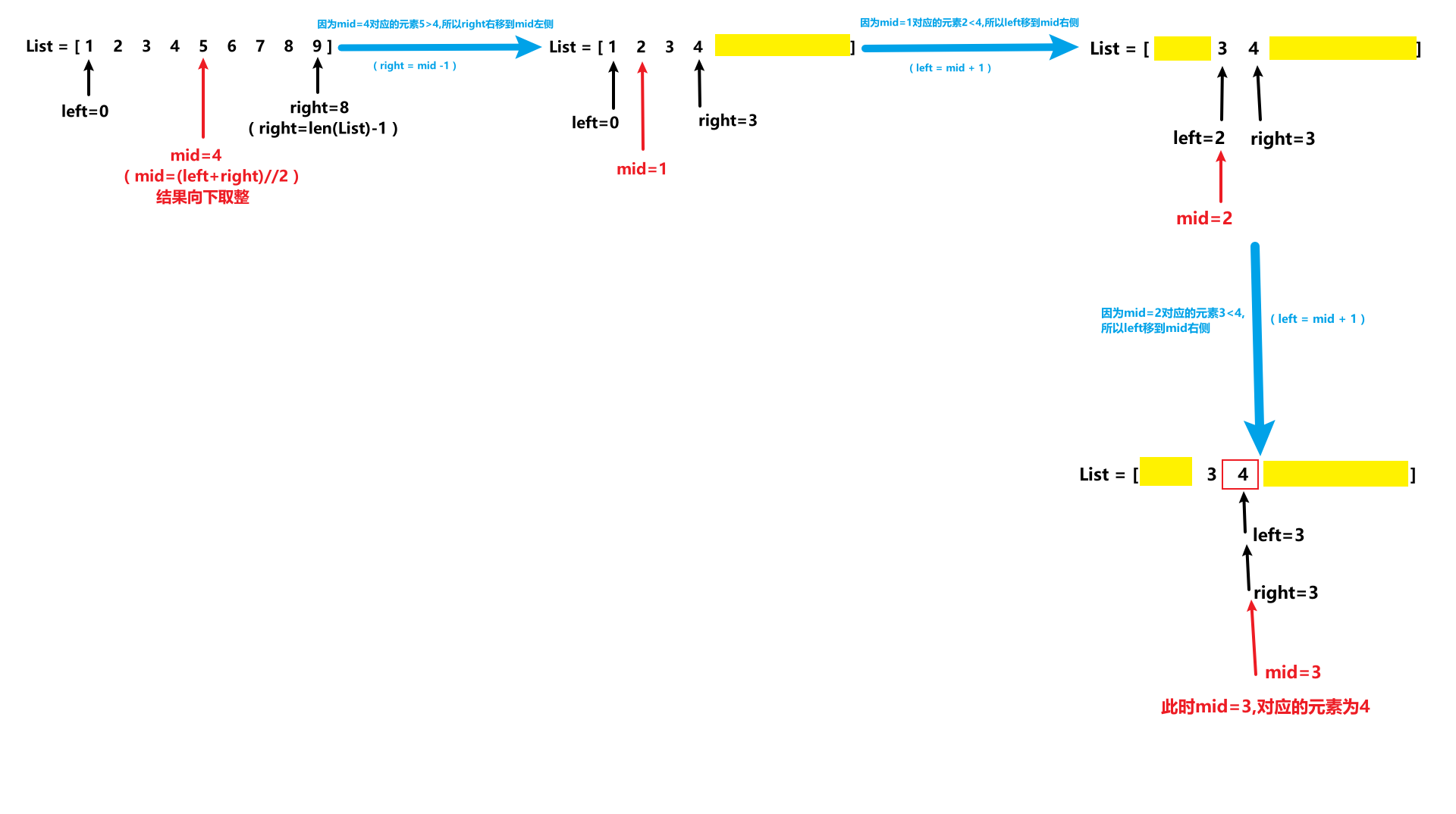
二分查找 (Binary Search) : 也称折半查找, 针对一个有序数据集合, 每次都通过跟区间的中间元素对比, 将待查找的区间缩小为之前的一半, 直到找到要查找的元素, 或者区间被缩小为 0.
二分查找图解 : 从列表中查找元素3.

图片/数据结构与算法9.png

二分查找时间复杂度 : O(logn)
二分查找与顺序查找比较 : 二分查找的效率远高于顺序查找.

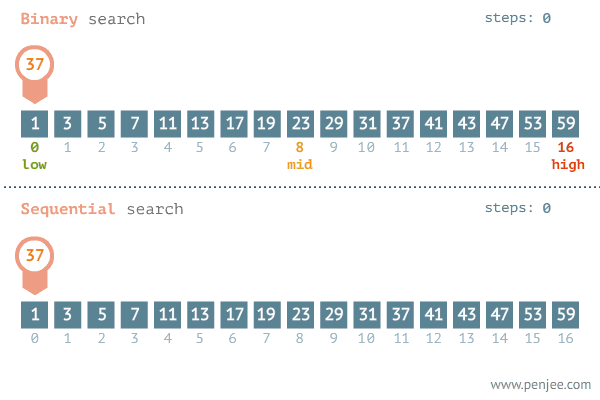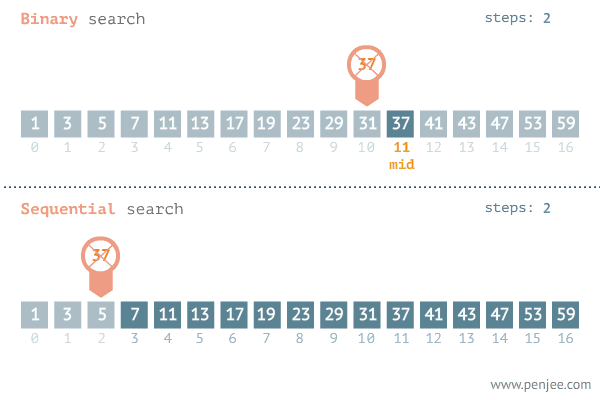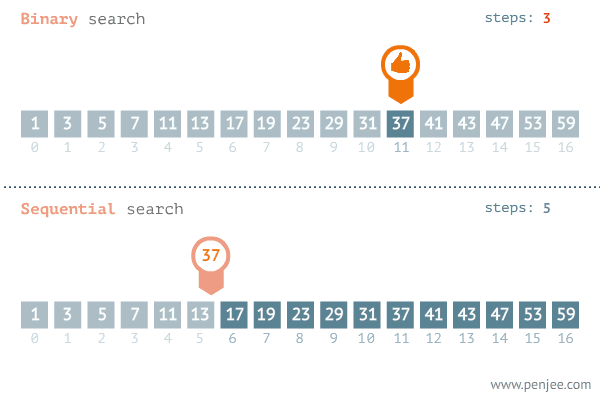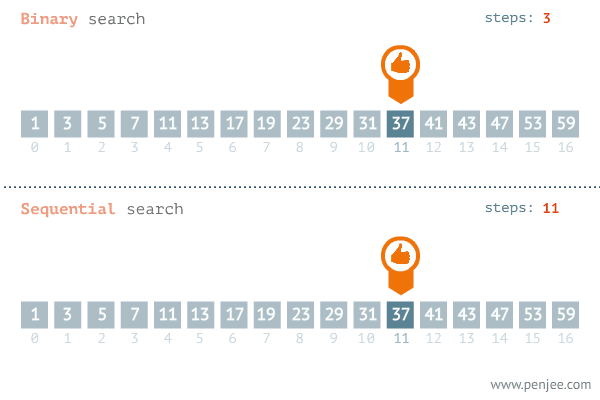
图片/数据结构与算法8.gif

二分查找的局限性 :
- 二分查找针对的是有序数据, 也就是说我们使用二分查找前必须对数据进行排序.
- 数据量太小和太大都不适用于二分查找, 太小可以直接用顺序查找, 太大电脑内存撑不住.

# -*- coding: utf-8 -*-

def binary_search(li, val):
    left = 0
    right = len(li) - 1

    # 候选区有值
    while left <= right:
        mid = (left + right) // 2
        if li[mid] == val:
            return mid
        # 待查找的值在mid左侧
        elif li[mid] > val:
            right = mid - 1
        # 待查找的值在mid右侧
        else:
            left = mid + 1
    else:
        return None

??
??

知识点七 : 排序

排序 : 将一组 “无序” 的记录序列调整为 “有序” 的记录序列
列表排序 : 将无序列表变为有序列表
- 输入 : 列表
- 输出 : 有序列表
升序与降序
- 升序 : 按从小到大的顺序排列 (如1、3、5、6、7、9)
- 降序 : 按从大到小的顺序排列 (如9、8、6、4、3、1)
内置排序函数 : sort( )
常见排序算法 :
- 排序 Low B 三人组排序NB三人组其他排序
  1.冒泡排序 1.快速排序 1.希尔排序
  2.选择排序 2.堆排序 2.计数排序
  3.插入排序 3.归并排序 3.基数排序

??
??

1.冒泡排序

冒泡排序 (Bubble Sort):
- 列表每两个相邻的数, 如果前面比后面大, 则交换这两个数
- 一趟排序完成后, 则无序区减少一个数, 有序区增加一个数
- 代码关键点 : 趟、无序区范围
- 执行 n-1 趟 ( n是列表的长度 )
冒泡排序的时间复杂度 : O(n²)
冒泡排序实例 :

初始数据：[ 30,13,25,16,47,26,19,29,10 ]

第一趟执行过程（先从30依次开始比较）：

0 1 2 3 4 5 6 7 8
13 30 25 16 47 26 19 29 10
13 25 30 16 47 26 19 29 10
13 25 16 30 47 26 19 29 10
13 25 16 30 47 26 19 29 10
13 25 16 30 26 47 19 29 10
13 25 16 30 26 19 47 29 10
13 25 16 30 26 19 29 47 10
13 25 16 30 26 19 29 10 47
第一趟 : [13 25 16 30 26 19 29 10 47]

第二趟：[13 16 25 26 19 29 10 30 47]

…

第八趟: [10 13 16 19 25 26 29 30 47]

注意点1 : 冒泡排序相当于是一个接力，从最左侧的一个记录（30）开始从左到右开始比较，遇到比自己小的数就将其甩在身后（放到30的左边），遇到比自己大的数就把接力棒交给它（40），直到这一趟中的最大记录到达最右侧，然后开始新一轮接力跑（上一趟的最大记录不再参与此趟）

# -*- coding: utf-8 -*-

import random


def bubble_sort(li):
    # 第i趟
    for i in range(len(li) - 1):
        for j in range(len(li) - i - 1):
            exchange = False
            # >是执行升序排序,<是执行降序排序
            if li[j] > li[j + 1]:
                li[j], li[j + 1] = li[j + 1], li[j]
                exchange = True

        # print(f"第{i+1}趟:{li}")

        # if not exchange 的意思是 if not False,因为我们之前将False这个值赋给了exchange这个变量
        if not exchange:
            return


li = [random.randint(0, 100) for i in range(10)]

print(f"执行冒泡排序前:{li}")
bubble_sort(li)
print(f"执行冒泡排序后:{li}")

??
??

2.选择排序

选择排序 (Select Sort) : 一趟排序记录最小的数, 将其放到第一个位置; 再一趟排序记录列表无序区最小的数, 放到第二个位置.
选择排序算法关键点 : 有序区和无序区、无序区最小数的位置
选择排序的时间复杂度 : O(n²)

# -*- coding: utf-8 -*-

# 选择排序简单版
# 缺陷:开辟了新的存储空间,算法的利用率低
import random


def select_sort_simple(li):
    li_new = []
    for i in range(len(li)):
        min_val = min(li)
        li_new.append(min_val)
        li.remove(min_val)
    return li_new


li = [random.randint(0,100) for i in range(10)]
print(f"执行简单选择排序前:{li}")
print(f"执行简单选择排序后:{select_sort_simple(li)}")

# -*- coding: utf-8 -*-

import random

# 选择排序完整版
def select_sort(li):
    # i = 0,1,2,3,4,5,6,7,8
    for i in range(len(li)-1):
        min_loc = i
        # i+1少比一次,因为我们设的最开始的最小值为i,相当于减少了它自己跟自己比的那一趟
        # j = 1,2,3,4,5,6,7,8,9
        for j in range(i+1, len(li)):
            # 现在在li列表中j就是i的后一个下标,只要j对应的那个元素比i现在对应的那个元素小,两者就交换位置
            if li[j] < li[min_loc]:
                min_loc = j
        li[i], li[min_loc] = li[min_loc], li[i]
        # print(li)


li = [random.randint(0,100) for i in range(10)]
print(f"执行选择排序前:{li}")
select_sort(li)
print(f"执行选择排序后:{li}")