1. 两个链表的第一个重合节点
给定两个单链表的头节点 headA 和 headB ,请找出并返回两个单链表相交的起始节点。如果两个链表没有交点,返回 null 。
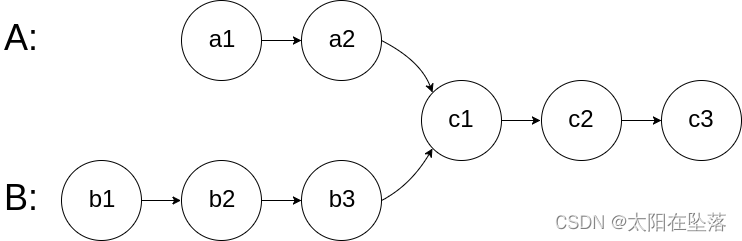
分析:
首先像个用哈希表来实现,但效率低
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
Set<ListNode> set = new HashSet<>();
ListNode node = headA;
while (node != null){
set.add(node);
node = node.next;
}
node = headB;
while (node != null){
if (set.contains(node)) return node;
node = node.next;
}
return null;
}
}
想要实现O(1)的空间复杂度,可以使用双指针来做。定义两个指针A和B分别初始化为headA和headB,当A和B不为null时:A=A.next,B=B.next;A为null令其等于headB,B为null令其等于headA。A=B时跳出循环。
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
if (headA == null || headB == null) return null;
ListNode p1 = headA, p2 = headB;
while (p1 != p2){
p1 = p1==null?headB:p1.next;
p2 = p2==null?headA:p2.next;
}
return p1;
}
}
2. 链表中环的入口节点
给定一个链表,返回链表开始入环的第一个节点。 从链表的头节点开始沿着 next 指针进入环的第一个节点为环的入口节点。如果链表无环,则返回 null。
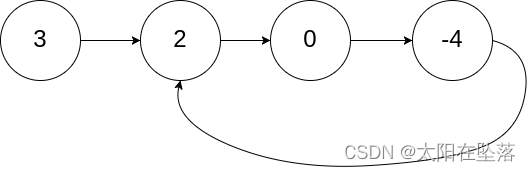
分析:
首先想到的还是哈希表:
public class Solution {
public ListNode detectCycle(ListNode head) {
Set<ListNode> set = new HashSet<>();
ListNode node = head;
while (node != null){
if (!set.contains(node)) {
set.add(node);
node = node.next;
}
else return node;
}
return null;
}
}
想要实现O(1)空间使用快慢指针:
使用两个指针,fast 与 slow。它们起始都位于链表的头部。随后,slow 指针每次向后移动一个位置,而 fast 指针向后移动两个位置。如果链表中存在环,则fast 指针最终将再次与 slow 指针在环中相遇。
当发现 slow 与 fast 相遇时,我们再额外使用一个指针 ptr。起始它指向链表头部;随后,它和 slow 每次向后移动一个位置。最终,它们会在入环点相遇。
public class Solution {
public ListNode detectCycle(ListNode head) {
if (head == null) {
return null;
}
ListNode slow = head, fast = head;
while (fast != null) {
slow = slow.next;
if (fast.next != null) {
fast = fast.next.next;
} else {
return null;
}
if (fast == slow) {
ListNode ptr = head;
while (ptr != slow) {
ptr = ptr.next;
slow = slow.next;
}
return ptr;
}
}
return null;
}
}
3. 删除链表中倒数第n个节点
给定一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
分析:
快慢指针。设置一个辅助头节点,方便删除操作,简化代码,将辅助头结点.next 指向 head。
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode head1 = new ListNode(0);
head1.next = head;
ListNode pre = null, cur = head1;
for (int i = 1; i < n; i++) {
cur = cur.next;
}
ListNode node = head1;
while (cur.next != null){
cur = cur.next;
pre = node;
node = node.next;
}
pre.next = node.next;
return head1.next;
}
}
4. 回文子字符串的个数
给定一个字符串 s ,请计算这个字符串中有多少个回文子字符串。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
分析:
遍历字符串,对每个字符,都看作回文的中心,向两端延申进行判断直到非回文。回文的中心可能是一个字符,也可能是两个字符。注意双指针可能越界。
class Solution {
public int countSubstrings(String s) {
if (null == s || s.length()==0) {
return 0;
}
int res = 0;
for (int i = 0; i < s.length(); i++) {
res += isPalindrome(s, i, i);
res += isPalindrome(s, i, i+1);
}
return res;
}
public int isPalindrome(String s, int start, int end) {
int count = 0;
while (start>=0 && end<s.length() && s.charAt(start) == s.charAt(end)) {
count++;
start--;
end++;
}
return count;
}
}
5. 最大层内元素和
给你一个二叉树的根节点 root。设根节点位于二叉树的第 1 层,而根节点的子节点位于第 2 层,依此类推。
请返回层内元素之和最大的那几层(可能只有一层)的层号,并返回其中最小的那个。
分析:
层次遍历,遍历每一层时计算节点值之和。
class Solution {
public int maxLevelSum(TreeNode root) {
if (root==null) return 0;
Deque<TreeNode> queue = new LinkedList<>();
int level = 0, maxSum = Integer.MIN_VALUE, res = 0;
queue.addLast(root);
while (!queue.isEmpty()){
int size = queue.size();
level++;
int sum = 0;
while (size>0){
TreeNode node = queue.pollFirst();
sum += node.val;
if (node.right!=null) queue.addLast(node.right);
if (node.left!=null) queue.addLast(node.left);
size--;
}
if (sum > maxSum){
res=level;
maxSum = sum;
}
}
return res;
}
}