?(?˙o˙?)? 大家好, 欢迎大家光临我的博客:面向阿尼亚学习
算法学习笔记系列持续更新中~

前言
?干翻动态规划问题
动态规划问题描述及思路
动态规划(Dynamic Programming),无非就是利用历史记录,来避免我们的重复计算。而这些历史记录,我们得需要一些变量来保存,一般是用一维数组或者二维数组来保存。
算法的核心思想是:将大问题划分为小问题进行解决,从而一步步获取最优解的处理算法
第一步骤:定义数组元素的含义,上面说了,我们会用一个数组,来保存历史数组,假设用一维数组 dp[] 吧。这个时候有一个非常非常重要的点,就是规定你这个数组元素的含义,例如你的 dp[i] 是代表什么意思?
第二步骤:找出数组元素之间的关系式,我觉得动态规划,还是有一点类似于我们高中学习时的归纳法的,当我们要计算 dp[n] 时,是可以利用 dp[n-1],dp[n-2]……dp[1],来推出 dp[n] 的,也就是可以利用历史数据来推出新的元素值,所以我们要找出数组元素之间的关系式,例如 dp[n] = dp[n-1] + dp[n-2],这个就是他们的关系式了。而这一步,也是最难的一步
第三步骤:找出初始值。学过数学归纳法的都知道,虽然我们知道了数组元素之间的关系式,例如 dp[n] = dp[n-1] + dp[n-2],我们可以通过 dp[n-1] 和 dp[n-2] 来计算 dp[n],但是,我们得知道初始值啊,例如一直推下去的话,会由 dp[3] = dp[2] + dp[1]。而 dp[2] 和 dp[1] 是不能再分解的了,所以我们必须要能够直接获得 dp[2] 和 dp[1] 的值,而这,就是所谓的初始值。
有了初始值,并且有了数组元素之间的关系式,那么我们就可以得到 dp[n] 的值了,而 dp[n] 的含义是由你来定义的,你想求什么,就定义它是什么**
以上可以看出:
动态规划算法与分治算法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。
与分治法不同的是,适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的。 ( 即下一个子阶段的求解是建立在上一个子阶段的解的基础上,进行进一步的求解 )
练几个题吧~!
1. 爬梯子
题目描述:
一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
思路:
最基础的动态规划问题
1.首先我们来定义 dp[i] 的含义
dp[i]表示跳上一个 i 级的台阶总共有 dp[i] 种跳法。
2.状态转移方程
由于情况可以选择跳一级,也可以选择跳两级,所以青蛙到达第 n 级的台阶有两种方式
一种是从第 n-1 级跳上来
一种是从第 n-2 级跳上来
由于我们是要算所有可能的跳法的,所以有 dp[n] = dp[n-1] + dp[n-2]。
3.找出初始条件
当 n = 1 时,dp[1] = dp[0] + dp[-1],而我们是数组是不允许下标为负数的,所以对于 dp[1],我们必须要直接给出它的数值,相当于初始值,显然,dp[1] = 1。一样,dp[0] = 0.(因为 0 个台阶,那肯定是 0 种跳法了)。
AC代码及注释:
#include <iostream>
using namespace std;
int main()
{
int n;
cin>>n;
int dp[n];
//初始化
dp[0]=0;
dp[1]=1;
for(int i=2;i<=n;i++)
{
//状态转移方程
dp[i]=dp[i-1]+dp[i-2];
}
cout<<dp[n]<<endl;
return 0;
}
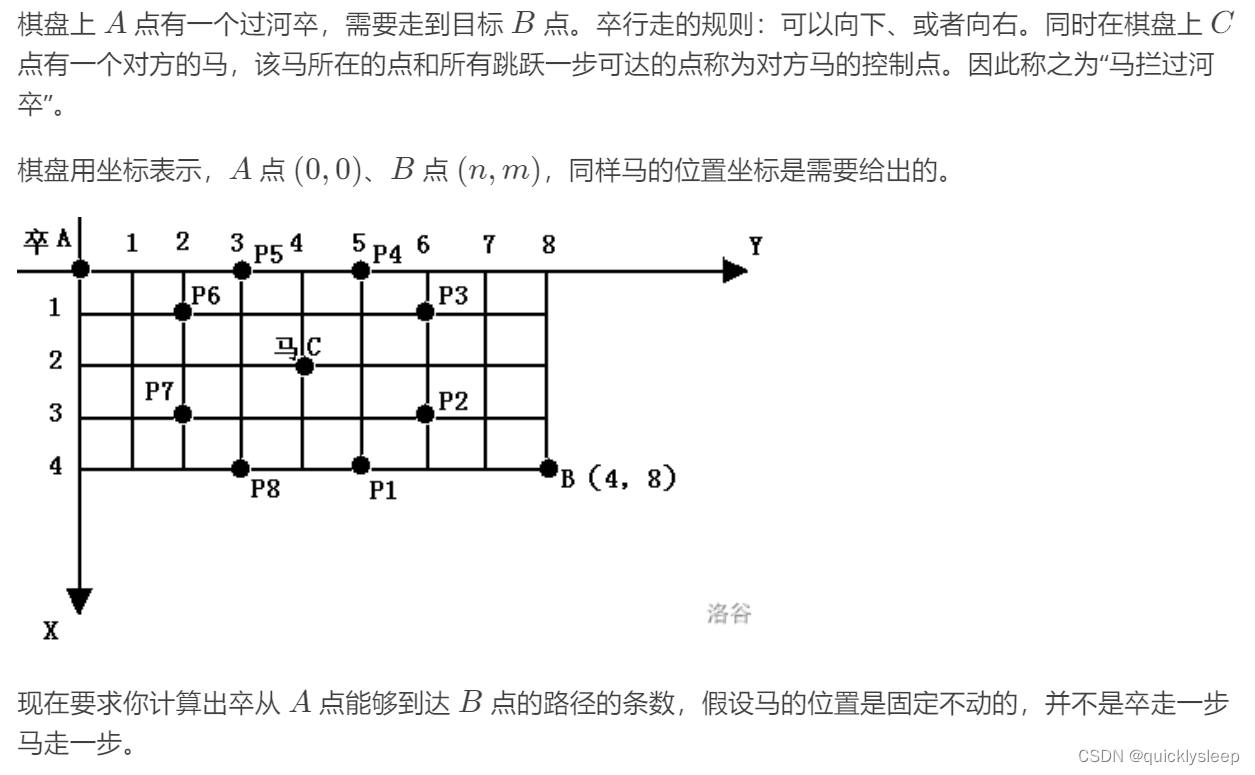
2. 过河卒
🔗 过河卒
题目描述
思路:
卒只能向下或向右走,易得状态转移方程f(i,j)=f(i-1,j)+f(i,j-1)
为方便解题,给棋盘加1的偏移量,标记马可以走的位置为-1判断即可
AC代码及注释:
#include<iostream>
#include<algorithm>
using namespace std;
long long dp[30][30];
int mx[8]={-2,-2,-1,-1,1,1,2,2},my[8]={1,-1,2,-2,2,-2,1,-1};//马的偏移量
int main(){
int n,m,x,y;
cin>>n>>m>>x>>y;
n+=1;m+=1;x+=1;y+=1;//整体加一行一列,便于边界检查
for(int i=0;i<8;i++){
if(x+mx[i]>=1&&x+mx[i]<=n&&y+my[i]>=1&&y+my[i]<=m)
dp[x+mx[i]][y+my[i]]=-1;//-1表示不能走
}
dp[1][0]=1;//根据dp(1,1)=dp(0,1)+dp(1,0)
//我们只需要让dp(0,1)=1或者dp(0,1)=1即可
dp[x][y]=-1;//马所在的点也不能走
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(dp[i][j]==-1)
dp[i][j]=0;
else{
dp[i][j]=dp[i-1][j]+dp[i][j-1];
}
}
}
cout<<dp[n][m];
return 0;
}
3.砝码称重
🔗砝码称重
题目描述:

思路:
f[i]表示 “重量 i 成立”
三重循环遍历找所有成立的
AC代码及注释:
#include <bits/stdc++.h>
using namespace std;
const int N=1001;
int a[7],w[7]={0,1,2,3,5,10,20},f[N];
//a数组存放的是每种砝码的数量,w数组是每种砝码的重量,f[i]表示 “重量 i 成立”
int main()
{
for (int i=1;i<=6;i++)//输入
{
cin>>a[i];
}
f[0]=1;
for (int i=1;i<=6;i++)//枚举六种砝码
{
for (int j=1;j<=a[i];j++)//枚举每个砝码
{
for (int k=1000;k>=0;k--)//寻找 已成立的重量
{
if (f[k])//若此重量成立
{
f[k+w[i]]=1;//那么这个重量加上这个未使用的砝码的总重量也成立
}
}
}
}
int ans=0;
for (int i=1;i<=1000;i++)
{
if (f[i]) ans++;
}
cout<<"Total="<<ans<<endl;
return 0;
}
4.2022
题目描述:

思路:
相比上一题,这个要求拆分成十个数字,还要等于2022,本题使用二维DP
dp[j][k]表示j个数相加等于k的方法个数
结果可能会很大,所以要开long long
AC代码及注释:
#include <iostream>
using namespace std;
typedef long long LL;
LL dp[11][2025];
int main()
{
dp[0][0]=1;
for(int i=1;i<=2022;i++)
{
for(int j=10;j>=1;j--)
for(int k=1;k<=2022;k++)
if(k>=i)//避免重复
dp[j][k]+=dp[j-1][k-i];
}
cout<<dp[10][2022]<<endl;
}
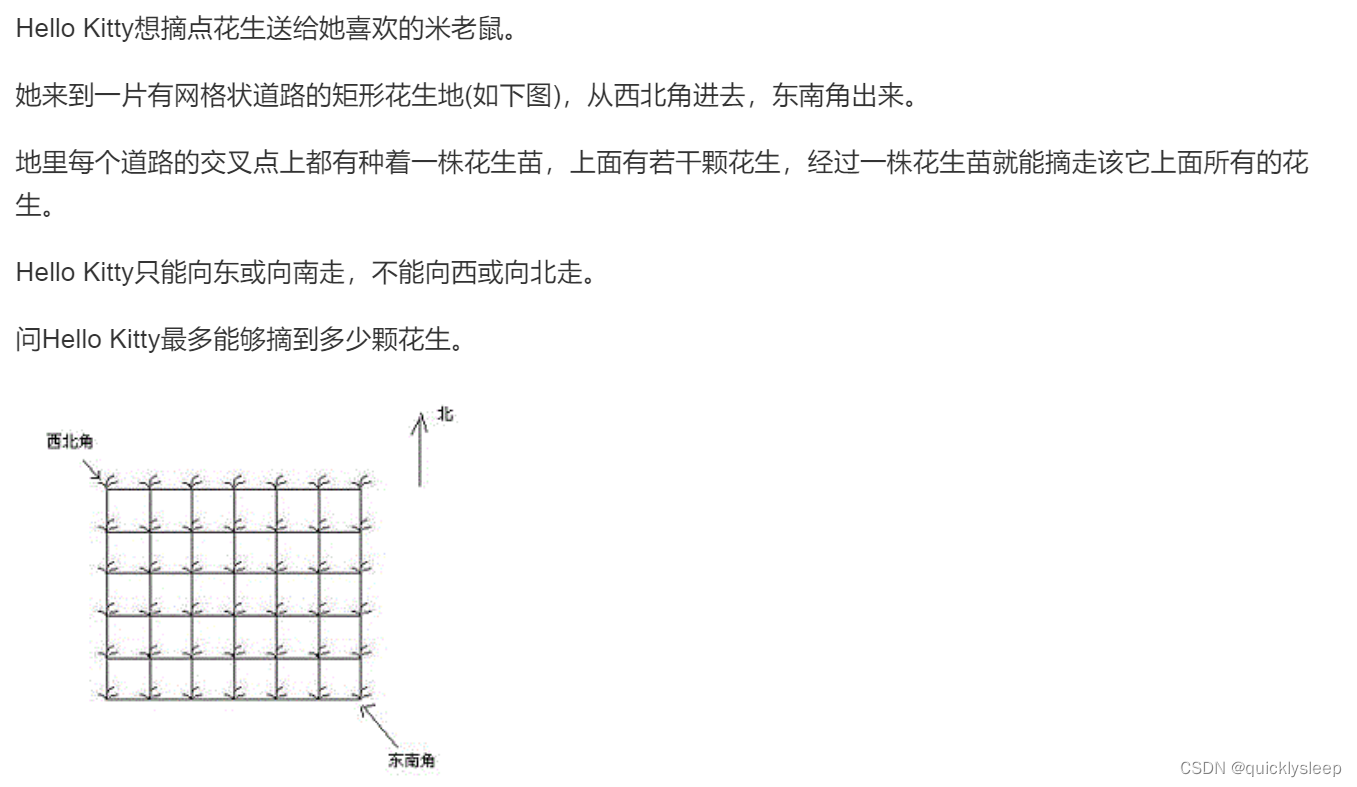
5. 摘花生
🔗摘花生
题目描述:
思路:
本题求最大的数字和
dp[i][j]表示到(i,j)位置的最大和
可以从左方以及上方下来,所以
状态转移方程为 dp[i][j] = max(dp[i][j-1] + a[i][j], dp[i-1][j] + a[i][j]);
AC代码及注释:
#include <iostream>
#include <cstring>
int a[1007][1007];
int dp[1007][1007];
using namespace std;
int main()
{
int t;
cin>>t;
while(t--)
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
cin>>a[i][j];
}
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
dp[i][j]=max(dp[i-1][j]+a[i][j],dp[i][j-1]+a[i][j]);
}
}
cout<<dp[n][m]<<endl;
}
return 0;
}
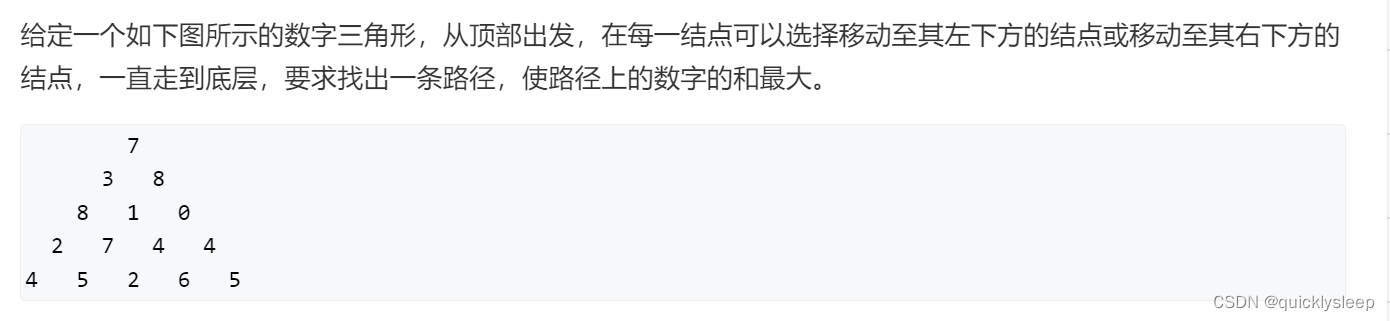
6. 数字三角形
题目描述:
思路:
本题求最大的数字和
dp[i][j]表示到(i,j)位置的最大和
可以从左上方以及上方下来,所以
状态转移方程为 dp[i][j] = max(dp[i-1][j-1] + a[i][j], dp[i-1][j] + a[i][j]);
AC代码及注释:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 510, INF = 1e9;
int n;
int a[N][N], dp[N][N];
int main() {
cin >> n;
//输入
for (int i = 1; i <= n; i++)
for (int j = 1; j <= i; j++)
cin>>a[i][j];
//初始化
for (int i = 0; i <= n; i++)
for (int j = 0; j <= i + 1; j++) // 每行需要多初始化一个,考虑到两边
dp[i][j] = -INF;
dp[1][1] = a[1][1];
for (int i = 2; i <= n; i++) // 若从1开始,结果为负无穷,由前状态转移而来
for (int j = 1; j <= i; j++) // 从2开始才有前状态
dp[i][j] = max(dp[i-1][j-1] + a[i][j], dp[i-1][j] + a[i][j]);//状态转移方程
int res = -INF;
for (int i = 1; i <= n; i++) res = max(res, dp[n][i]);//在最下一行取最大
cout << res << endl;
return 0;
}
也可以从下往上进行dp,不用考虑边界
#include<bits/stdc++.h>
using namespace std;
const int N=510;
int dp[N][N];
int n;
int main(){
cin>>n;
for(int i=1;i<=n;i++){
for(int j=1;j<=i;j++){
cin>>dp[i][j];
}
}
for(int i=n;i>=1;i--){
for(int j=i;j>=1;j--){
dp[i][j]=max(dp[i+1][j],dp[i+1][j+1])+dp[i][j];
}
}
cout<<dp[1][1]<<endl;
}
最后
