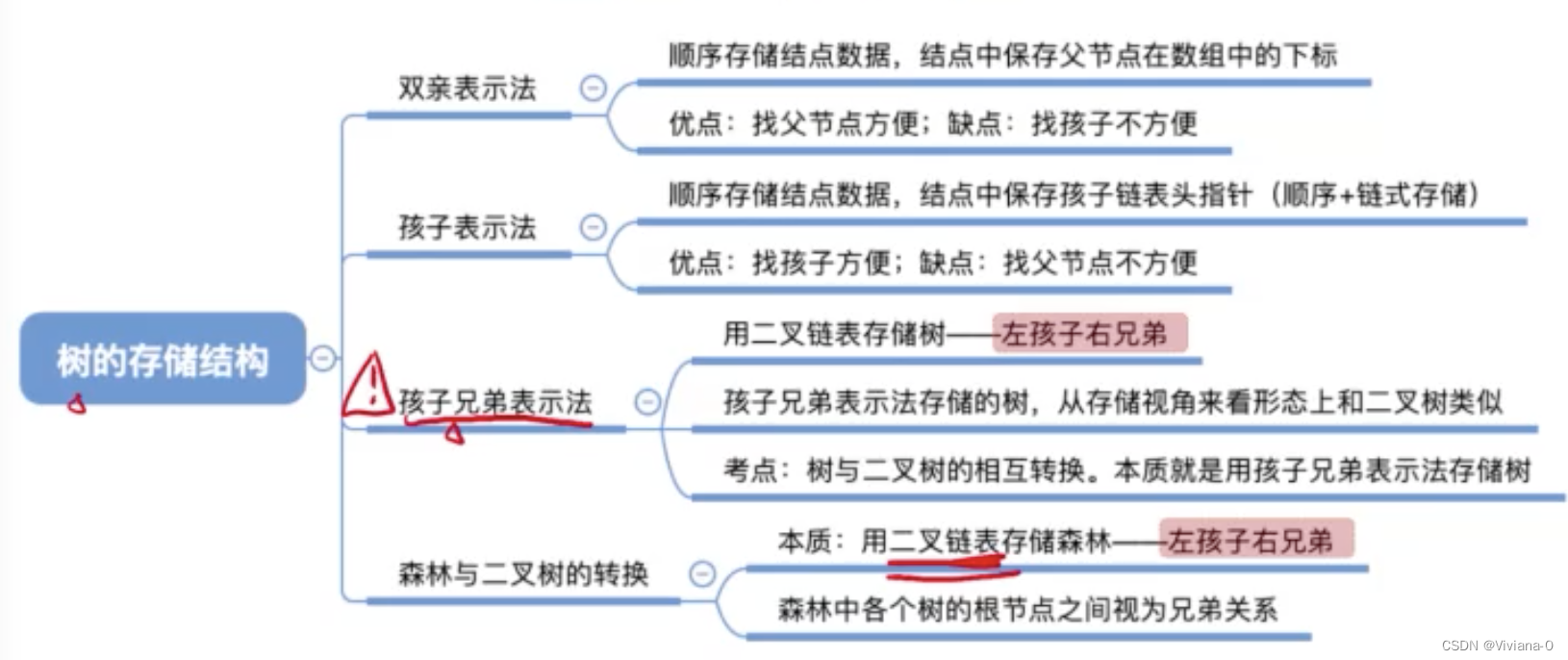
一、树的存储结构
树的存储方式又多种,既可以采用顺序存储结构,又可采用链式存储结构,但是无论用何种存储方式,都要求能唯一地反映树中各节点之间的逻辑关系
树的3种常见的存储结构
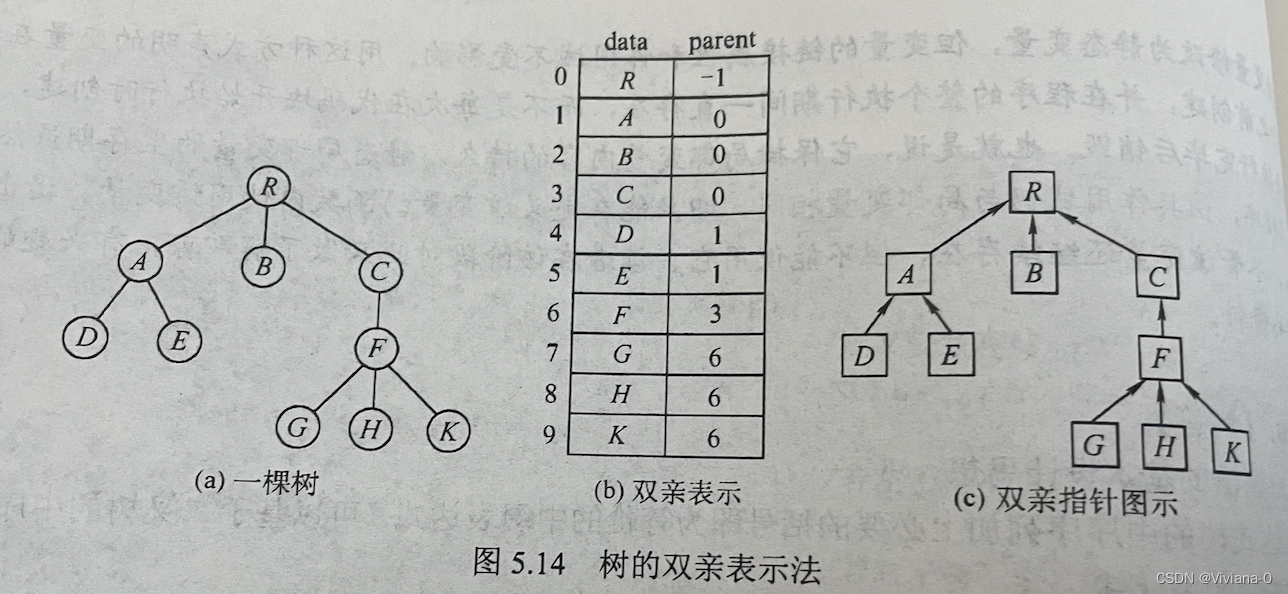
1.1双亲表示法
优点:查指定结点的双亲结点很方便
缺点:查指定结点的孩子只能从头遍历整个结构
注意:区别树和二叉树之间的顺序存储结构:
- 在树的顺序存储中,数组下标代表结点的编号,下标中所存的内容指示了
结点直接的关系; - 二叉树的顺序存储中,数组既代表了结点的编号,又指示了
二叉树各结点之间的关系;(意思就是怎么找左孩子怎么找右孩子)
二叉树也是属于树,因此二叉树可以用树的存储结构来存储,但树却不都能用二叉树的存储结构来存储
- 存储方法:
采用一组连续空间来存储每个结点,同时在每个结点中增设一个伪指针,指示其双亲结点在数组中的位置
根结点的固定存储为下标为0,其伪指针域为-1
当需要删除结点的时候:
方法1:可以将指针域设置为-1(但是空数据会导致遍历更慢)
方法2:将要删除的设置为空,将最尾部的信息填充上去,第二种方法就可以保证前面的存储都是有效的
(但是如果不是叶子结点则就很麻烦了)
1.2孩子表示法(是顺序存储和链式存储的结合)
优点:寻找孩子操作非常直接简单
缺点:寻找双亲就很复杂
用一片顺序的空间,来顺序存储各个结点的数据,每个结点中除了存放数据域还需要存储指向他第一个孩子的指针,即n个结点就有n个孩子链表(叶子结点的孩子链表为空表)
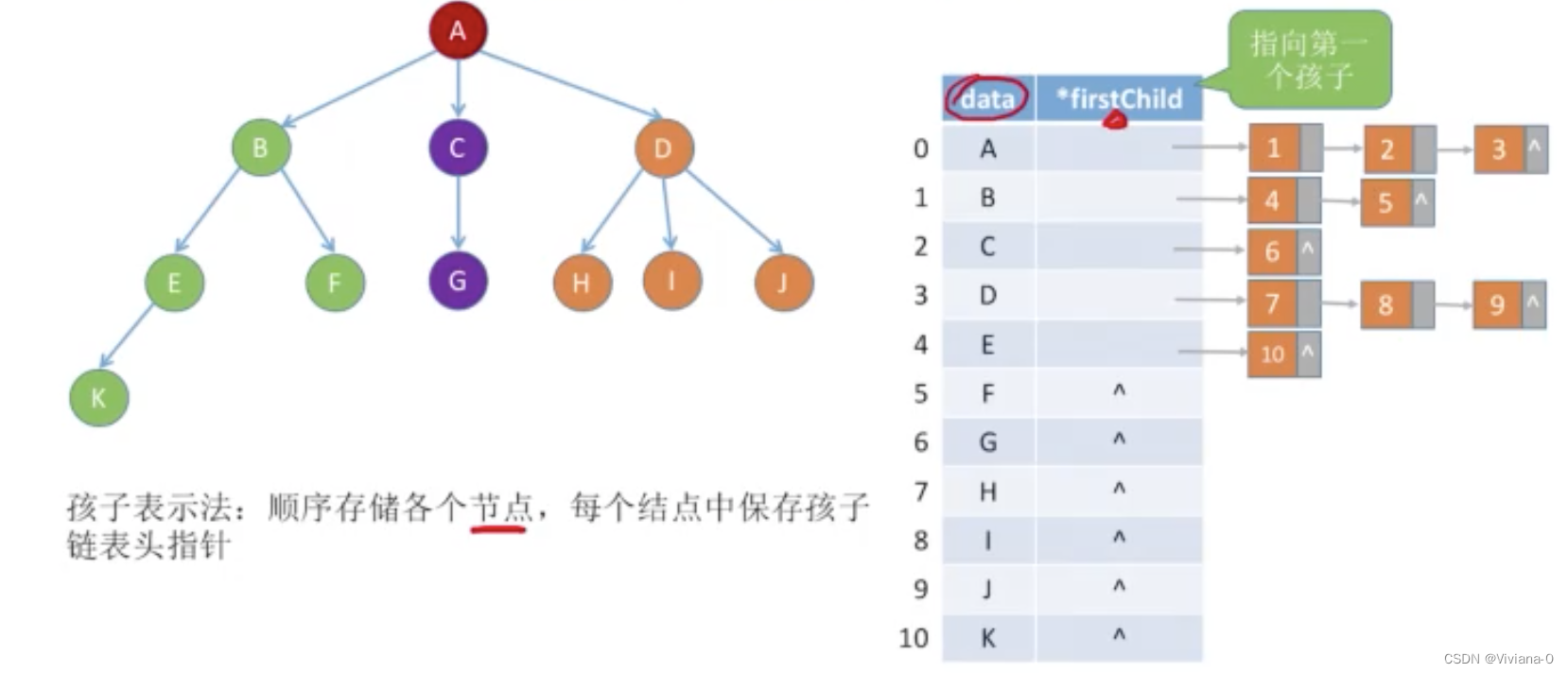
1.3孩子兄弟表示法(链式存储)类似树与二叉树的转换
优点:可以方便地实现树转换为二叉树的操作,易于查找结点的孩子等,但缺点是从当前结点查找其双亲结点比较麻烦。可以用我们熟悉的二叉树来处理树
孩子兄弟表示法又称为二叉树表示法,即以二叉链表作为树的存储结构
孩子兄弟表示法使得各个结点包括三部分内容:结点值、指向结点第一个孩子结点的指针,及指向结点下一个兄弟结点的指针(沿此域可以找到结点的所有兄弟结点)
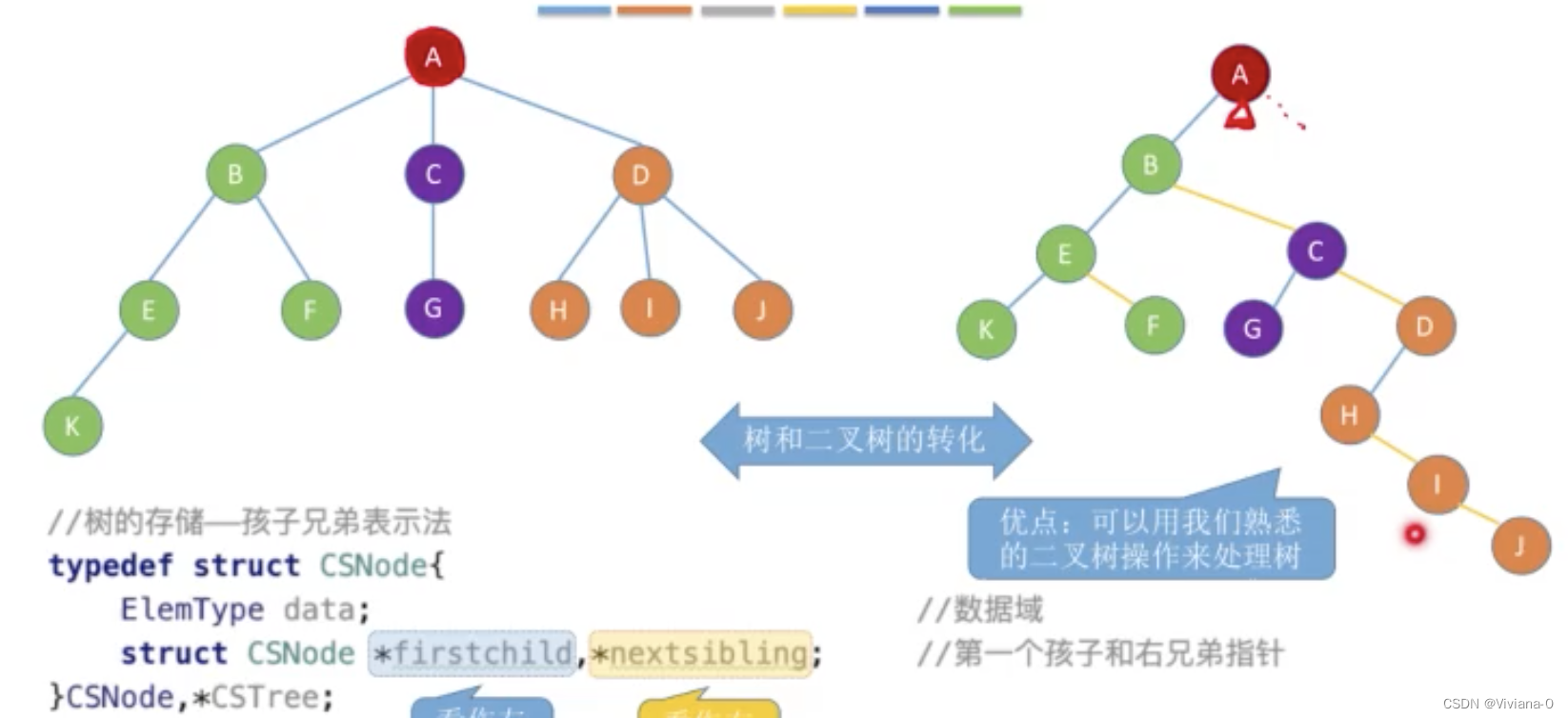
将firstchild看作做左指针、nextsibling看作右指针
由于B结点是A结点的第一个孩子,所以链接在A的左指针
由于C结点是B结点的右兄弟,所以链接在B右边指针
由于D结点C结点的右兄弟,所以链接在C右边指针
举例子:
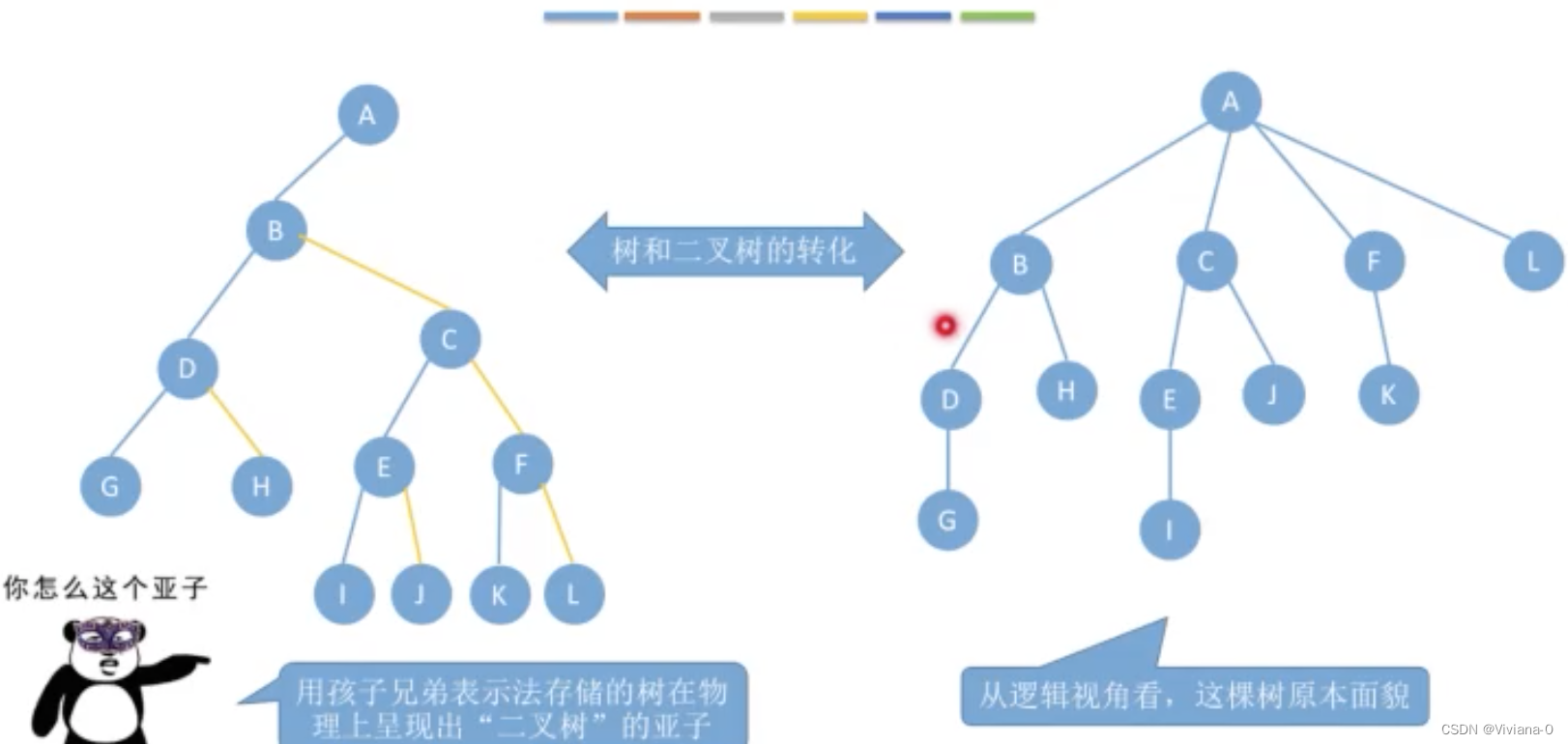
二、森林与二叉树的转换
2.1森林和二叉树的转换
本质:用二叉链表存储森林-----左孩子右孩子,森林中各个树的根结点之间视为兄弟关系
举例1:
- 首先将森林依次转换为二叉树
- 从逻辑上看各个树的根结点是平级关系,因此可以看做兄弟关系
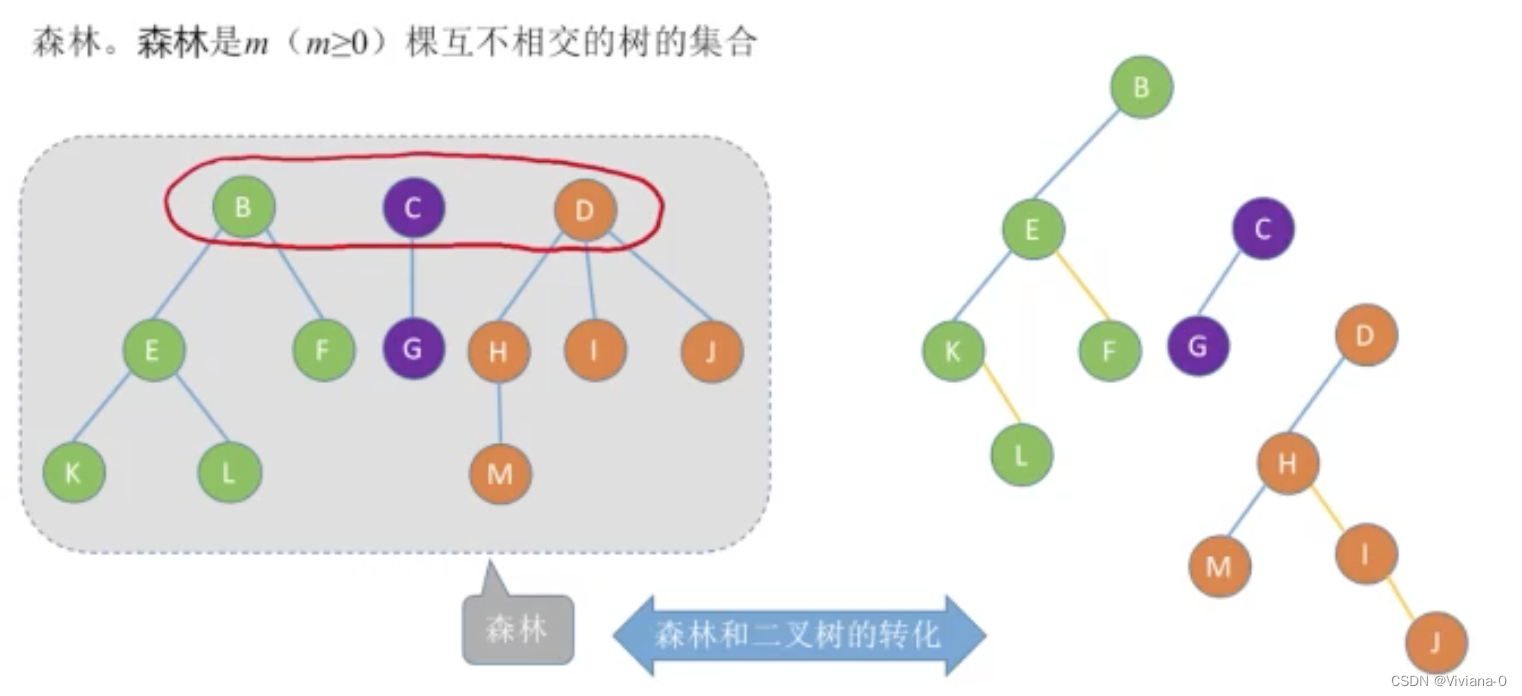
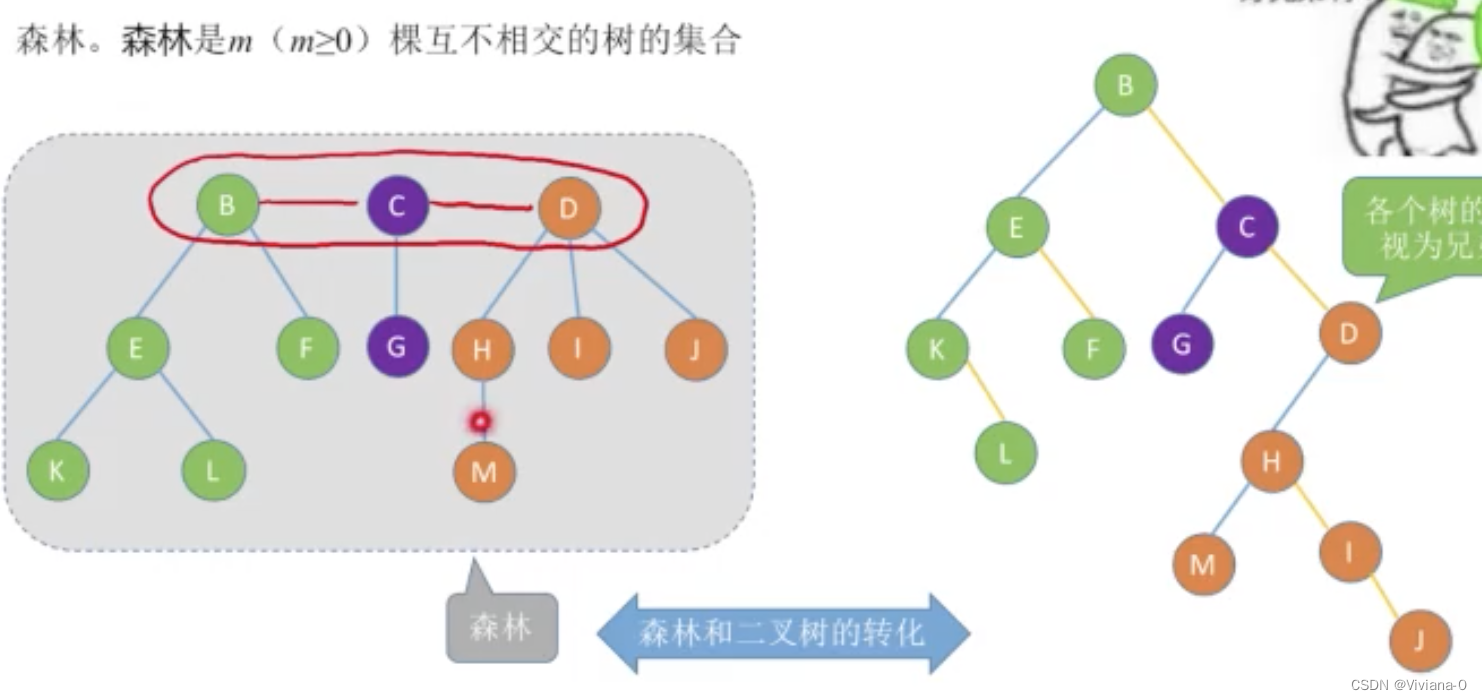
举例2:
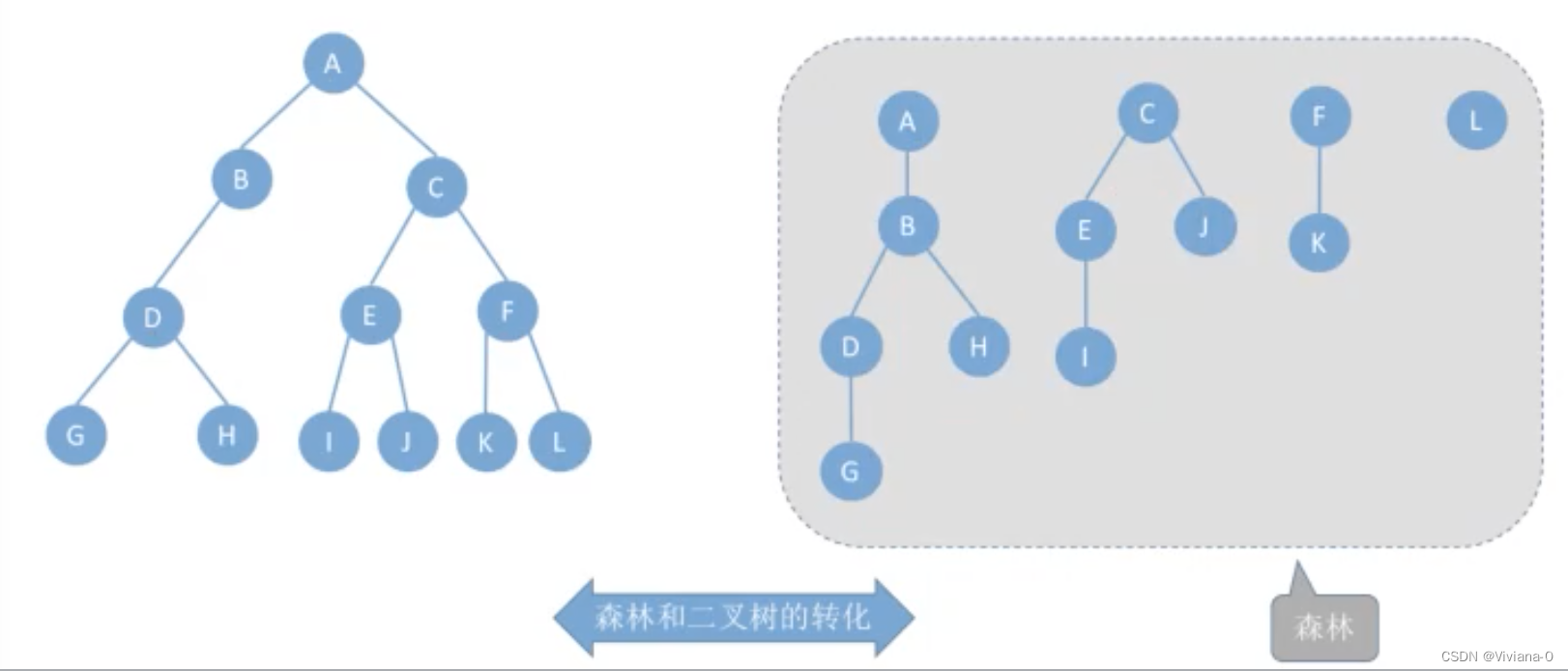
三、树和森林的遍历
3.1树的遍历
是指用某种方式访问树中的每个结点,且仅访问一次,主要有两种方式:
先根遍历
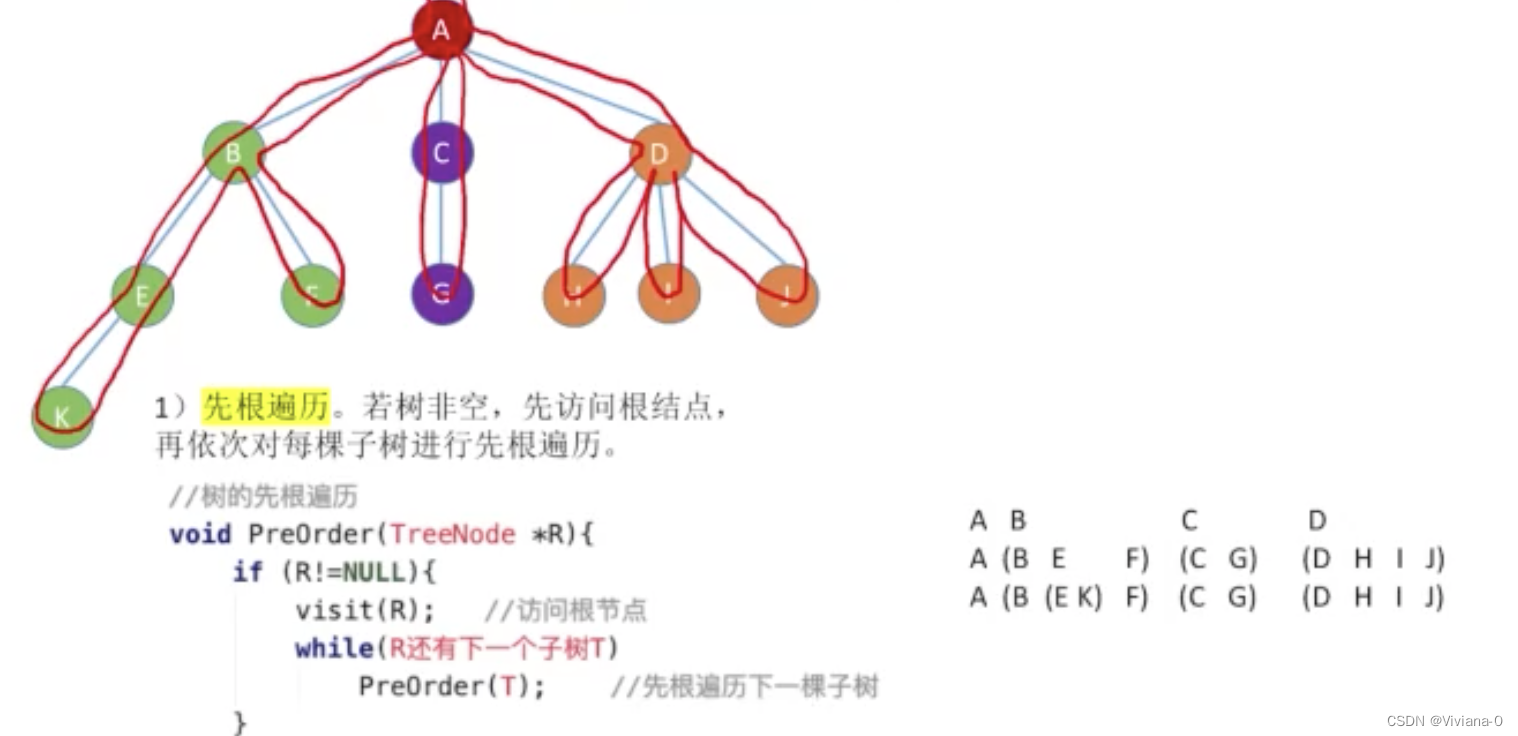
后根遍历
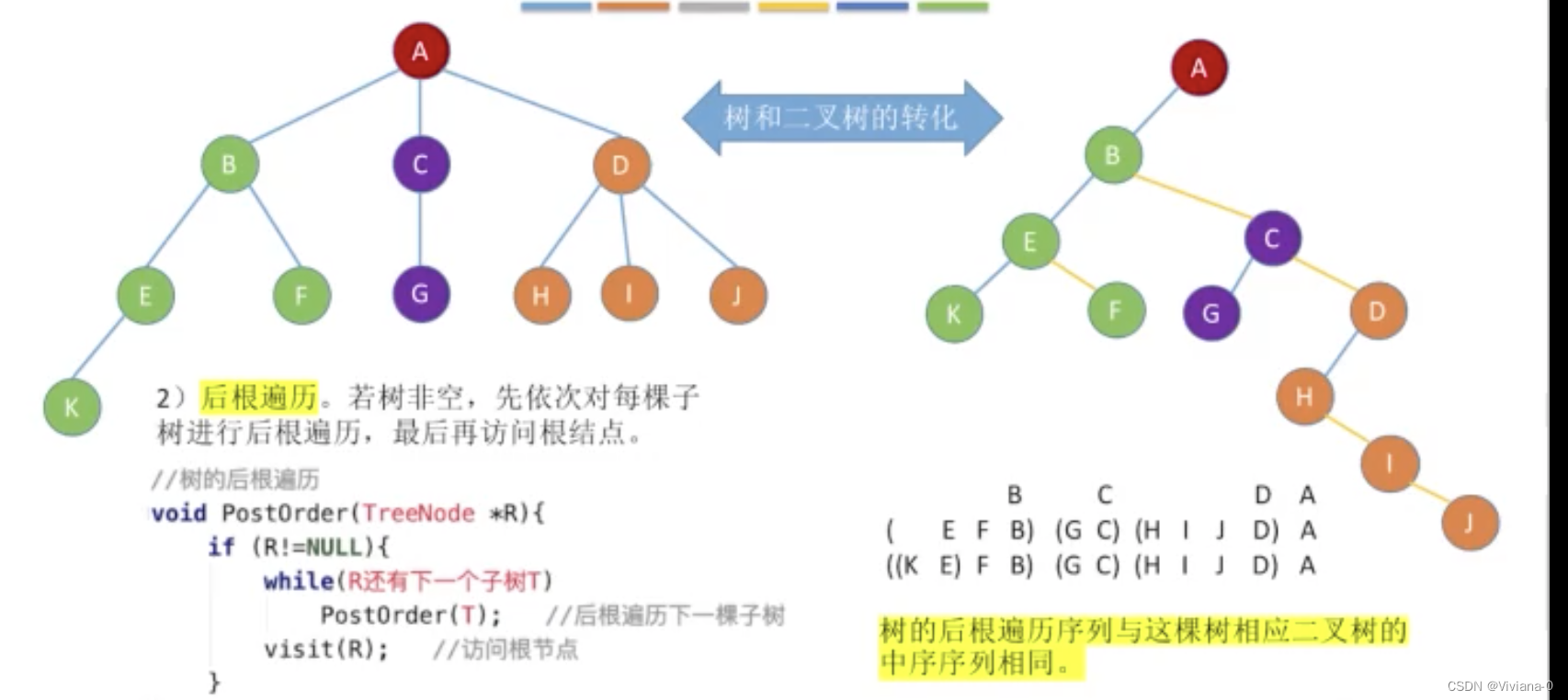
层次遍历:与二叉树的层次遍历思想基本相同
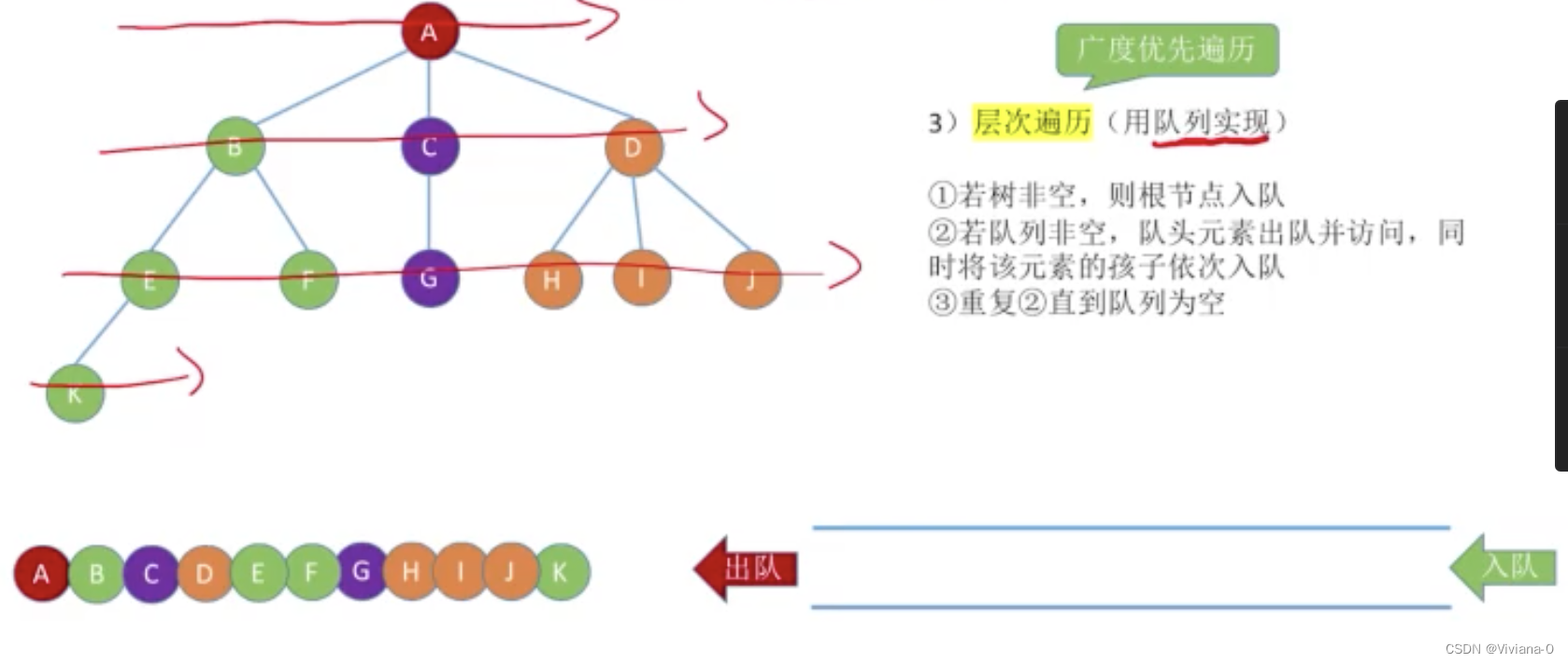
3.2森林的遍历
先序遍历森林
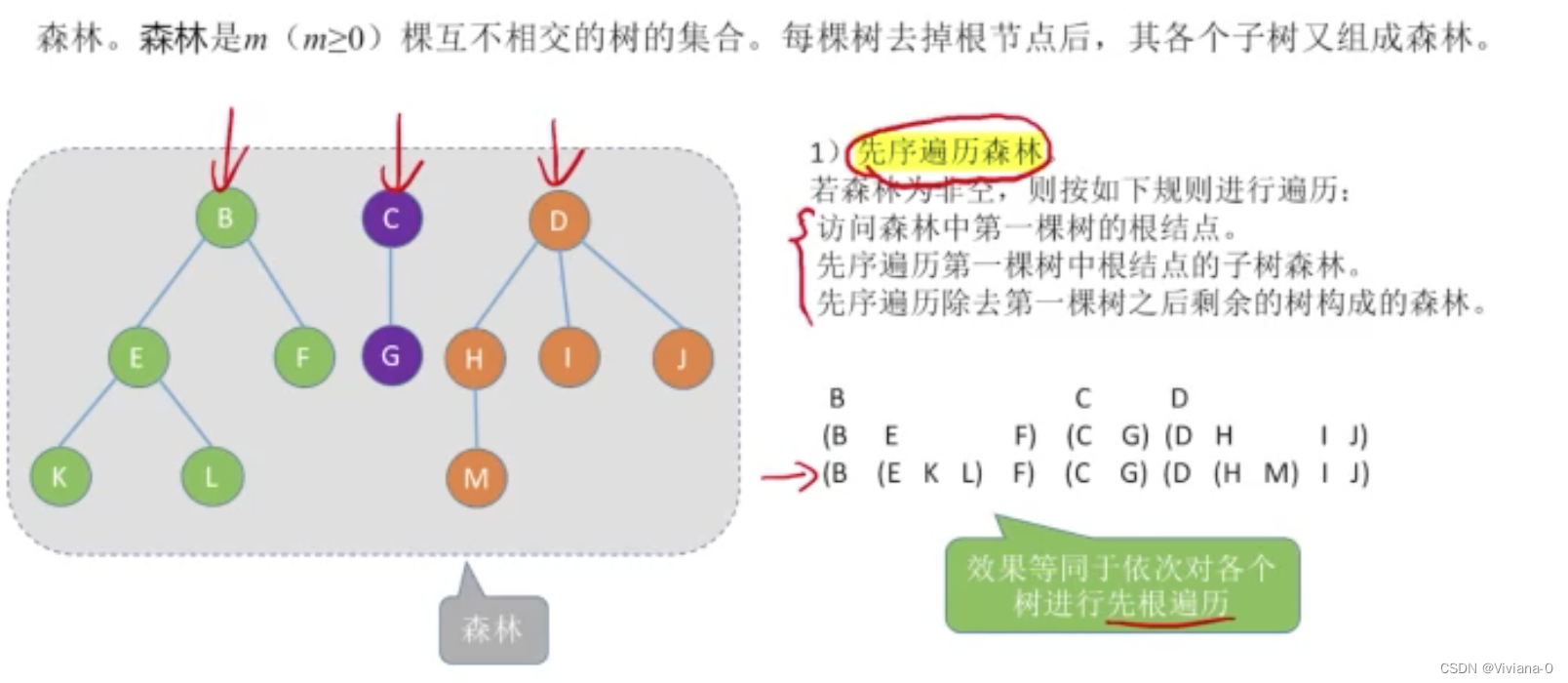

中序遍历森林
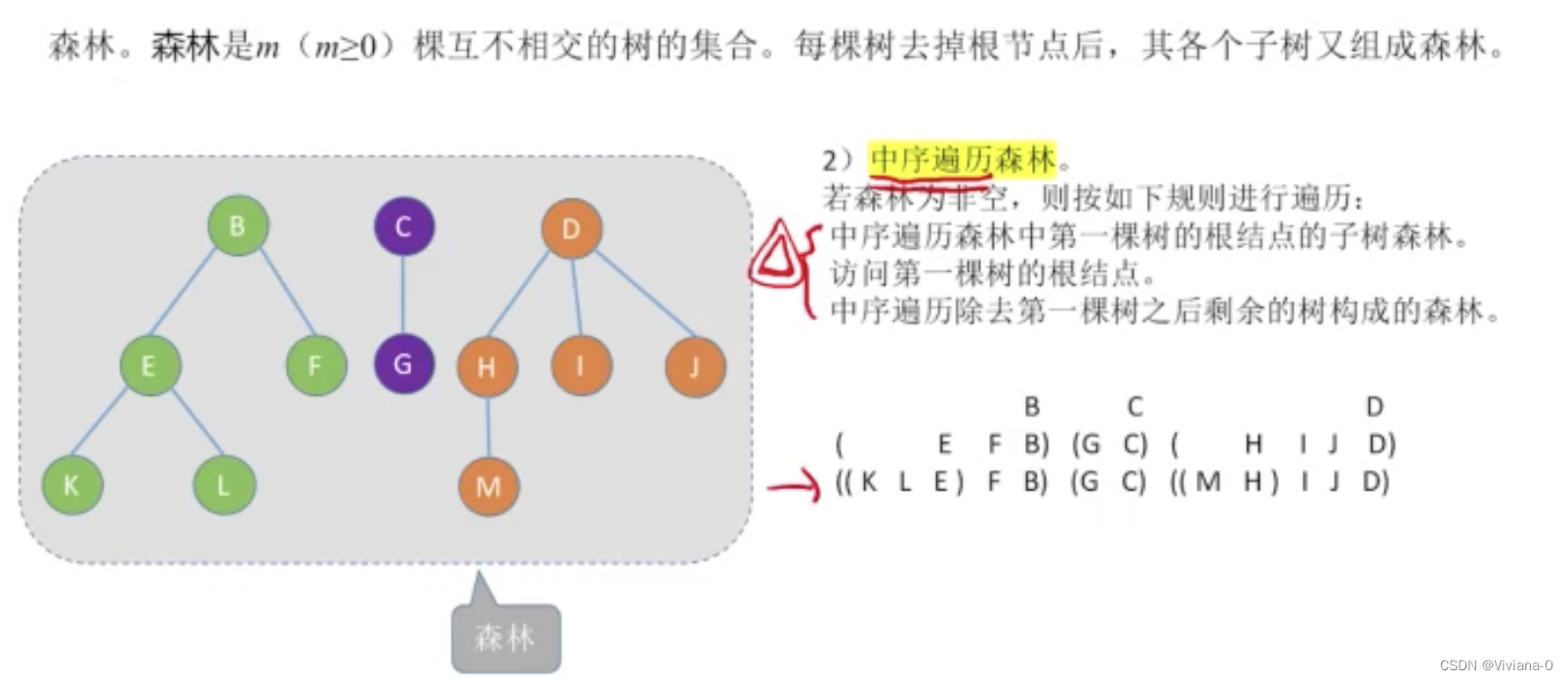
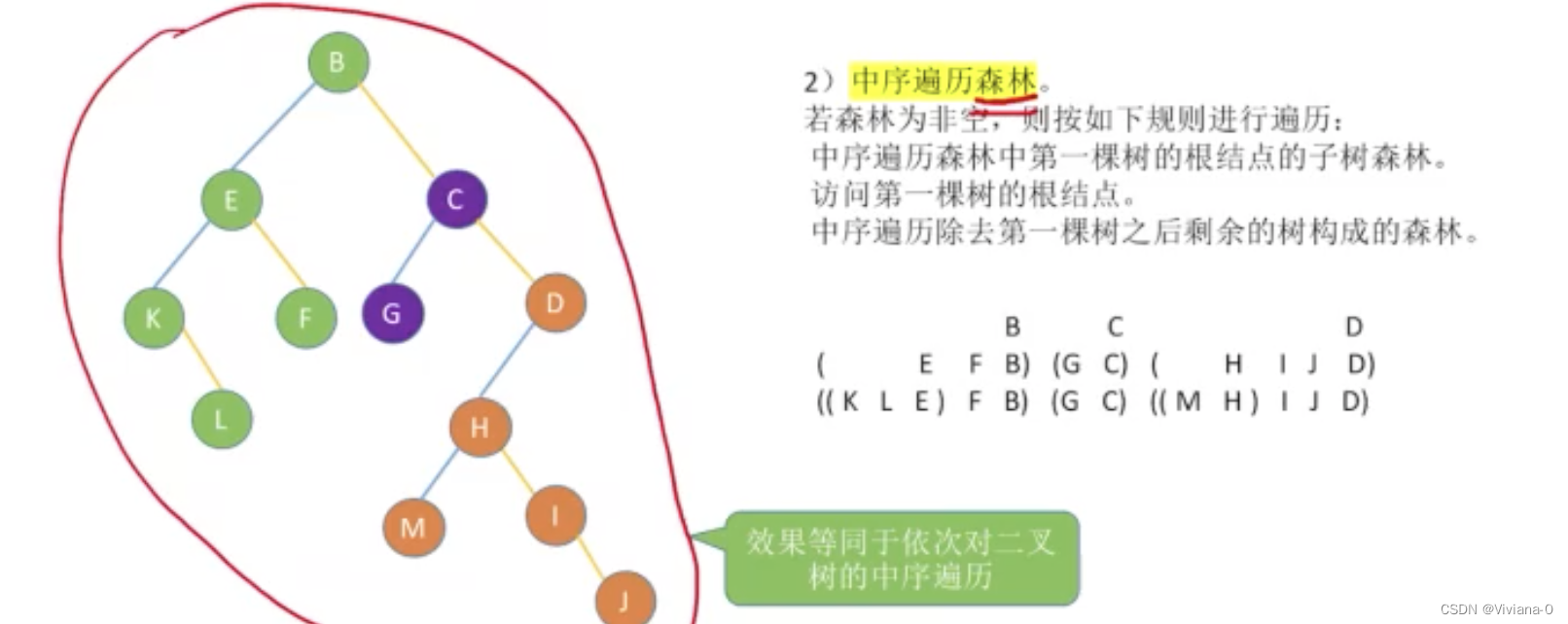
树和森林的遍历与二叉树的遍历
中根遍历也可以称为后根遍历
