[数据结构与算法]【算法】七大排序详解(下篇)

5.希尔排序

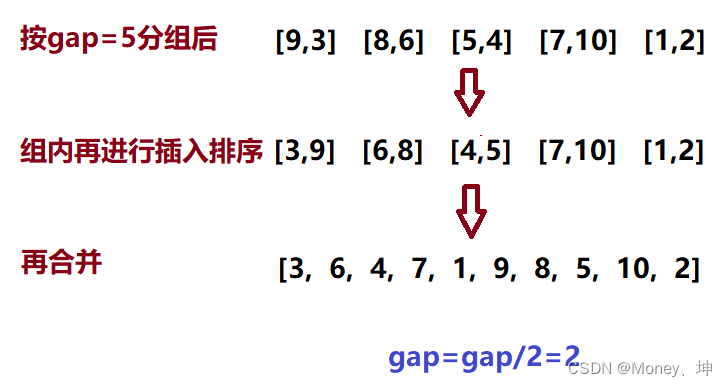
排序思路：又称缩小增量排序，给定一个数值gap，将原数组按照gap分为若干个组，组内再进行插入排序，直到gap=1，整个数组已经被调整的接近有序，最后再全集和上进行一次插入排序即可；
时间复杂度：O（n^1.3~1.5）
稳定性：不稳定

排序思路：

1.将待排序数组按gap分组

2.将分组后的数组组内进行插入排序，最后再合并

3.继续以上操作，直至gap=1

4.最后gap=1，整个数组已经接近有序，最后在数组内进行一次插入排序，整个数组的排序完成

代码实现：

 /**
     * 希尔排序
     * 时间复杂度：O(N^1.3-1.5)   不稳定
     * @param arr
     */
    public static void shellSort(int[] arr){
        int gap =arr.length>>1;
        while (gap>1){
            //预处理阶段，将原数组按gap分组，组内进行插入排序
            insertSortByGap(arr,gap);
            gap /=2;
        }
        //此时gap=1,直接插入排序即可
        insertSort(arr);
    }
    /**
     * 直接插入排序
     * 每次从无序区间取一个值插入到已排序的区间，直到整个序列有序
     * 时间复杂度 O（N^2） 性能稳定
     * @param arr
     */
    public static void insertSort(int[] arr){
        //已排序区间：[0,i)   未排序区间：[i,n]
        for (int i=1;i<arr.length;i++){
            //简易写法
            for (int j=i;j>0 &&arr[j]<arr[j-1];j--){
                swap(arr,j,j-1);
            }
        }
    }
    /**
     * 按gap分组进行插入排序
     * @param arr
     * @param gap
     */
    private static void insertSortByGap(int[] arr, int gap) {
        for (int i=gap;i<arr.length;i++){
            for (int j=i; j-gap >=0 && arr[j]<arr[j-gap]; j-=gap){
                swap(arr,j,j-gap);
            }
        }
    }
    /**
     * 交换数组arr中索引 i 和 j 的索引位置
     */
    private static void swap(int[] arr, int i, int j) {
        int temp =arr[i];
        arr[i] =arr[j];
        arr[j]=temp;
    }

6. 归并排序

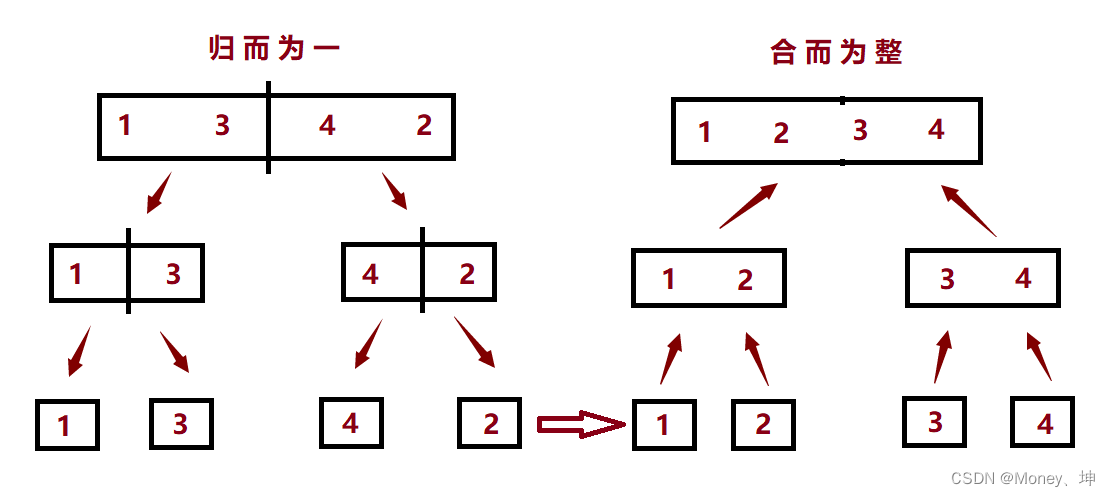
排序思路：归并排序，分为两个过程，一是归而为一，就是将原数组不断拆分，直至数组元素个数为1；二是合而为整，就是将拆分的数组不断合并，同时合并的过程中将数组有序化。
时间复杂度：O（nlogN）
稳定性：稳定
排序过程：

代码实现：

    /**
     * 归并排序
     * @param arr
     */
    public static void mergeSort(int[] arr){
        //递归函数
        mergeSortInternal(arr,0,arr.length-1);
    }

    /**
     * 在区间 [l , r]上进行归排序
     * @param arr
     * @param l
     * @param r
     */private static void mergeSortInternal(int[] arr, int l, int r) {
        if (r-l <=15){
            //小区间上直接使用插入排序
            insertSort(arr,l,r);
        }
        int mid =l+((r-l)>>1);            //相当于（l+r）/2
        //递归再左区间[l，mid]上归并排序
        mergeSortInternal(arr,l,mid);
        //在右区间上[mid+1,r]上归并排序
        mergeSortInternal(arr,mid+1,r);
        //走完上述递归，左右区间已经有序，最后进行合并
        if (arr[mid] >arr[mid+1]){
            merge(arr,l,mid,r);
        }
    }

    /**
     * 在区间[l , r]上进行插入排序
     * @param arr
     * @param l
     * @param r
     */
    private static void insertSort(int[] arr, int l, int r) {
        for (int i=l+1;i<=r;i++){
            for (int j=i; j>l&& arr[j]<arr[j-1];j--){
                swap(arr,j,j-1);
            }
        }
    }
    /**
     * 交换数组arr中索引 i 和 j 的索引位置
     */
    private static void swap(int[] arr, int i, int j) {
        int temp =arr[i];
        arr[i] =arr[j];
        arr[j]=temp;
    }

    /**
     * 合并两个子数组arr[l...mid]和arr[mid+1，r]
     * 为一个大的有序数组
     * @param arr
     * @param l
     * @param mid
     * @param r
     */private static void merge(int[] arr, int l, int mid, int r) {
        //1.先创建一个临时数组
        int[] temp=new int[r-l+1];
        //2.再将原数组的值拷贝到临时数组
        for (int i=0;i<temp.length;i++){
            //临时数组索引从0开始，原数组从l开始，两数组索引差就是l+i；
            temp[i] =arr[i+l];
        }
        // i 表示左侧小区间的开始索引
        int i=l;
        // j 表示右侧区间的开始索引
        int j=mid+1;
        //k 表示当前正在遍历的索引小标
        for (int k=l;k<=r;k++){
            //向后遍历的过程中，i++，当i >mid时，说明左侧区间已经遍历完
            if ( i >mid){
                //此时，左侧区间已经有序，只需拷贝右侧数组
                arr[k]=temp[j-l];
                j++;
            }else if (j > r){
                //向后遍历的过程中，j++，当j >r时，说明右侧区间已经遍历完
                //此时，右侧区间已经被处理完，只需拷贝左侧区间
                arr[k] =temp[i-l];
                i++;
            }else if (temp[i-l] <= temp[j-l]){
                //此时，左侧区间的值较小，相等元素放在左侧，保证稳定性
                arr[k]=temp[i-l];
                i++;
            }else {
                //右侧区间的元素值较小
                arr[k] =temp[j-l];
                j++;
            }
        }

7.快速排序

时间复杂度：O（nlogN）
稳定性：不稳定

排序思路：

• 1.首先选定待排序数组的第一个元素为基准值val

• 2.当 i 向后遍历过程中，分情况讨论

<2.1>如果当前遍历到的元素arr[i] > v 时，i++，红色区域增加即可；

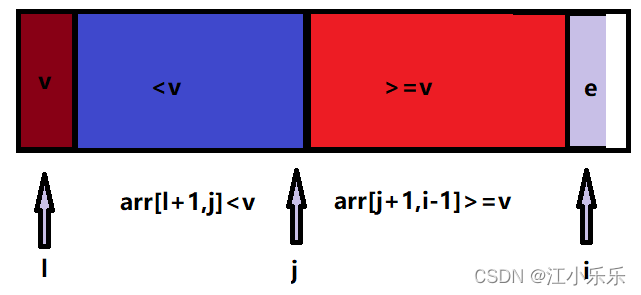
i++后，就把大于等于v的元素加入到红色区域，i继续向后遍历；
<2.2>如果在遍历的过程中，arr[i] <v 时：

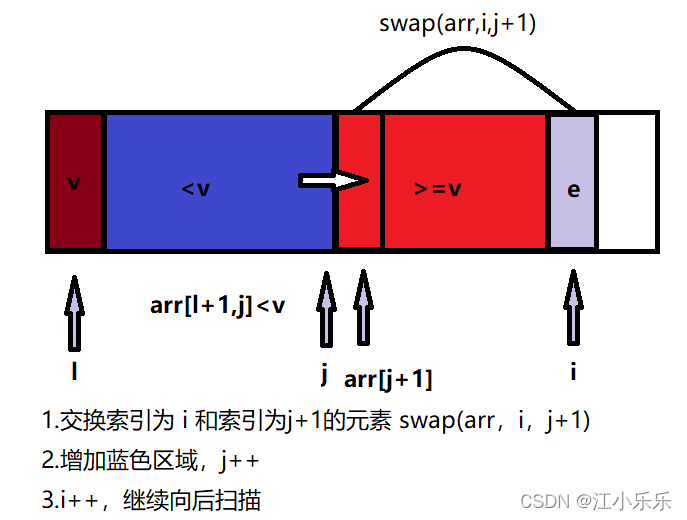
 for (int i = l+1; i <=r ; i++) {
            if (arr[i] <val){
                swap(arr,i,j+1);
                j++;
            }
        }

• 3.整个集合扫描完毕，整个区间就被我们分隔为以下情况：
  
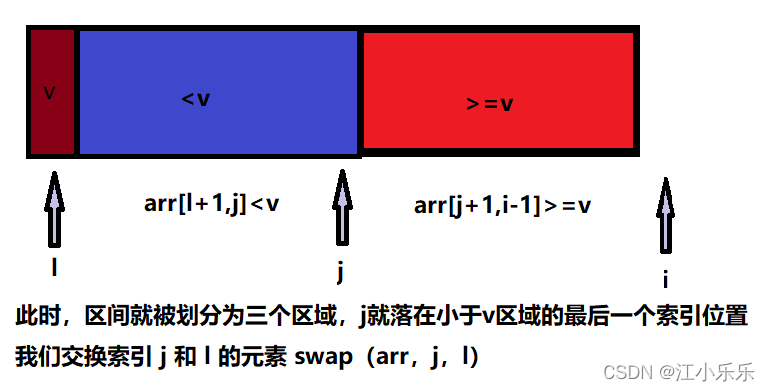
  4.经过以上步骤，arr[j]左侧元素均小于v，arr[j]之后的元素均 大于等于v，分区完成。继续在小于v的区间和大于v的区间继续递归上述过程，直至整个集合有序。

代码实现：

/**
 * 快速排序
 * 时间复杂度：Nlogn
 * 不稳定的排序算法
 */
public class QuickSort {
    /**
     * 快速排序
     * @param arr
     */
    public static void quickSort(int[] arr){
        quickSortInternal(arr,0,arr.length-1);
    }
    /**
     * 在区间【l，r】上进行快速排序
     * @param arr
     * @param l
     * @param r
     */
    private static void quickSortInternal(int[] arr, int l, int r) {
        //先获取分区点：经过分区函数后，某个元素落在了最终的位置
        //分区点左侧元素均小于该元素，分区点右侧元素均大于等于该元素
        if (r-l<=15){
            //优化点，在元素小于15时，直接插入排序优化算法
            insertSort(arr,l,r);        
            return;
        }
        //分区函数,最终返回在[l，r]区间上分区点元素索引
        int p=partition(arr,l,r);
        //在分区元素左侧区间递归
        quickSortInternal(arr,l,p-1);
        //在分区元素右侧区间递归
        quickSortInternal(arr,p+1,r);
    }

    /**
     * 分区函数
     * @param arr
     * @param l
     * @param r
     * @return 分区点索引
     */
    private static int partition(int[] arr, int l, int r) {
        //基准值
        int val=arr[l];
        //arr[l+1...j] < val
        //arr[j+1...i) >= val
        // i 表示当前正在扫描的元素索引
        int j=l;
        for (int i = l+1; i <=r ; i++) {
            if (arr[i] <val){
                swap(arr,i,j+1);
                j++;
            }
        }
        //经过上述循环，就把小于val的元素换到了分区点的左侧
        //此时，将基准值和最后一个小于v的元素交换，基准值就落在了最终的位置
        swap(arr,j,l);
        return j;
    }

    /**
     * 交换数组中 i 和 j 的索引
     * @param arr
     * @param j
     * @param i
     */
    private static void swap(int[] arr, int i, int j ) {
        int temp=arr[i];
        arr[i] =arr[j];
        arr[j] = temp;
    }
    /**
     * 在区间[l , r]上进行插入排序
     * @param arr
     * @param l
     * @param r
     */
    private static void insertSort(int[] arr, int l, int r) {
        for (int i=l+1;i<=r;i++){
            for (int j=i; j>l&& arr[j]<arr[j-1];j--){
                swap(arr,j,j-1);
            }
        }
   	 }
    }

8.算法性能测试

以上算法中，有的时间复杂度是O(N^2),有的则是O（NlogN），这两种时间复杂度的算法，在实际应用中的性能到底是怎样的呢?下面，我们设计算法性能测试用例，来实际感受一下不同算法性能上的优略。

• 定义一个算法测试辅助类，包含生成随机数组、判断数组是否有序、深拷贝数组等方法

import java.lang.reflect.InvocationTargetException;
import java.lang.reflect.Method;
import java.util.Arrays;
import java.util.concurrent.ThreadLocalRandom;

public class SortHelper {
    //获取生成随机数的对象
    private static final ThreadLocalRandom random =ThreadLocalRandom.current();

    /**
     * 在[left,right]的区间上生成一个大小为N的随机数组
     * @return
     */
    public static int[] generateRandomArray(int n,int left,int right ){
        int[] arr =new int[n];
        for (int i = 0; i < arr.length; i++) {
            arr[i]=random.nextInt(left,right);
        }
        return arr;
    }

    /**
     * 生成一个近乎有序的数组
     * @param n
     * @param times     交换的次数，次数越小，数组有序
     * @return
     */
    public static int[] generateSortedArray(int n,int times){
       int[] arr =new int[n];
        for (int i = 0; i < arr.length; i++) {
            arr[i]=i;
        }
        //交换部分元素，使有序数组变得近乎有序
        for (int j = 0; j < times; j++) {
            //生成[0,n]上的随机数
            int a=random.nextInt(n);
            int b=random.nextInt(n);
            int temp =arr[a];
            arr[a]=arr[b];
            arr[b]=temp;
        }
        return arr;
    }

    /**
     * 测试性能的方法，反射的知识
     * 根据传入的方法名称就能对arr数组进行排序
     * @param sortName
     * @param arr
     */
    public static void testSort(String sortName,int[] arr){
        Class<SevenSort> cls =SevenSort.class;      //获取反射对象
        try {
            Method method =cls.getDeclaredMethod(sortName,int[].class);
            long start =System.nanoTime();          //获取系统的时间，纳秒为单位
            method.invoke(null,arr);            //调用方法
            long end =System.nanoTime();
            if (isSorted(arr)){
                //排序正确
                System.out.println(sortName+"排序结束，共耗时："+(end-start)/1000000.0+"ms");
            }
        } catch (NoSuchMethodException e) {
            e.printStackTrace();
        } catch (IllegalAccessException e) {
            e.printStackTrace();
        } catch (InvocationTargetException e) {
            e.printStackTrace();
        }

    }
    /**
     * 生成一个深拷贝的arr数组
     * @param arr
     * @return
     */
    public static int[] arrCopy(int[] arr){
        return Arrays.copyOf(arr,arr.length);
    }
    /**
     * 判断数组是否有序
     * @param arr
     * @return
     */
    public static boolean isSorted(int[] arr){
        for (int i = 0; i < arr.length-1 ; i++) {
            if (arr[i]>arr[i+1]){
                System.out.println("Sort error");
                return false;
            }
        }
        return true;
    }
}

• 选择不同的算法，性能测试

/**
 * 在50000个[0,整形最大值]区间上排序算法的性能测试
 */
public class SortTest {
    public static void main(String[] args) {
        int n=50000;
        int[] arr =SortHelper.generateRandomArray(n,0,Integer.MAX_VALUE);
        int[] arrCopy1 =SortHelper.arrCopy(arr);
        int[] arrCopy2 =SortHelper.arrCopy(arr);
        int[] arrCopy3 =SortHelper.arrCopy(arr);
        int[] arrCopy4 =SortHelper.arrCopy(arr);
        int[] arrCopy5 =SortHelper.arrCopy(arr);
        int[] arrCopy6 =SortHelper.arrCopy(arr);
        SortHelper.testSort("heapSort",arrCopy2);
        SortHelper.testSort("bubbleSort",arrCopy3);
        SortHelper.testSort("selectionSort",arrCopy1);
        SortHelper.testSort("selectionSortOP",arrCopy4);
        SortHelper.testSort("insertionSort",arrCopy5);
        SortHelper.testSort("insertionSortBS",arrCopy6);
    }
}

• 测试结果
  

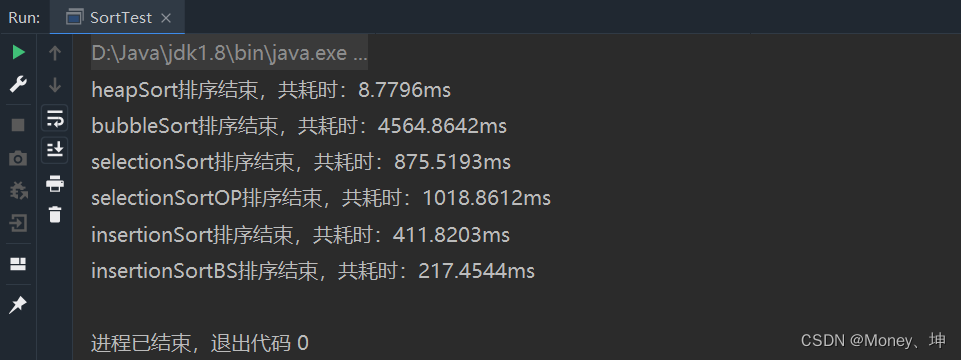
简单总结一下，在长度为50000的数组，数值在【0~整形最大值】的数组上进行排序测试，O（N^2）的算法和O(NlogN)算法性能上确实是差了很多，包括优化后的排序算法也比优化前的性能好了很多，故在某些场景下，选择合适的排序算法才是成功之道。