动规解决的问题:
重复子问题;
动规与贪心的区别:
贪心是局部选优,不涉及到状态迁移问题;
动规写法:
动规分为普通动规以及背包问题,写法皆为 动规五部曲:
首先,明确动规数组含义;
其次,明确递推公式;
然后,确定初始化;
再者,确定遍历顺序;
最后,出错打印数组;
举例:
1.? 爬楼梯消费体力问题:leetcode 746
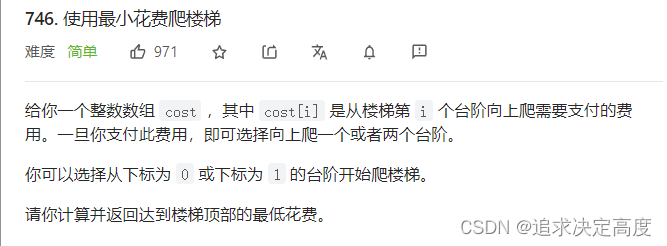
?思路:
重复子问题:每次爬楼梯都是 一层或者两层--->选择动规;
五部曲:
dp[i] 含义:爬到下标为 i 层的楼梯需要的最小花费;
规定 :
爬到某一层时需要花费该层的体力。
离开该层不花费体力。
爬到顶层,顶层不花费体力
注意区别:问题是询问爬到楼顶的花费,我们设的是爬到某层楼梯的花费!!
递推公式:如果爬到下标为2的楼梯,根据 每次 爬? 1 / 2 层可知,可以从0 爬两层到2,也可以从1爬1层到2;即:
dp[2]=min(dp[0],dp[1])+cost[2];
则,爬到顶层,即 下标为 2 楼梯的 下一层【楼梯总数为3】,最低花费可以是:
min(dp[2],dp[1])
初始化:dp[0]=cost[0] , dp[1]=cost[1];
遍历顺序:从前往后
打印数组:略
代码:
class Solution { public: int minCostClimbingStairs(vector<int>& cost) { vector<int> dp(cost.size()); dp[0] = cost[0]; dp[1] = cost[1]; for (int i = 2; i < cost.size(); i++) { dp[i] = min(dp[i - 1], dp[i - 2]) + cost[i]; } // 注意最后一步可以理解为不用花费,所以取倒数第一步,第二步的最少值 return min(dp[cost.size() - 1], dp[cost.size() - 2]); } };
2.? 机器人路径问题 leetcode 62

??思路:
重复子问题:每次机器人都是往下走或者往右走--->选择动规;
五部曲:
dp[i][j]?含义:到达第【i,j】需要多少步;
注意:何时选择二维dp,一维dp,根据题目的要求,此题给了二维网格,显然用二维更好
递推公式:因为每次机器人走法,只能向右或者向下,则到达第 (i,j)处,只能通过左边或者上方走到,即:
dp[i][j]=dp[i-1][j]+dp[i][j-1];
初始化:dp[0][j]=1;dp[i][0]=1;
遍历顺序:从前往后
打印数组:略
?代码:
class?Solution?{
public:
????int?uniquePaths(int?m,?int?n)?{
????????vector<vector<int>>dp(m,vector<int>(n));
????????//dp[i][j]表示到达下标?(i,j)的路径数
????????//递推公式:dp[i][j]=dp[i-1][j]+dp[i][j-1];
????????//初始化:dp[0][j]=1,dp[i][0]=1;
????????//遍历顺序:从前往后;
????????//打印数组
????????for(int?i=0;i<m;i++)dp[i][0]=1;
????????for(int?j=0;j<n;j++)dp[0][j]=1;
????????for(int?i=1;i<m;i++){
????????????for(int?j=1;j<n;j++){
????????????????dp[i][j]=dp[i-1][j]+dp[i][j-1];
????????????}
????????}
????????return?dp[m-1][n-1];
????}
};
3. 机器人路径问题,有障碍 leetcode? 63
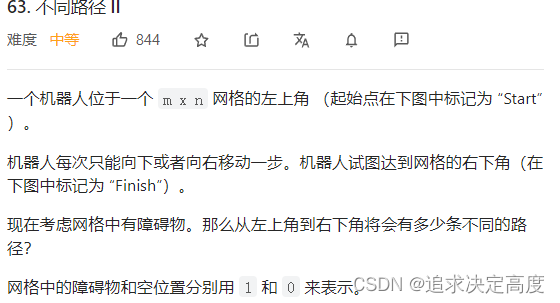
与上题不同在于,此题路径中有障碍:
如何考虑?
如果有障碍,则说明所有原本经过该位置【原来无障碍,现在有障碍】到达目的地的走法都不能够计入路径总数!
因此,我们将经过该路径时的dp值不更新即可!
代码:
class?Solution?{
public:
????int?uniquePathsWithObstacles(vector<vector<int>>&?obstacleGrid)?{
????????int?m=obstacleGrid.size();
????????int?n=obstacleGrid[0].size();
????????vector<vector<int>>dp(m,vector<int>(n));
????????//dp[i][j]表示到达下标?(i,j)的路径数
????????//递推公式:dp[i][j]=dp[i-1][j]+dp[i][j-1];
????????//初始化:dp[0][j]=1,dp[i][0]=1;
????????//遍历顺序:从前往后;
????????//打印数组
????????for(int?i=0;i<m&&obstacleGrid[i][0]==0;i++)dp[i][0]=1;
????????for(int?j=0;j<n&&obstacleGrid[0][j]==0;j++)dp[0][j]=1;
????????for(int?i=1;i<m;i++){
????????????for(int?j=1;j<n;j++){
????????????????if(obstacleGrid[i][j]==1)continue;
????????????????dp[i][j]=dp[i-1][j]+dp[i][j-1];
????????????}
????????}
????????return?dp[m-1][n-1];
????}
};
?