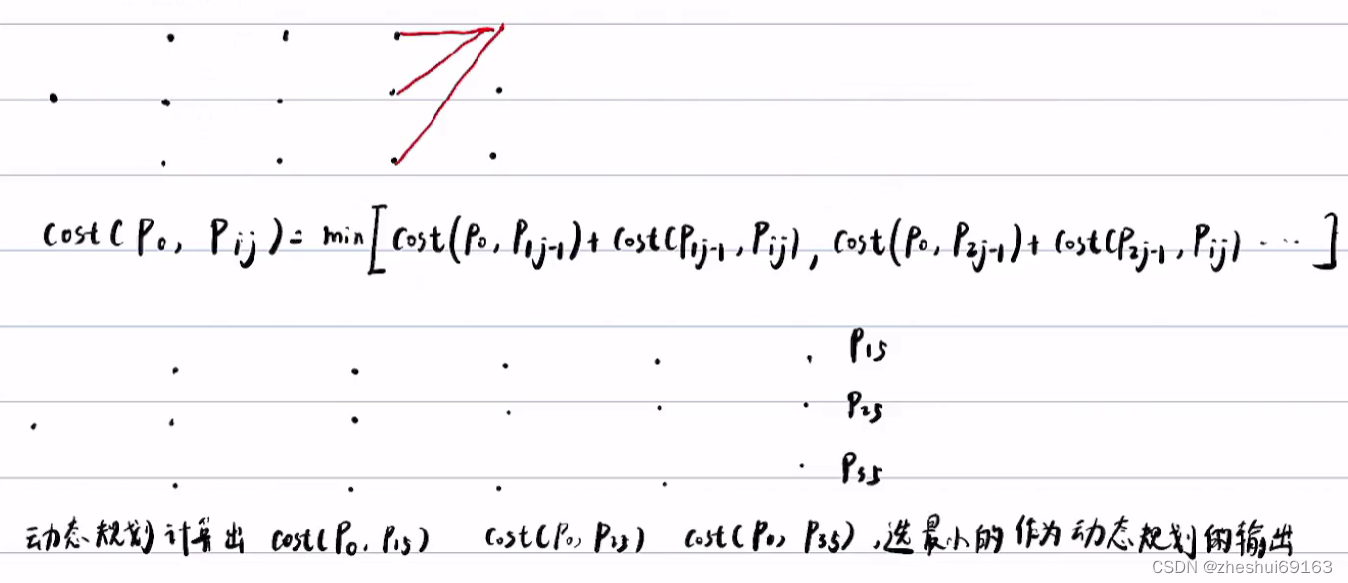这一节是根据参考线+障碍物实现避障的局部规划
这一节的理论,确定规划的起点是在frenet坐标系下的 哇塞每个规划周期下 这个参考线坐标都得换一次,这好烦呐; 撒点求粗解是在frenet坐标系下的, 而heading也是frenet坐标系下的,其实就是dl/ds,也就是l’ 也就是参考线的切线和s方向所成的夹角,最好不要理记为heading,不然容易和大地坐标系冲突
哇哇哇,再次验证规划和决策之间的关系:全局决策-全局规划,局部决策-局部规划
上一节:参考线,提供光滑的frenet坐标轴(参考线不是全局路径哈,是全局路径的优化,没那么长,且平滑,需要一直更新)
(这个意思是把参考线的xy坐标写出来了,方便以后建立参考线frenet坐标系,对于其他点参考参考线得到s-l坐标。 不是直接把参考线frenet坐标了啊,是frenet坐标轴!!!)而且一般xy坐标转frenet坐标也得先有参考线在xy下的(x,y,theta,kappa)才行,只是之前学坐标转换的时候默认这个值已经有了
现在以host在referenceline的投影为坐标原点,建立frenet坐标系
(终于要建立坐标系了!而且投影点终于发挥作用了(坐标原点),之前都没啥子用)
话说,这个原点是动态的吗?还是只是初始位置,还是每个规划周期的位置,还是每时每刻的位置?是每个规划周期内的,因为每个规划周期内的参考线都是变化的,初始点也都是重新确定的
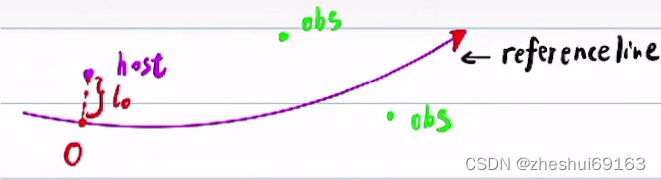
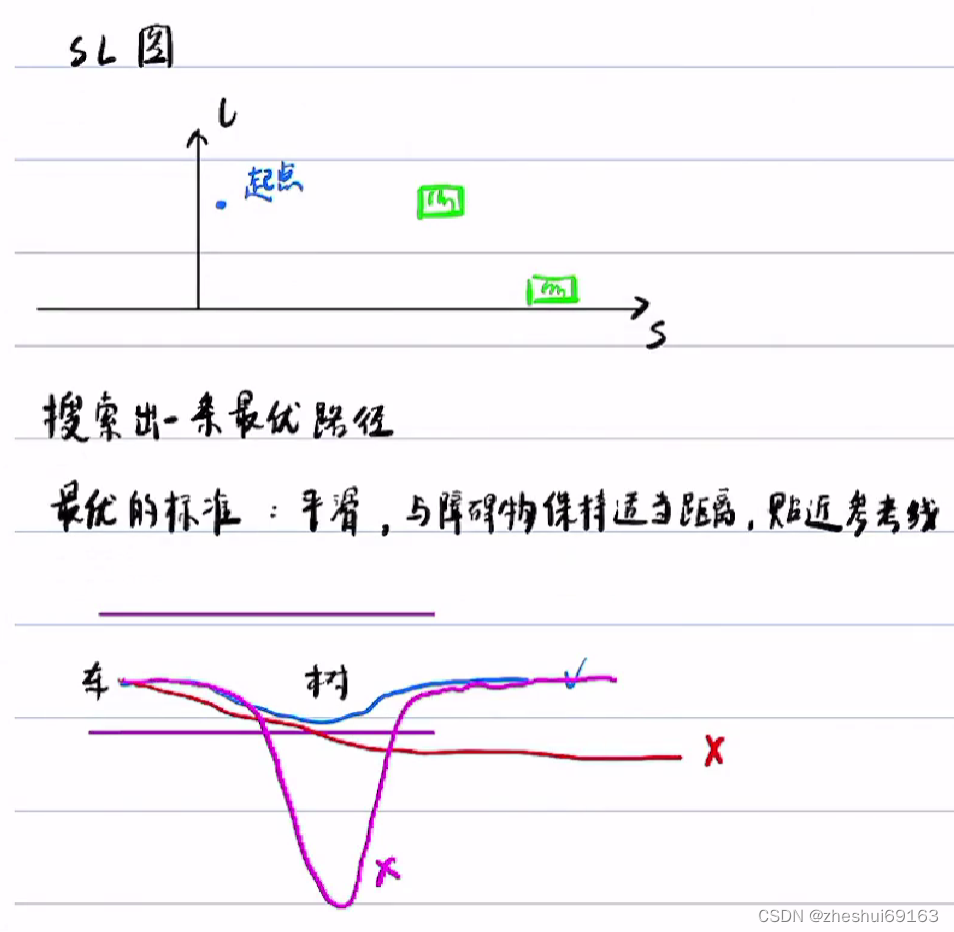
障碍物投影以生成SL图(这个的目的是为了后面避障)这里也有障碍物投影啊,为啥之前的参考线算法里面投影只考虑了一个点?因为前面是参考线模块,这里是避障模块
现在开始规划(因为有障碍物所以需要规划)
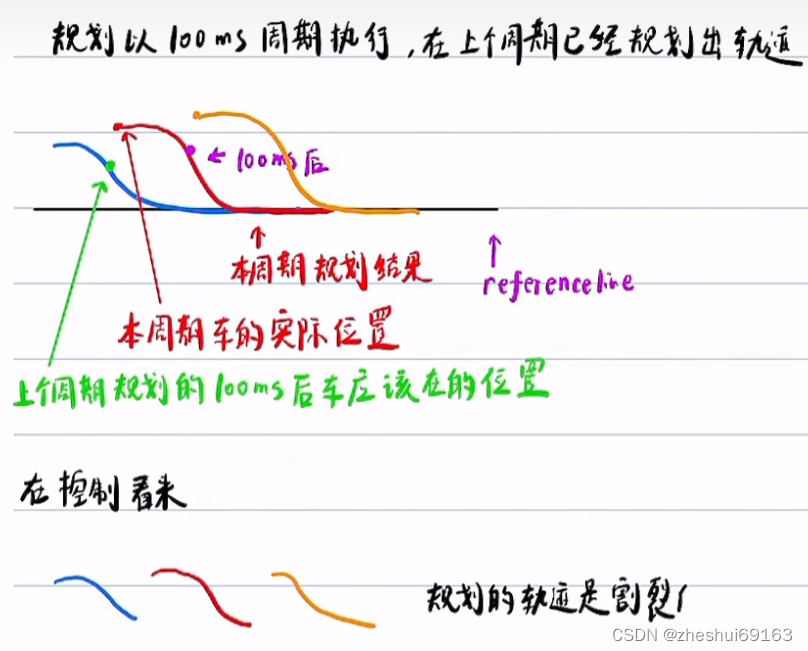
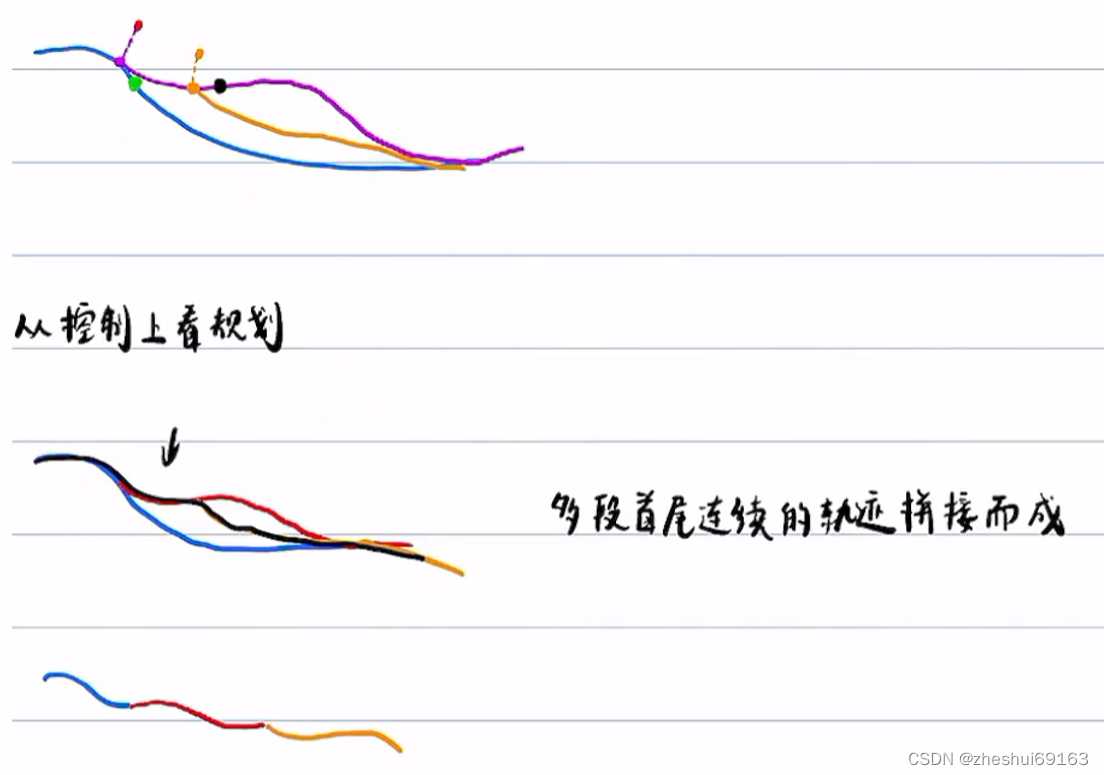
1.0确定规划的起点(错误思想):
车当前的实际位置是(0,l_0),但这不能作为规划的起点,因为控制是不完美的,上次规划的时候,规划处蓝色的轨迹,理论上按照这个轨迹走这个车应该在绿色点位置,但最后其实在红色点位置;若该周期规划的起点按实际红色位置作为起点规划出红色的曲线,依次类推【其实对于第一个周期,是可以这样干滴!】
会导致从上个周期-本周期-下周期下,整个规划出的轨迹是割裂的这会导致控制中期望的前轮转角发生突变,存在安全问题 emmm这个突变是因为 红点出的斜率和绿点不一样,给他搞一样不就行了?还是说只要割裂,即使斜率相等也不好吗?应该还得连续,不连续的话会怎么样?不连续目标位置就不一样啦,控制不就得网上靠,这个距离太远啦,靠起来不方便 为啥子红点处的新线要先平一段啊?应该是举例不平也行
1.1确定规划的起点(正确做法)
1.1.1若误差大,仍以当前实际位置做规划起点,
从这里也就能看出来坐标原点每次是根据每次规划周期的车的位置的,所以frenet坐标系是根据每规划周期内车的位置动态变化的
好奇啊,这样不也就还是轨迹不连续嘛?对啊,那没办法,只能这样,若不这样还按照原来的轨迹来,车跟轨迹很难的
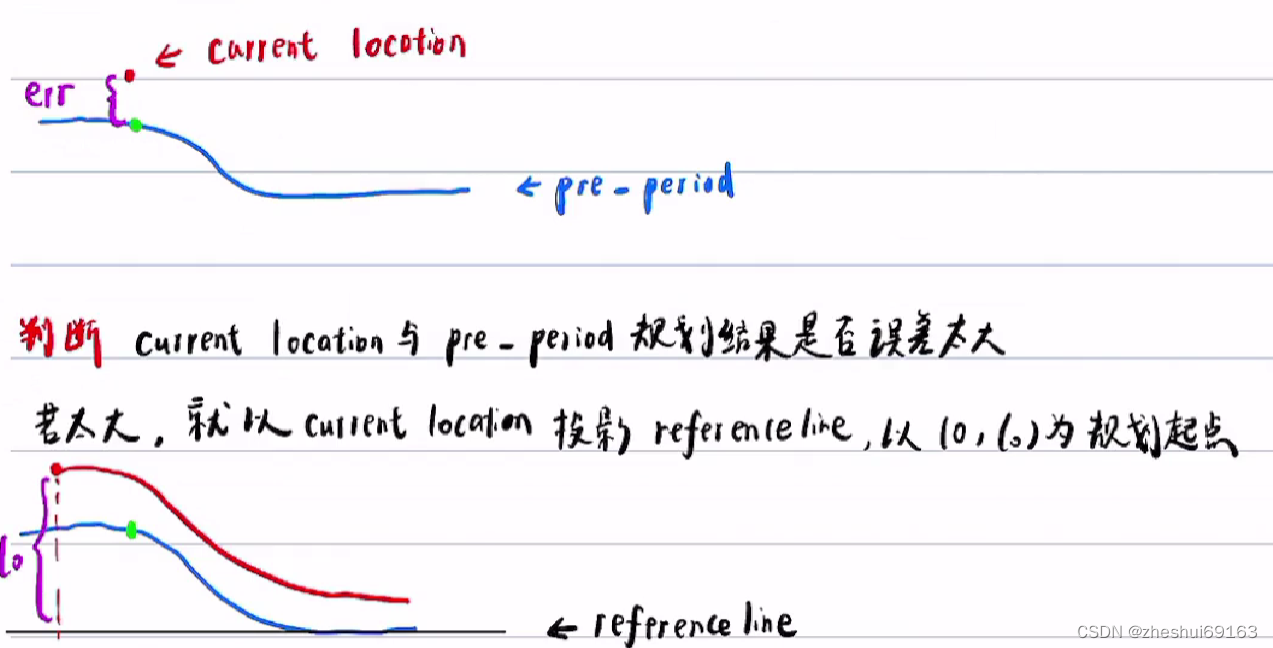
1.1.2若误差不大,法1:以当前实际位置投影至上个周期规划轨迹P(s_0,l_0); 法2:以 理论绿色点做规划起点

1.1.2.1 对于法1:生成的总体局部路径就是连续的(但不一定可导)
老王说:从 05:19 开始讲的规划起点的算法其实并不准确,正确的轨迹规划的起点算法应该按照第二章第三节(中)的方法!!!!!!!!!!!!因为上面这个这个规划起点是基于当前位置的,不是哈,应该是预估100ms后作为起点!!!
2. 确定完规划起点之后,我们来基于障碍物----规划轨迹
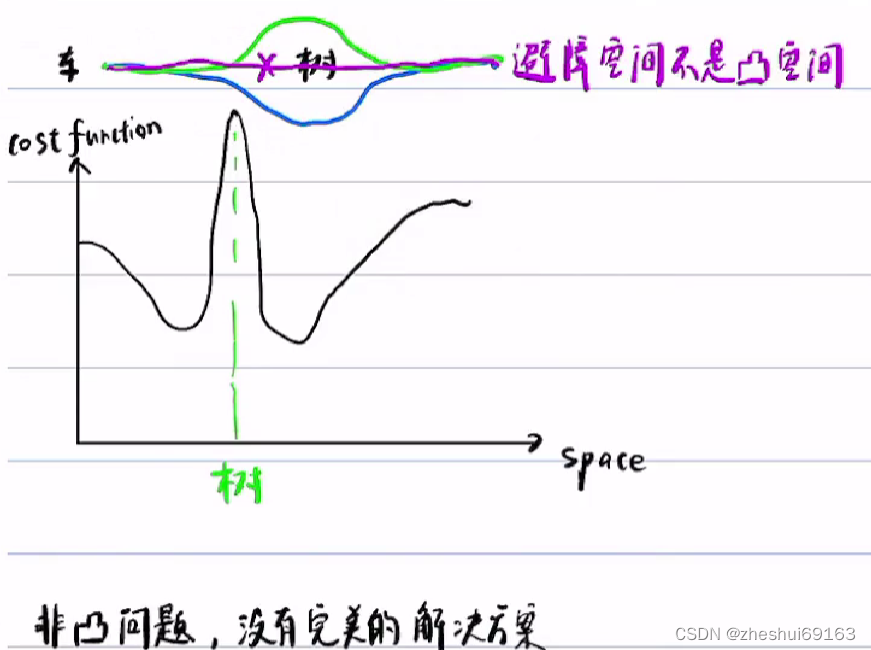
基于上述3个最优标准,可以用二次规划解决,但二次规划是非凸的。对于cost function 函数,当space在树的位置,损失是很大的,但在树的两侧均存在两个cost function的极小值。

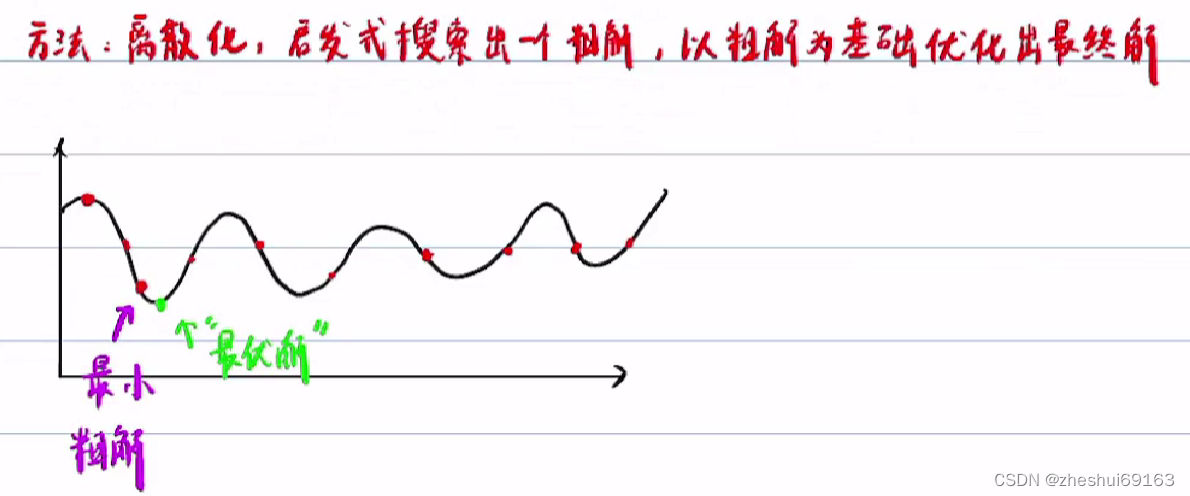
2.1解决方法:下面这种离散化,启发式搜索粗解,其实这个找粗解过程其实就是决策的过程
决策就是往左、右绕;选择往左/右的本质是选择左/右凸空间作为解空间;即:撒点选择到的粗解在左/右空间,粗解在哪个空间,就选择哪个空间作为最优凸空间
缺点:受到采样密度制约
2.2具体来说:
2.2.1 每隔纵向的一定距离,在横向上撒一些点,然后在离散空间中连线,找最优轨迹(cost function最小,即粗解,注意粗解不是点哈,是轨迹!!!)(在离散空间中的最优路径称为粗解)这个纵向是指l坐标轴
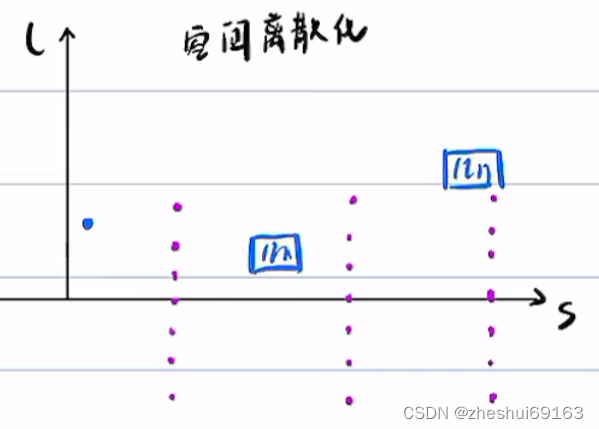

2.2.1 离散空间中找最优路径(cost function最小),此最优路径将开辟一个凸空间,再在此凸空间上做二次规划(离散空间的最优路径称为粗解,粗解开辟凸空间,在此凸空间上优化出最终解)我天这咋确定凸空间

如何在离散空间上找到粗解?动态规划(本节讲)
粗解怎么确定凸空间?
如何在凸空间上优化出最终解? 二次规划(下一节讲)
3、在离散空间上找到粗解–动态规划

如果离散取点的时候是纵轴方向 s坐标相等,那么就直接s1 s2等,不需要s11 s12了,对,是这样!
举例如下,原本推到五次多项式是根据时间来的,这里是根据位置来的,这里居然不是速度约束?而是航向角约束,这两个好像一回事哈,因为是一个方向上的,但之前推导好像是速度大小没有管方向哎(这两个不是一回事,但原理一样,之前是初末时间下位置、速度、加速度的限制,所以五次多项式;而这里是初末位置和斜率的约束,若考虑初末的二阶导也就是6个约束,所以也是五次多项式)
这里没有f’'=0,因为一般约束到f’就够了这里f‘’=0,安理来说,这里是不是随便等于一个值?反正没有约束,写也只是为了求解?下面老王也是这样说的,而且理论上 都等于0,也方便不同线段间的衔接了。 虽然说非起点的一阶导和所有点的二阶导直接=0,但这只是因为没有值可以赋,理论上可以赋其他值,但不代表可以没有这个约束,所以仅仅用一次函数是不行的
heading也是frenet坐标系下的,其实就是dl/ds,也就是l’ 也就是参考线的切线和s方向所成的夹角

上面是有初始点航向角约束的情况,若直接没有初始点就直接一阶导二阶导=0(因为这个解是粗解,他的最终目的是为了开辟凸空间,至于这个解长成什么样不重要,最终是为了在凸空间中求),如下:
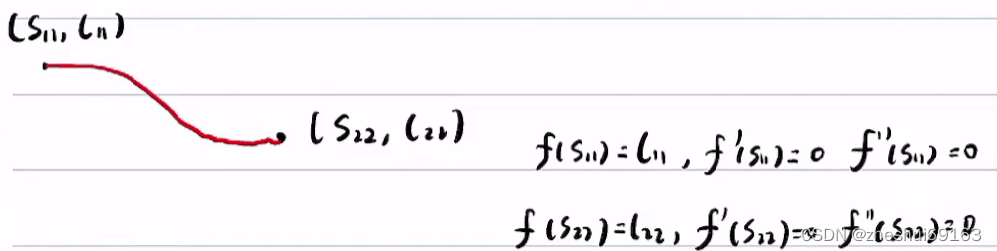
3.1 如何评价路径的优劣–cost function
之前由全局路径得参考线的评价指标:离散点的平滑、线段短、 原始轨迹距离近
这里 的评价指标:连续曲线平滑、障碍物距离、参考线距离近
对于平滑:因为规划出的全局路径是离散的点,所以他的表达是用向量搞,这里局部路径规划的是多段五次多项式,并且五次多项式之间是平滑的,因为导数都=0,所以直接求导就行。这只是算一个点这样来,多个点也是在连续曲线上离散取点求和
对于距离: ==之前考虑了线段长,为啥这里不用考虑????????==当然这里是肯定要考虑和障碍物的距离的。也是在连续曲线上离散取点求和
对于差值距离:之前是离散的点直接求差值和。这里是在连续曲线上取离散点,然后求差值和
前面搞五次多项式并不是为了让车跟踪曲线,车跟踪的本质上还是离散的点。 这里搞五次多项式只是为了后面密集取点的合理性。否则直接不连线直接求每个点的costfunction了,但这样不符合车的运动性质

下面是针对上面的解释,对于平滑,平滑也就是为了让线最短,也就是xxxx,最后也就是\sum f ’ ^2最小
障碍物距离函数g有多种形式,只要满足,小距离d2内代价无限大,远距离d1外代价为0,一定范围d2~d1内,代价随着距离的减小而增大,整体就是一个减函数嘛,可以画图感受下

每个路径都有对应的cost,问题就变成找图的最短路径的问题(因为每一段都是独立的,感觉第一段取min往后都是这样,不就是dijkstra,对!但因为道路没这么麻烦,所以不用dijkstra也可以)
下面这个不就是遍历,只是从左往右每一层都取min算,这样可以实现把复杂问题分成简单问题【这就是动态规划,每次只考虑局部,得到的值再传到下一层】