文章目录
基本思想
每步将一个待排序的对象,按其关键码大小,插入到前面已经排好序的一组对象的适当位置上,直到对象全部插入位置。
即边插入边排序,保证子序列中随时都是排好序的。
基本操作:有序插入
- 在有序序列中插入一个元素,保持序列有序,有序长度不断增加。
- 起初,a[0]是长度为1的子序列。然后,逐一将a[1]至a[n-1]插入到有序子序列中。
有序插入方法:
① 在插入a[i]前,数组a的前半段(a[0] - a[i-1])是有序段,后半段(a[i] - a[n-1])是停留于输入次序的“无序段”。
② 插入a[i]使a[0] - a[i-1] 有序,也就是要为a[i]找到有序位置j(0≤ j ≤ i),将a[i]插入在a[j]的位置上。
插入图示
如何找到插入位置 j 呢?
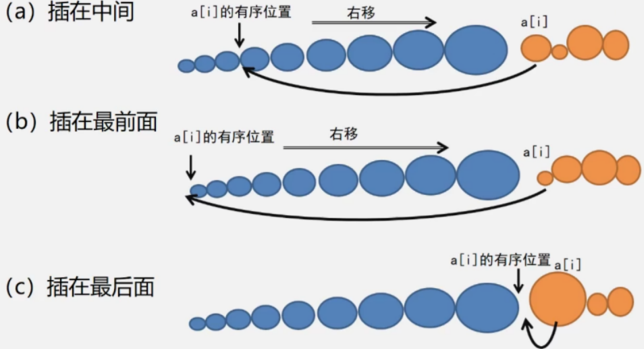
插入排序的种类
顺序法定位插入位置——直接插入排序
二分法定位插入位置——二分插入排序
缩小增量多遍插入排序——希尔排序
直接插入排序
直接插入排序——采用顺序查找法查找插入位置。
排序过程
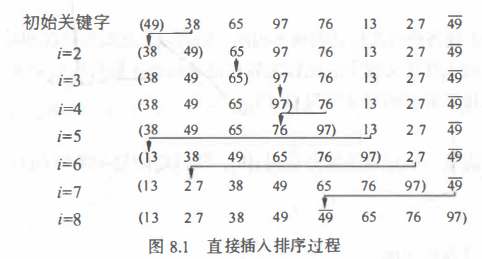
1.复制插入元素
x = a[i];
2.记录后移,查找插入位置
for(j=i-1;j>=0&&x<a[j];j--)
a[j+1]=a[j];
3.插入到正确位置
a[j-1]=x;
具体实现
void InsertSort(SqList &L)
{ //对顺序表L做直接插入排序
for(i=2;i<=L.length;++i)
if(L.r[i].key<L.r[i-1].key) // “<”,需将r[i]插入有序子表
{
L.r[O]=L.r[i]; // 将待插人的记录暂存到监视哨中
L.r[i]=L.r[i-1]; // r[i-1]后移
for(j=i-2; L.r[O].key<L.r[j].key; --j) // 从后向前寻找插入位置
L.r[j+1]=L.r[j]; // 记录逐个后移,直到找到插入位置
L.r[j+1]=L.r[O]; // 将 r[O]即原r[i],插人到正确位置
}
}
//if
插入排序性能分析
实现排序的基本操作有两个:
(1)“比较”序列中两个关键字的大小;
(2)“移动”记录。
最好的情况(关键字在记录序列中顺序有序):
11 25 32 47 56 70 81 85 92 96

最坏的情况(关键字在记录序列中逆序有序):
81 85 92 96 70 56 47 32 25 11
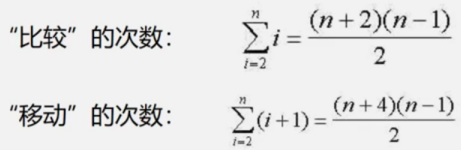
平均情况:
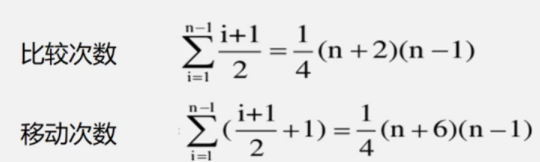
时间复杂度结论
- 原始数据越接近有序,排序速度越快
- 最坏情况下(输入数据是逆有序的)Tw(n) = O(n2)
- 平均情况下,耗时差不多是最坏情况的一半 Te(n) = O(n2)
- 要提高查找速度,就要减少元素的比较次数、减少元素的移动次数
折半插入排序
查找插入位置时采用折半查找法。
具体实现
void BinsertSort(SqList &L)
{ // 对顺序表L做折半插入排序
for (i=2; i < =L.length; ++i)
{
L.r[O]=L.r[i]; // 将待插人的记录暂存到监视哨中
low=1;high=i-1; // 置查找区间初值
while(low<=high) // 在r[low .. high]中折半查找插入的位置
{
m=(low+high)/2; // 折半
if(L.r[O].key<L.r[m].key) high=m-1; // 插入点在前一子表
else low=m+1; // 插入点在后一子表
}
for (j=i-1;j>=high+1; --j) L.r[j+1]=L.r[j]; //记录后移
L.r[high+1]=L.r[O]; // 将r[O]即原r[i], 插入到正确位置
} // for
}
折半插入排序算法分析
- 折半查找比顺序查找快,所以折半插入排序就平均性能来说比直接插入排序要快;
- 它所需要的关键码比较次数与待排序对象序列的初始排序无关,仅依赖于对象个数。在插入第i个对象时,需要经过log2i +1次关键码比较,才能确定它应插入的位置;
- 当n较大时,总关键码比较次数比直接插入排序的最坏情况要好得多,但比其好情况要差;
- 在对象的初始排列已经按关键码排好序或接近有序时,直接插入排序比折半插入排序执行的关键码比较次数要少;
- 折半插入排序的对象移动次数与直接插入排序相同,依赖于对象的初始排列
- 减少了比较次数,但没有减少移动次数
- 平均性能优于直接插入排序
时间复杂度为O(n2)
空间复杂度为O(1)
是一种稳定的排序方法
希尔排序(Donald.L.Shell)
直接、折半插入排序的思考
可以在直接、折半插入排序时增大移动的步幅吗?
由原来的比较一次移动一步,变成比较一次移动一大步?
直接插入排序, 当待排序的记录个数较少且待排序序列的关键字基本有序时,效率较高。希尔排序基于以上两点,从 “减少记录个数” 和 “序列基本有序” 两个方面对直接插入排序进行了改进。
希尔排序基本思想
先将整个待排记录序列分割成若干子序列,分别进行直接插入排序,待整个序列中的记录“基本有序”时,再对全体记录进行一次直接插入排序。
希尔排序算法特点
(1)缩小增量
(2)多遍插入排序
- 一次移动,移动位置较大,跳跃式地接近排序后的最终位置
- 最后一次只需要少量移动
- 增量序列必须是递减的,最后一个必须是1
- 增量序列应该是互质的
希尔排序过程
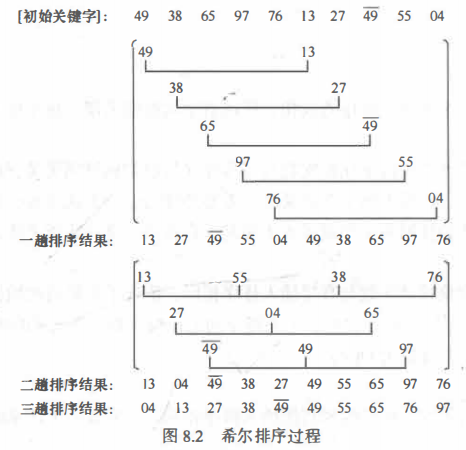
具体实现
void ShellInsert(SqList &L, int dk)
{ // 对顺序表L做一趟增量是dk的希尔插入排序
for(i=dk+1;i<=L.length;++i)
if(L.r[i].key<L.r[i-dk].key) // 需将L.r[i]插入有序增扯子表
{
L.r[O]=L.r[i]; // 暂存在L.r[O]
for(j=i-dk; j >O&& L.r[O].key<L.r[j].key;j-=dk)
L.r[j+dk]=L.r[j]; // 记录后移, 直到找到插入位置
L.r[j+dk]=L.r[O]; // 将 r[O]即原r[i], 插入到正确位置
}
}
void ShellSort(SqList &L,int dt[],int t)
{ //按增批序列 dt[O .. t-1]对顺序表 L作t 趟希尔排序
for (k=O;k<t;++k)
ShellInsert(L,dt[k]); // 一趟增址为 dt[t]的希尔插入排序
}
希尔排序算法分析
希尔排序算法效率与增量序列的取值有关

时间复杂度是n和d的函数:
O(n1.25) - O(1.6n1.25) ——经验公式
空间复杂度为O(1)
是一种不稳定的排序方法
如何选择最佳d序列,目前尚未解决;
最后一个增量值必须为1,无除了1之外的公因子;
不宜在链式存储结构上实现。
希尔排序算法特点
(1) 记录跳跃式地移动导致排序方法是不稳定的。
(2) 只能用于顺序结构,不能用于链式结构。
(3) 增量序列可以有各种取法,但应该使增量序列中的值没有除1 之外的公因子,并且最后一个增量值必须等于1。
(4) 记录总的比较次数和移动次数都比直接插入排序要少,n越大时,效果越明显。所以适合初始记录无序、n较大时的情况。