算法描述
将输入数组建立为一个 大顶堆,之后反复取出堆顶并对剩余元素重建大顶堆,将依次取出的堆顶逆序排列,即可将原数组从小到大排列完成排序。
一个直接的想法是在原数组之外新建一个数组保存每次取得的堆顶,这样会有 O(n)O(n) 的空间开销,可以用一种称作 **「原地堆排序」**的技巧避免此开销,具体做法如下。
首先将原待排序数组arr[]建立为一个大顶堆 (heapify堆化方法)。
交换堆顶和当前未排序部分中最末尾元素,则堆顶元素已排序(此时在数组最末尾)。
剩余元素中 只有当前堆顶(之前被交换的末尾元素)可能造成 堆失序,因此只需对堆顶调用一次调整堆序的下滤(siftDown)操作(操作范围为未排序部分),即可恢复未排序部分的堆序。
重复2,3直到所有元素已排序,返回arr[]。
上述通过交换堆顶与当前未排序部分末尾元素的做法,避免了额外的空间开销,即 原地堆排序,程序结束后返回的arr[]为已排序状态。
- 稳定性:不稳定。
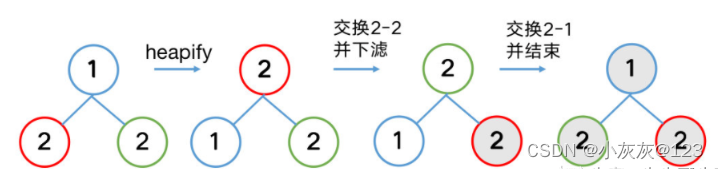
交换可能会破坏稳定性。例:输入数组 {1, 2, 2},变灰表示已排序。可以看到红2和绿2的相对顺序相比输入已改变。
- 堆化方法 (heapify)
将原输入数组看作一棵 完全二叉树(Complete Binary Tree)。根节点下标为0,于是根据完全二叉树的结构性质,任意一个节点(下标为 i )的左子节点下标为 2 * i + 12?i+1,右子节点下标为 2 * i + 22?i+2,父节点下标为 i / 2i/2。 堆化过程即使得整棵树满足堆序性质,也即任意一个节点大于等于其子节点(大顶堆)。堆化操作总结为一句话就是:对最后一个非叶子节点到根节点,依次执行下滤操作(siftDown)。
从最后非一个叶子开始下滤的原因是此节点之后的节点均为叶子节点,叶子节点无子节点,故其本身已满足堆序性质,也就无下滤的必要(也无法下滤)。每一次下滤使得该节点及其之后的节点都满足堆序性质,直到根节点。
※ 最后一个非叶子节点(也即最后一个元素的父节点)下标为 (n - 1) / 2(n?1)/2,n为数组长度。
如下动图是将输入数组{4, 6, 2, 1, 7, 9, 5, 8, 3} (1为最后一个非叶子结点) 堆化成大顶堆{9, 8, 5, 6, 7, 2, 4, 1, 3}的过程。
- 下滤方法(siftDown)
下滤(siftDown)是堆排序的核心方法,在堆排序中用于在程序开始时 创建大顶堆,以及在每次排序堆顶时用于 恢复未排序部分的堆序。
该方法来源于删除堆顶元素操作,先介绍下滤在删除堆顶元素操作中的处理过程。如下动图展示了删除大顶堆{9, 8, 5, 6, 7, 2, 4, 1, 3}堆顶元素9的过程(动图中出现的100表示堆顶,值为9)。
删除堆顶,堆中元素减1,将当前最后一个元素3暂时置为堆顶。
可以看到,此时影响堆序的只有该堆顶元素3,于是交换其与左右子节点中的较大者。
对元素3重复操作2,直到3再无子节点,堆序恢复。
恢复堆序的过程就是将影响堆序的元素不断向下层移动(并交换)的过程,因此形象地称之为下滤(siftDown)。
※ 注意,此处沿用JDK源码中下滤操作的方法名"siftDown",sift为过滤之意,网上有的博客文章将其讹误成shift。
可以看到,对节点x的下滤操作的本质是恢复以x为根节点的树的堆序。因此在堆化操作中,只需要分别依次地对最后一个非叶子节点到根节点执行下滤操作,即可使整棵树满足堆序。在排序过程中,每次原地交换后(交换当前堆顶与当前未排序部分最后一个元素),只有新堆顶影响堆序,对其执行 一次 下滤操作(范围为未排序部分)即可使未排序部分重新满足堆序。
- 复杂度分析
- 时间复杂度:原地堆排序的时间复杂度为 O(nlogn)O(nlogn)。
- 建堆时间复杂度: O(n)O(n),证明如下。

代码
public int[] heapSort(int[] arr) {
if (arr.length < 2) return arr;
heapify(arr, arr.length - 1); // 构建大顶堆
for (int i = arr.length - 1; i > 0; i--) { // i > 0即可,无需写成i >= 0,当n - 1个元素排序时,最后一个元素也已排序
swap(arr, 0, i); // 交换堆顶和当前未排序部分最后一个元素
// 此时除当前堆顶元素外都是保持堆序的,只需要对该堆顶调用一次下滤操作
siftDown(arr, 0, i - 1); // i - 1是未排序部分最后一个元素下标,确保下滤不会超过此范围
}
return arr;
}
private void heapify(int[] arr, int endIdx) {
for (int hole = (endIdx - 1) / 2; hole >= 0; hole--) { // (endIdx - 1) / 2伪最后一个非叶子节点下标
siftDown(arr, hole, endIdx);
}
}
private void siftDown(int[] arr, int hole, int endIdx) {
int target = arr[hole]; // target是要下滤的节点
int child = hole * 2 + 1;
while(child <= endIdx) {
// 满足第一个条件child < endIdx表示hole有右孩子,不满足则hole无右孩子,跳过
// 第二个条件arr[child + 1] > arr[child]只在第一个条件成立前提下进行判断(因此不必担心arr[child + 1]越界),
// 若满足,表示hole有右孩子且右孩子更大,令child为右孩子下标。
// 因此此if过后使得child是hole的孩子中较大的那个
if (child < endIdx && arr[child + 1] > arr[child]) {
child++;
}
// 若child大于target,则child上移到当前hole,hole下滤到child位置
if (arr[child] > target) {
arr[hole] = arr[child];
hole = child;
child = hole * 2 + 1; // 当然也可以写成child = child * 2 + 1
} else break; // 若无需交换hole与child,说明hole已经满足堆序(无需/无法再下滤),退出while
}
arr[hole] = target; // 将target填入hole中
}