[数据结构与算法]力扣周赛304 6135. 图中的最长环 内向基环树

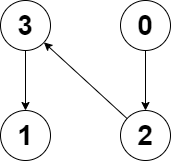
6135. 图中的最长环

给你一个?n?个节点的?有向图?，节点编号为?0?到?n - 1?，其中每个节点?至多?有一条出边。

图用一个大小为?n?下标从?0?开始的数组?edges?表示，节点?i?到节点?edges[i]?之间有一条有向边。如果节点?i?没有出边，那么?edges[i] == -1?。

请你返回图中的?最长?环，如果没有任何环，请返回?-1?。

一个环指的是起点和终点是?同一个?节点的路径。

示例 1：

输入：edges = [3,3,4,2,3]
输出去：3
解释：图中的最长环是：2 -> 4 -> 3 -> 2 。
这个环的长度为 3 ，所以返回 3 。

示例 2：

输入：edges = [2,-1,3,1]
输出：-1
解释：图中没有任何环。

提示：

• n == edges.length
• 2 <= n <= 1e5
• -1 <= edges[i] < n
• edges[i] != i

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/longest-cycle-in-a-graph
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

做题结果

周赛失败，晚上复盘一下子就写出来了T T。本来想问问大佬，然后试一下就出来了

方法：模拟

?

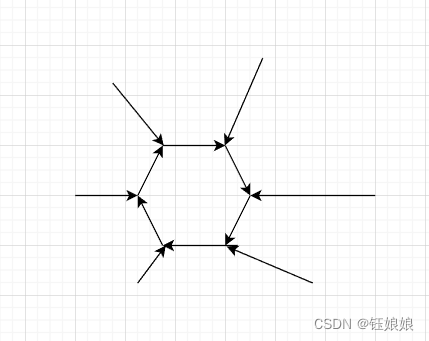
?单指针的图，最后都可以形成一个或多个类似上图的形状，多个外部线连到内部环

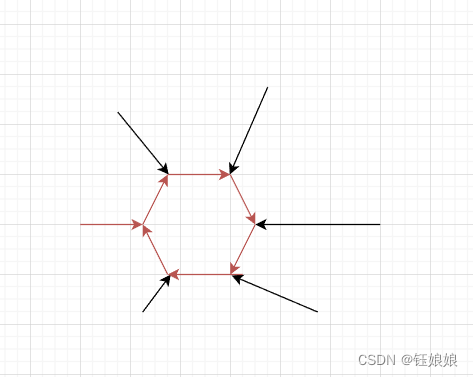
当我们从一个指针访问到重复节点的时候，可能得到上面红色线对应的结果，红色线对应的每个点都应该判重，打标记，后续在访问到红色位置访问过的节点时，直接结束

1. 访问到重复节点：记录当前时间戳和旧时间戳的差值结束，同时记录已访问点

2. 访问到非法节点（旧节点访问过的节点）：直接结束，记录已访问点

class Solution {
        public int longestCycle(int[] edges) {
            int n = edges.length;
            boolean[] visited = new boolean[n];
            int ans = -1;
            for(int i = 0; i < n; i++){
                if(visited[i]) continue;
                Map<Integer,Integer> used = new HashMap<>();
                int pos = i;
                int size = 0;
                while (edges[pos]!=-1&&!used.containsKey(edges[pos])&&!visited[edges[pos]]){
                    ++size;
                    pos = edges[pos];
                    used.put(pos,size);
                }
                if(edges[pos]!=-1&&!visited[edges[pos]]){
                    ans = Math.max(ans,size-used.get(edges[pos])+1);
                }
                for(Integer key:used.keySet()){
                    visited[key]=true;
                }
            }
            return ans;
        }
    }

?