6.4 堆排序算法
1、如何实现堆排序?
(1)观察:BUILD-MAX-HEAP将输入数组A[1…n]建成最大堆,其中n=A.length,根结点A[1]必定是最大的元素。
(2)过程:我们只要将A[1]和A[n]互换,然后将A[n]排出这棵树(通过n–来实现),再将剩余元素组成的新的树通过MAX-HEAPIFY重新构建成一个最大堆。
(3)后续:不断(2)过程即可。
2、伪代码
HEAPSORT(A)
1 BUILD-MAX-HEAP(A) //将数组转换为最大堆
2 for i = A.length downto 2
3 exchange A[1] with A[i] //将A[1]和A[i]交换
4 A.heap-size = A.heap-size - 1 //减小A.heap-size
5 MAX-HEAPIFY(A,1) //调用该函数使剩余元素依旧组成最大堆
3、案例
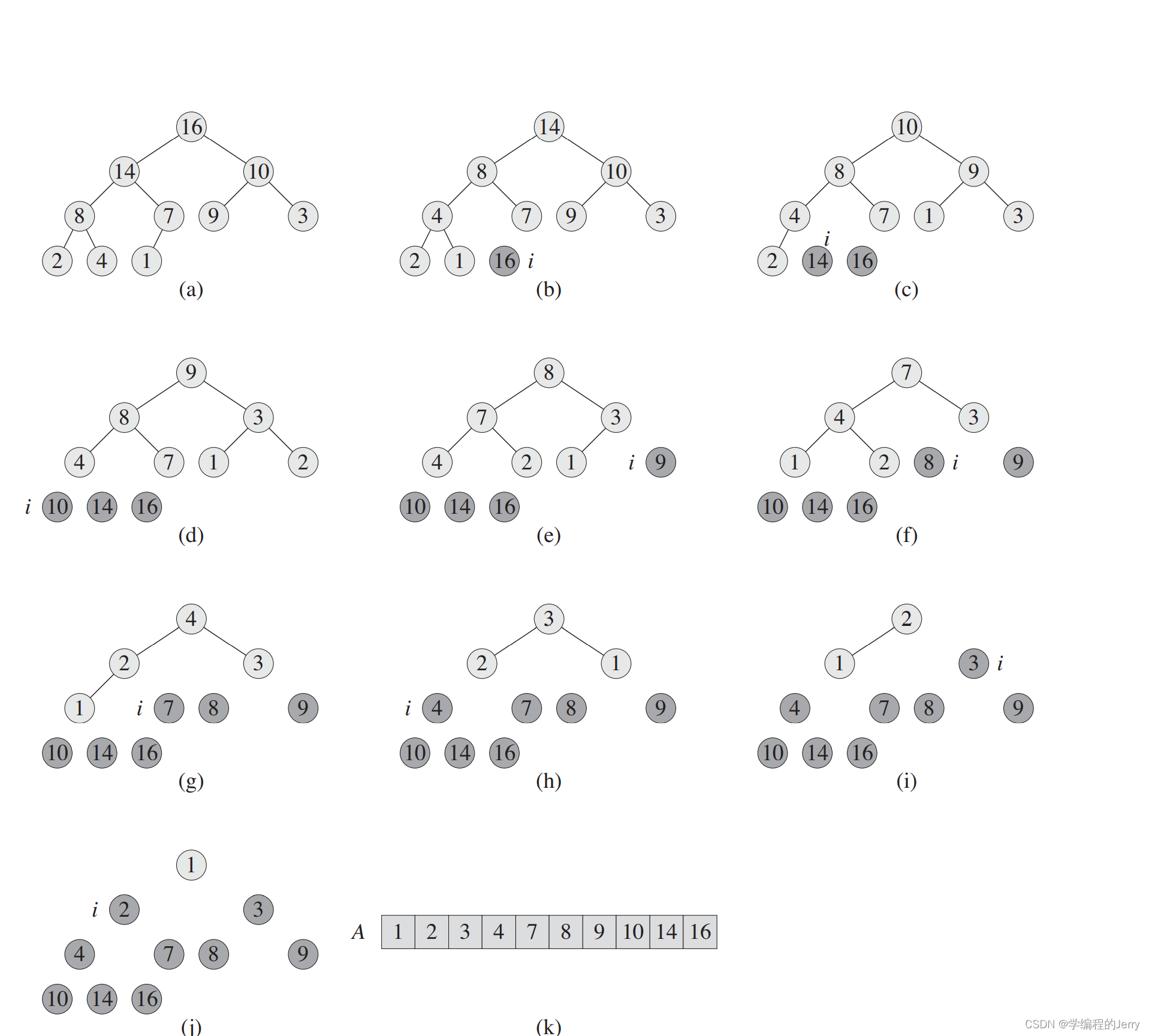
图1 描述了HEAPSORT(A)的工作过程:
(a)执行第一行BUILD-MAX-HEAP(A),产生一个最大堆。
(b)~(j)每次执行后续几行,将最大的数字(黑色阴影)排出,并将剩余部分(浅色阴影)重新整合为最大堆,标识当前的i。
(k)最终数组A的排序结果。
6.5 优先队列
一、引入
这里介绍堆的一个常见的应用:作为优先队列。
二、概念相关
1、概念:优先队列是一种用来维护由一组元素构成的集合S的数据结构,其中每一个元素都有一个相关的值,称为关键字。
2、一个最大优先队列支持的操作:
(1)INSERT(S,X):把元素X插入到集合S中。
(2)MAXIMUM(S):返回S中具有最大关键字的元素。
(3)EXTRACT-MAX(S):去掉并返回S中的具有最大关键字的元素。
INCREASE-KEY(S,x,k):把元素x的关键字值增加到k,这里假设k的值不小于x的关键字值。
最小优先队列则类似
三、案例
1、通过HEAP-MAXIMUM来实现MAXIMUM操作,在θ(1)的时间内。
HEAP-MAXIMUM(A)
1 return A[1]
2、通过HEAP-EXTRACT-MAX实现EXTRACT-MAX操作:
HEAP-EXTRACT-MAX
1 if A.heap-size < 1 //验证队列里是否还有元素
2 error "heap underflow"
3 max = A[1] //引入变量max记录A[1]的值
4 A[1] = A[A.heap-size] //将A[n]赋值给A[1]
5 A.heap-size = A.heap-size - 1 //将n--
6 MAX-HEAPIFY(A,1) //将剩余部分恢复为最大堆
7 return max //返回最大值
这个过程时间复杂度为O(lg n),因为除了时间复杂度为O(lg n)的MAX-HEAPIFY操作之外,其他操作都只需花常数阶的时间。
3、通过HEAP-INCREASE-KEY实现INCREASE-KEY操作:
(1)伪代码:
HEAP-INCREASE-KEY(A,i,key)
1 if key < A[i] //判断key是否小于A[i],小于就没法进行INCREASE操作
2 error "new key is smaller than current key"
3 A[i] = key
//如果A[i]大于父结点,那么就要将其与父结点交换值以满足最大堆性质
4 while i > 1 and A[PARENT(i)] < A[i]
5 exchange A[i] with A[PARENT(i)]
6 i = PARENT(i)
这个过程的时间复杂度为O(lg n),因为在算法第3~6行中类似MAX-HEPIFY的操作需要该时间。
(2)案例:
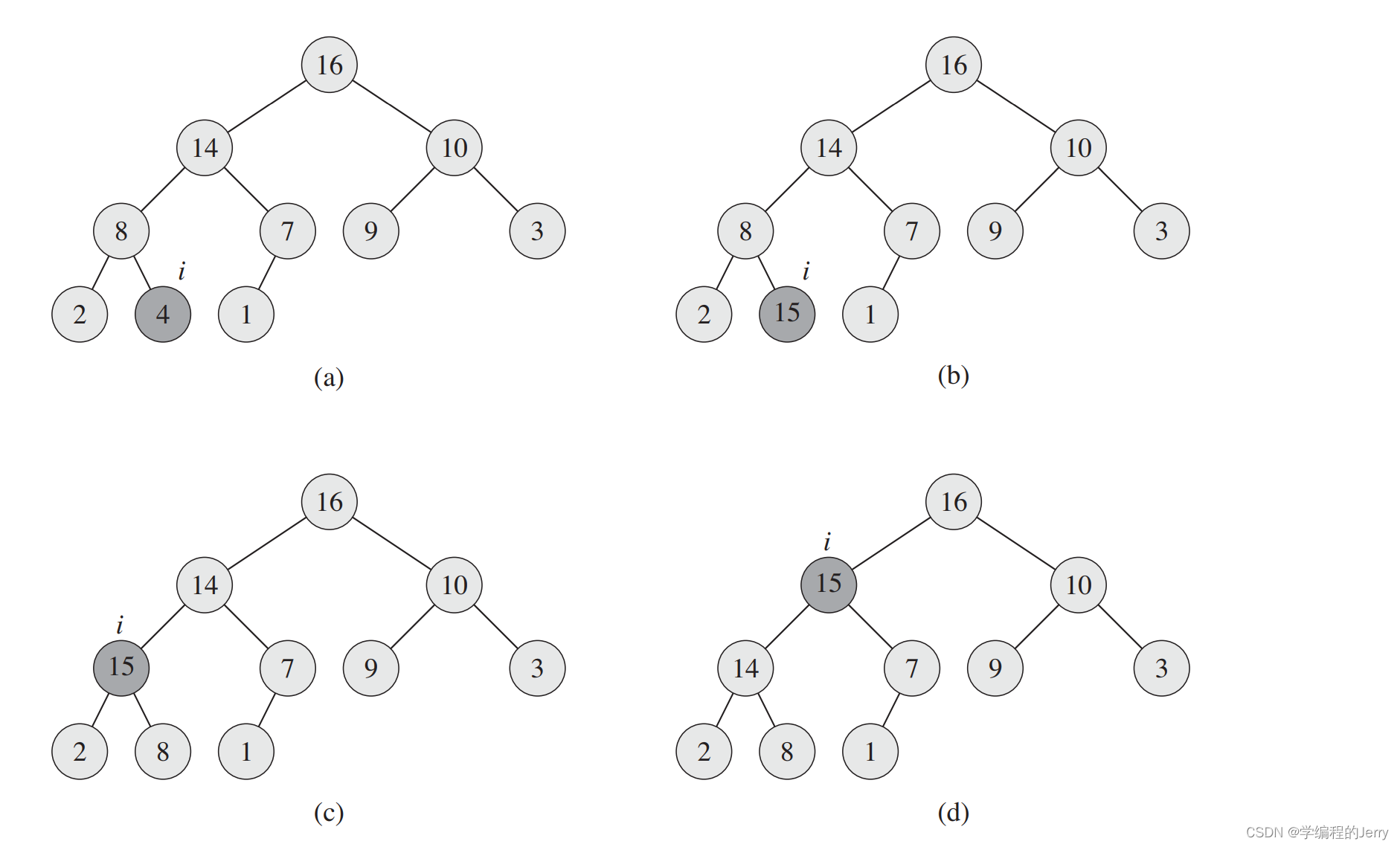
(a)图中为最大堆,下标i结点用深色阴影显示。
(b)将该关键字增加到15。
(c)经过一次4~6行的迭代,i与父结点交换位置。
(d)经过再一次迭代,使得整棵树满足最大堆性质,程序结束。
4、通过MAX-HEAP-INSERT实现INSERT操作
MAX-HEAP-INSERT(A,key)
1 A.heap-size = A.heap-size + 1 //增加一个-∞的叶结点来扩大最大堆
2 A[A.heap-size] = -∞
//通过调用HEAP-INCREASE-KEY来为新结点设置对应的关键字,同时保持最大堆的性质
3 HEAP-INCREASE-KEY(A,A.heap-size,key)
在包含n个元素的堆上,MAX-HEAP-INSERT的运行时间为O(lg n)。