leetcode-952:按公因数计算最大组件大小
题目
题目连接
给定一个由不同正整数的组成的非空数组 nums ,考虑下面的图:
有 nums.length 个节点,按从 nums[0] 到 nums[nums.length - 1] 标记;
只有当 nums[i] 和 nums[j] 共用一个大于 1 的公因数时,nums[i] 和 nums[j]之间才有一条边。
返回 图中最大连通组件的大小 。
示例 1:

输入:nums = [4,6,15,35]
输出:4
示例 2:

输入:nums = [20,50,9,63]
输出:2
示例 3:
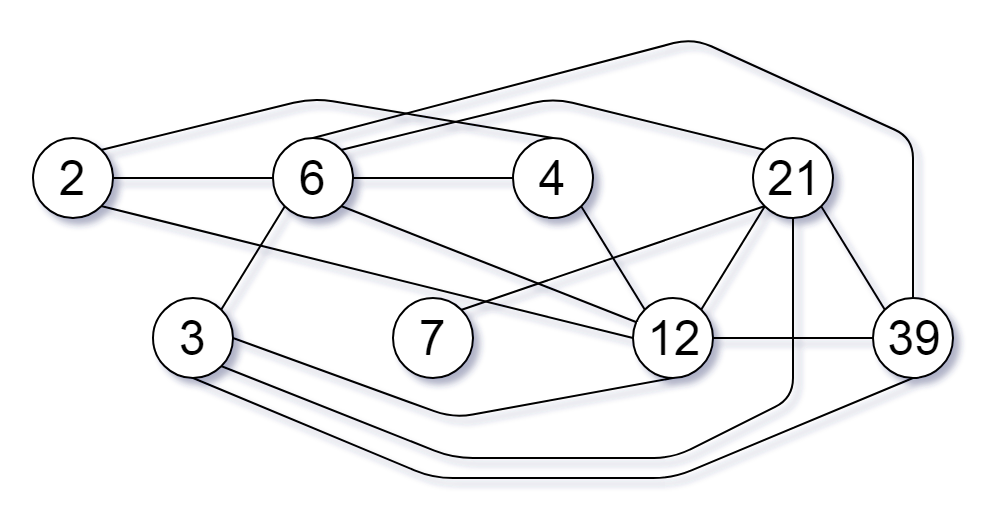
输入:nums = [2,3,6,7,4,12,21,39]
输出:8
解题
方法一:带权重有向图+并查集(超时)
带权重的图+并查集
写法一:
每个节点还带了权重weight[i],表示直接指向当前节点的 节点个数
最后只需要找到权重最大的,就是我们想要的答案。
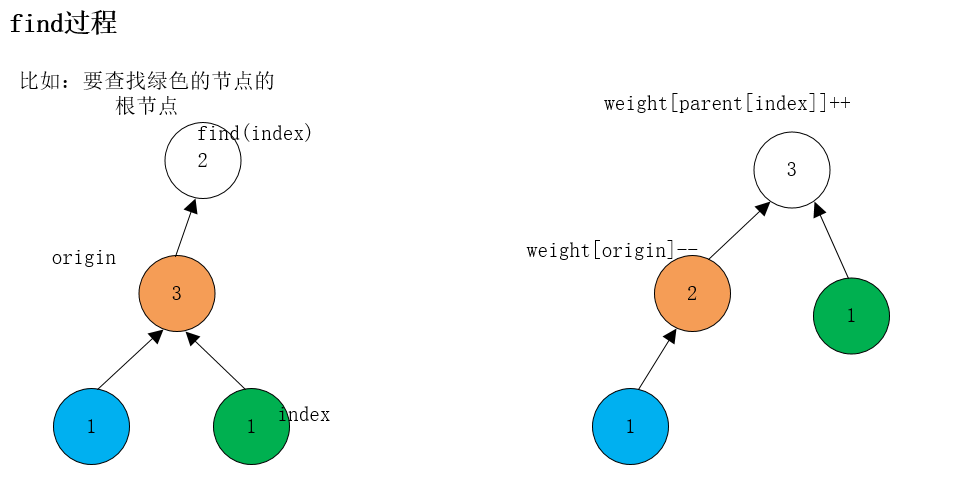
能直接遍历weight来获得最大的集合元素个数?显然不能直接这么做,还需要对他进行路径压缩,让元素直接指向根节点。
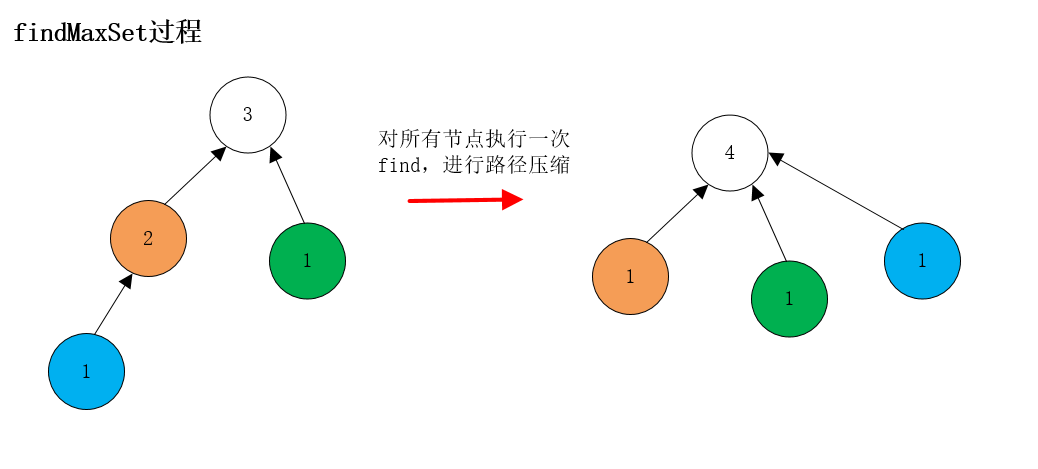
class UnionFind{
private:
vector<int> parent;
vector<int> weight;
public:
UnionFind(int n){
parent.resize(n);
weight.resize(n);
for(int i=0;i<n;i++){
parent[i]=i;
weight[i]=1;//直接指向当前节点的数量(包含自身,注意孙子节点,不算直接指向)
}
}
int find(int index){
if(parent[index]==index) return index;
int origin=parent[index];
parent[index]=find(parent[index]);
weight[parent[index]]++;//指向根节点的节点数量+1
weight[origin]--;//指向原先节点的节点数量-1
return parent[index];
}
void unite(int index1,int index2){
int p1=find(index1);
int p2=find(index2);
if(p1!=p2){
parent[p1]=p2;
weight[p2]++;//指向根节点的节点数量+1
}
}
int findMaxSet(){
for(int i=0;i<weight.size();i++){
find(i);
}
int res=0;
for(int i=0;i<weight.size();i++){
res=max(res,weight[i]);
}
return res;
}
};
class Solution {
public:
int largestComponentSize(vector<int>& nums) {
int n=nums.size();
UnionFind uf(n);
unordered_map<int,int> mp;
int id=0;
for(int i=0;i<n;i++){
if(!mp.count(nums[i])){
mp[nums[i]]=id++;
}
}
for(int i=0;i<n;i++){
for(int j=i+1;j<n;j++){
int id1=mp[nums[i]];
int id2=mp[nums[j]];
if(gcd(nums[i],nums[j])>1){
uf.unite(id1,id2);
}
}
}
return uf.findMaxSet();
}
};
写法二:
weight表示,指向当前节点的节点数(包含孙子节点等)
只要在unite里面加上另一个子树的所有节点 数就行了,find过程中进行的路径压缩,只是调整了指向根节点,但是该根节点的所有节点数是不会变的。
class UnionFind{
private:
vector<int> parent;
vector<int> weight;
public:
UnionFind(int n){
parent.resize(n);
weight.resize(n);
for(int i=0;i<n;i++){
parent[i]=i;
weight[i]=1;//指向当前节点的数量(包含孙子节点等)
}
}
int find(int index){
if(parent[index]==index) return index;
parent[index]=find(parent[index]);
return parent[index];
}
void unite(int index1,int index2){
int p1=find(index1);
int p2=find(index2);
if(p1!=p2){
parent[p1]=p2;
weight[p2]+=weight[p1];//指向根节点的节点数量 加上 子树的节点数量
}
}
int findMaxSet(){
for(int i=0;i<weight.size();i++){
find(i);
}
int res=0;
for(int i=0;i<weight.size();i++){
res=max(res,weight[i]);
}
return res;
}
};
class Solution {
public:
int largestComponentSize(vector<int>& nums) {
int n=nums.size();
UnionFind uf(n);
unordered_map<int,int> mp;
int id=0;
for(int i=0;i<n;i++){
if(!mp.count(nums[i])){
mp[nums[i]]=id++;
}
}
for(int i=0;i<n;i++){
for(int j=i+1;j<n;j++){
int id1=mp[nums[i]];
int id2=mp[nums[j]];
if(gcd(nums[i],nums[j])>1){
uf.unite(id1,id2);
}
}
}
return uf.findMaxSet();
}
};
主要超时原因还是因为两层for循环
方法二:枚举质因数+并查集
基本思路:把关联的加入到并查集中,最后遍历nums,相同的根节点那么数量+1,这样就能找到最多元素的集合了。
由于nums.length最大为
2
?
1
0
4
2*10^4
2?104lianjie
遍历每个值,两两匹配会超时。
因此采用枚举公因式的方式,如果k>=2,且num%k==0,那么k为公约数,对num和k进行联结,以及num和num/k进行联结。不管k或者num/k有没有在nums中这都不要紧,因为后面遍历nums的时候不会遍历到它们。
相比
O
(
4
?
1
0
8
)
O(4*10^8)
O(4?108)的复杂度来的更小。
class UnionFind{
private:
vector<int> parent;
public:
UnionFind(int n){
parent.resize(n);
for(int i=0;i<n;i++){
parent[i]=i;
}
}
int find(int index){
if(parent[index]==index) return index;
return parent[index]=find(parent[index]);
}
void unite(int index1,int index2){
int p1=find(index1);
int p2=find(index2);
if(p1==p2) return;
parent[p1]=p2;
}
};
class Solution {
public:
int largestComponentSize(vector<int>& nums) {
int maxLength=*max_element(nums.begin(),nums.end());
int n=nums.size();
UnionFind uf(maxLength+1);
for(int num:nums){
for(int k=sqrt(num);k>=2;k--){
if(num%k==0){
uf.unite(num,k);//不管k属不属于num都没有关系,把他添加到集合中。因为后续还要遍历一遍nums
uf.unite(num,num/k);
}
}
}
vector<int> cnt(maxLength+1);
int res=0;
for(int num:nums){//遍历nums中的值,同一集合的+1
cnt[uf.find(num)]++;
res=max(res,cnt[uf.find(num)]);
}
return res;
}
};