KMeans算法是一种简单的算法,能够快速,高效的对数据集进行聚类,一般只要通过几次迭代即可。KMeans可以作为一种聚类工具,同时也可以作为一种降维的方式进行特征降维。
KMeans可以通sklearn.cluster.kmeans中进行调用。
from sklearn.datasets import make_blobs
import numpy as np
blob_centers = np.array(
[[ 0.2, 2.3],
[-1.5 , 2.3],
[-2.8, 1.8],
[-2.8, 2.8],
[-2.8, 1.3]])
blob_std = np.array([0.4, 0.3, 0.1, 0.1, 0.1])
X, y = make_blobs(n_samples=2000, centers=blob_centers,
cluster_std=blob_std, random_state=7)
from sklearn.cluster import KMeans
kmeans =KMeans(n_clusters=5)
kmeans.fit(X)
y_pred =kmeans.predict(X)
y_pred
y_pred is kmeans.labels_
kmeans.cluster_centers_##中心位置从中我们可以看出kmeans可以有labels_和cluster_centers_两个函数,kmeans.label_可以显示具体每一个实例的分类副本,而cluster_centers_是显示了分类中心。
现在可以用新的样本进行预测
x_new = np.array([[0,2],[3,2],[-3,3],[-3,2.5]])
kmeans.predict(x_new)
kmeans.transform(x_new)##输出每个实例到5个中间点的距离kmeans.transform()可以显示输入的样本到各个类别中心的距离。
good_init=np.array([[-3,3],[-3,2],[-3,1],[-1,2],[0,2]])
kmeans =KMeans(n_clusters=5,init =good_init,n_init=1)##init为初始中心点,n_init为迭代次数
kmeans.fit(X)
kmeans.inertia_##输出簇内平方和
kmeans.score(X)##返回负惯性kmeans的超参数init是选择中心点的选择方式,n_init为中心点的聚类次数。
kmeans.inertia_是计算样本到簇内中心的距离的平方和,称之为模型的惯性,kmeans.score是输出为负惯性。
kmeans++算法:其算法的目的是使中心点的初始分布更广,算法收敛到次优解的概率减少。可以通过设置参数init为random进行实现。
##实现kmeans++
kmeans_plus = KMeans(n_clusters=5,init='random')
kmeans_plus.fit(X)
kmeans_plus.inertia_加速kmeans:其算法利用三角不等式,简便了计算,提升了运行效率,可以通过algorithm=full进行设置。
##实现加速k-means
kmeans_add =KMeans(n_clusters=5,algorithm='full')
kmeans_add.fit(X)
kmeans.inertia_小批量kmeans:该算法能够在每次迭代的时候使用小批量kmeans稍微移动中心点。使用MiniBatchKMeans。
##小批量kmeans
from sklearn.cluster import MiniBatchKMeans
minibatch_kmeans =MiniBatchKMeans(n_clusters=5)
minibatch_kmeans.fit(X)
minibatch_kmeans.inertia_判断一个分类是否合理可以通过计算数据的轮廓分数,其范围在【-1,1】之间,当其=1是,说明实例分类满足十分靠近所属中心,且远离别的中心。
from sklearn.metrics import silhouette_score
silhouette_score(X,kmeans.labels_)
kmeans_per_k = [KMeans(n_clusters=k, random_state=42).fit(X)
for k in range(1, 10)]
silhouette_scores = [silhouette_score(X, model.labels_)
for model in kmeans_per_k[1:]]
inertias = [model.inertia_ for model in kmeans_per_k]
##对于sihouette_score来说,约接近1说明位置处于自身集群中,且离其他集群很远。
##当接近-1时说明基本上分错集群了
plt.figure(figsize=(8, 3))
plt.plot(range(2, 10), silhouette_scores, "bo-")
plt.xlabel("$k$", fontsize=14)
plt.ylabel("Silhouette score", fontsize=14)
plt.axis([1.8, 8.5, 0.55, 0.7])
plt.show()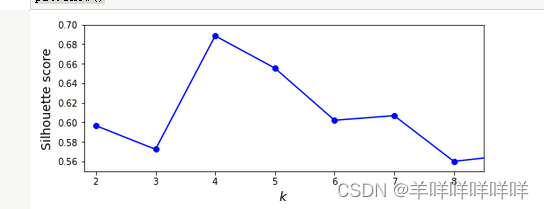
这张图说明了不同k的值的轮廓分数。
实例:使用kmeans进行图像分割
##利用聚类进行图像分割
# Download the ladybug image
import os
import urllib
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "unsupervised_learning"
IMAGES_PATH = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID)
os.makedirs(IMAGES_PATH, exist_ok=True)
images_path = os.path.join(PROJECT_ROOT_DIR, "images", "unsupervised_learning")
os.makedirs(images_path, exist_ok=True)
DOWNLOAD_ROOT = "https://raw.githubusercontent.com/ageron/handson-ml2/master/"
filename = "ladybug.png"
print("Downloading", filename)
url = DOWNLOAD_ROOT + "images/unsupervised_learning/" + filename
urllib.request.urlretrieve(url, os.path.join(images_path, filename))
from matplotlib.image import imread
image = imread(os.path.join(images_path, filename))
kmeans = KMeans(n_clusters=8).fit(X)
segmented_img = kmeans.cluster_centers_[kmeans.labels_]##对实例样本进行调整,变成kmeans聚类的类
segmented_img =segmented_img.reshape(image.shape)
segmented_imgs = []
n_colors = (10, 8, 6, 4, 2)
for n_clusters in n_colors:
kmeans = KMeans(n_clusters=n_clusters, random_state=42).fit(X)
segmented_img = kmeans.cluster_centers_[kmeans.labels_]
segmented_imgs.append(segmented_img.reshape(image.shape))
plt.figure(figsize=(10,5))
plt.subplots_adjust(wspace=0.05, hspace=0.1)
plt.subplot(231)
plt.imshow(image)
plt.title("Original image")
plt.axis('off')
for idx, n_clusters in enumerate(n_colors):
plt.subplot(232 + idx)
plt.imshow(segmented_imgs[idx])
plt.title("{} colors".format(n_clusters))
plt.axis('off')
plt.show()?这里下载了数据,然后通过kmeans进行聚类,然后通过改变聚类的数量,画出图像。

实例2:利用kmeans进行降维与预处理
这里通过MNIST中的图像进行降维处理
from sklearn.datasets import load_digits
X_digits,y_digits =load_digits(return_X_y=True)
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test = train_test_split(X_digits,y_digits)
from sklearn.linear_model import LogisticRegression
log_reg =LogisticRegression()
log_reg.fit(x_train,y_train)
log_reg.score(x_test,y_test)
from sklearn.pipeline import Pipeline
log_kmeans = Pipeline([
('kmeans',KMeans(n_clusters=50)),
('log_reg',LogisticRegression())
])
log_kmeans.fit(x_train,y_train)
from sklearn.model_selection import GridSearchCV
param_grid = dict(kmeans__n_clusters=range(2, 100))
grid_clf = GridSearchCV(log_kmeans,param_grid,cv=3,verbose=2)
grid_clf.fit(x_train,y_train)
grid_clf.best_params_
grid_clf.score(x_test,y_test)
?这里利用逻辑回归进行分类,查看没有使用kmeans时和使用kmeans时的负惯性进行比较,发现效果变好。
实例三:使用kmeans进行半监督学习
##使用聚类进行半监督学习
k =50
kmeans =KMeans(n_clusters=k)
x_digist_dist = kmeans.fit_transform(x_train)
representative_digit_idx =np.argmin(x_digist_dist,axis=0)##找到50个最靠近中心的图片
x_representative_digists=x_train[representative_digit_idx]
x=x_representative_digists
log_reg =LogisticRegression(multi_class="ovr", solver="lbfgs", max_iter=5000, random_state=42)
log_reg.fit(x,y)
log_reg.score(x_test,y_test)
##通过标签传播标记实例
y_train_propagated =np.empty(len(x_train),dtype=np.int32)
print(y_train_propagated)
for i in range(k):
y_train_propagated[kmeans.labels_==i]=y[i]
log_reg =LogisticRegression(multi_class="ovr", solver="lbfgs", max_iter=5000, random_state=42)
log_reg.fit(x_train,y_train_propagated)
log_reg.score(x_test,y_test)?上面是通过给50个样本进行人工标注,进行训练后,将标记的标签传播到所有的样本传播到同意集群的所有实例中,这里包括了集群边界的实例,但会导致错误标记。
percentile_cloest=20
x_cluster_dist =x_digist_dist[np.arange(len(x_train)),kmeans.labels_]
x_cluster_dist
for i in range(k):
in_cluster =(kmeans.labels_==i)
cluster_dist = x_cluster_dist[in_cluster]
cutoff_distance=np.percentile(cluster_dist,percentile_cloest)
above_cutoff = (x_cluster_dist>cutoff_distance)
x_cluster_dist[in_cluster&above_cutoff]=-1
partially_propagated =(x_cluster_dist !=-1)
x_train_partially=x_train[partially_propagated]
y_train_partially =y_train[partially_propagated]
log_reg =LogisticRegression(multi_class="ovr", solver="lbfgs", max_iter=5000, random_state=42)
log_reg.fit(x_train_partially,y_train_partially)
log_reg.score(x_test,y_test)以上是筛选了靠近中心的20%的数据进行标记,然后进行训练。
DBSCAN聚类算法:它是定义了高密度的连续区域,它是通过收到参数eps画一个圆,统计圆内的样本数,最小样本数由min_samples来决定,而且DBSCAN只能用于分类,但不能预测。
##DBSCAN
from sklearn.cluster import DBSCAN
from sklearn.datasets import make_moons
X,y=make_moons(n_samples=1000,noise=0.05)
dbscan =DBSCAN(eps=0.05,min_samples=5)##min_samples说明一个核心实例中至少要包含5个实例,eps=0.05说明区域是以0.05为半径
dbscan.fit(X)
dbscan.labels_
##当数值=-1时,说明算法将数据视为异常
dbscan.core_sample_indices_##核心实例的索引
dbscan.components_##核心实例本身dbscan.labels_显示实例分类的副本,dbscan.core_sample_indices显示数据的核心实例索引。
dbscan.components_显示核心实例的坐标。
实例四:对Olivetti的人脸数据进行聚类,并判断是否拥有正确的集群数。
from sklearn.datasets import fetch_olivetti_faces
data =fetch_olivetti_faces()对数据集进行分层分类
from sklearn.model_selection import StratifiedShuffleSplit
sss = StratifiedShuffleSplit(n_splits=1,test_size=40,random_state=42)
train_index,test_index = next(sss.split(data.data,data.target))
x_train=data.data[train_index]
y_train =data.target[train_index]
x_test=data.data[test_index]
y_test=data.target[test_index]
sss_val = StratifiedShuffleSplit(n_splits=1,test_size=80,random_state=42)
train_index,val_index =next(sss_val.split(x_train,y_train))
x_train_new =x_train[train_index]
y_train_new =y_train[train_index]
x_val =x_train[val_index]
y_val =y_train[val_index]选择效果最好的聚类个数
from sklearn.cluster import KMeans
kmeans =[KMeans(n_clusters=n).fit(x_train) for n in range(1,200,5)]
from sklearn.metrics import silhouette_score
silhouette_score =[silhouette_score(x_train,kmeans[i].labels_) for i in range(2,40)]
silhouette_score
plt.figure(figsize=(20, 20))
plt.plot(range(6,196,5), silhouette_score, "bo-")
plt.xlabel("$k$", fontsize=14)
plt.ylabel("Silhouette score", fontsize=14)
plt.show()
kmeans =KMeans(n_clusters=135)
kmeans.fit(x_train)
kmeans.inertia_显示结果