环形链表有一个非常重要的特点,那就是一旦开始遍历,就无法停止,一直循环,会超出时间限制
常见的几种形式(圆圈内为存储的数据值)
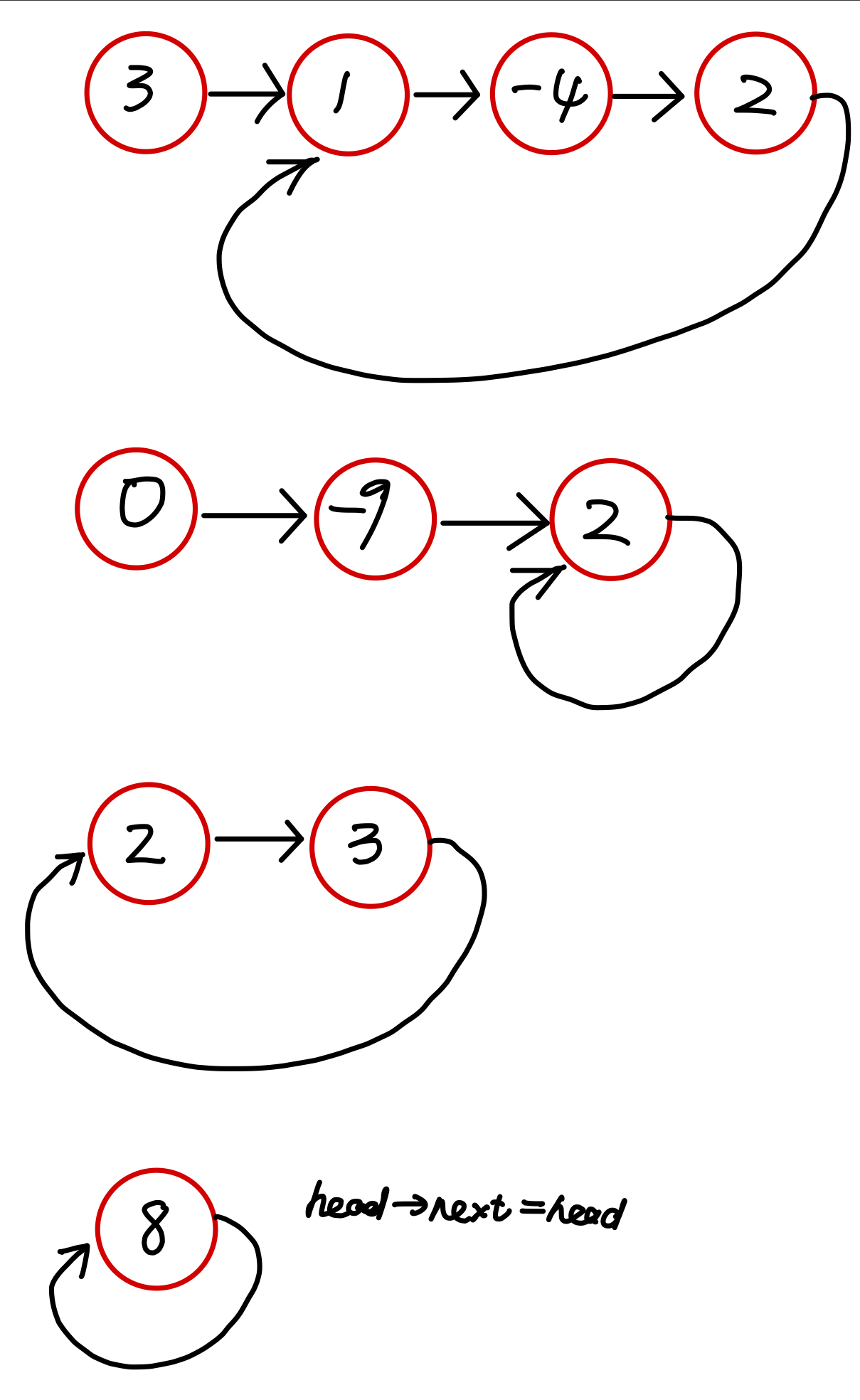
解决这个题的一个比较常规的思路
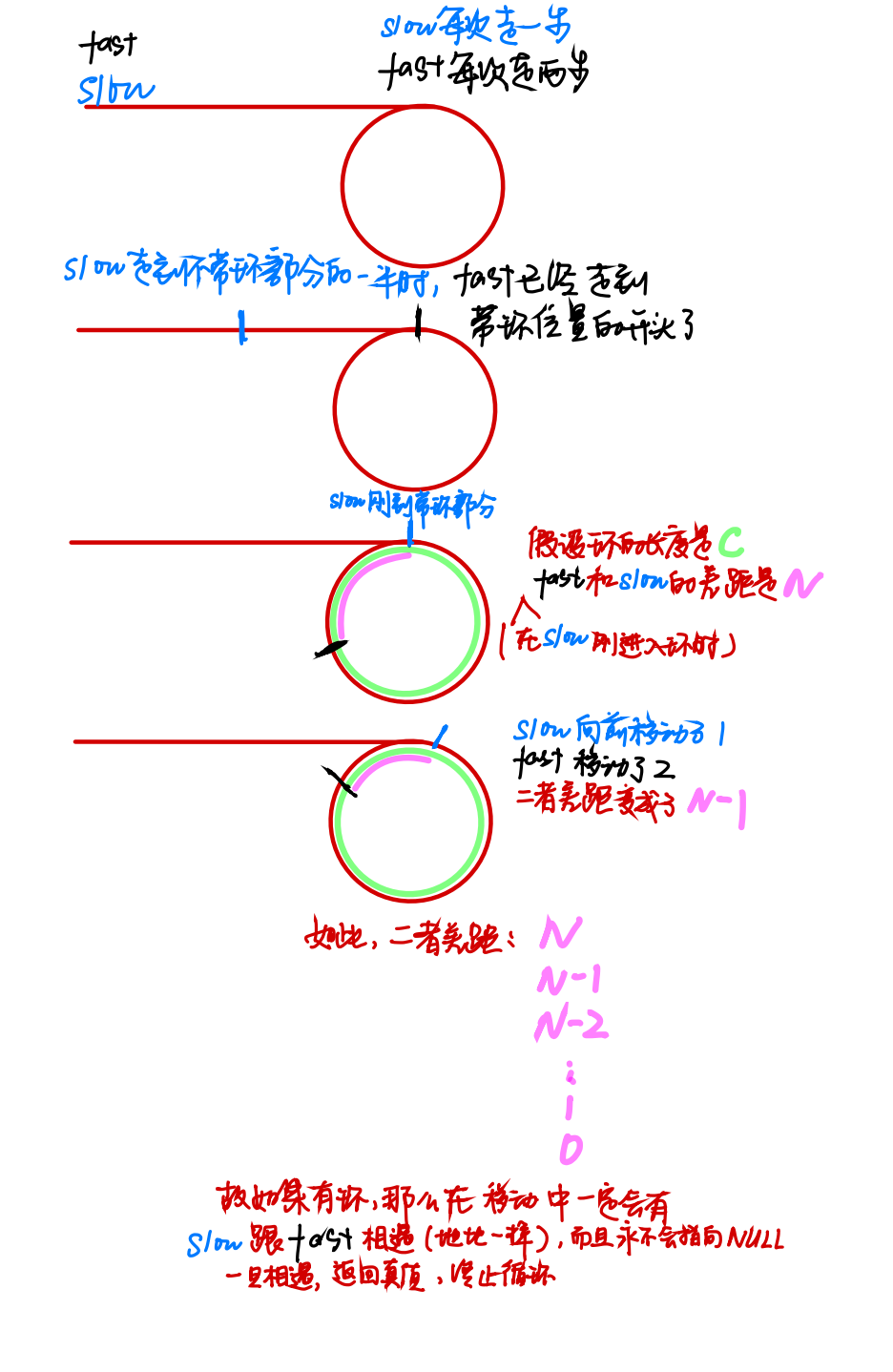
设置一快一慢两个指针,快的指针每次走2步,慢的每次走1步
在慢的指针走到环的时候,快的指针早就到了环里了,因此可以看作快的指针跑到了慢的后面(类似于套圈吧
而且快的指针与慢的指针有差距,由于快的指针每次2步,慢的1步,因此差距在以每次为1的速度削减,直到最后减到0
此时指针相交
既然快的指针和慢的指针能相交,就说明了有环,否则快的指针一定先指向NULL,且两者一定不会相遇

这个题的重点不在于这个题本身,而在于它衍生出来的疑问
- slow一次走1步,fast一次走3步,fast能追上slow吗?fast一次走4步呢?走n步呢?请证明
- 请求出链表环的入口点
- slow一次走1步,fast一次走3步,fast能追上slow吗?fast一次走4步呢?走n步呢?请证明
不一定能追上,特殊情况下可能永远追不上!
先看fast一次走3步的情况
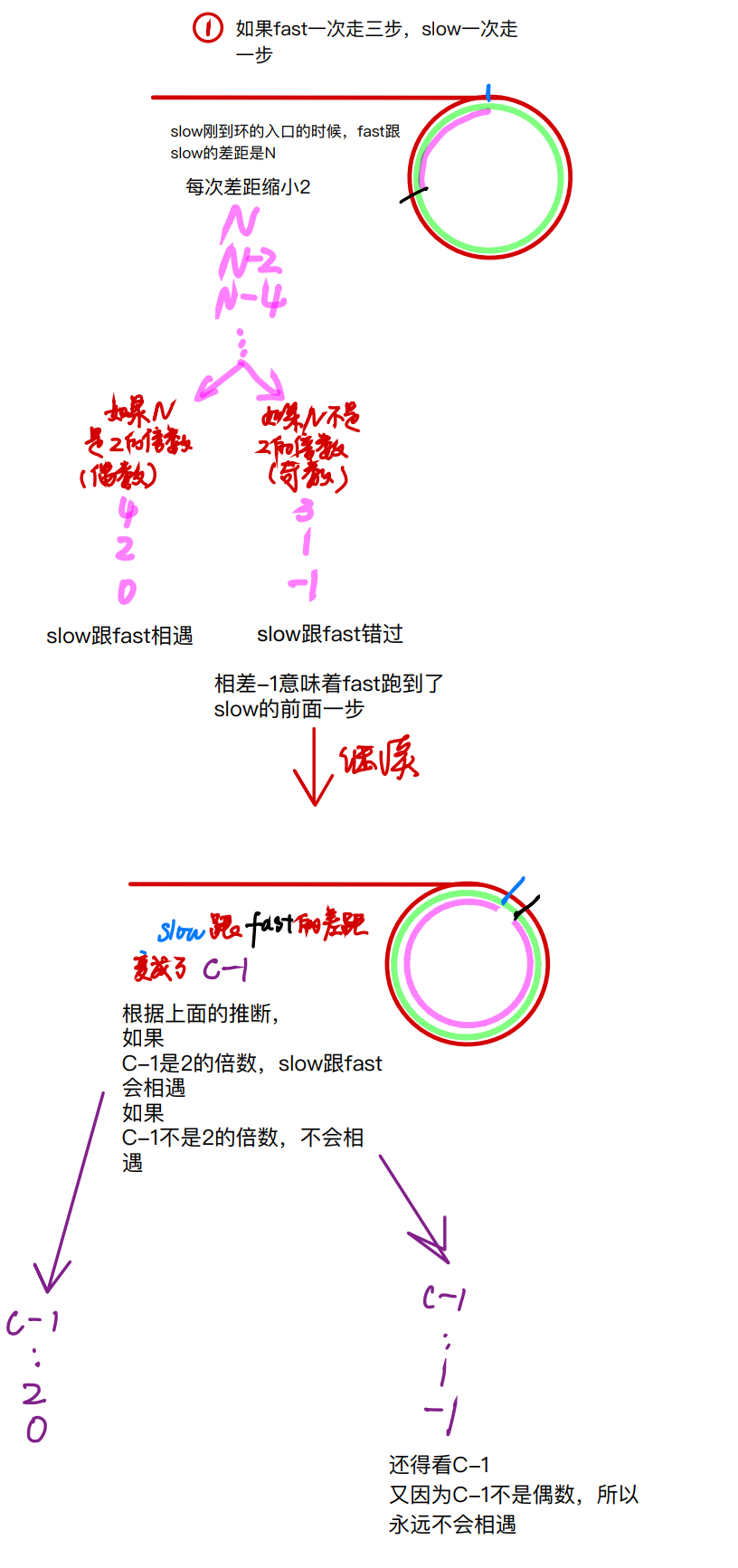
再看一次走4步和n步的情况

因此fast走2步,slow走1步,两者步幅差为1,N和C一定是整数,一定能追上
其余情况要看N和C的大小
在没给出环的具体长度时, N和C都是不确定的
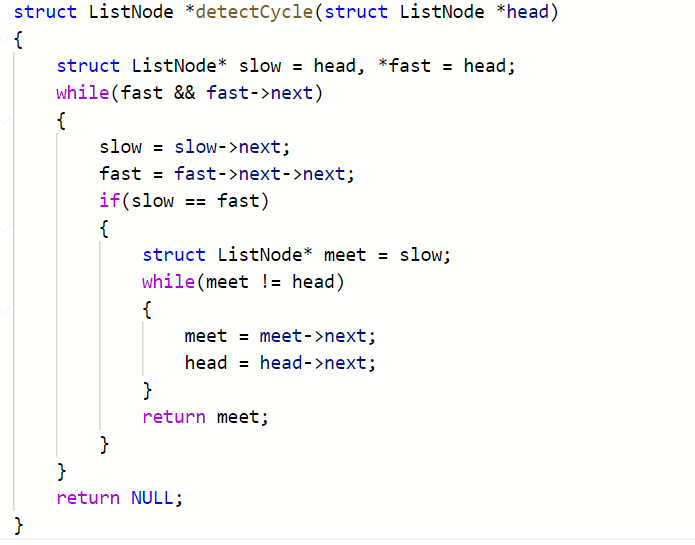
- 请求出链表环的入口点
假设slow跟fast在meet结点相遇
【meet】 到 【环入口点】 的距离设为 X
【链表头】 到 【环入口点】的距离设为 L
【环】的长 度设为 C
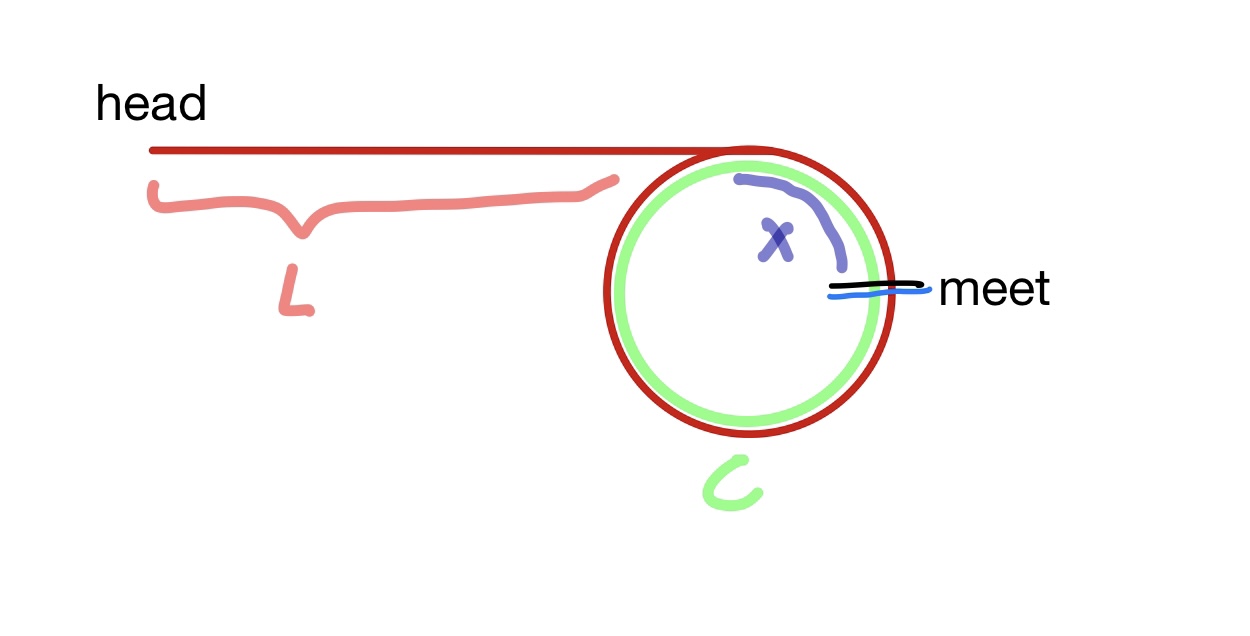
根据上面的分析,slow一次走一步,fast一次走两步,那么
fast走过的路程的slow的2倍
slow跟fast相遇时,slow一定是处于刚进入环的第一圈
因为二者一定会在距离差为负数(也就是fast跑到slow前面)之前相遇,而fast的速度又比slow快
但是fast不知道已经跑了几圈了,假设fast跑了n圈
那么slow的路程为 L+X
fast的路程为 L+X+n*C
得到等式
2*(L+X)=L+X+n *C
L+X=n*C
L=n*C-X
L的长度跟n*C-X的长度一样
也就是说从meet走上n圈再往回退X步,距离跟L一样
而从meet走上n圈再往回退X步,就是环入口点的位置
L也是从head到环入口点的距离
所以得到的结论就是
如果从head和从meet同时出发,一次走一步,一定会相遇在环入口点
(这个结论就无关了fast绕圈次数n还有环的长度C、不带环部分的长度L了,因为测试用例不同这些值就不同,但根据公式会得到客观结论)
结束
That’s all, thanks for reading!💐