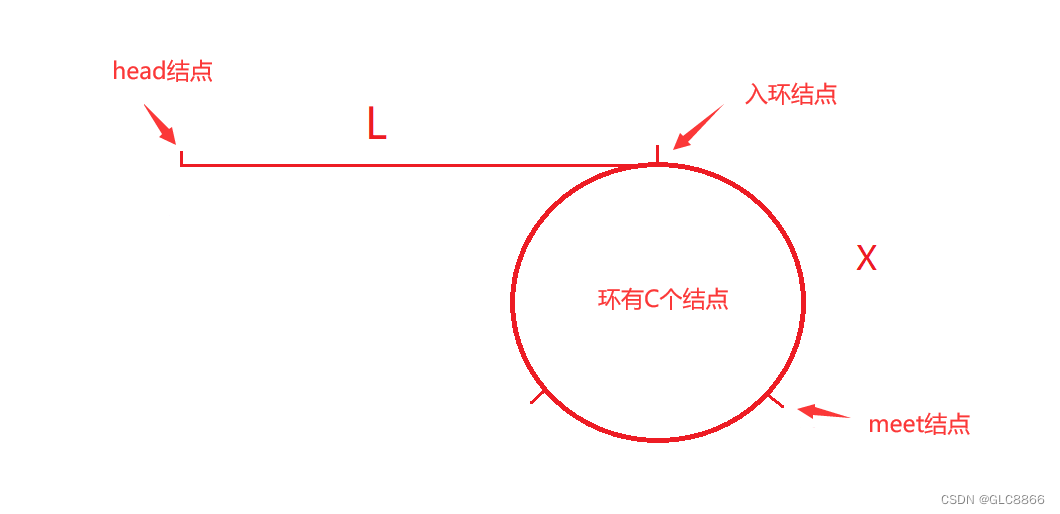
思路:利用快慢指针,构建等式,寻找规律。
1、创建指针slow和fast从head同时出发,slow一步走1个结点,fast一步走2个结点。
因为fast比slow快,当slow到达入环结点时,他们在环内之间的距离是每走一步就会缩短1结点,所以一定会相遇重合。
2、设head结点到入环结点需要走L个结点。
3、设环共有C个结点。
当slow入环时,fast可能在环的任意位置,此时fast如果在入环结点的前一个位置时,是slow与fast要在环内相遇,走的距离最远的情况,此时fast要追上slow需要走C-1步,slow自然也就走C-1个结点,slow一定是在环内走完一圈之前与fast相遇的。
4、设slow入环后,再走X个结点就会在meet结点处与fast相遇重合。
5、当slow从head到达入环结点时,fast已经在环内走了L个结点,fast有可能一圈都没有走完,也有可能走了好几圈,这取决于圈的大小。我们可以确定的是:fast与slow相遇时,一定在环内走了超过一圈以上的。
6、设fast与slow相遇时,已经在环内完整地走了N圈(N>=1),再算上超过整圈的部分X和未入环时的L,那么fast从head开始到与slow相遇时,总走了L+N*C+X个结点。
7、因为fast的速度时slow的两倍,所以fast走的节点数也可以用2L+2X表示。
8、构建等式:L+N*C+X==2L+2X,得到L==N*C-X。
9、创建两个指针cur1=head和cur2=meet。上一条的结论公式中,L理解为cur1走L个结点,N*C-X理解为cur2走N*C个结点再"退"X个结点,他们将会在入环结点处相遇重合。
//判断链表是否为环,如果是环,则返回快慢指针重合的结点。如果不是环,则返回NULL。
struct ListNode* JudgeLoop(struct ListNode *head)
{
struct ListNode* slow=head;
struct ListNode* fast=head;
while(fast&&fast->next)
{
fast=fast->next->next;
slow=slow->next;
if(fast==slow)
return fast;
}
return NULL;
}
struct ListNode *detectCycle(struct ListNode *head)
{
struct ListNode* meet=JudgeLoop(head);
//meet不为NULL,说明有环。
if(meet)
{
struct ListNode* cur1=head;
struct ListNode* cur2=meet;
while(cur1!=cur2)//每一步都走一个结点,推理可知一定会入环结点处相遇。
{
cur1=cur1->next;
cur2=cur2->next;
}
return cur1;
}
else
{
return NULL;
}
}