目录
一、栈
1、栈的基本介绍
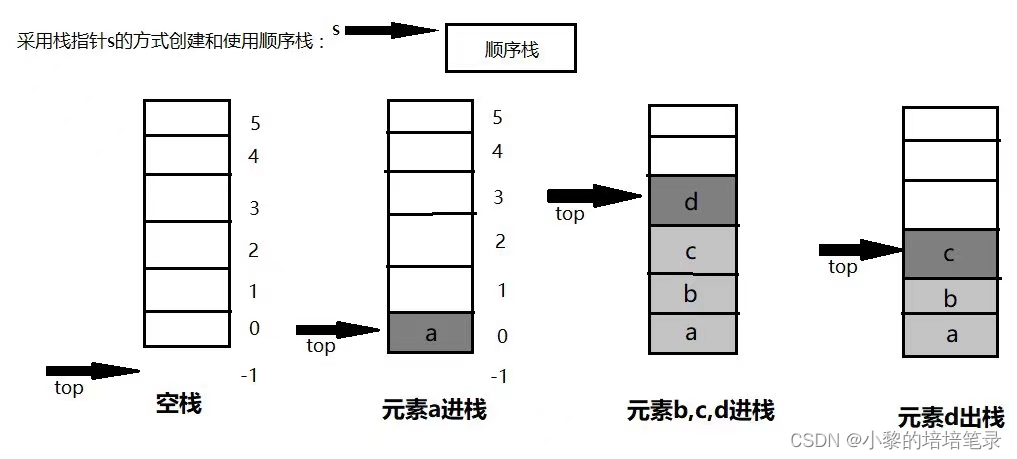
????????栈是?个先?后出的有序列表。栈(stack)是限制线性表中元素的插?和删除只能在线性表的同?端进?的?种特殊线性表。允许插?和删除的?端,为变化的?端,称为栈顶(Top),另?端为固定的?端,称为栈底(Bottom)。
????????根据栈的定义可知,最先放?栈中元素在栈底,最后放?的元素在栈顶,?删除元素刚好相反,最后放?的元素最先删除,最先放?的元素最后删除。
?2、栈的底层实现
? (1)创建一个类,模拟栈
? ? ? ? maxSize :栈的最大容量
? ? ? ? top :表示栈顶
? ? ? ? stack :数组用来存储数据
public class Stacks { public int maxSize; public int top ; public int[] stack; //构造器,传入栈的最大容量 public Stacks(int maxSize) { this.maxSize = maxSize; //初始化栈顶的位置为-1,栈空 top = -1; //初始化数组,最大容量为栈的容量 stack = new int[maxSize]; } }? (2)判断栈空和栈满
? ? ??????? 栈满
//因为底层是数组存储数据,所以索引从0开始, //判断条件为 top == maxSize - 1 public boolean isFull(){ return top == maxSize - 1; }? ? ? 栈空
public boolean isEmpty(){ return top == -1; }? (3)入栈操作
? ? ? ? 首先判断是否栈满,栈满后则不能继续添加,先对栈顶进行加一,然后再放入数据。
public void push(int data){ //判断是否栈满 if (isFull()){ System.out.println("栈满,无法入栈"); return; } top++; stack[top] = data; }? (4)出栈操作
? ? ? ? 首先判断栈空,出栈操作其实就是将top减一即可,return stack[top--]; 这样操作是为了让我们知道出栈的数据是什么。
public int pop(){ if (isEmpty()){ throw new RuntimeException("栈空,无法出栈!"); } //先出栈,后减减 return stack[top--]; }? (5)显示栈数据
public void show(){ if (isEmpty()){ System.out.println("栈空,无法显示!"); return; } for (int i = top ; i >= 0; i--){ System.out.printf("stack[%d] = %d\n", i , stack[i]); } }
二、中缀表达式转后缀表达式
?1、拆解中缀表达式
? ? ? ? 首先将中缀表达式拆解成一个一个的字符,存放到集合中,方便后面我们将中缀转后缀时的遍历操作。
首先用split分割操作将原数据分割到数组中存放,然后用增强for循环遍历并同时存放到创建好的stringList集合中。
public static List<String> endList(String s){ String[] s1 = s.split(""); List<String> stringList = new ArrayList<>(); for (String s2 : s1) { stringList.add(s2); } return stringList; }?? 补充运算符优先级的判断
? ? ? ? 后面我们转换成后缀表达式时,需要判断运算符的优先级。
public static int Calcu(String s){ char ch = s.charAt(0); if (ch == '-' || ch == '+'){ return 0; } else if (ch == '*' || ch == '/') { return 1; } return -1; }2、中缀转后缀的算法
? ? 初始化两个栈:运算符栈s1和储存中间结果的栈s2
? ? 从左至右扫描中缀表达式
? ? 遇到操作数时,将其压s2
? ? 遇到运算符时, 比较其与s1栈顶运算符的优先级
???????如果s1为空,或栈顶运算符为左括号“(”,则直接将此运算符入栈
???????否则,若优先级比栈项运算符的高,也将运算符压入s1
???????否则,将s1栈顶的运算符弹出并压入到s2中 ,再次与s1中新的栈顶运算符相比较
? ? 遇到括号时:
??????? 如果是左括号“(”,则直接压入s1
? ? ? ? 如果是右括号“)”,则依次弹出s1栈顶的运算符, 并压入s2,直到遇到左括号为止,此时将这一对括号丢弃
? ? 重复步骤2至5,直到表达式的最右边
? ? 将s1中剩余的运算符依次弹出并压入s2
? ? 依次弹出s2中的元素并输出,结果的逆序即为中缀表达式对应的后缀表达式3、中缀转后缀代码解析
? ? ? ? 前面的算法说到,首先创建两个栈一个运算符栈和一个中间结果栈,但是根据上面算法的介绍,中间结果栈没有出栈操作,就是数据全部是存入,于是在写代码的时候我们可以将中间结果栈换成集合来存放数据。
?
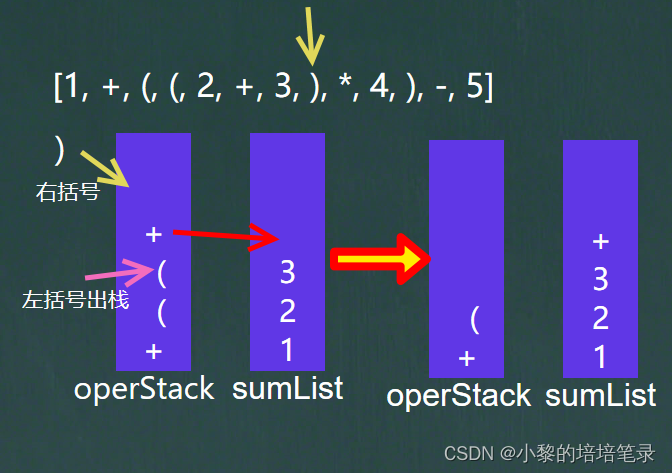
? ? ? ? ?首先用增强for循环遍历原数据集合,然后进行判断,如果是数字就放入右方的集合中,如果是运算符就放入左方的符号栈中。
? ? ? ?进行运算符判断,如果是左括号“(? ” 就直接放入符号栈中,如果是右括号“ )”,就取出符号栈栈顶的符号放入集合中,直到遇到左括号“(? ”,停止将栈顶的符号放入集合中,此时将栈顶出栈也就是去掉括号。
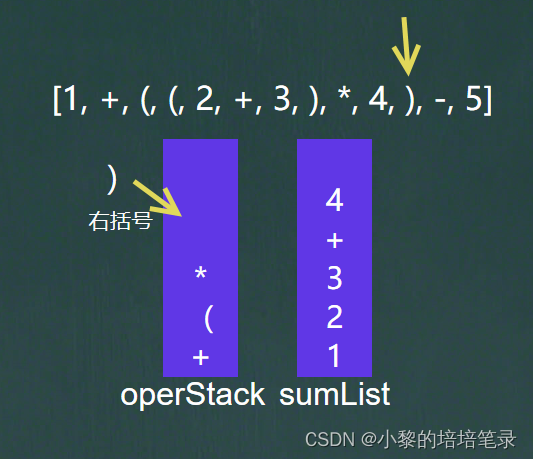
?????????然后继续进行遍历放入数据和符号,如果是符号,就与符号栈的栈顶的符号进行比较,要放入运算符的运算级如果小于等于栈顶运算符的运算级,就将栈顶的运算符放入集合中,但下面的图中,运算符为括号,所以不用管,因为括号有单独的判断条件,所以直接放入。
? ? ? ? 遇到右括号又继续重复前面的操作。
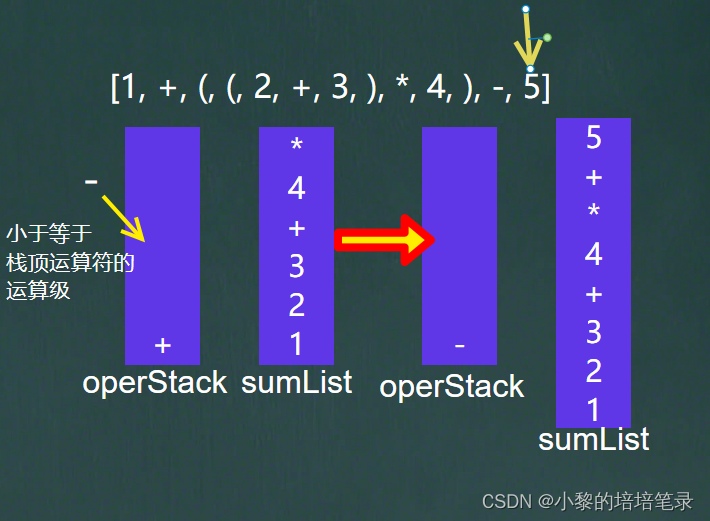
? ? ? ? 放入运算符的优先级小于等于栈顶运算符的优先级,于是将栈顶的运算符放入集合中,然后放入的运算符继续放入符号栈中。
? ? ? ? ?最后循环结束,将符号栈中的运算符依次放入到集合中。
public static List<String> MiddleToEndExpress(List<String> strings){ //创建栈,存放运算符 Stack<String> operStack = new Stack<>(); //因为这个栈不需要出栈,所以使用集合 List<String> sumList = new ArrayList<>(); for (String s : strings) { //判断是否是数据 if (s.matches("\\d+")){ sumList.add(s);//是数据直接加入 }else if (s.equals("(")){//判断是否是左括号 operStack.push(s);//是,直接放入符号栈 }else if (s.equals(")")){//判断是否是右括号 while (!operStack.peek().equals("(")){//如果栈顶是左括号,退出循环 sumList.add(operStack.pop());//不是左括号,就将栈顶的符号依次放入集合 } //循环结束,表示栈顶是左括号,把左括号去掉,就去掉了一对括号 operStack.pop(); }else {//前面的判断都不是,那就是运算符 //如果符号栈为空,并且运算符小于等于栈顶的运算符优先级 while (operStack.size() != 0 && Calcu(s) <= Calcu(operStack.peek())){ //就将栈顶的运算符放入集合中 sumList.add(operStack.pop()); } //然后将符号放入符号栈中 operStack.push(s); } } //遍历结束,将符号栈剩余的符号依次取出放入集合中 while (operStack.size() != 0){ sumList.add(operStack.pop()); } //最后将集合返回 return sumList; }最后结果为:结果中不能含括号,否则转换错误!
4、对后缀表达式进行计算
? ? ? ? 前面我们已经将中缀转成后缀表达式了,那么我们只需要直接计算了,首先还是遍历我们的集合(存放后缀表达式的)将数据暂时放入栈中方便我们操作,然后在遍历过程中进行判断,如果是数据就直接放入栈中,如果是运算符就从栈中取出两个数据进行运算,运算结果又放入栈中,直到栈中只存在一个数据时,就是最后的运算结果。
public static int endCalculator(List<String> stringList){ //创建栈,存放数据 Stack<String> dataStack = new Stack<>(); //循环遍历集合 for (String s : stringList) { //正则表达式判断是否是数据,如果是,就放入栈中 if (s.matches("\\d+")){ dataStack.push(s); }else {//否则就是运算符 //取出两个数据 int num1 = Integer.parseInt(dataStack.pop()); int num2 = Integer.parseInt(dataStack.pop()); //存放运算结果的变量 int res = 0; //判断运算符继续相应的运算 if (s.equals("+")){ res = num1 + num2; }else if (s.equals("-")) { res = num2 - num1; }else if (s.equals("*")) { res = num1 * num2; }else if (s.equals("/")) { res = num2 / num1; }else { throw new RuntimeException("运算符异常!"); } //运算过后将结果又放入栈中 dataStack.push("" + res); } } //最后返回栈中唯一的数据既是结果 return Integer.parseInt(dataStack.pop()); }