题目内容
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
示例 1:
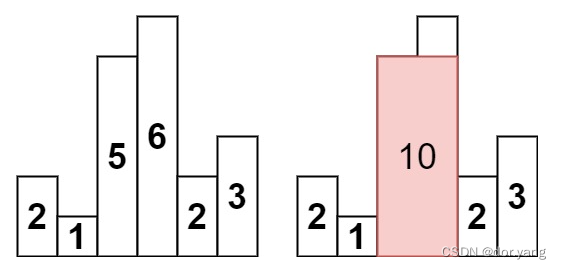
输入:heights = [2,1,5,6,2,3]
输出:10
解释:最大的矩形为图中红色区域,面积为 10
示例 2:
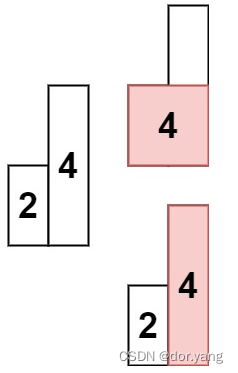
输入: heights = [2,4]
输出: 4
提示:
1 <= heights.length <=105
0 <= heights[i] <= 104
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/largest-rectangle-in-histogram
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解题思路
这个题目说来好笑,我的第一个想法是动态规划,就是以这个节点作为最后一个节点的时候,我们能得到的最大的矩阵有多大,我设置了一个数组来存储大小,还用了一个数组来存放这个最大矩阵是从哪里开始的,然后我们根据这个最大的矩阵的高度,和我们下一个节点的高度对比,来决定我们后续的操作。
如果这个点小于,那么我们首先想到的就是这个矩阵一起变矮,然后变粗,这个就是情况1,然后我还想到,因为变矮了,所以左边也可能可以扩展,所以我们向左遍历,这个就是情况2,然后两者取最大的就是结果。
如果这个点大于,那么首先情况1就是这个点迁就一下,我们一样用之前的高度,得到一个加粗的矩阵,这个是情况1,另外,我们还可以向左遍历,找到所有比这个高度高的节点,另算这个情况中的最大矩阵。同样是两者比较,取最大作为结果。
这个思路我完善了好几次,最后已经没有问题了,却喜提TLE(毕竟这个确实是也不算动态规划)。不过,我觉得其实还是有机会的,所以我注释掉之后也附在这里了。
然后,我就开始思考新的方法。于是,我想到了单调栈。
我可以通过单调栈,找到最左和最右的,比我的当前节点要小的高度,然后在此之间的,都已我这个节点为准,计算矩阵大小。不过需要注意的就是,为了防止最左最右因为不存在导致栈里数据没有都出来,我在输入的数组的左右都加了一个0,确保能够得到完整的左右数据。最后遍历,计算最大矩阵大小即可。
当然,这个思路就是只能说是可以完成,性能上确实是不能算好,比如说我们可以不遍历,在单调栈里直接处理矩阵完成比较,不过这些我当时就已经不是很想搞了,被折磨的有点久。。
实现代码
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
// vector<int> big;big.push_back(heights[0]);
// vector<int> from;from.push_back(0);
// int ans=big[0];
// for(int i=1;i<heights.size();i++){
// int gao=big[i-1]/(i-from[i-1]);
// if(heights[i]<gao){
// int xuan1=heights[i]*(i-from[i-1]+1);
// int xuan2=0;
// int j;int xiao=heights[i];
// for(j=i-1;j>=0;j--){
// if(heights[j]<xiao){
// break;
// }
// }
// j++;
// xuan2=(i-j+1)*xiao;
// int input=xuan1>xuan2?xuan1:xuan2;
// big.push_back(input);
// ans=ans>input?ans:input;
// from.push_back(xuan1>xuan2?from[i-1]:j);
// }
// else{
// int j;int xiao=heights[i];int check=heights[i];int where=i;
// for(j=i-1;;j--){
// if(heights[j]<=gao){
// break;
// }
// xiao=xiao<heights[j]?xiao:heights[j];
// if(check<xiao*(i-j+1)){
// where=j;
// }
// check=check<xiao*(i-j+1)?xiao*(i-j+1):check;
// }
// j++;
// // check=check<xiao*(i-j+1)?xiao*(i-j+1):check;
// // cout<<i<<" "<<j<<" "<<check<<" "<<endl;
// if(check<gao*(i-from[i-1]+1)){
// big.push_back(gao*(i-from[i-1]+1));
// ans=ans>gao*(i-from[i-1]+1)?ans:gao*(i-from[i-1]+1);
// from.push_back(from[i-1]);
// }
// else{
// big.push_back(check);
// ans=ans>check?ans:check;
// from.push_back(where);
// }
// }
// }
// // for(int i=0;i<heights.size();i++){
// // cout<<from[i]<<" ";
// // }
// // cout<<endl;
// return ans;
stack<int> zhan;
heights.push_back(0);
heights.insert(heights.begin(),0);
map<int,vector<int>> mp;
for(int i=0;i<heights.size();i++){
if(zhan.empty()){
zhan.push(i);
}
else{
while(heights[zhan.top()]>heights[i]){
int l=zhan.top();
zhan.pop();
vector<int> mid;
mid.push_back(zhan.empty()?0:zhan.top());
mid.push_back(i);
mp.insert(pair<int,vector<int>>(l,mid));
if(zhan.empty()){
break;
}
}
zhan.push(i);
}
}
int ans=0;
for(map<int,vector<int>>::iterator it=mp.begin();it!=mp.end();it++){
// cout<<it->first<<" "<<it->second[0]<<" "<<it->second[1]<<endl;
ans=ans>heights[it->first]*(it->second[1]-it->second[0]-1)?ans:heights[it->first]*(it->second[1]-it->second[0]-1);
}
return ans;
}
};
// [15,18,18,3,7,11,2,13,18,15,18,6,6,1,17,15,2,15,0,0]
// [1,9,3,7,3,2,1,3,6,5,9,1,2,7,6,5,9,4]
// [5,5,1,7,1,1,5,2,7,6]
// [0,1,0,2,1,0,1,3,2,1,2,1]
// [1,2,3,4,5]
// [2,4]
后来的优化
之前我已经是用单调栈很粗糙的完成了问题,后来就开始思考优化的方案,其实还是很简单的,就是我一开始单调栈的结果使用map<int,vector>来存储的,所以我第一次优化去掉了map,在单调栈的计算过程中,去计算的矩阵大小并完成比较。之后我又去掉了vector,之所以分两次纯粹是嫌麻烦。。最后结果还是不错的。
优化代码
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
stack<int> zhan;
heights.push_back(0);
heights.insert(heights.begin(),0);
map<int,vector<int>> mp;
for(int i=0;i<heights.size();i++){
if(zhan.empty()){
zhan.push(i);
}
else{
while(heights[zhan.top()]>heights[i]){
int l=zhan.top();
zhan.pop();
vector<int> mid;
mid.push_back(zhan.empty()?0:zhan.top());
mid.push_back(i);
mp.insert(pair<int,vector<int>>(l,mid));
if(zhan.empty()){
break;
}
}
zhan.push(i);
}
}
int ans=0;
for(map<int,vector<int>>::iterator it=mp.begin();it!=mp.end();it++){
// cout<<it->first<<" "<<it->second[0]<<" "<<it->second[1]<<endl;
ans=ans>heights[it->first]*(it->second[1]-it->second[0]-1)?ans:heights[it->first]*(it->second[1]-it->second[0]-1);
}
return ans;
}
};
// [15,18,18,3,7,11,2,13,18,15,18,6,6,1,17,15,2,15,0,0]
// [1,9,3,7,3,2,1,3,6,5,9,1,2,7,6,5,9,4]
// [5,5,1,7,1,1,5,2,7,6]
// [0,1,0,2,1,0,1,3,2,1,2,1]
// [1,2,3,4,5]
// [2,4]