8.1 排序的基本概念
排序定义

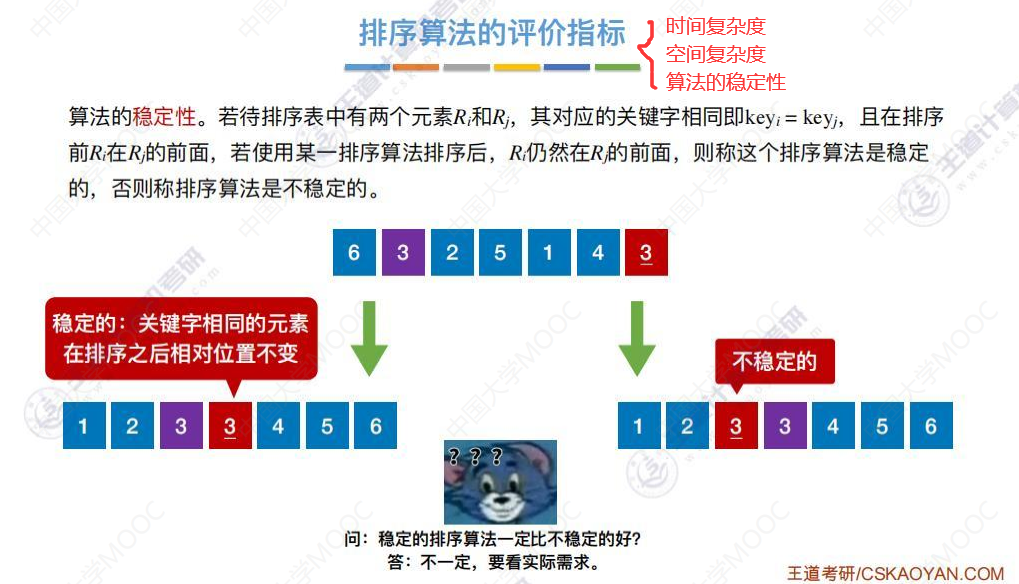
排序算法的评价指标
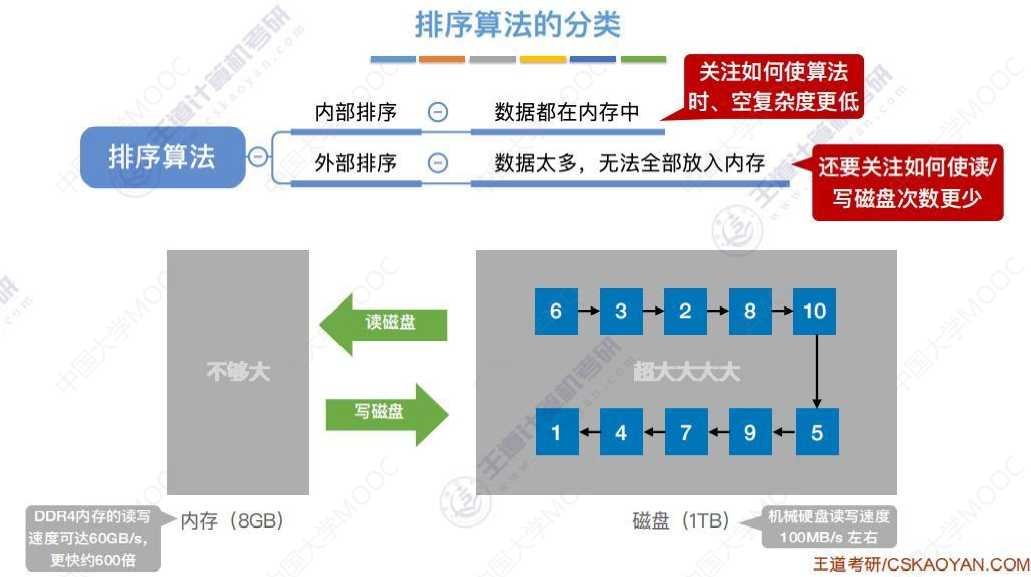
排序算法的分类
总结

https:/www.cs.usfca.edu/~galles/visualization/Algorithms.html
8.2-1 插入排序
插入排序举例
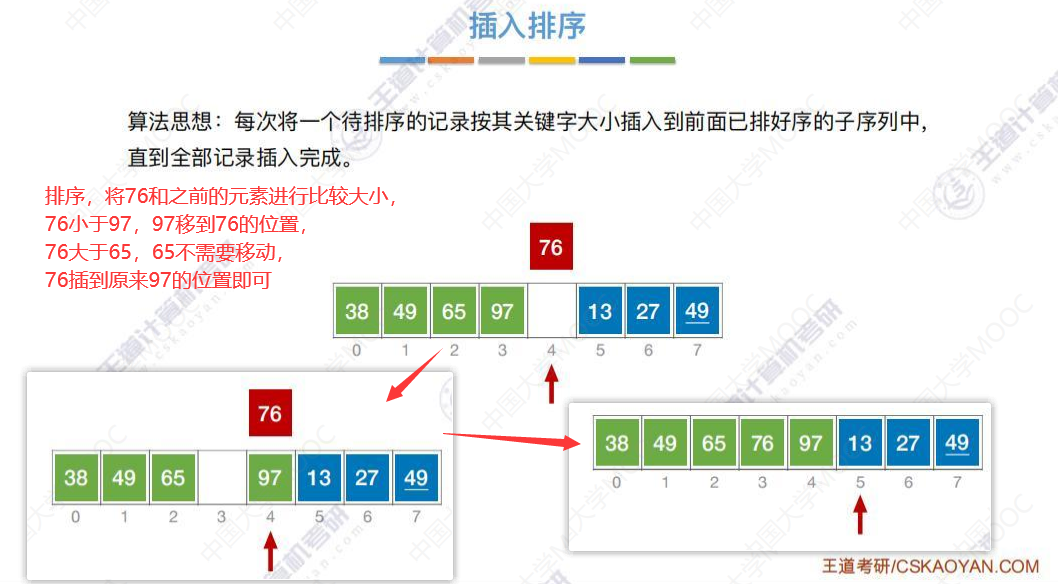
插入排序算法实现
插入排序一般实现



插入排序带哨兵实现

算法效率分析
空间复杂度

时间复杂度


下图:比如第一趟:查找70,对照着对待,A[2]=70<A[1]=80,对比关键字一次,A[0]=A[i]=70,移动元素一次,for循环,A[0]=70<A[1]=80,又对比关键字一次,A[2]=A[1]=80,又移动元素一次,最A[1]=A[0]=70,又移动元素一次。共对比关键字2次,移动元素3次

平均时间复杂度O(n2)

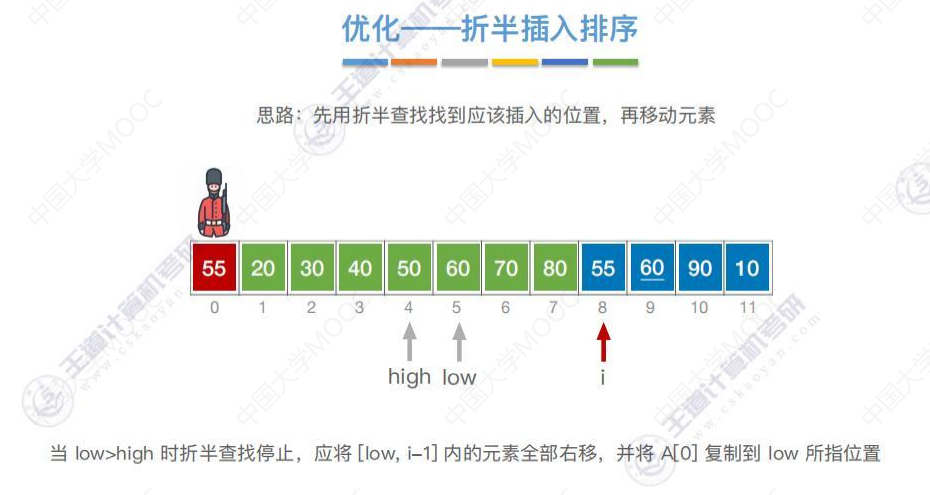
优化—折半插入排序
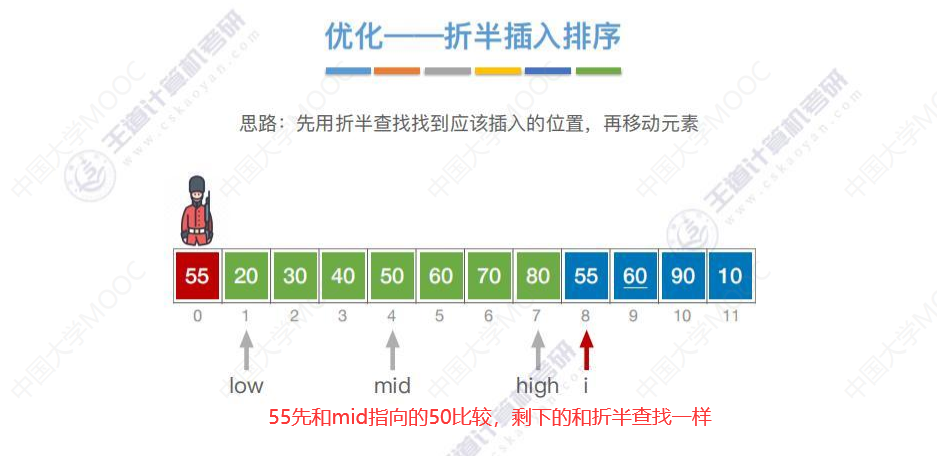

8.2-2 希尔排序
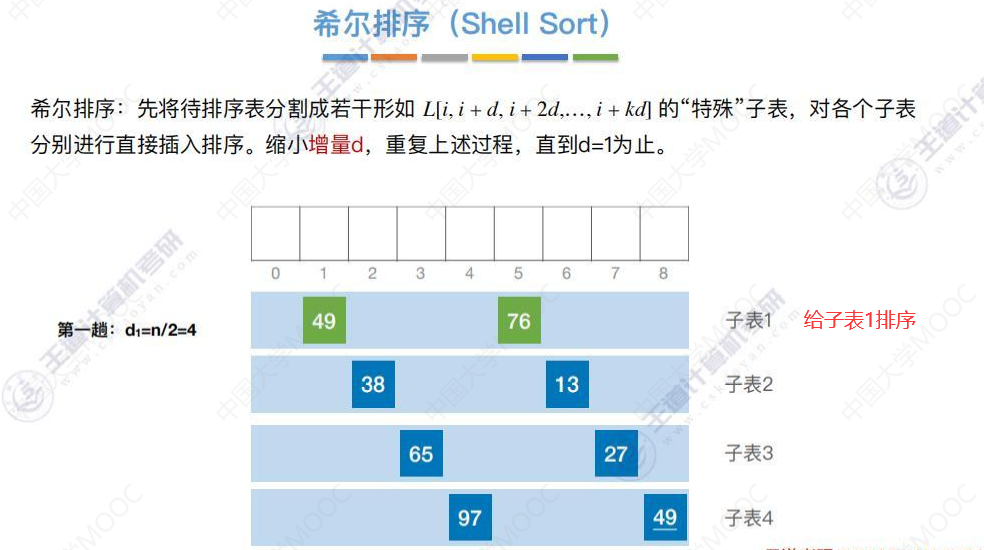
希尔排序示例
第一趟:


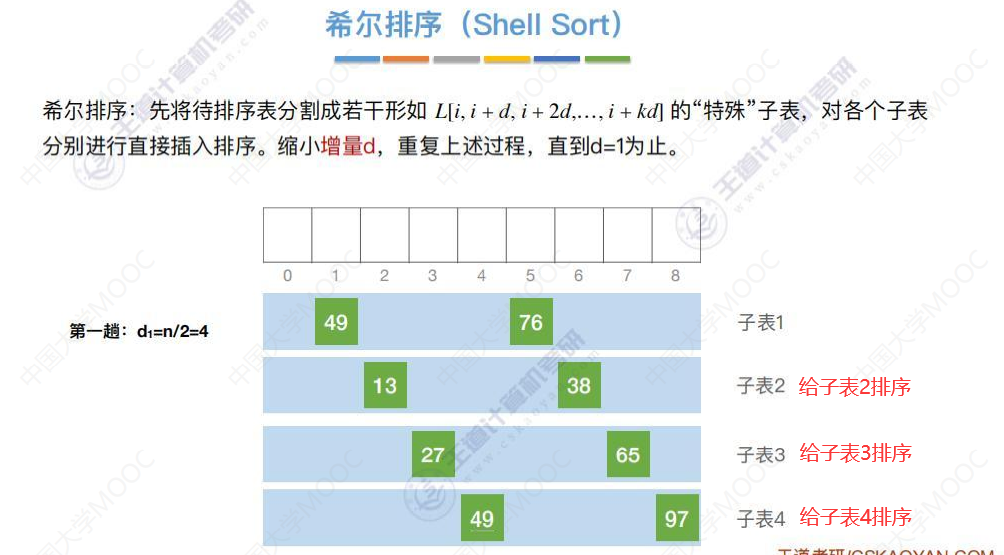
第二趟:



第三趟:


希尔建议设置每次将来增量缩小一半
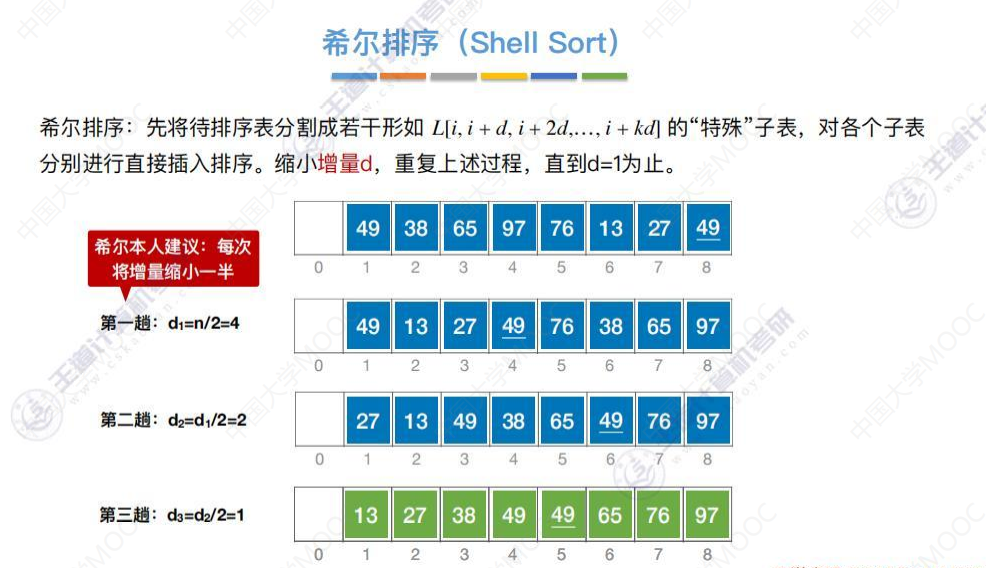
算法实现
下图只是实现希尔排序的一种方法,但是这种方法并不是按照上面的思路:先分成多个子表,每个子表排完序再放回数组,更换d的大小,继续这样的操作。但下图的方法仍然能实现希尔排序。由于时间原因暂时没能实现上述思路的希尔排序的代码。
下图方法的思路是:逐步的遍历每个子表,在逐步遍历过程中使得每个子表都更有序一点,循环往复。


第一趟分别比较76和49,13和39,27和65,49和97.
第一趟结束时,第二趟开始时如下:

第二趟:d=4/2=2,从27开始比较,++i,顺次比较49和之前的13,比较76跟之前的27,38和之前的49,65和之前的76,97和之前38。

第二趟结束时,第三趟开始时如下:

第三趟结束时如下

算法性能分析
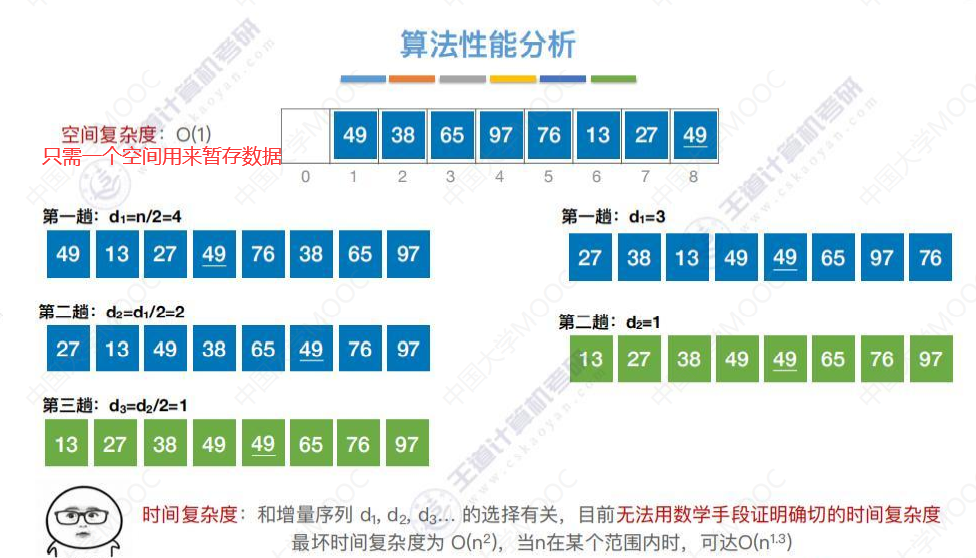

因为需要用增量d来快速的找到与之相邻的从属于同一个子表的元素,所以只有具有随机访问的特性才能完成这个事情。所以必须用顺序表。
8.3-1冒泡排序
算法实现
升序排列,从后往前冒泡,将小的值冒泡到前面。
当然也可以从前往后冒泡。
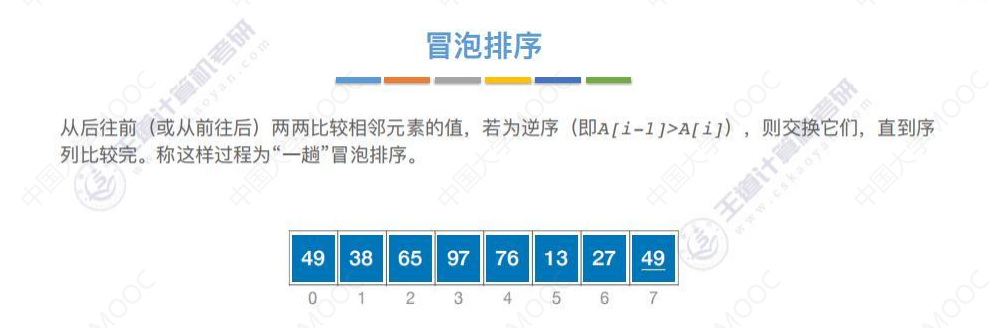
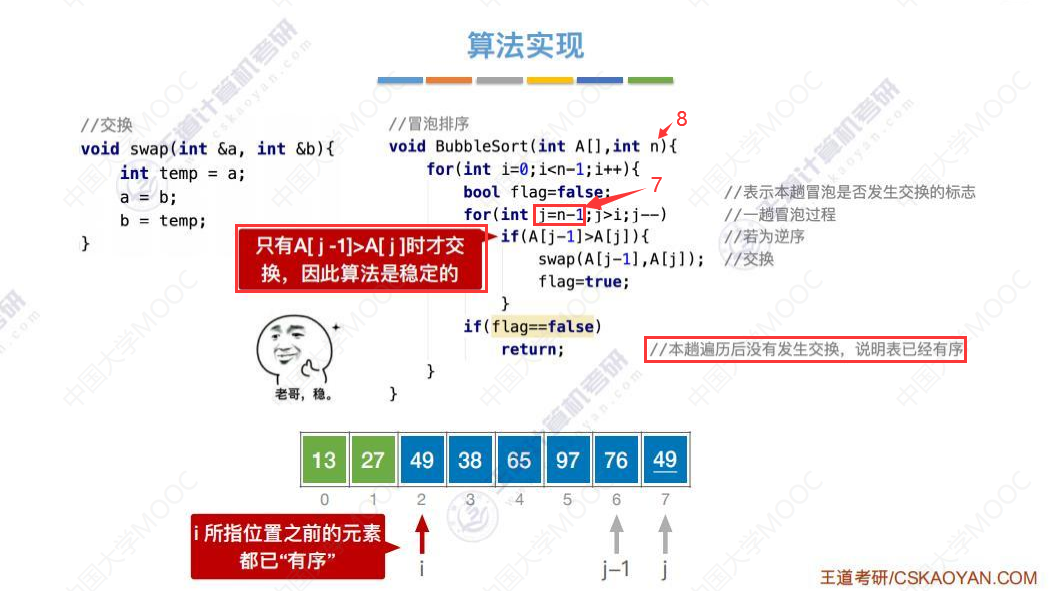
算法性能分析
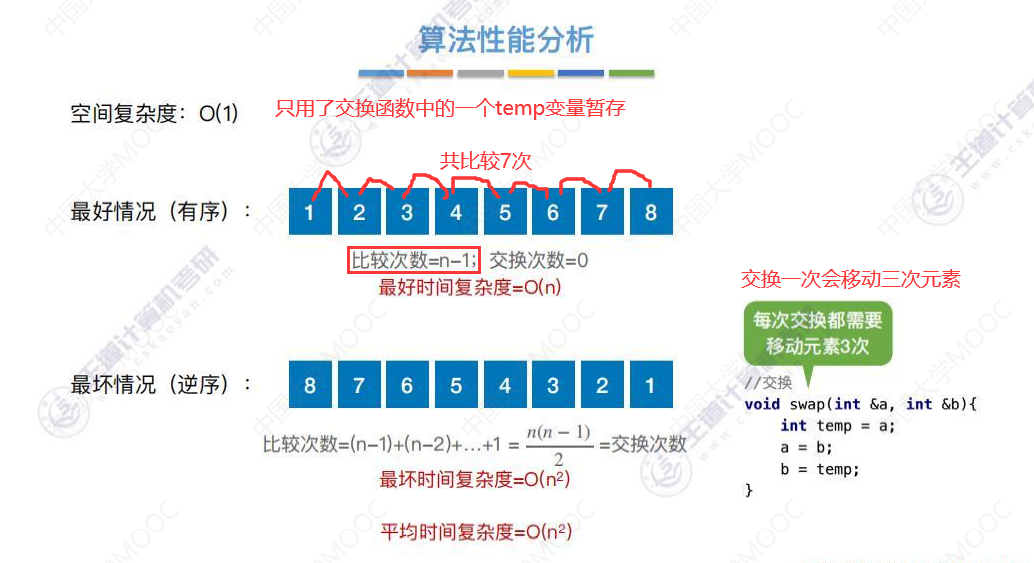
冒泡排序适用于链表
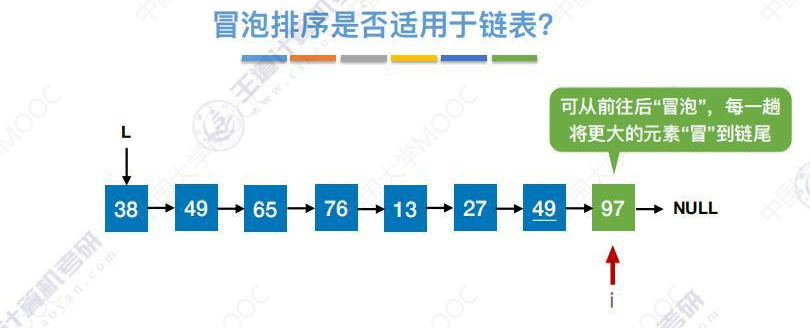
8.3-2 快速排序
快速排序算法思想

快速排序代码

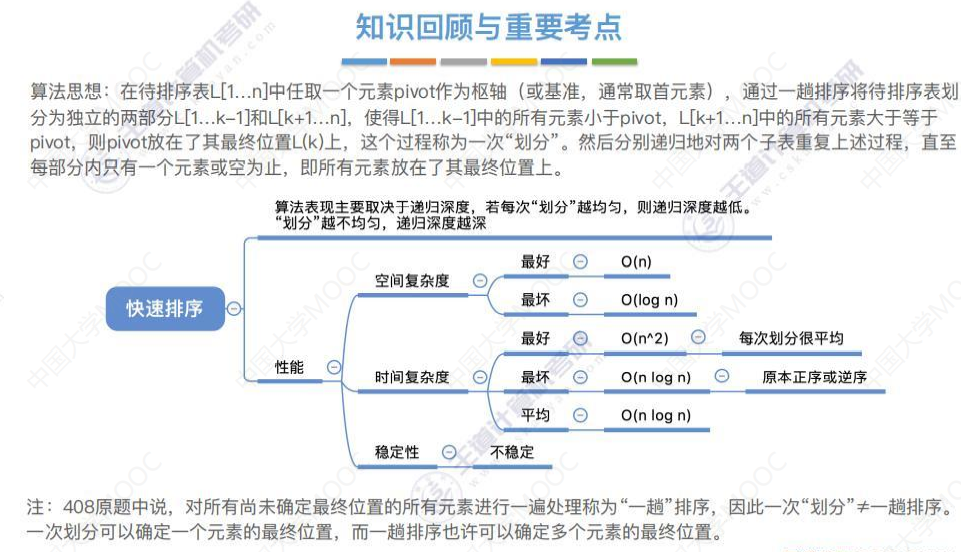
算法效率分析
时间复杂度

下面的分析是不严谨的,因为比较一次元素可能带来元素的移动,也可能不带来元素的移动,这里我们按照比较一次元素就按O(1)计算。那么比如下图这个初始序列,要比较每一个元素,所有我按O(n)处理。
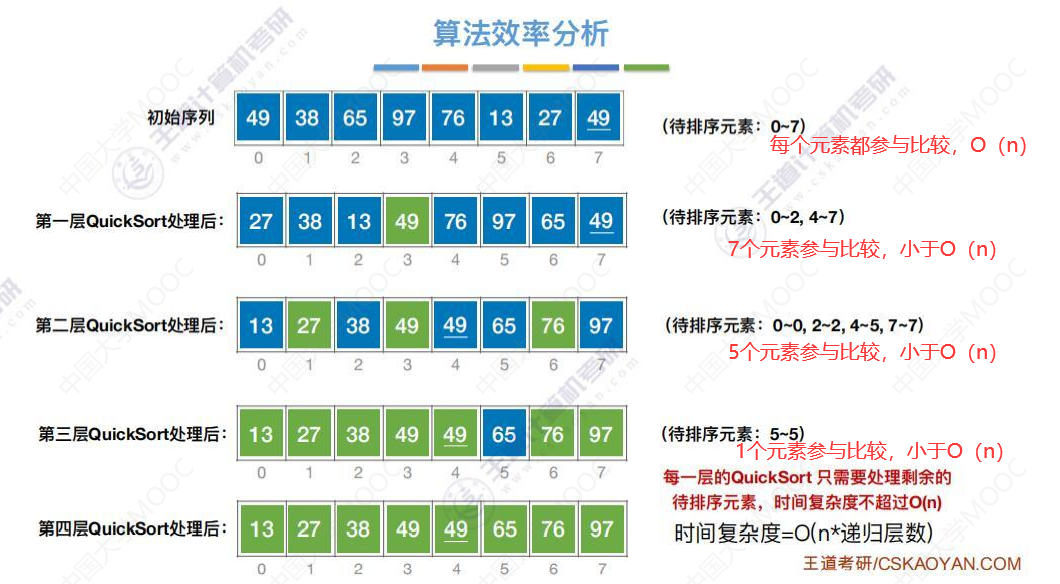
空间复杂度
QuickSort()函数在执行时,不断地递归会占用多层递归工作栈,所以这里空间复杂度和递归层数有关。空间复杂度=O(递归层数)
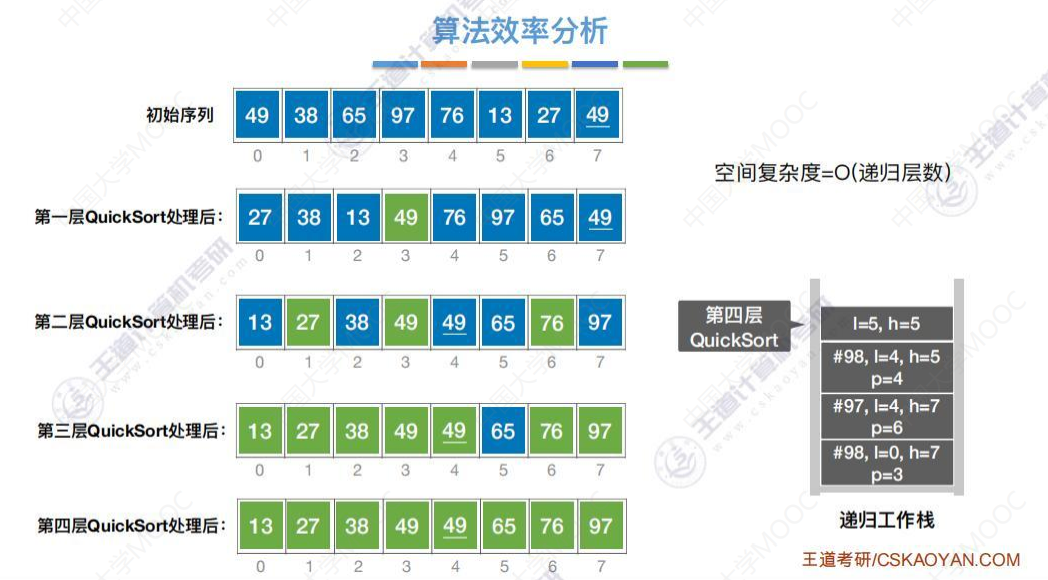
把快速排序过程梳理成二叉树

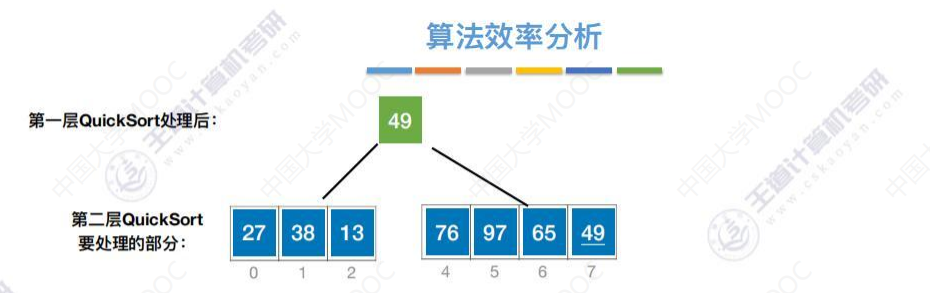
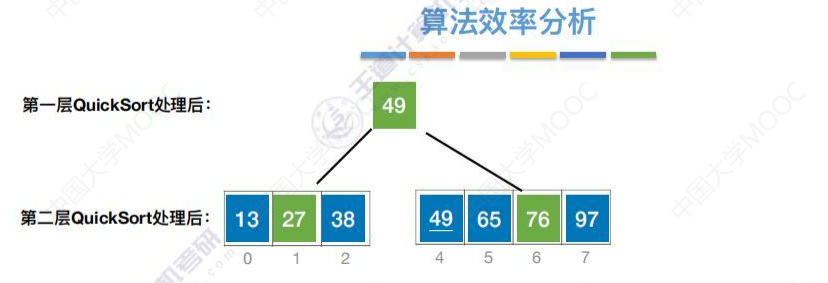
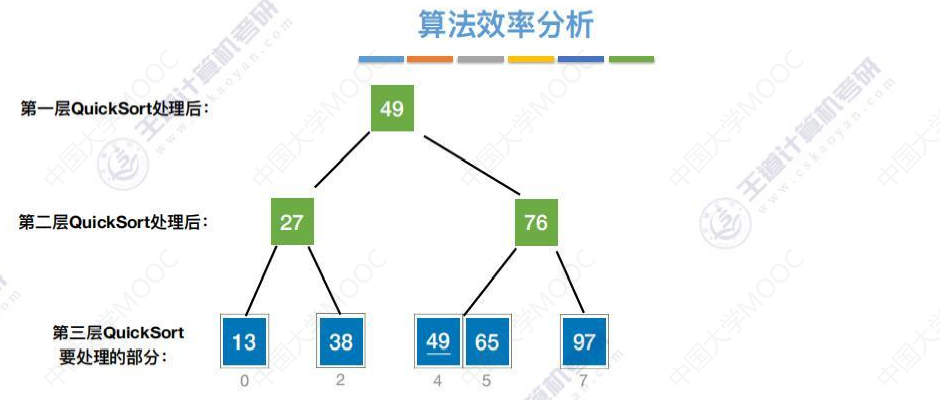
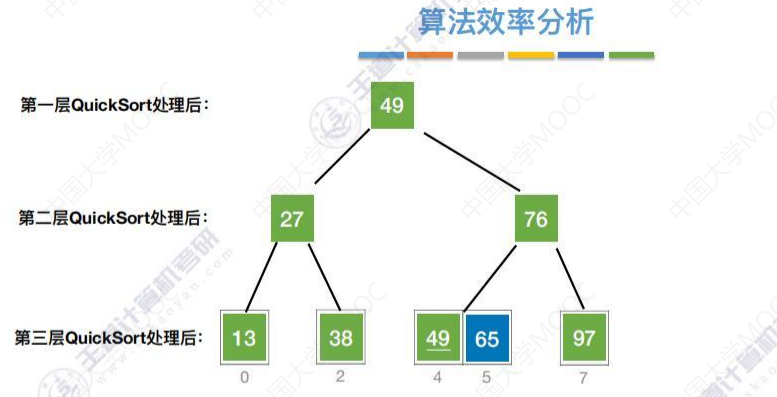
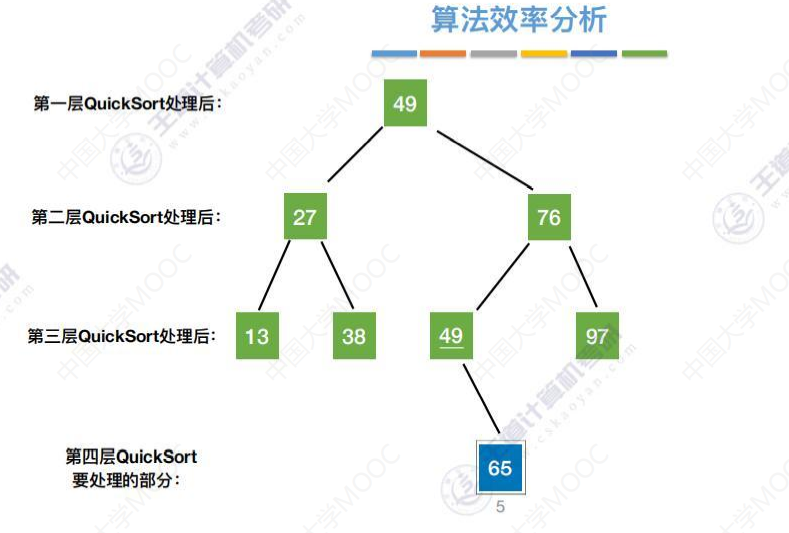
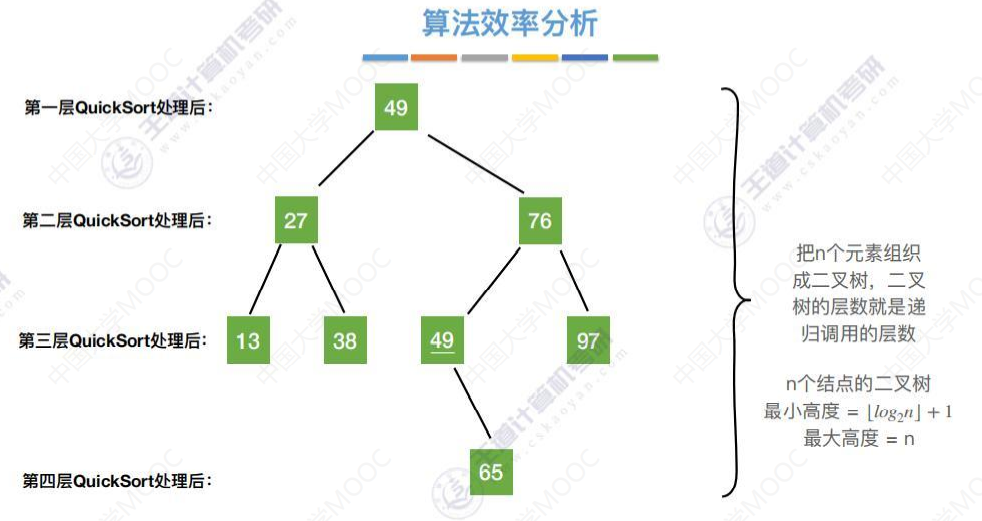

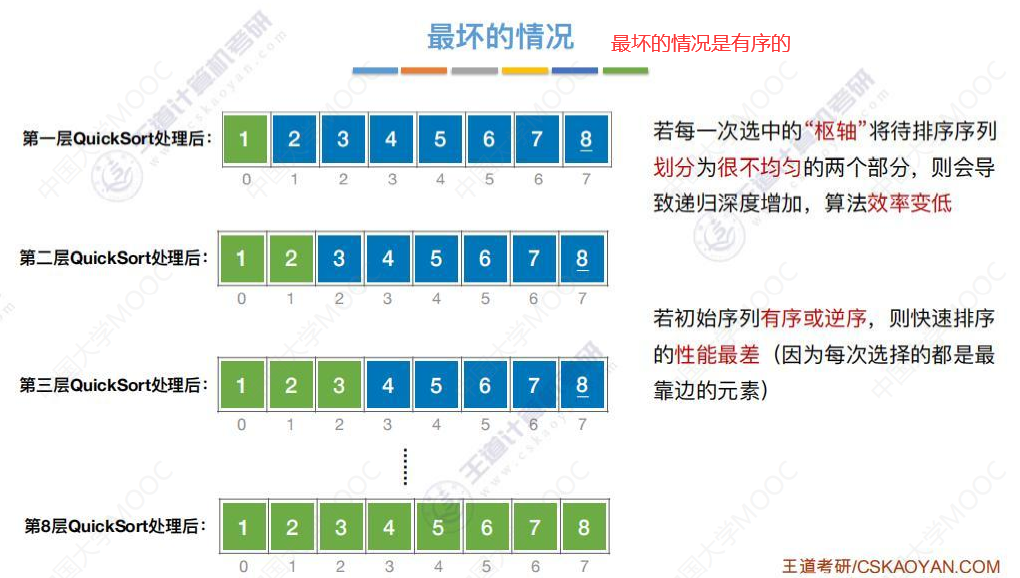
最坏的情况
若给的序列是有序的,那么每次划分都很不均匀
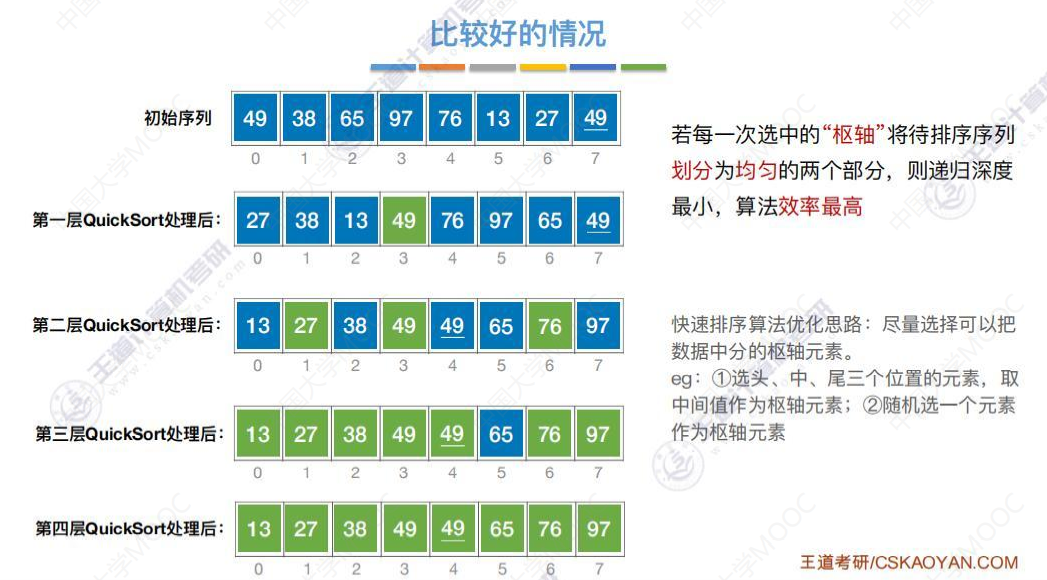
比较好的情况
优化思路②随机选一个元素作为枢轴元素:因为是随机的,所以不太可能每次都选到最大的或者最小的,所以划分比较均匀。
实际应用中
在实际应用当中,快速排序算法的平均时间复杂度其实要接近于最好的时间复杂度,而不是接近最坏,所以在实际应用当中,快排这个算法是所有内部排序算法当中平均性能最优的排序算法。

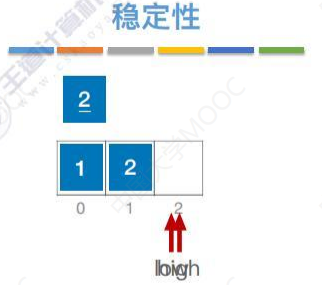
稳定性
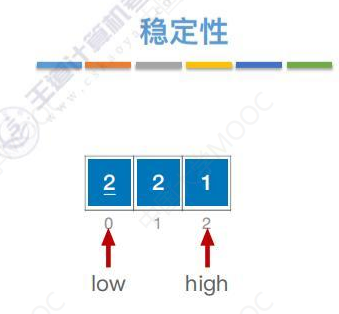
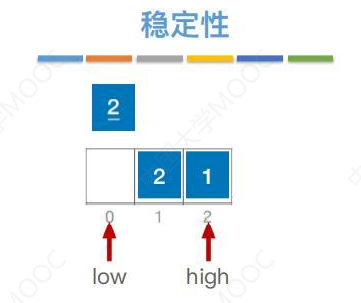
1比2小,转移到数组编号0的位置。
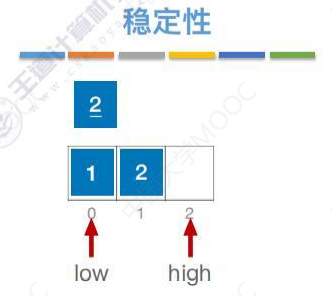
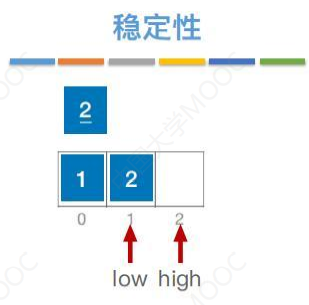
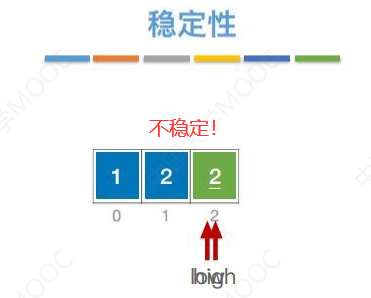
总结
8.4-1简单选择排序

下图有两个49,当49是最小的时,我们优先将最前面的49移动到头部的位置使之有序。
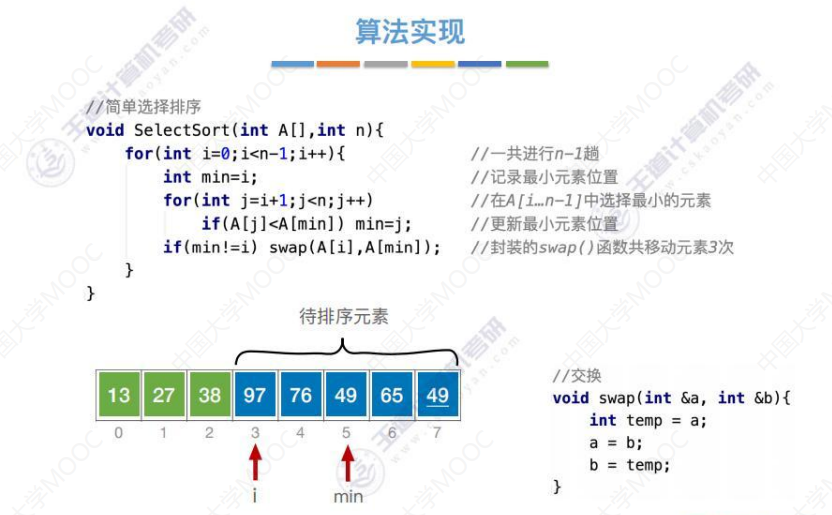
算法性能分析
n个元素的简单选择排序需要n-1趟处理。
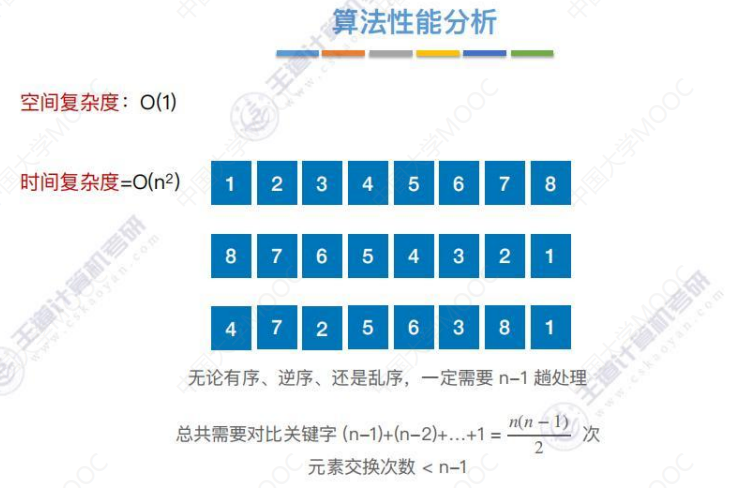
稳定性分析

8.4-2 堆排序
什么是堆?

回忆二叉树的顺序存储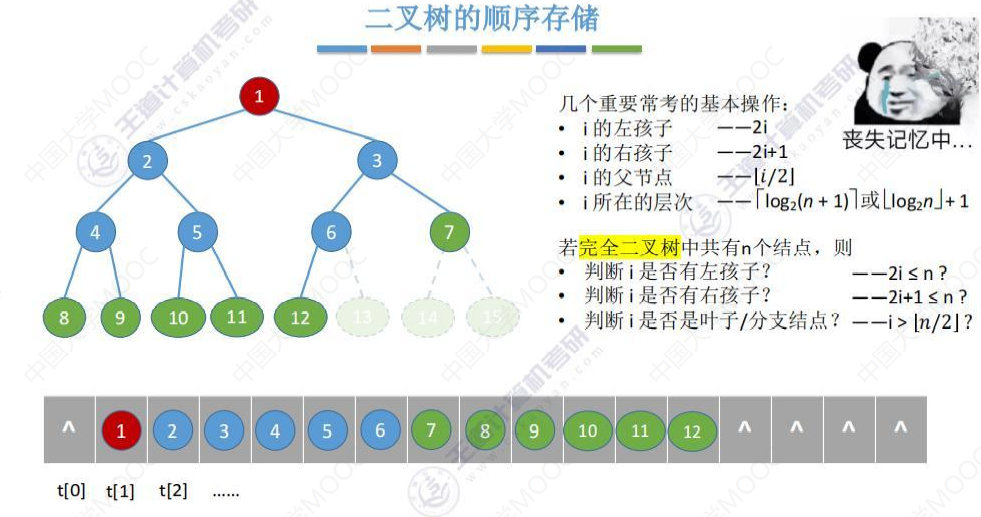
大根堆
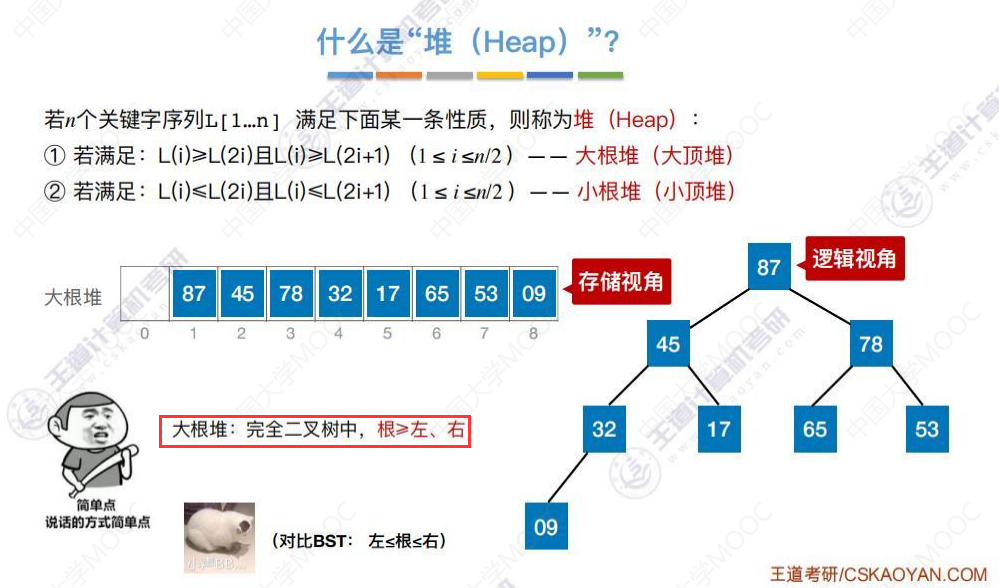
小根堆
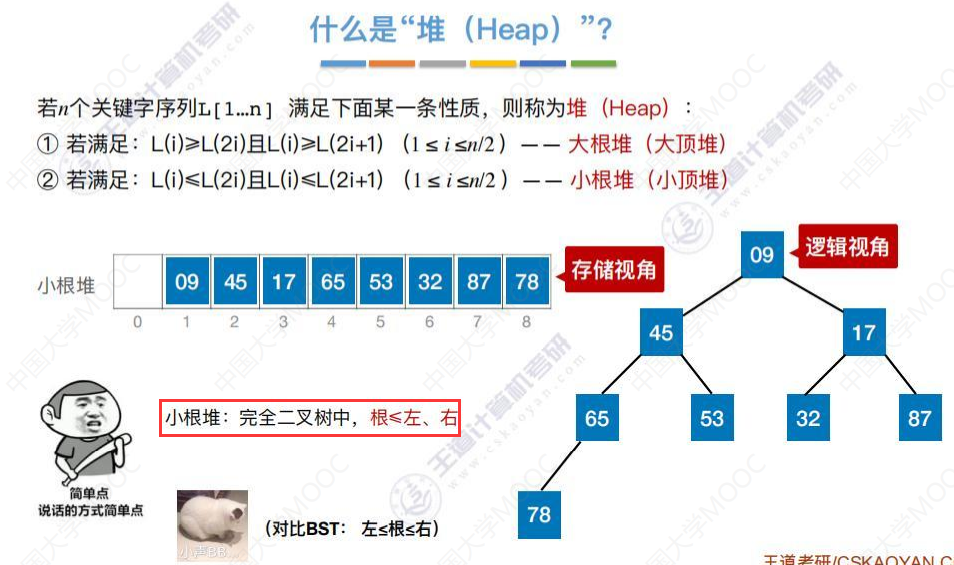
如何基于堆进行排序

建立大根堆
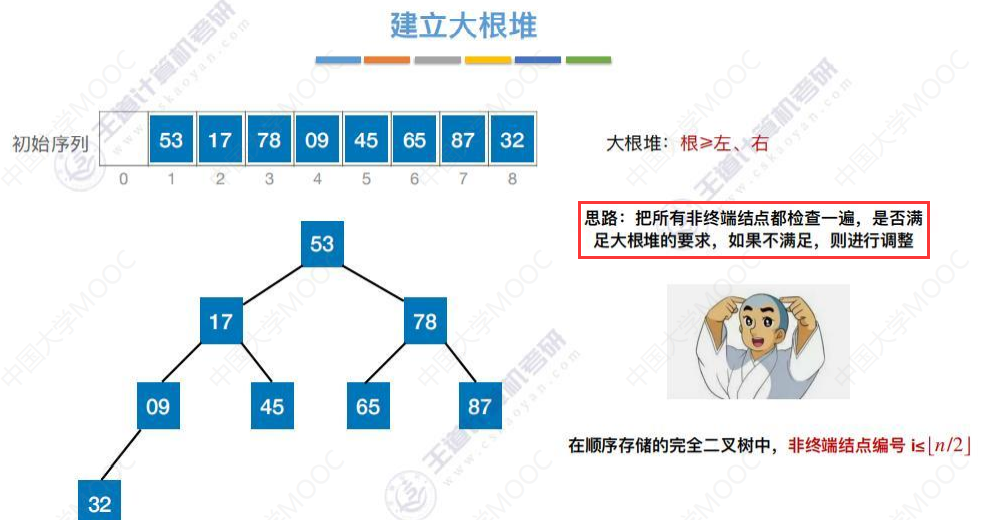
从n/2 的位置 8/2即4的位置开始逐个往前检查。
9不大于他的左孩子32,互换位置。
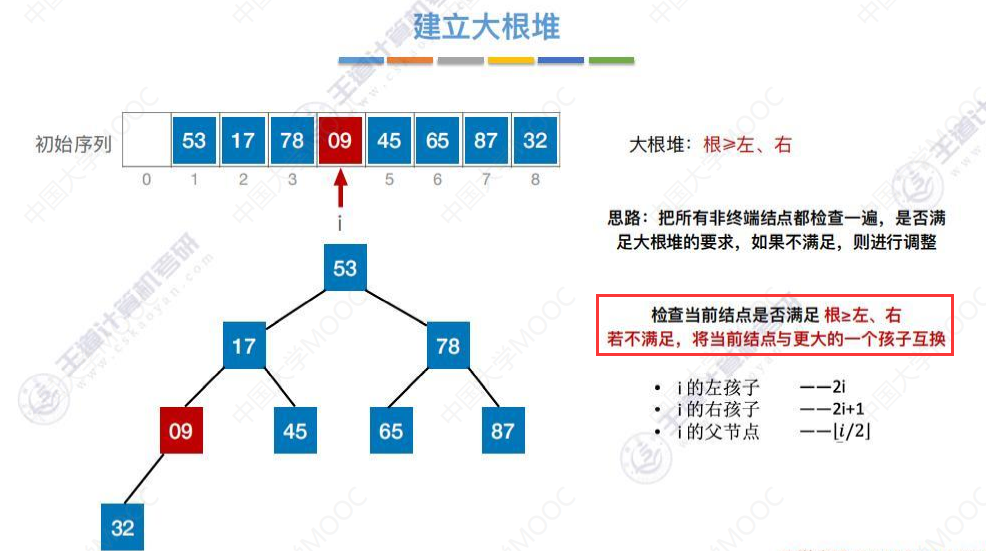
互换后符合大根堆
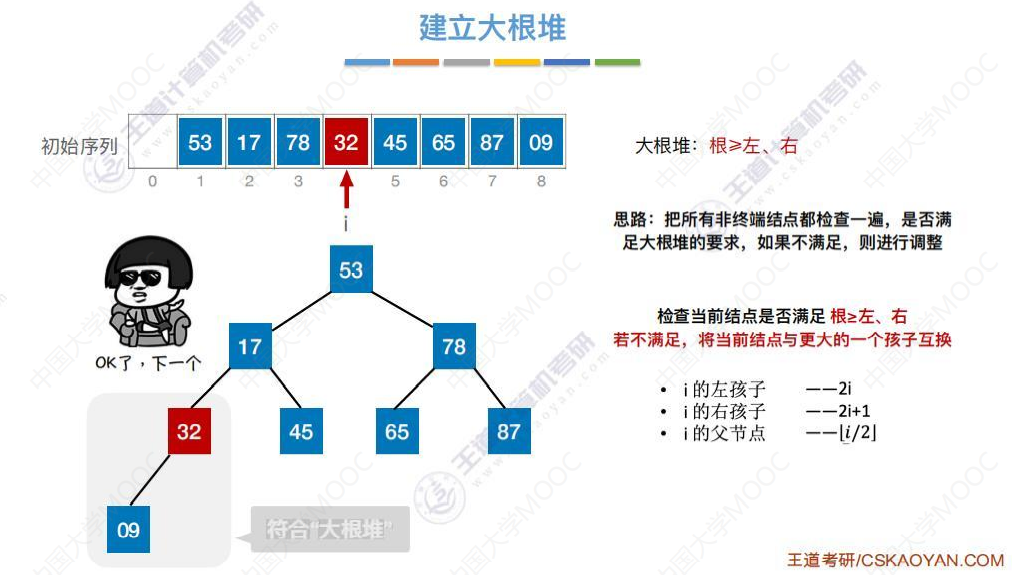
检查78,78小于右孩子87,互换位置。
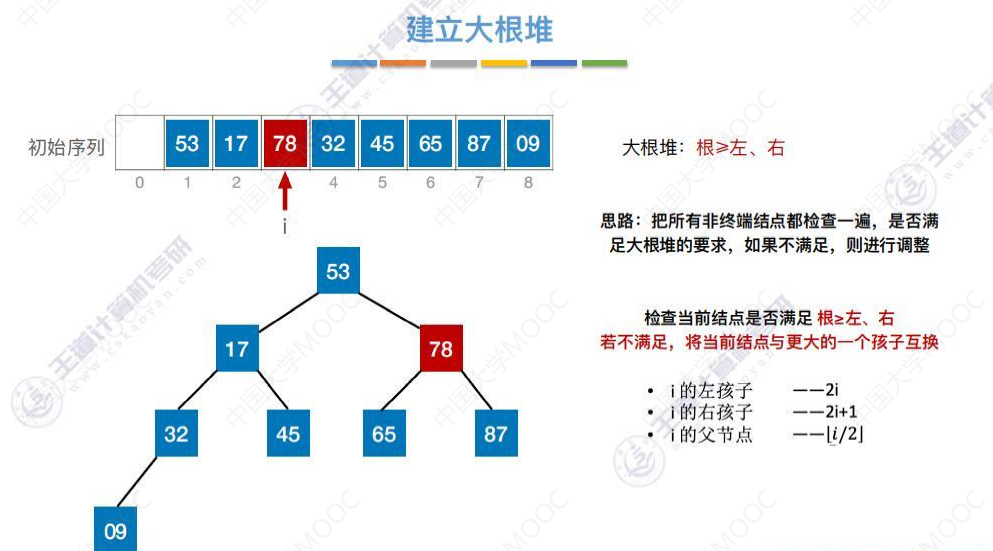
交换位置后符合大根堆
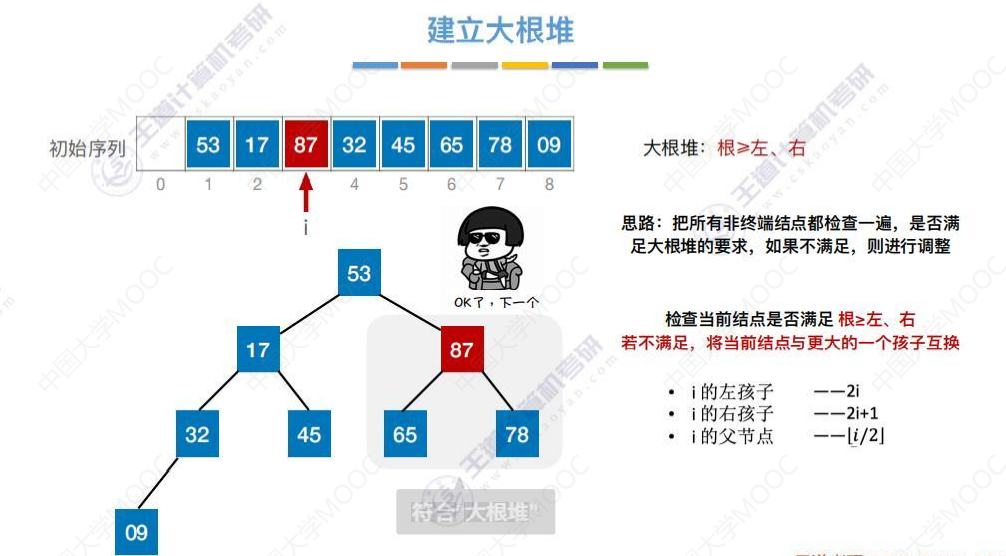
检查17,17小于右孩子45,互换位置
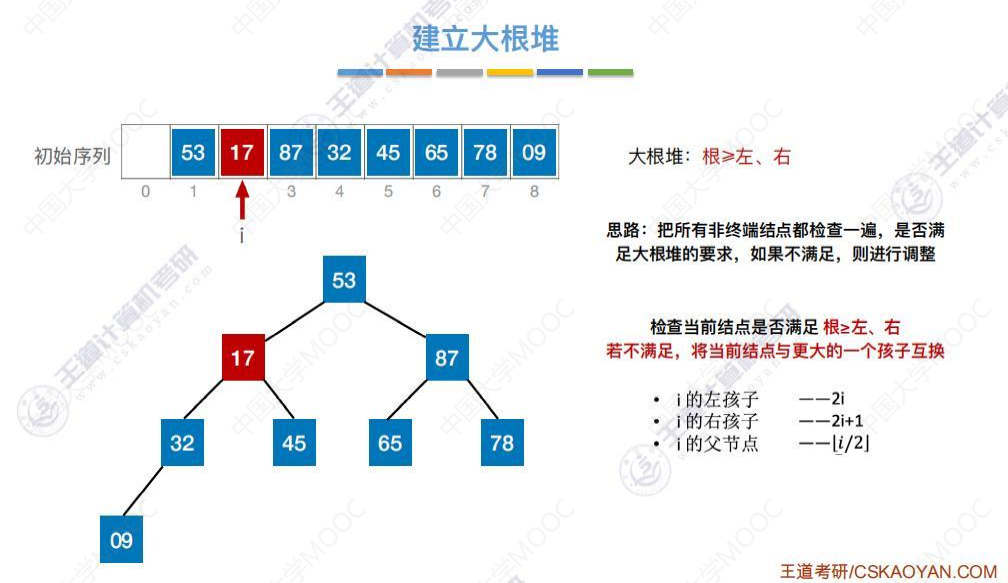
交换位置后符合大根堆
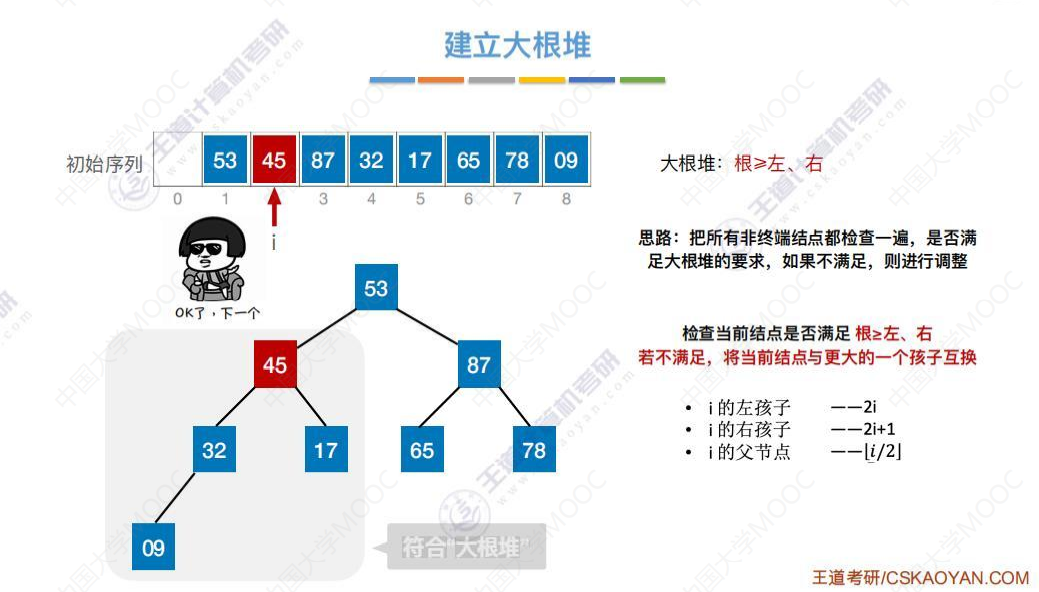
检查53,53小于其右孩子87
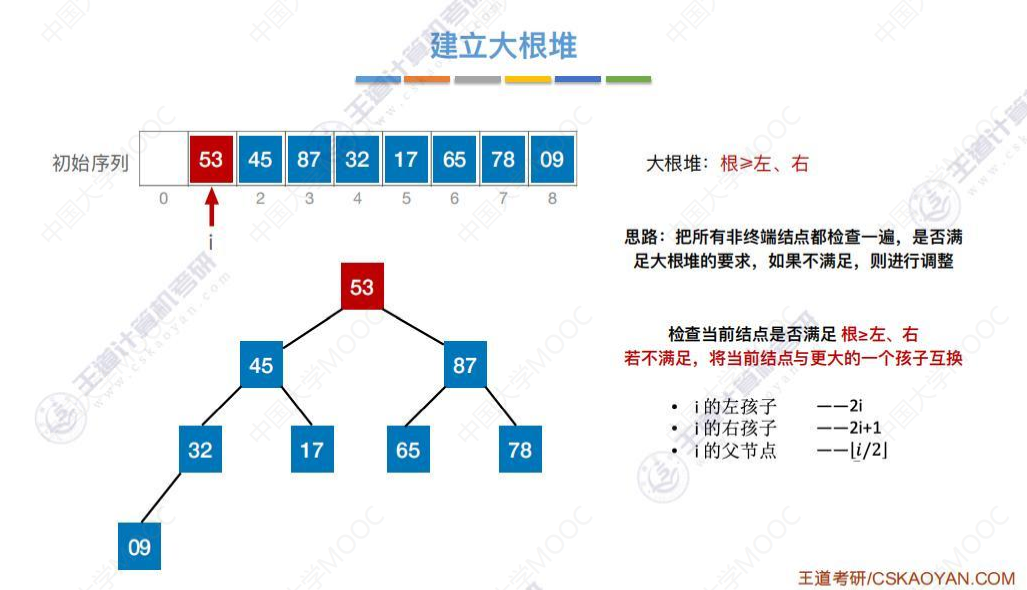
交换位置后,53引起了其下层子树不符合大根堆要求,
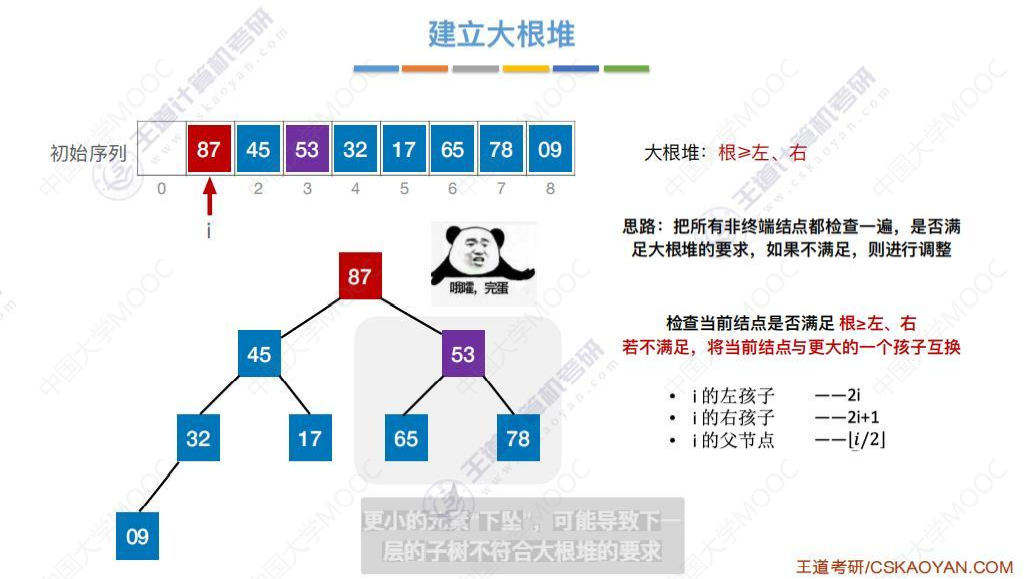
采取同样的方式检查53,53小于其右孩子78,交换位置。
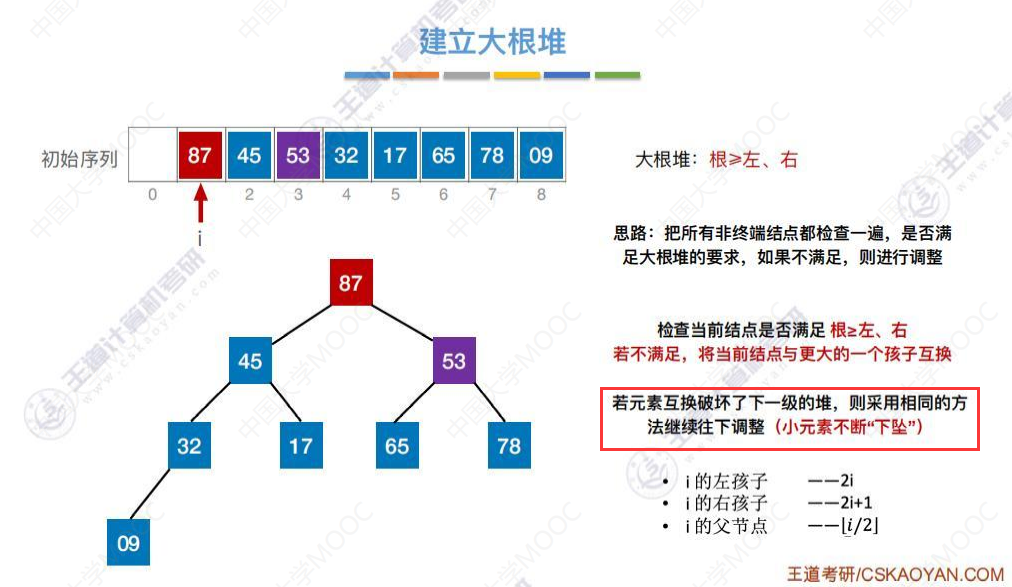
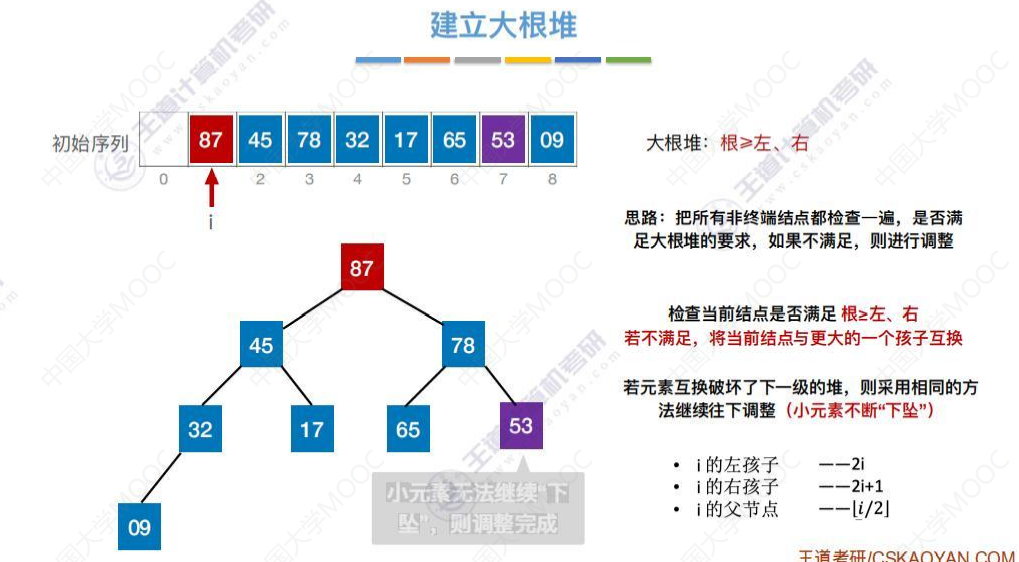
调整完成
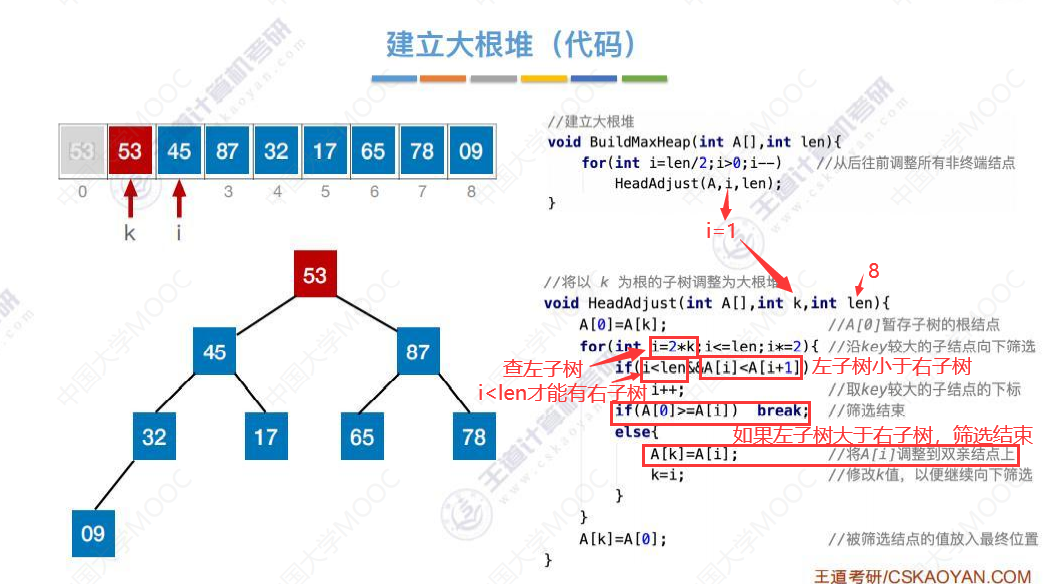
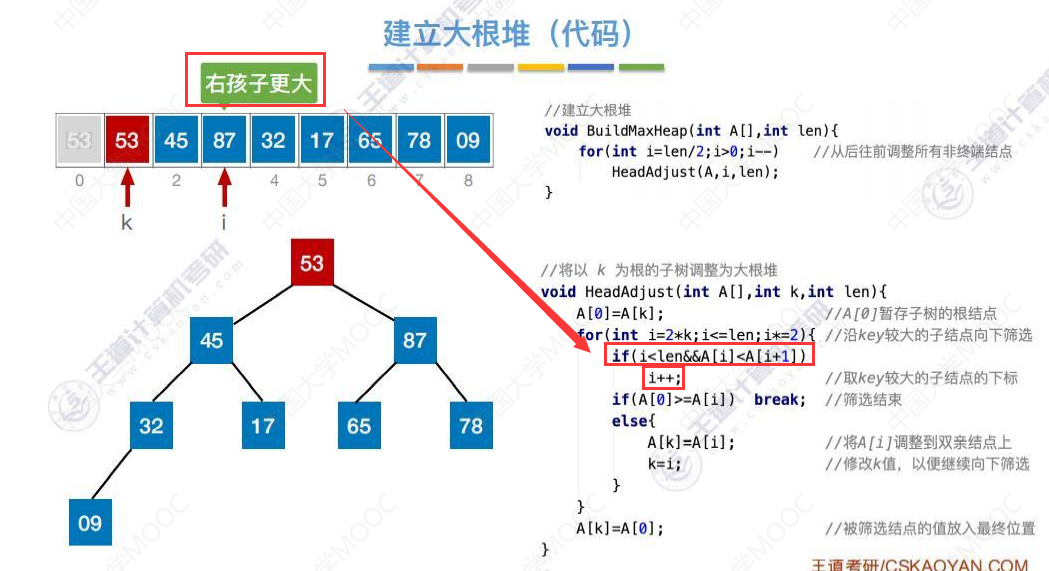
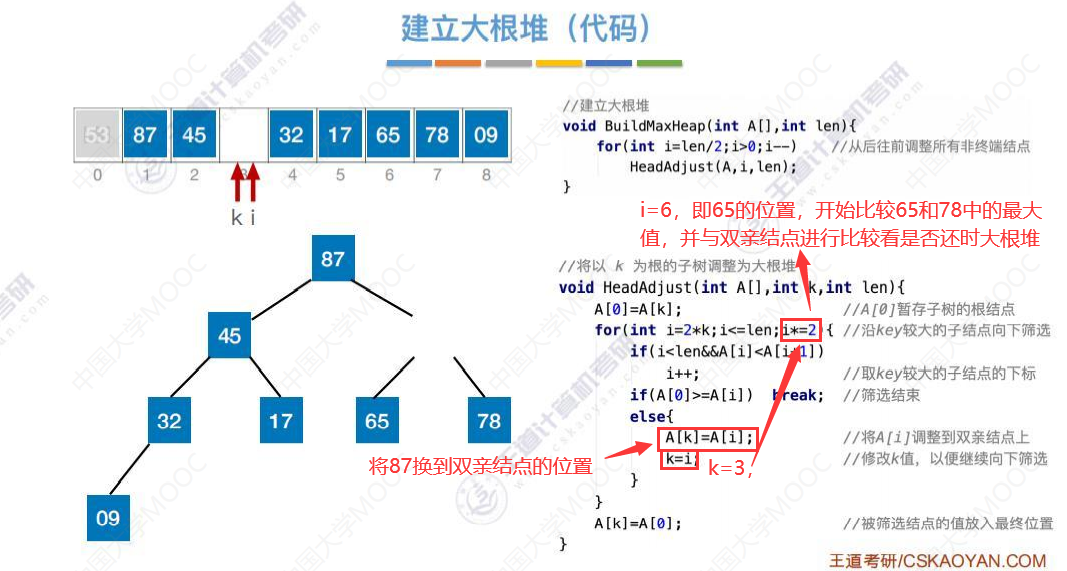
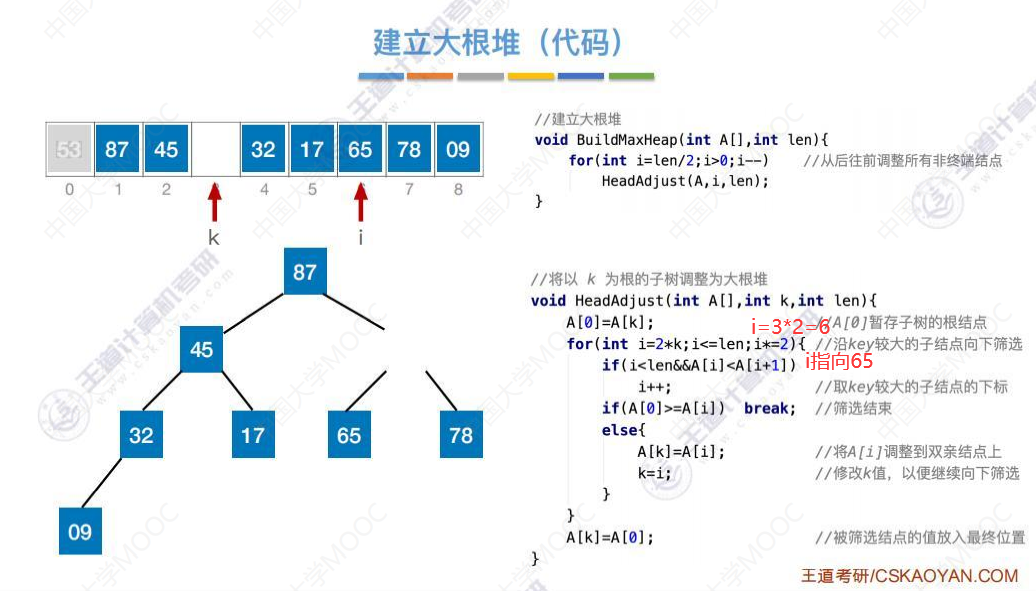
建立大根堆的代码
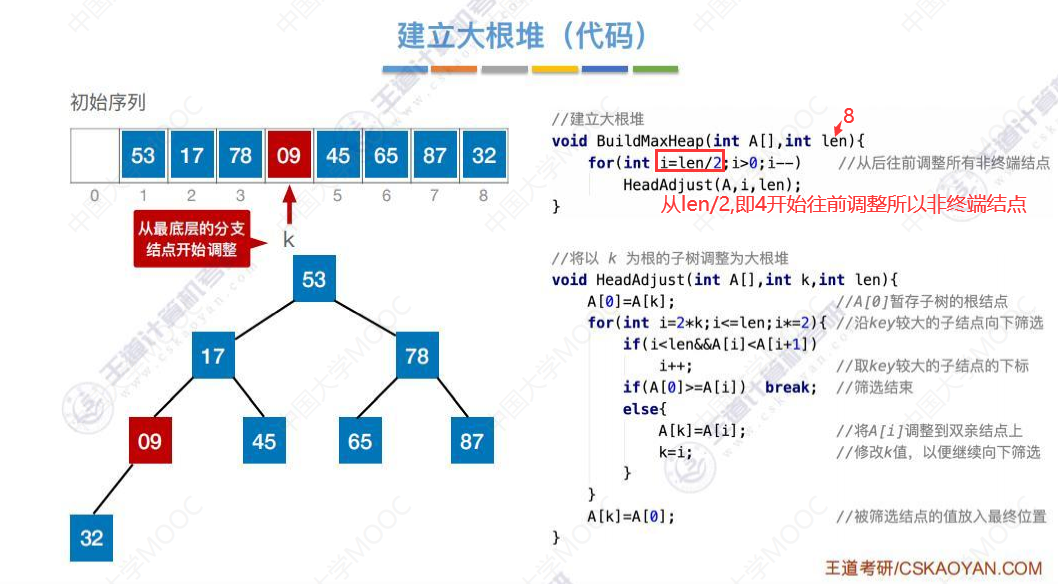
这里我们直接快进到代码执行到53这个元素。
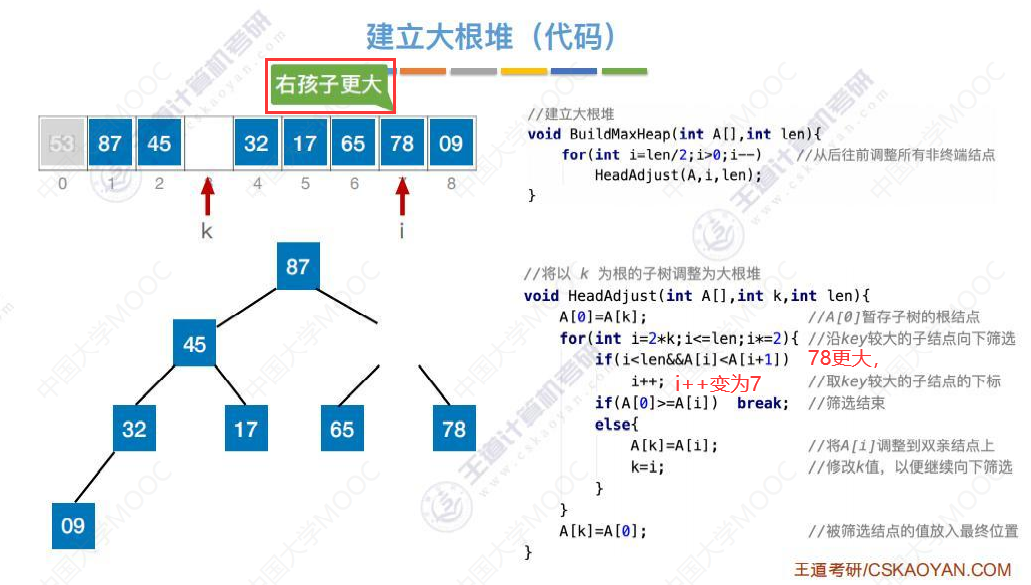
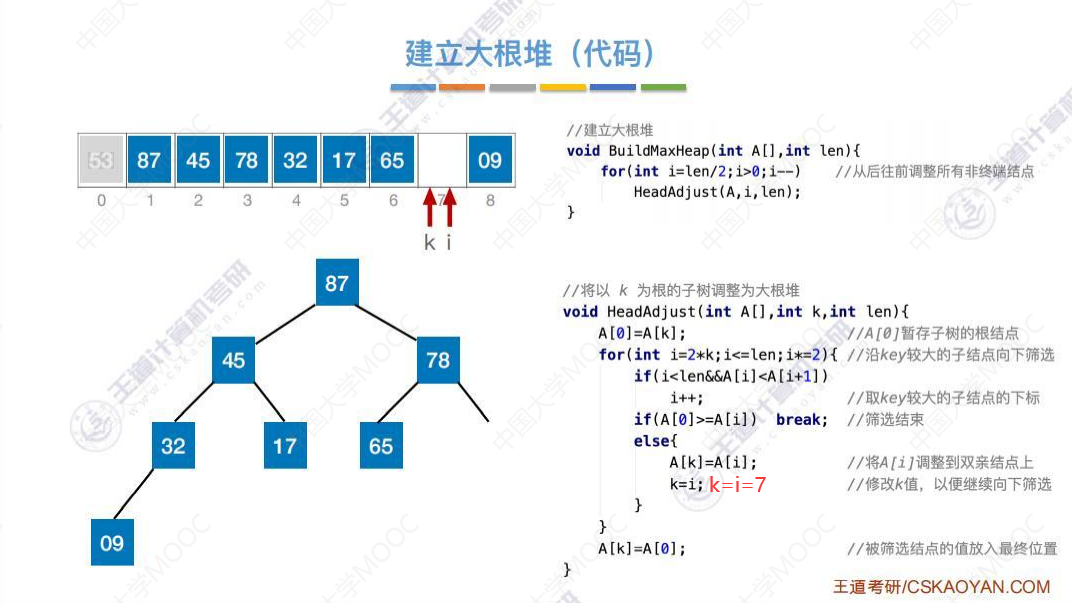
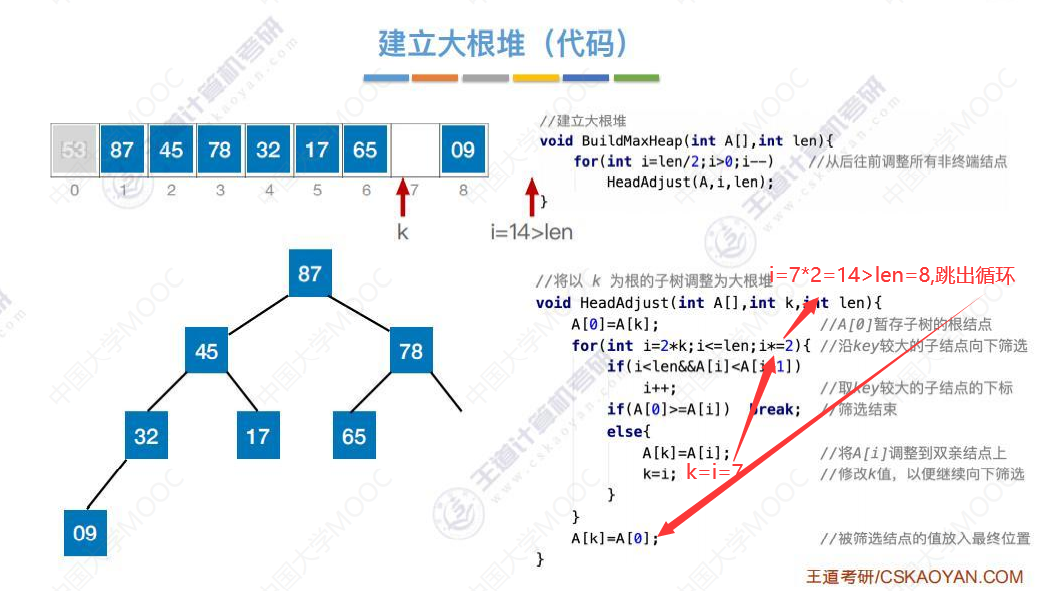
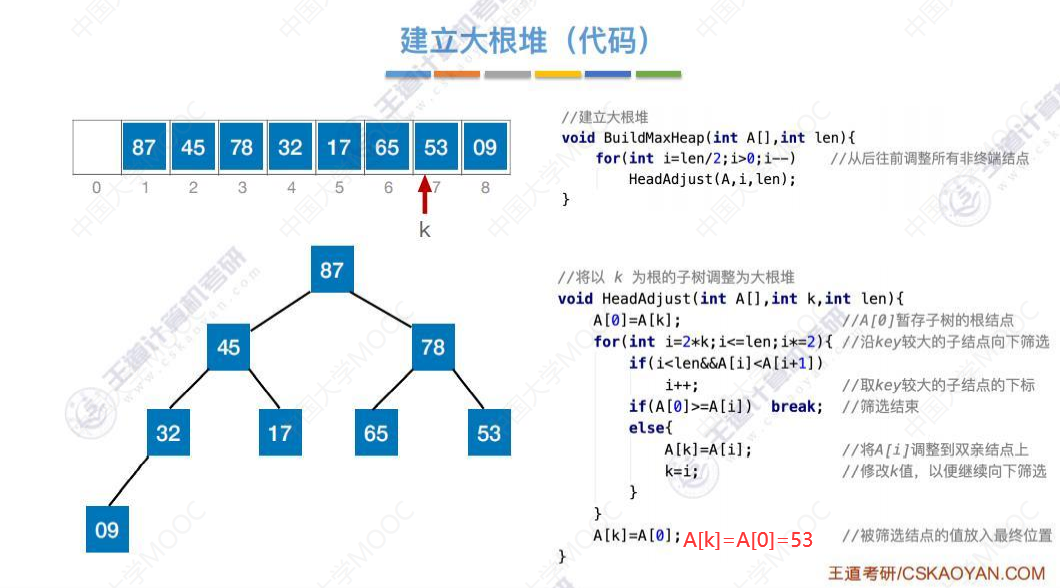
基于大根堆进行排序
将87与待排序序列的最后一个元素9交换
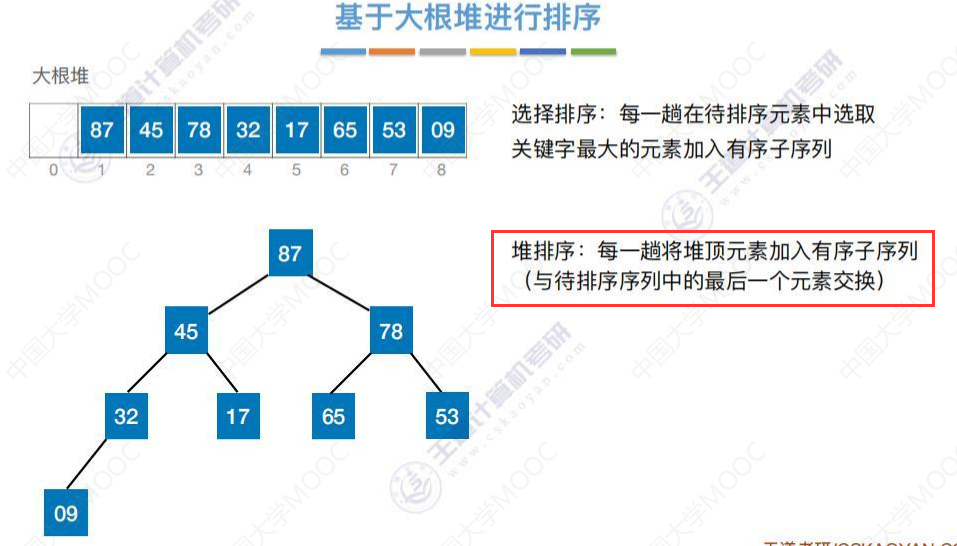
87和09交换完成,87不需要再移动
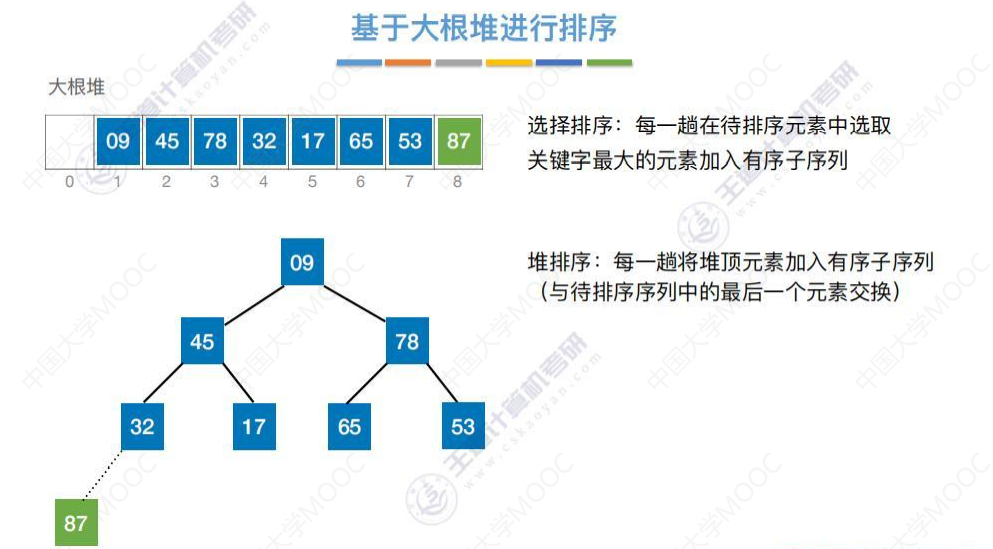
将待排序元素序列再次调整为大根堆
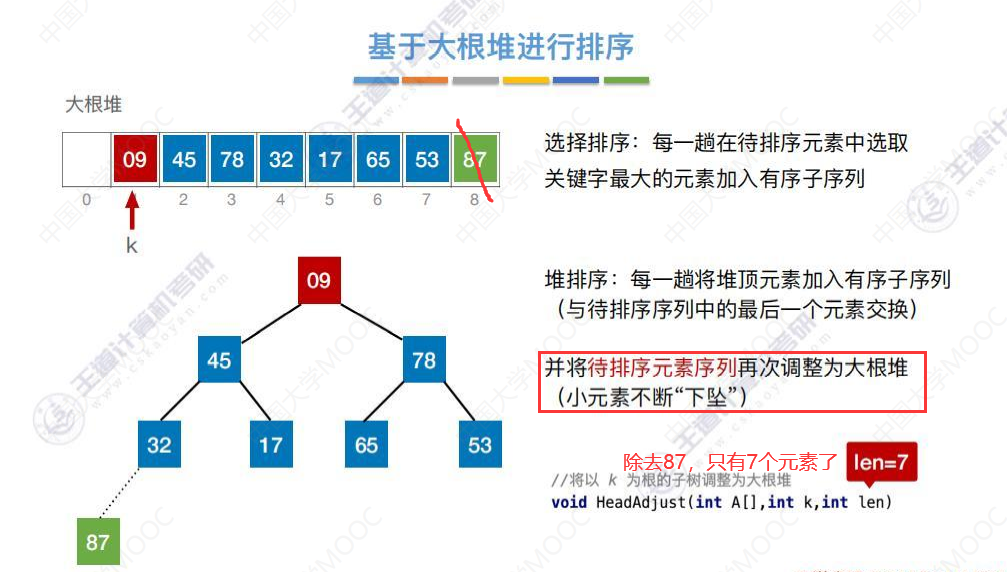
小元素09下坠第一次
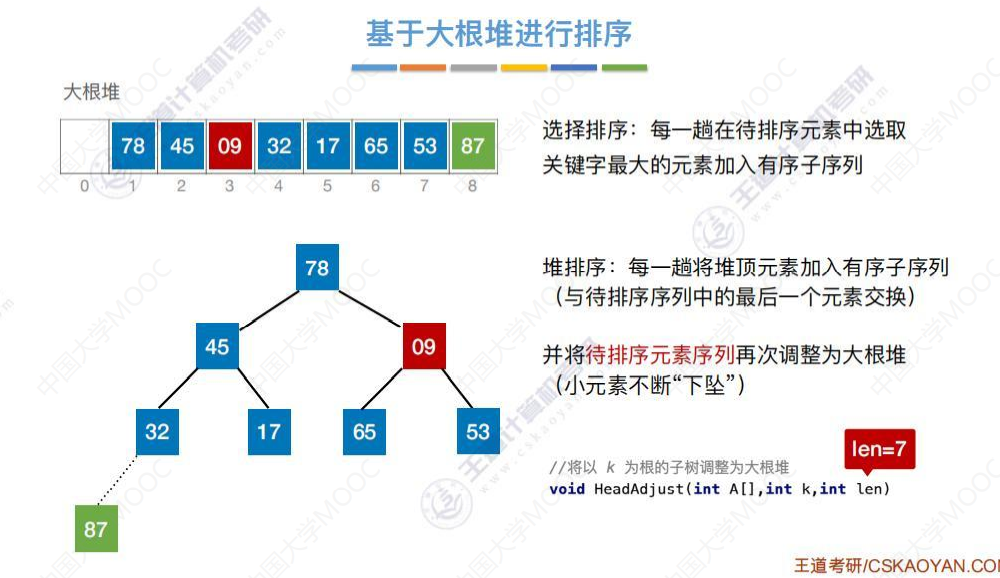
小元素09下坠第二次
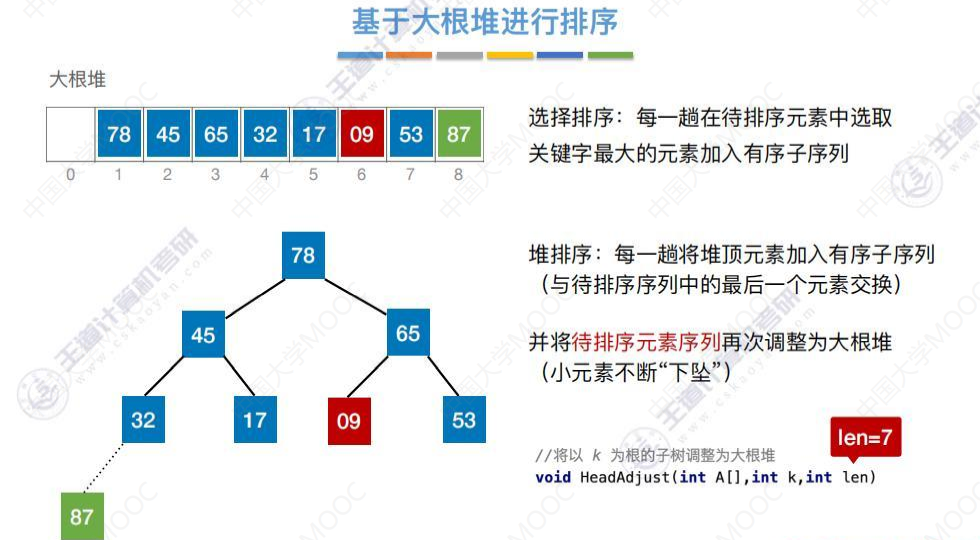
经过调整后待排序元素序列再次构成一个“大根堆”
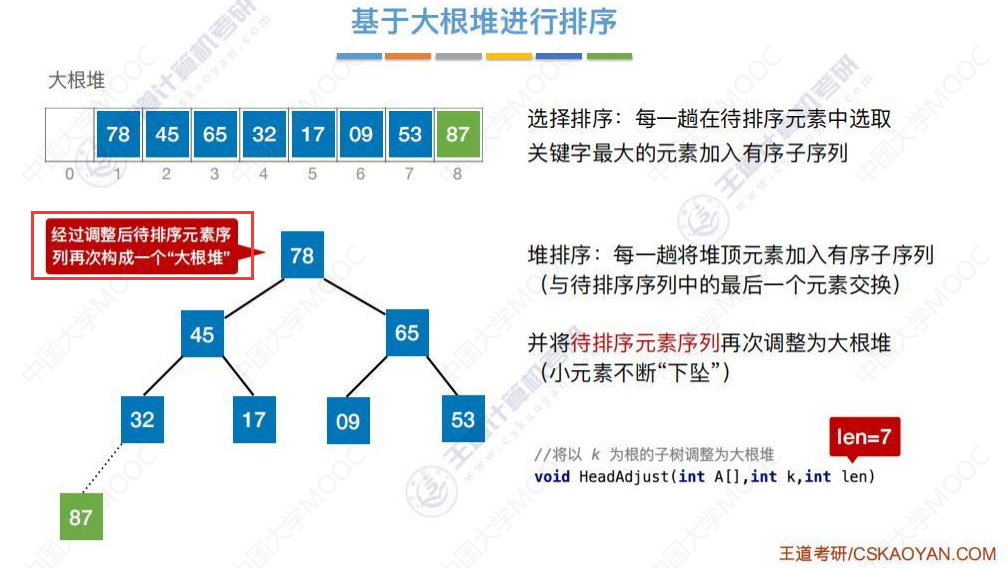
将78跟待排序序列的最后一个元素交换。
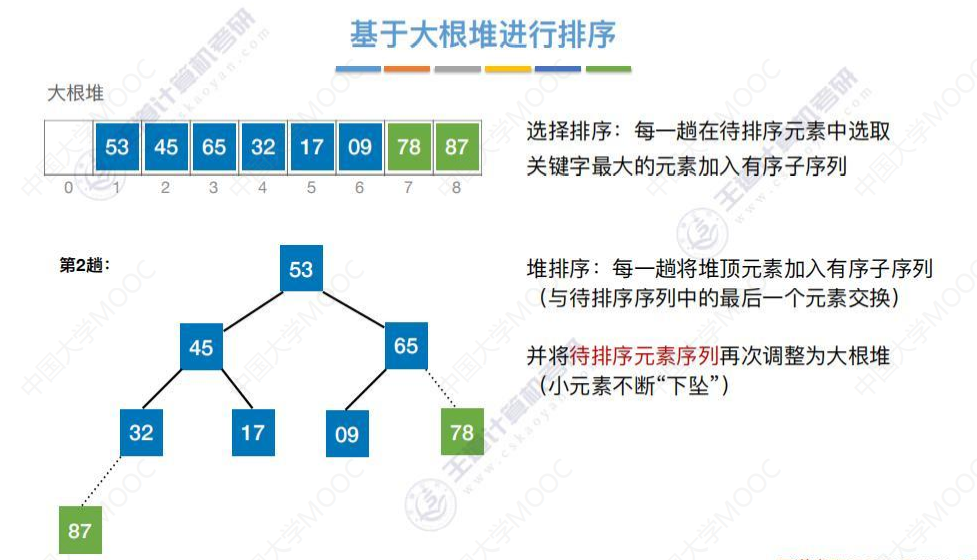
53被交换到第一个元素的位置
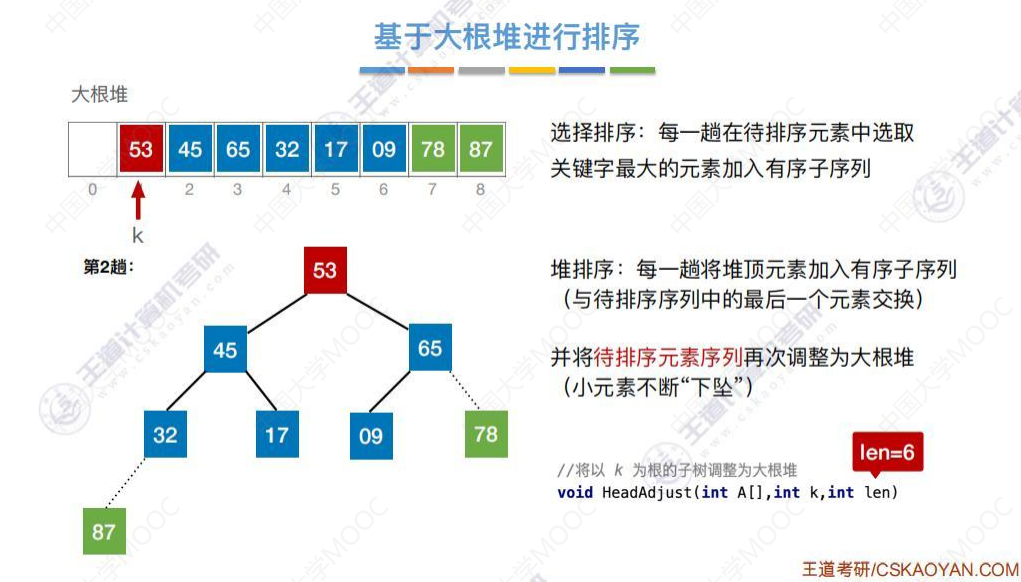
53下坠一次,由于78已经被排好序了,不在待排序序列中了,所以不用在比较53和78了,下图虚线的就不用再比较了。

经过调整后待排序元素序列再次构成一个“大根堆"
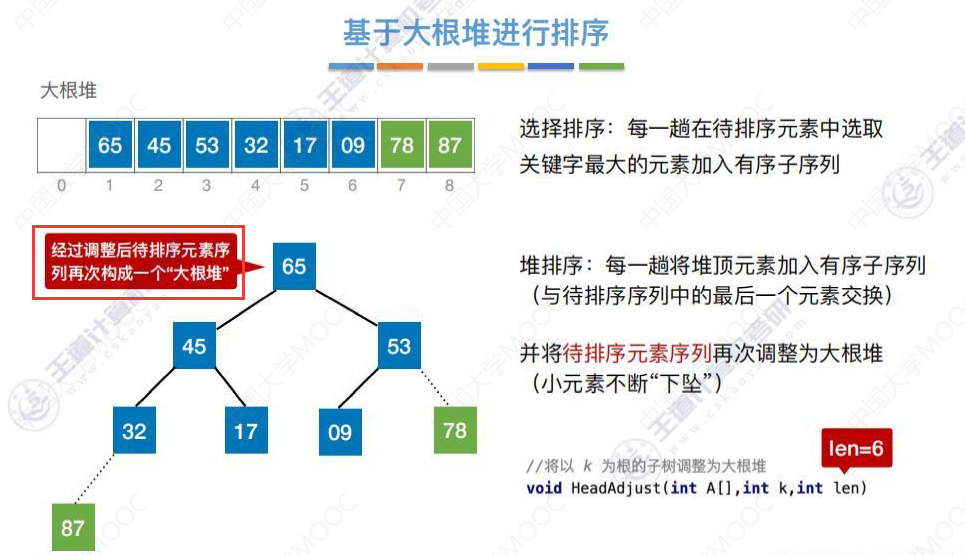
将65和待排序序列中的最后一个元素交换。
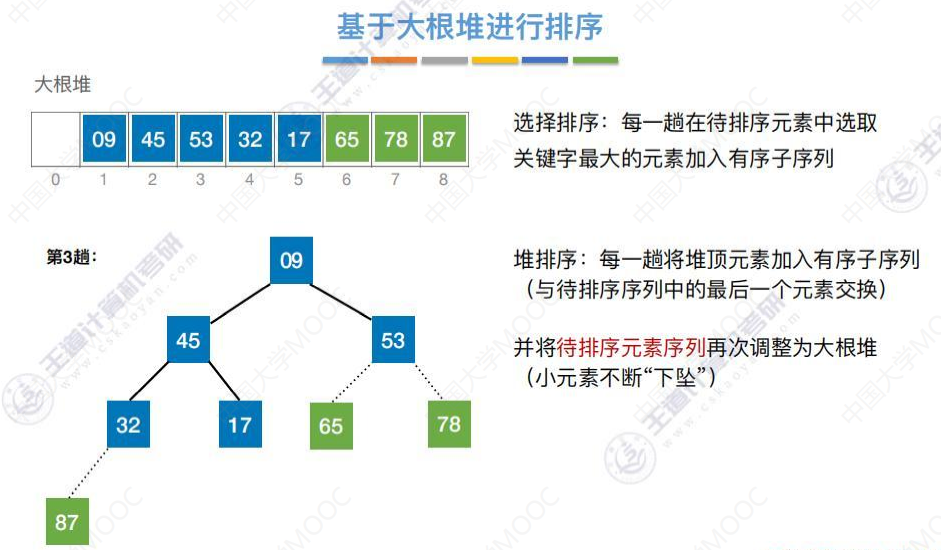
9被换到第一个位置,继续小元素下坠
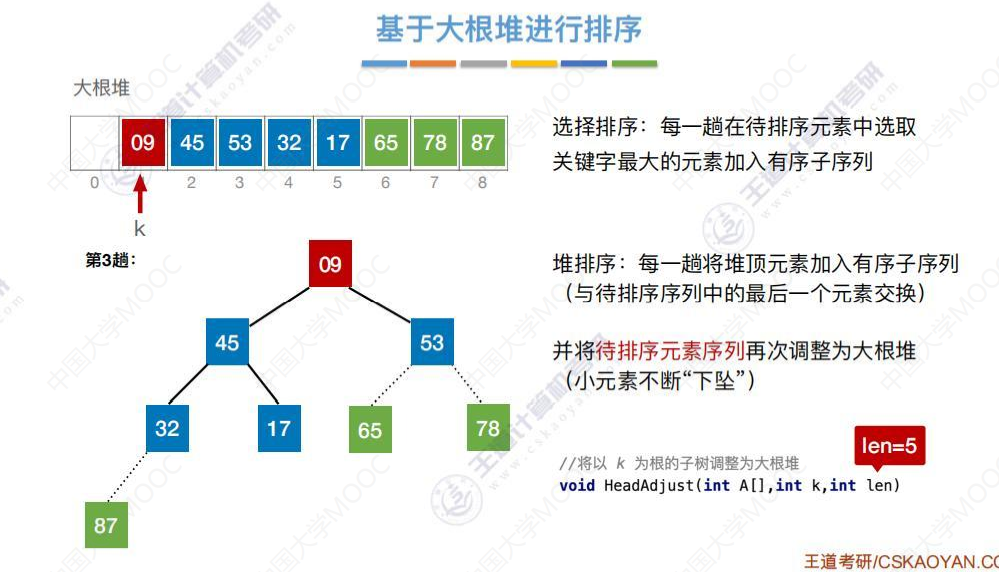
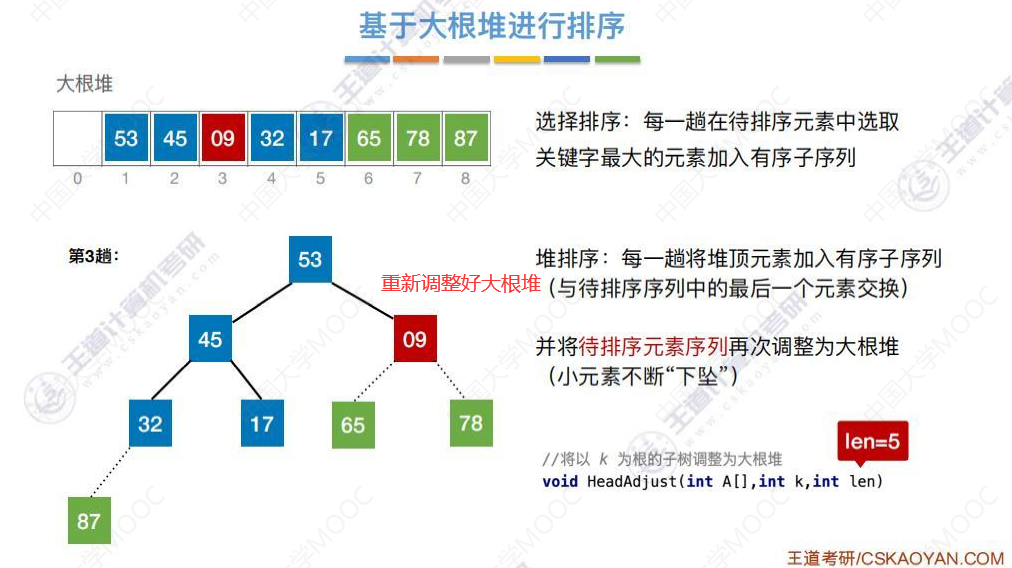
将53与待排序序列中的最后一个元素交换,
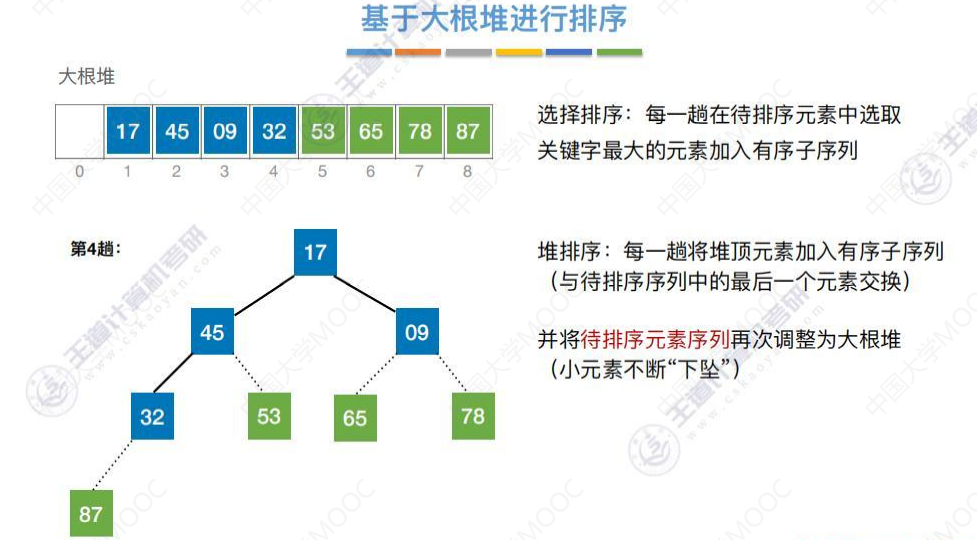
将17进行下坠
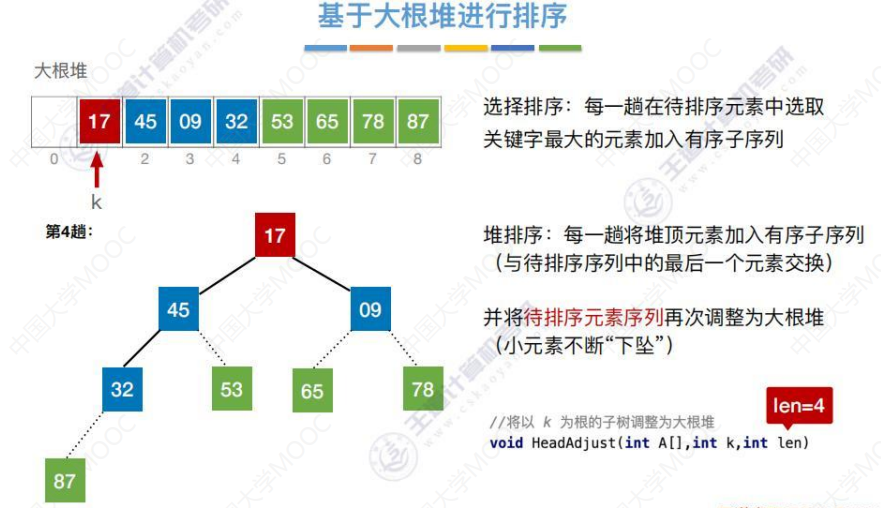
17下坠一次,还没形成大根堆
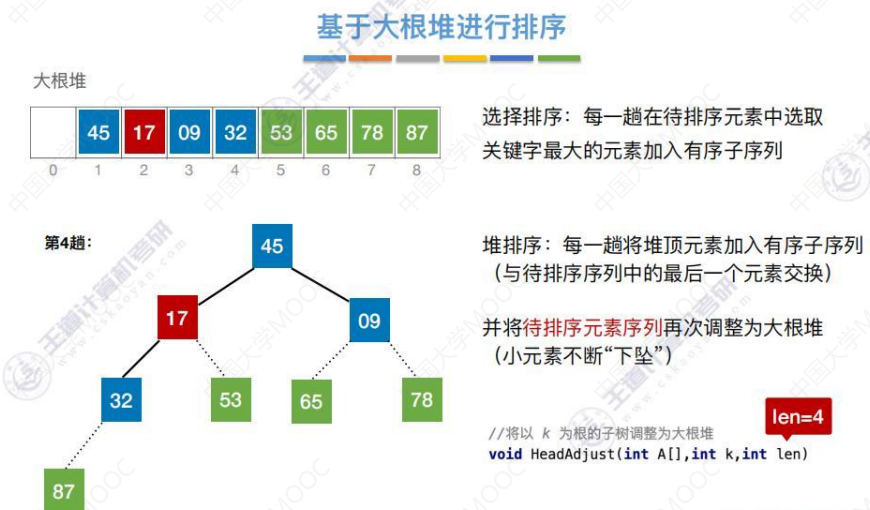
17下坠第二次,形成大根堆

将45和17进行交换,
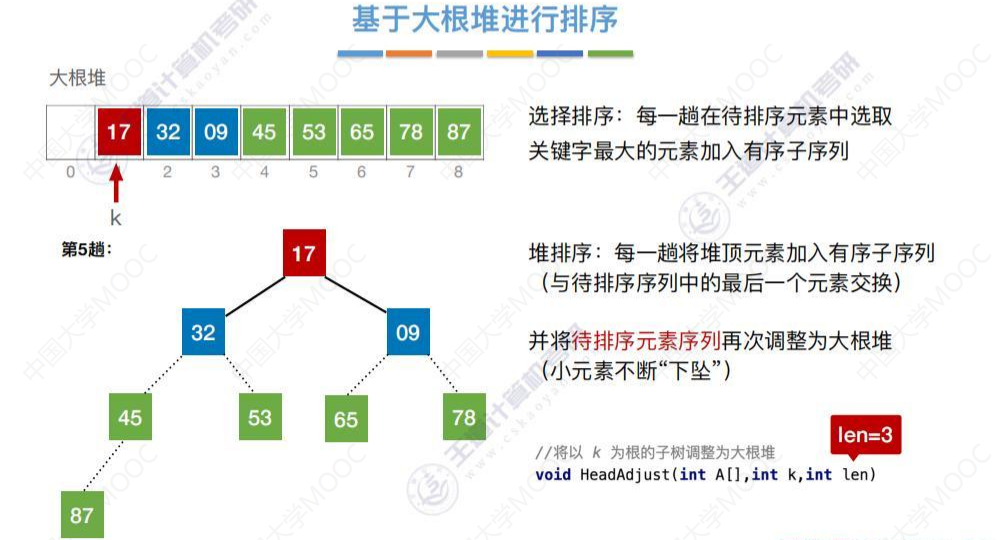
17下坠一次,形成大根堆
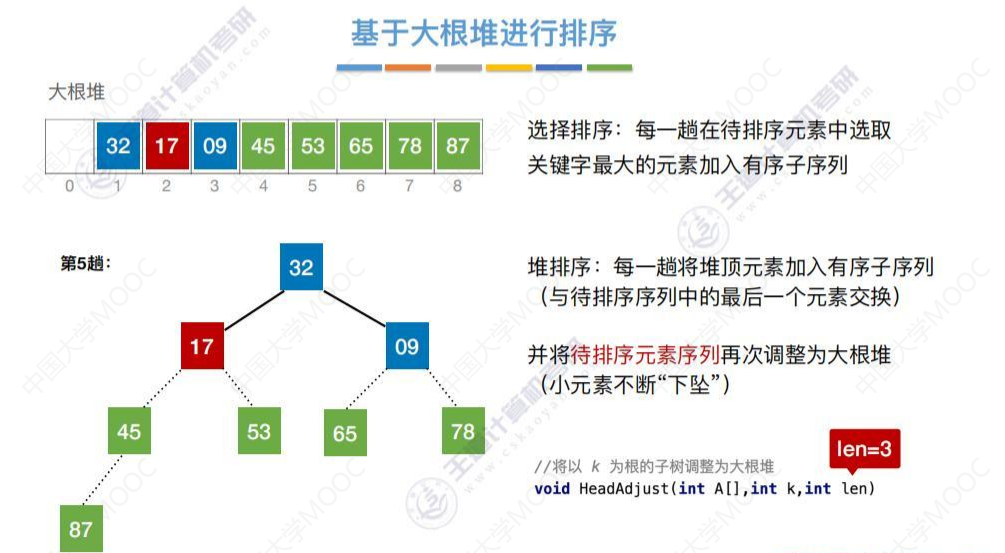
将来32和9交换,
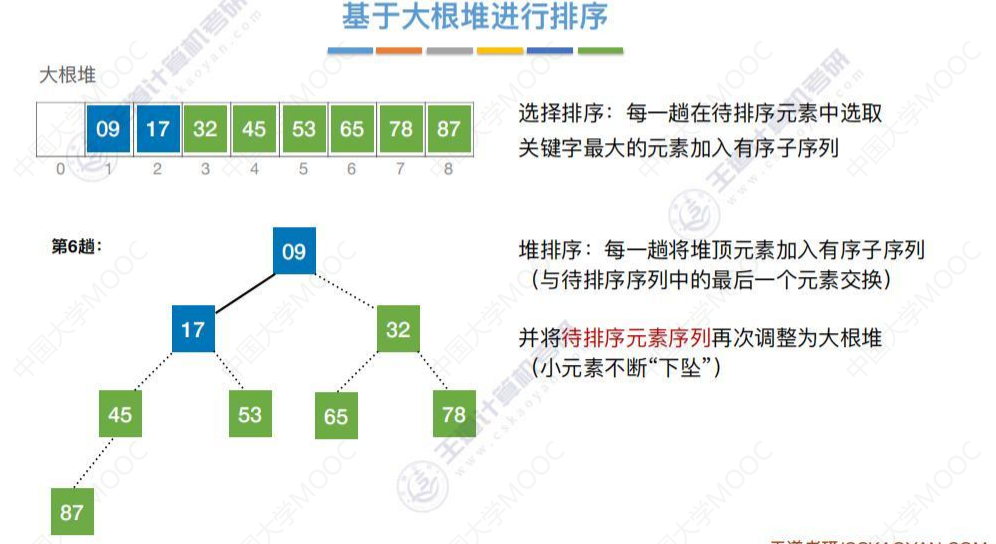
9下坠一次形成大根堆
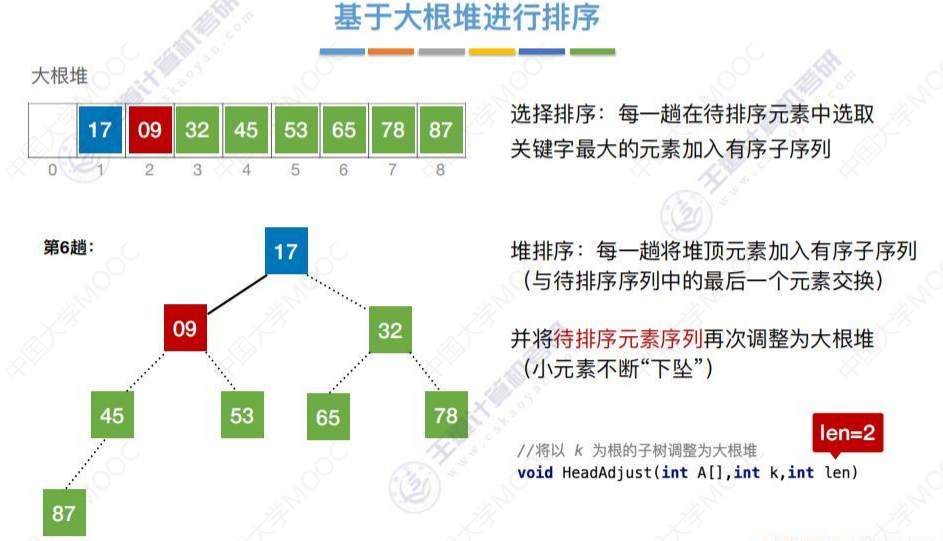
将17和待排序元素序列中的元素9交换,只剩下一个元素9,不用再调整。
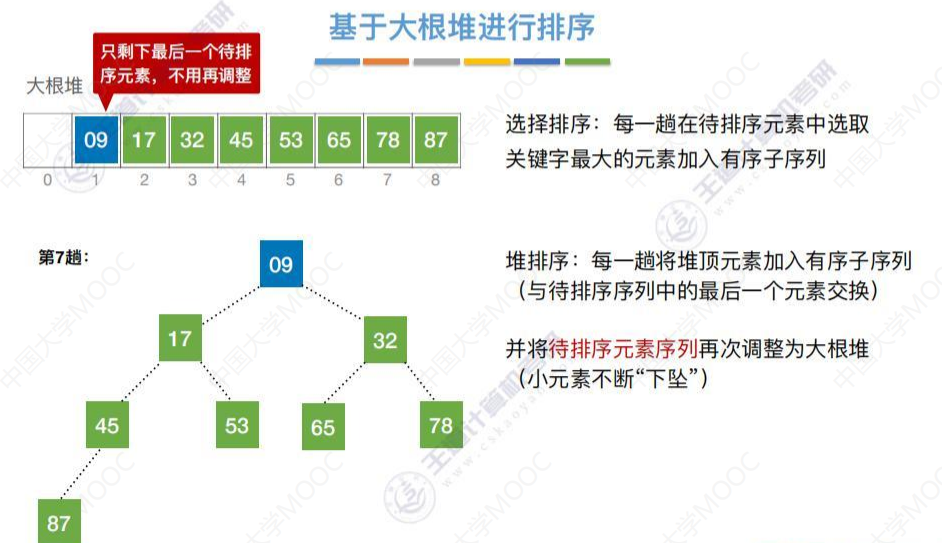
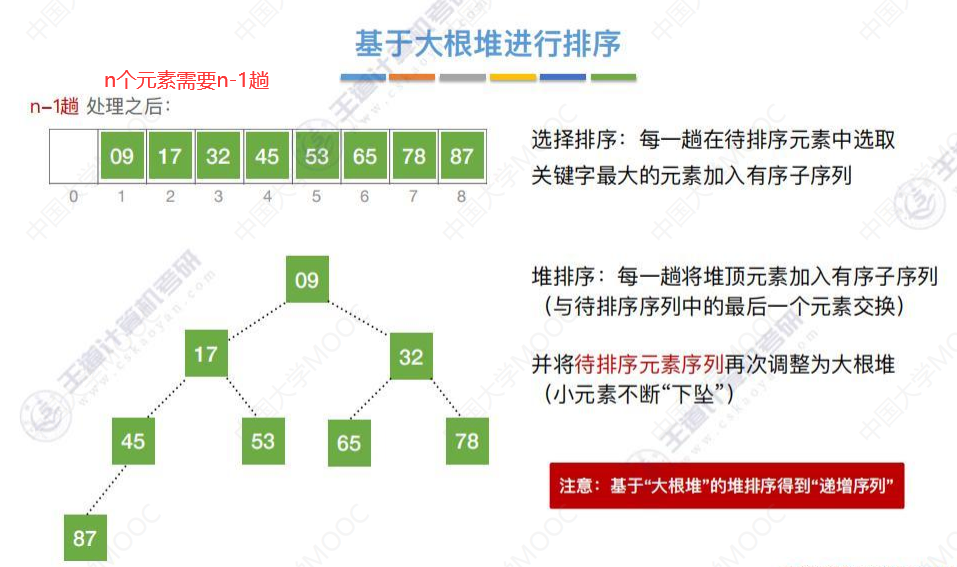
基于大根堆进行排序(代码)
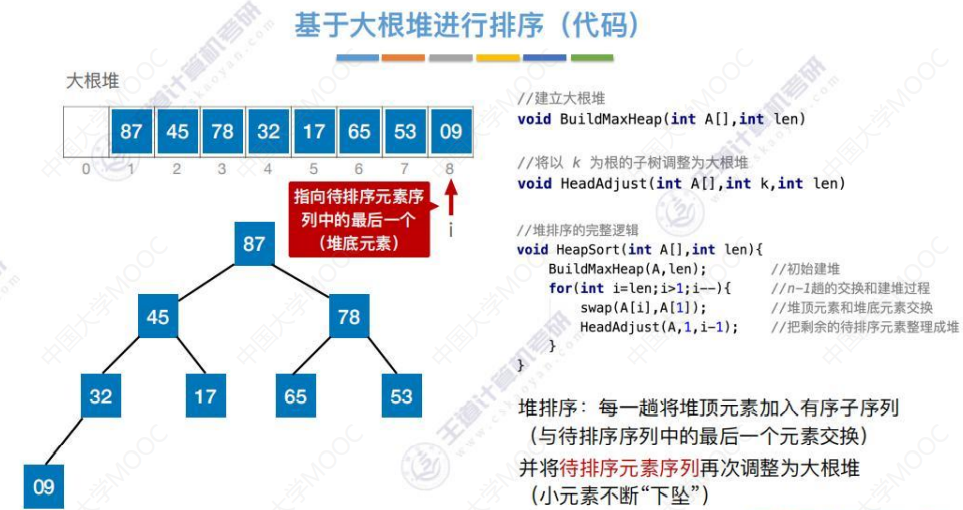

算法效率分析
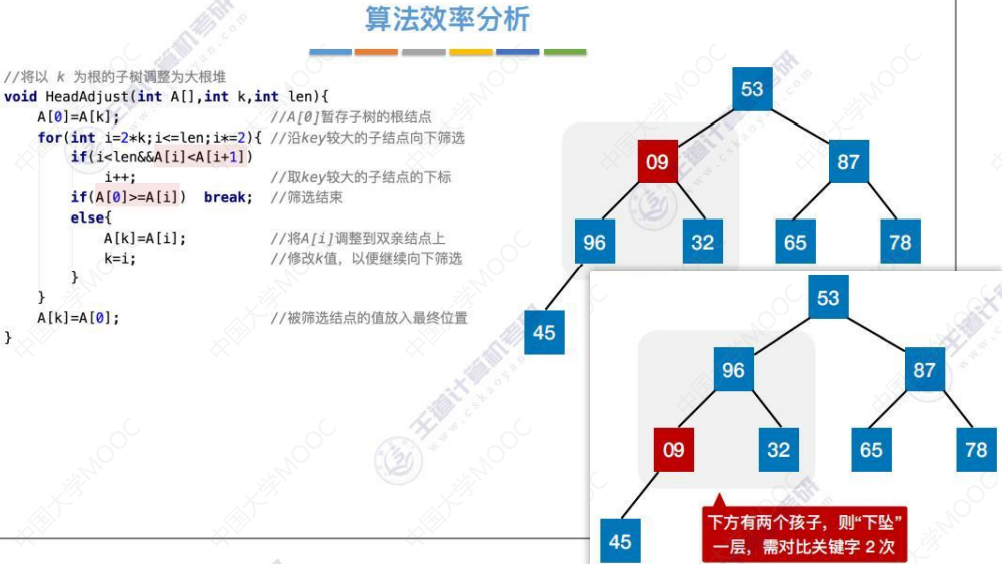
下方有两个孩子,则“下坠”一层,需对比左右孩子各1次
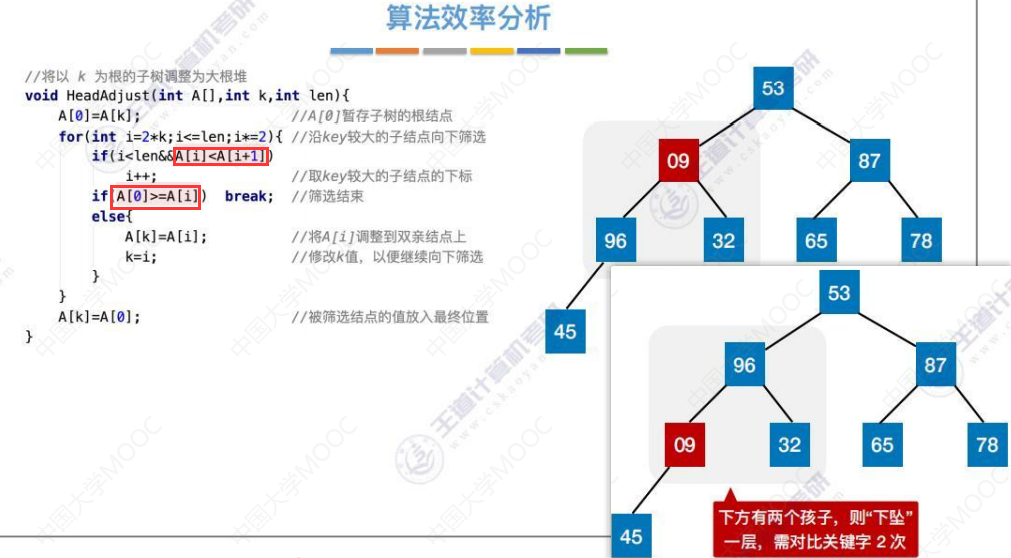
下方只有1个孩子,则“下坠”一层,需对比左孩子1次。i<len说明没有右孩子。
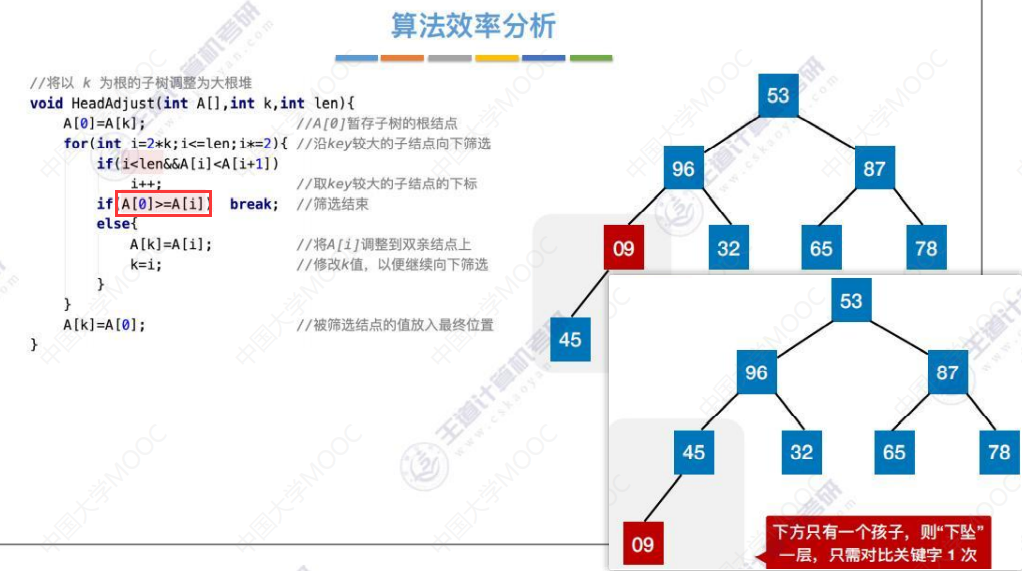
时间复杂度1:建堆的过程(每个关键字都可能下坠)
第1层有1个结点,最多下坠(h-1)层,每个结点最多对比关键字不超过2(h-1)
第2层有2个结点,最多下坠(h-2)层,每个结点最多对比关键字不超过2(h-2),第二层最多对比关键字不超过22(h-2),
第h层不下坠,
第h-1层有2的h-2次方个结点,最多下坠1层,每个结点最多对比关键字不超过2,第二层最多对比关键字不超过22的h-2次方,


时间复杂度2:每一趟调整的过程(由于已经建完堆了,双亲结点大于孩子结点,所以将一个元素下坠,无需担心被调整上去的元素造成大根堆的破坏,只需要考虑下坠元素即可,而下坠元素最多下坠次数 不会超过树的高度h)

空间复杂度:只用到了几个 i 这样的变量,所以是常数级O(1)

稳定性分析


2杠和最后一个2交换,

未破坏大根堆,将第一个2和1交换,

还剩一个元素1,算法结束。结果显示是不稳定的。

8.4-3 堆的插入删除
插入
插入13
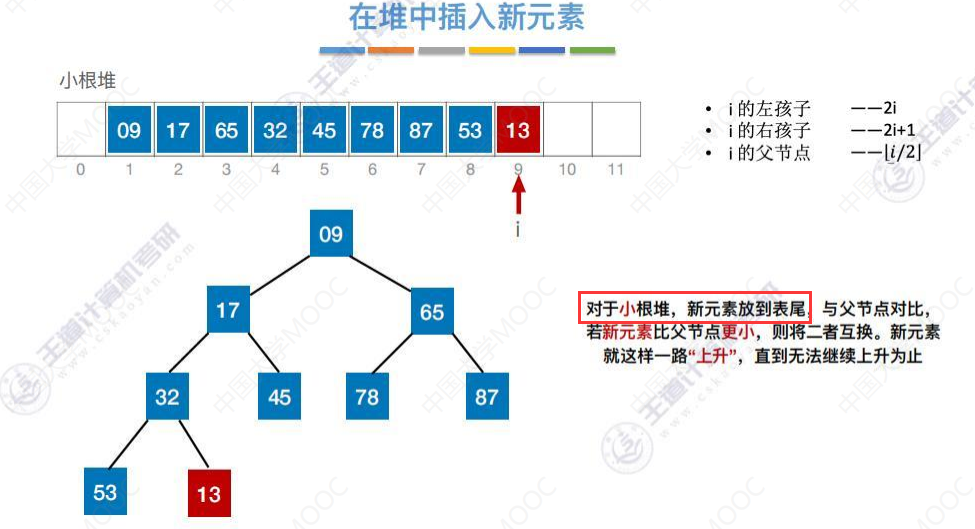
13和32比较一次,上升一层,

13和17比较一次,上升一层,17和9比较一次,17>9,无法上升,程序停止。共比较了3次关键字。
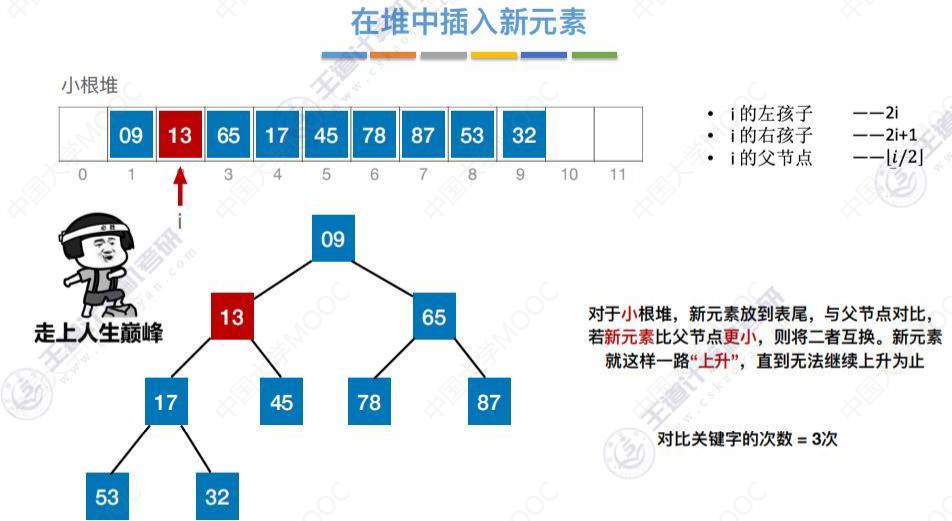
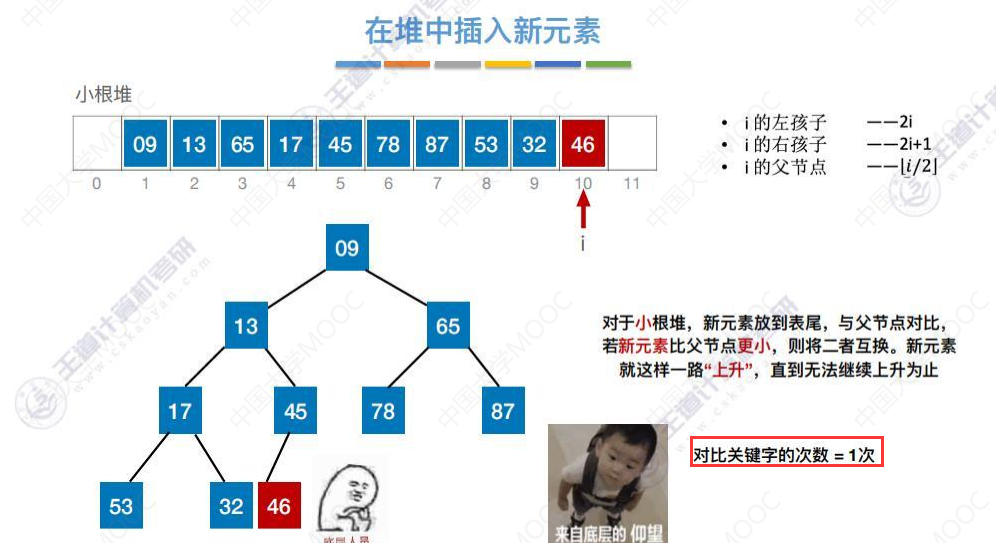
插入46
删除
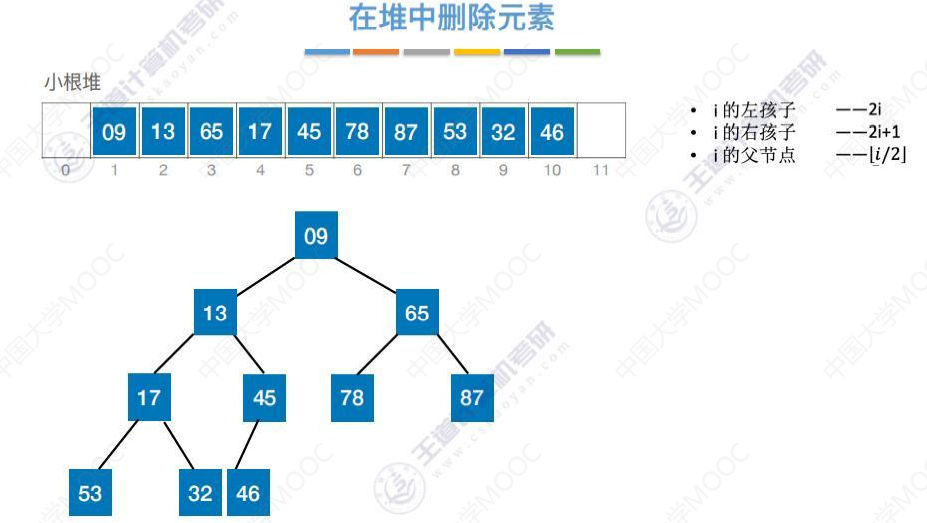
删除13,
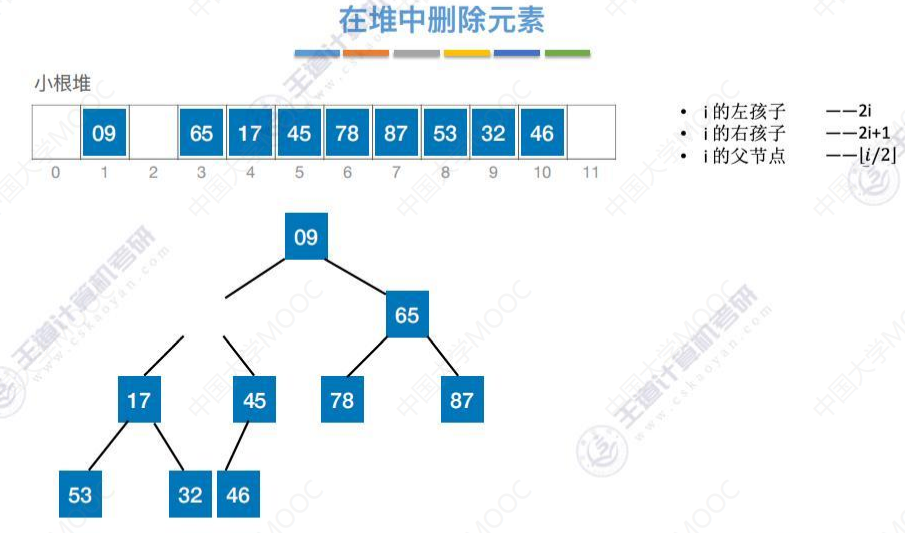
用堆底元素46替代被删除元素的位置。
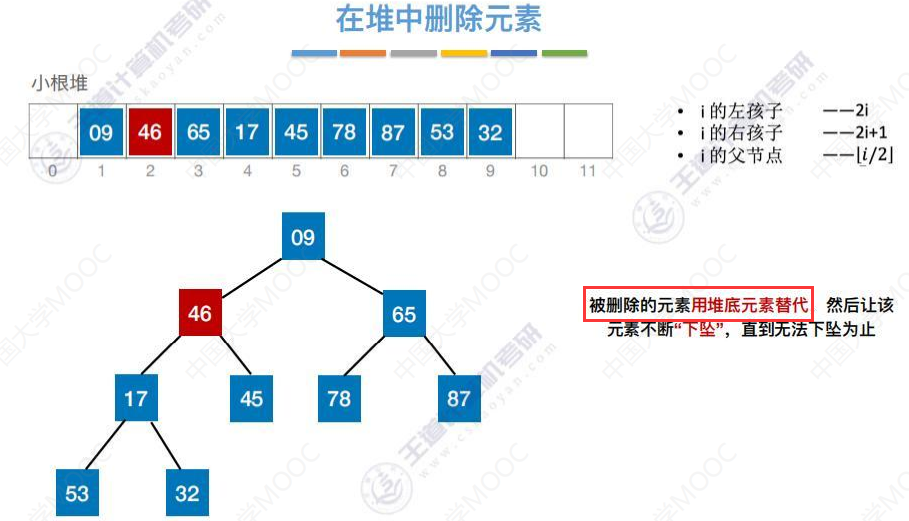
46下坠第一次,比较左右孩子各一次
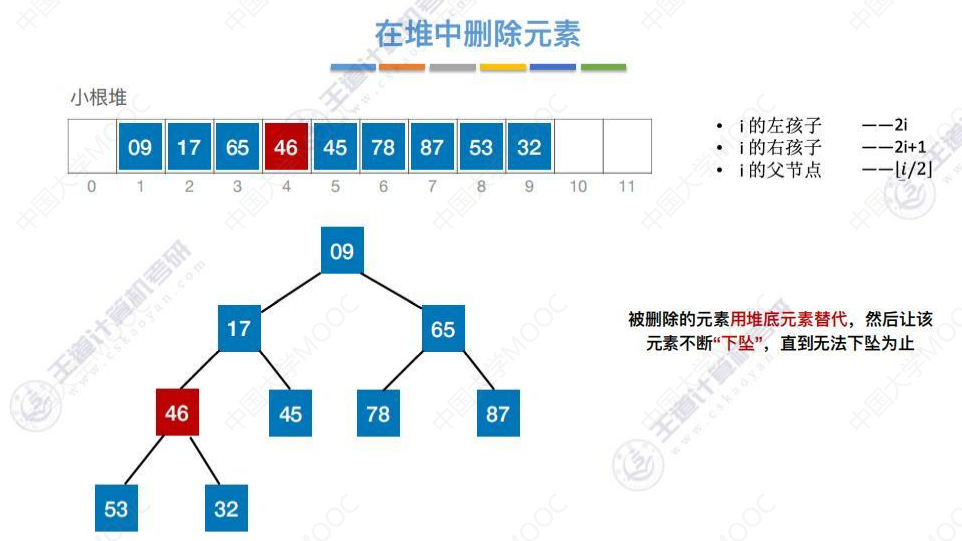
46下坠第二次,比较左右孩子各一次。以上共对比关键字次数4次
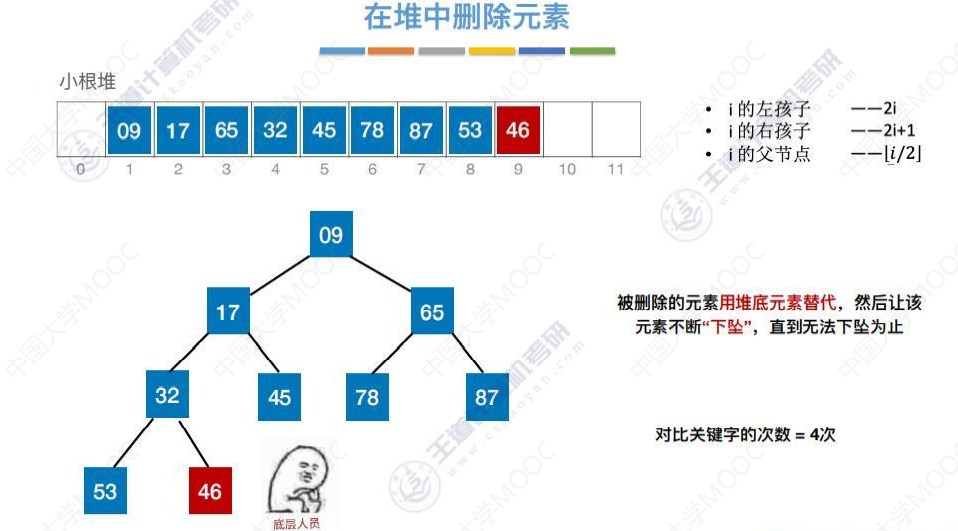
关键字对比次数

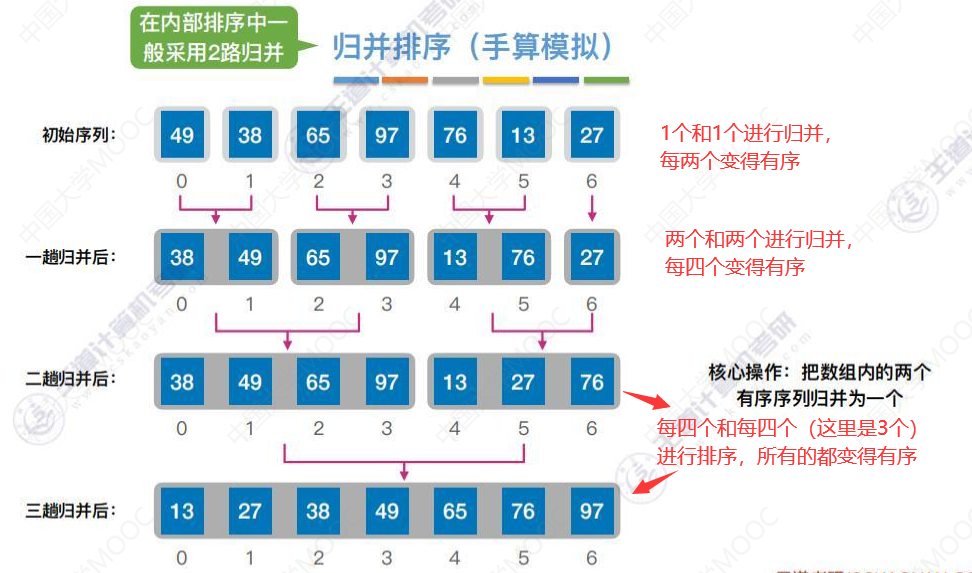
8.5-1 归并排序
什么是归并?


2路归并和4路归并
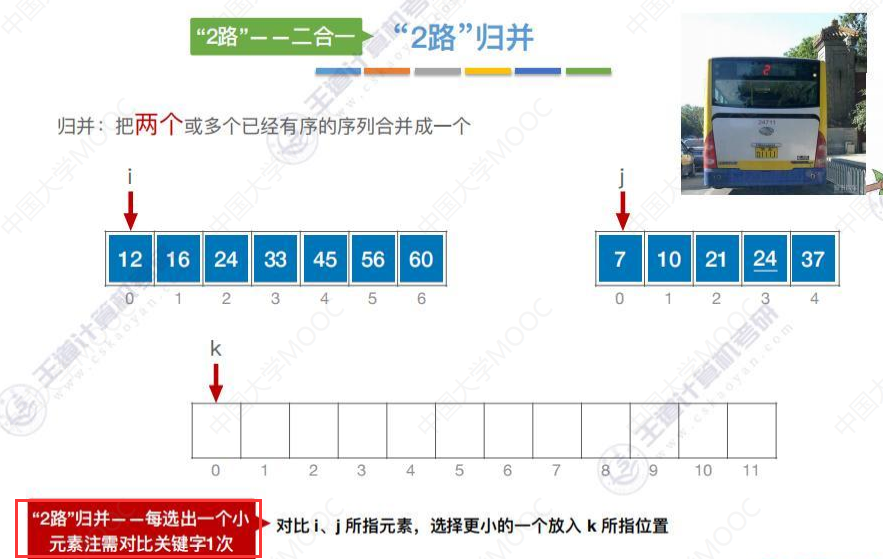
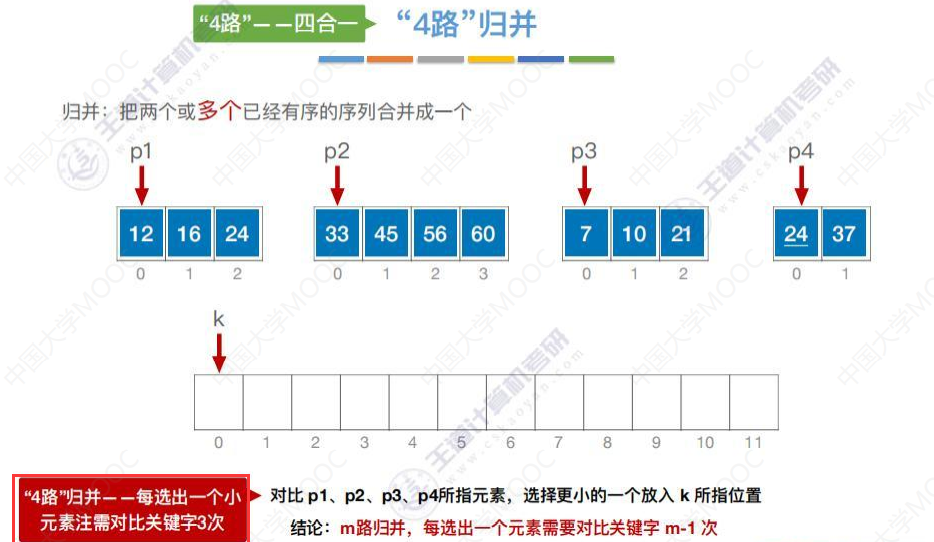
代码实现Merge函数
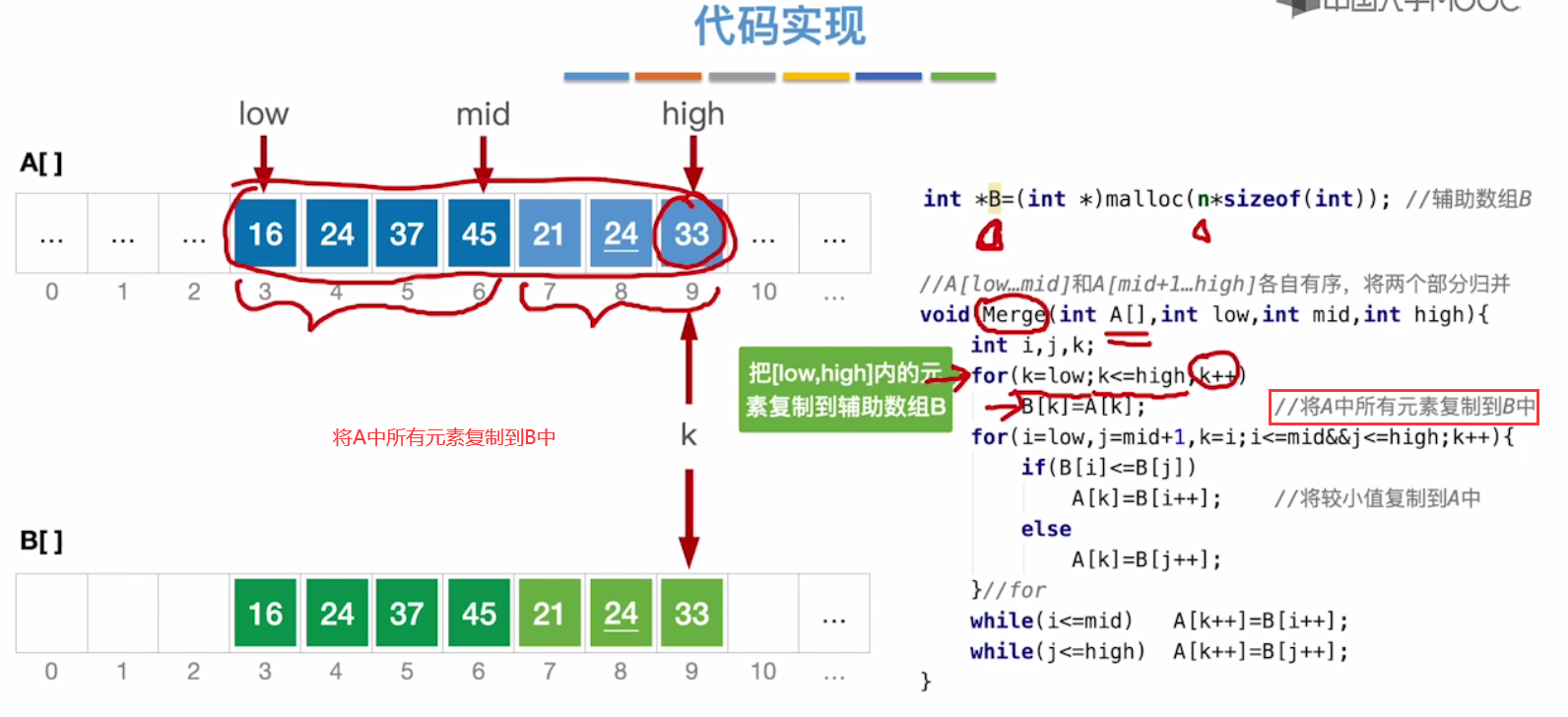
归并排序有稳定性
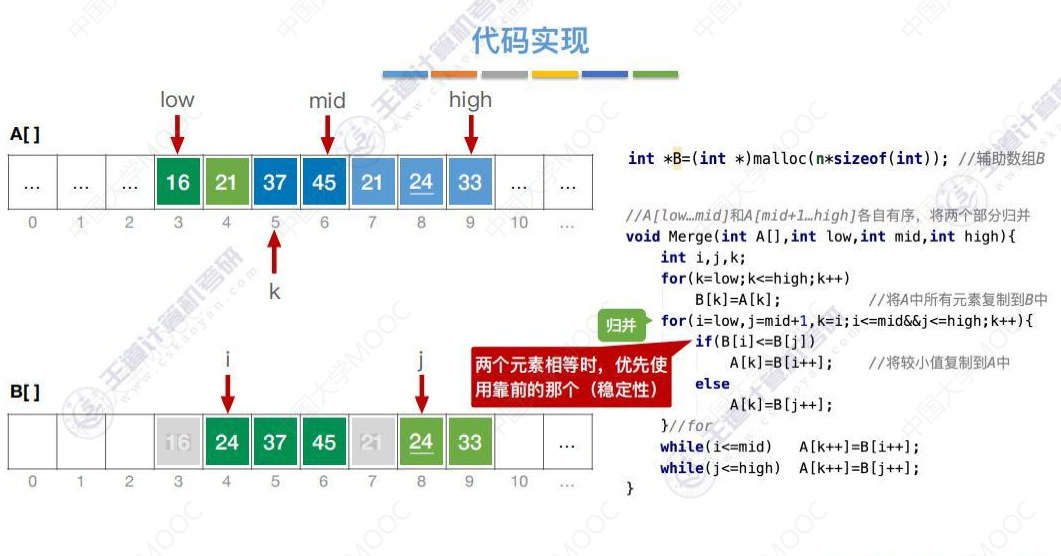
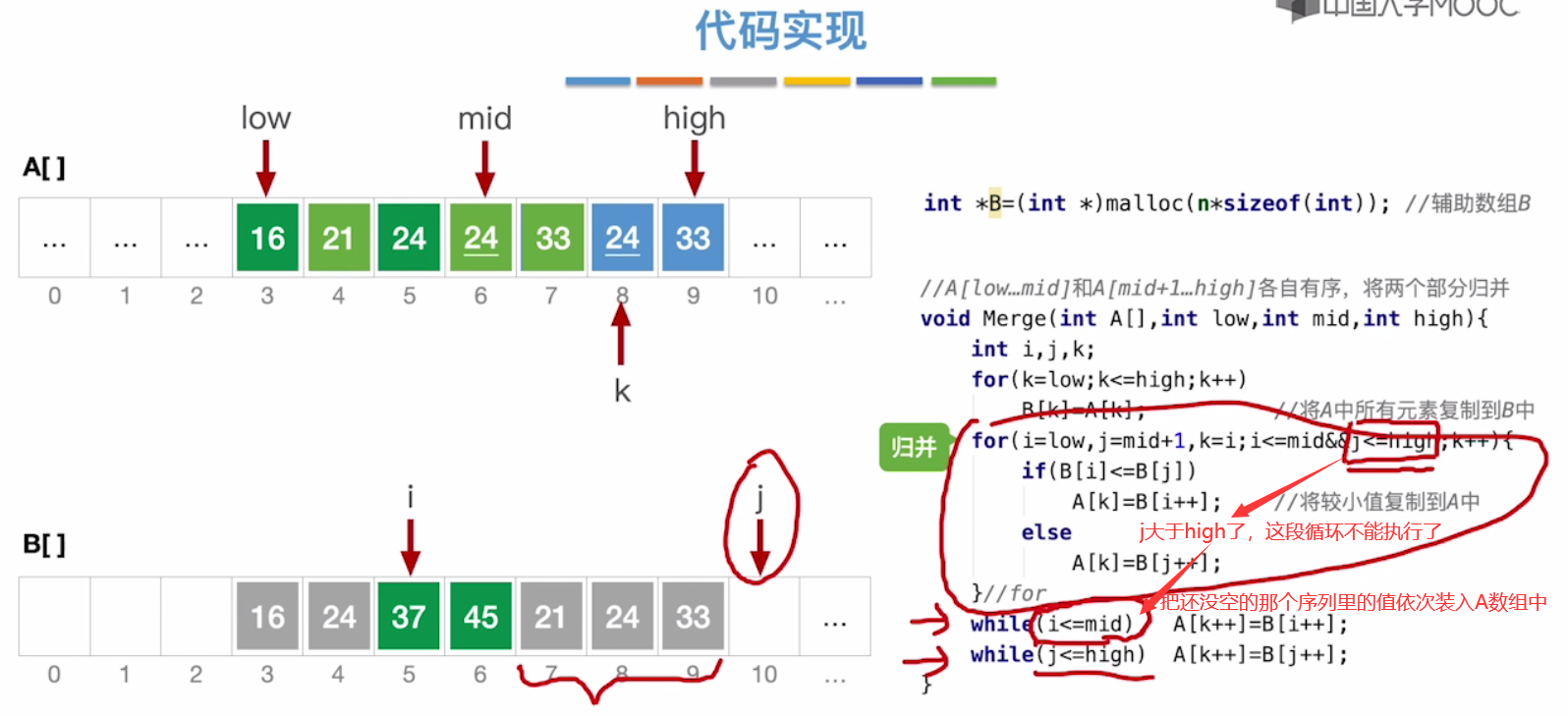
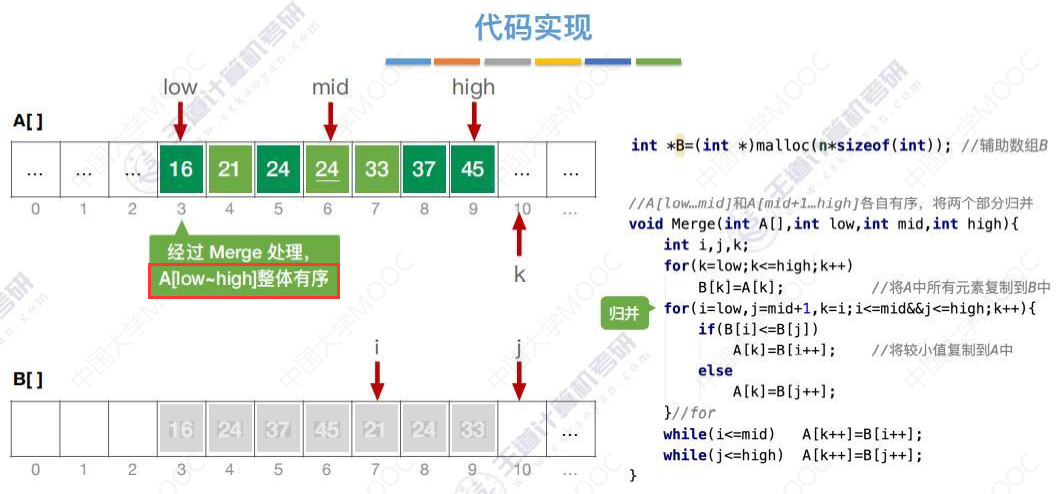
代码递归实现MergeSort
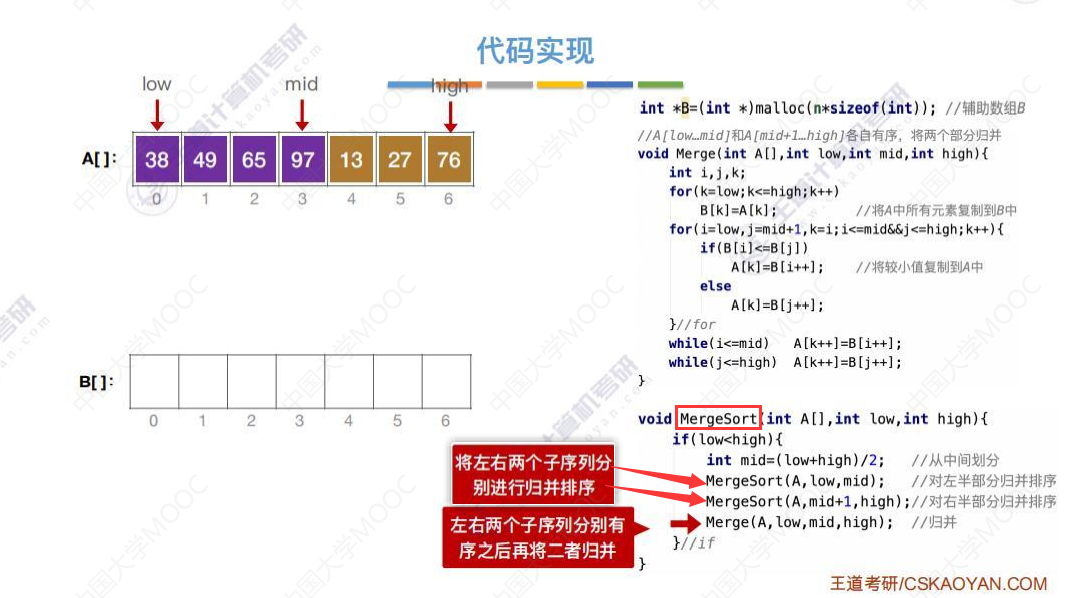
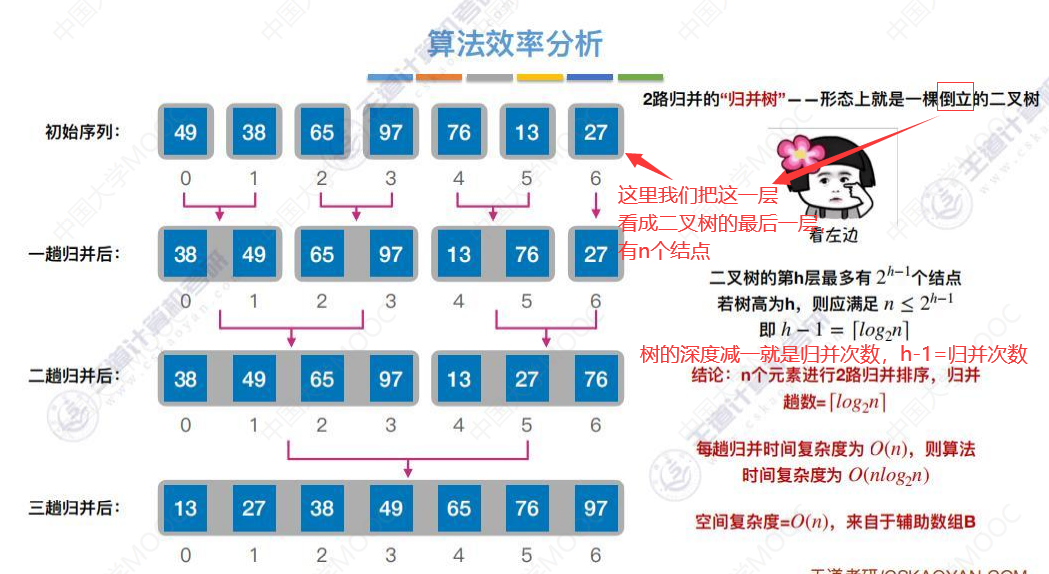
算法效率分析
第一次归并对比关键字次数3次,相当于n/2,是O(n)数量级。
第三次归并:每对比关键字一次,就能挑出一个当前还剩余的更小的元素。最多进行n-1次关键字的对比,就能完成一趟归并。
所以 不管是那一次的归并,都是O(n)的数量级的时间。
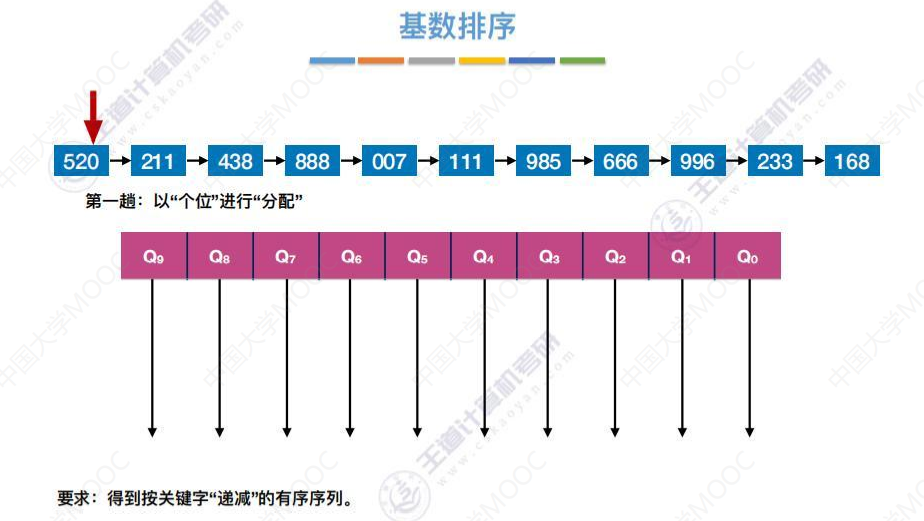
8.5-2 基数排序
基数排序示例
第一趟
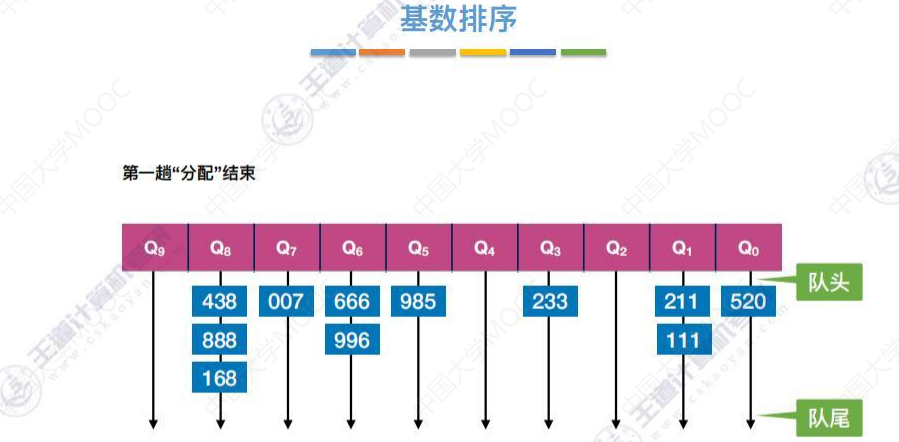
靠近队头的连在前面,靠近队尾的连在后面。
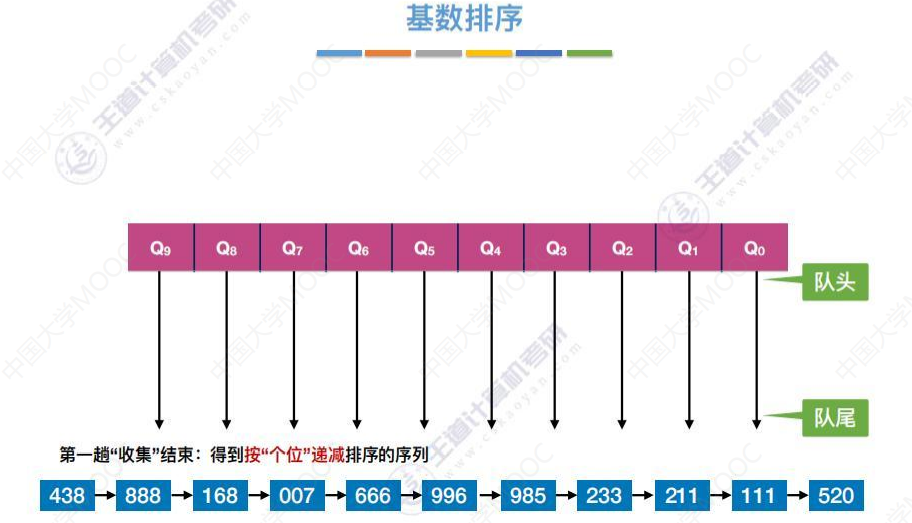
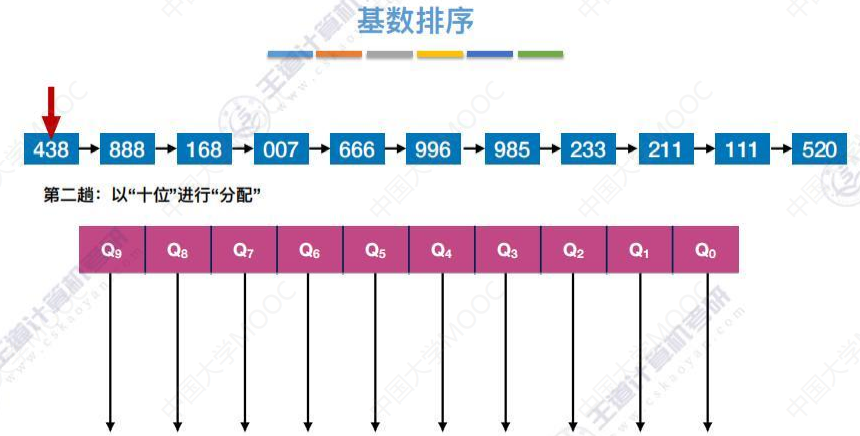
第二趟
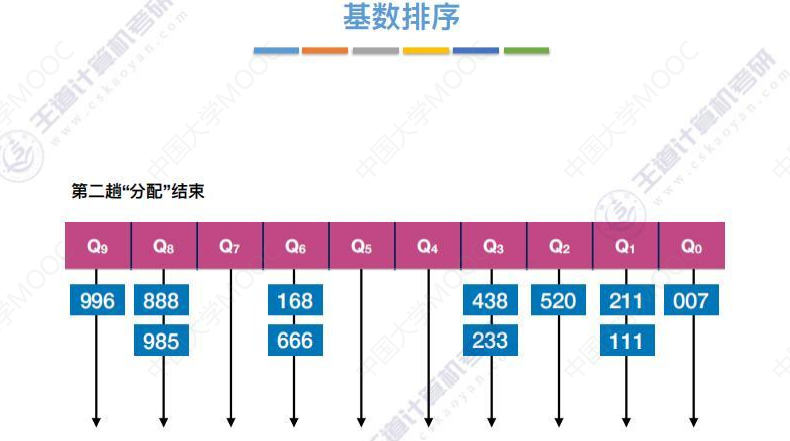
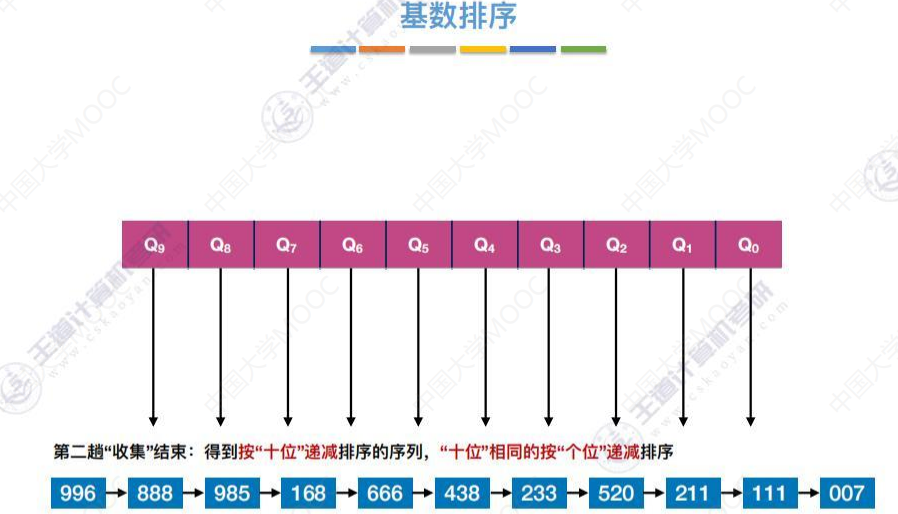
第三趟
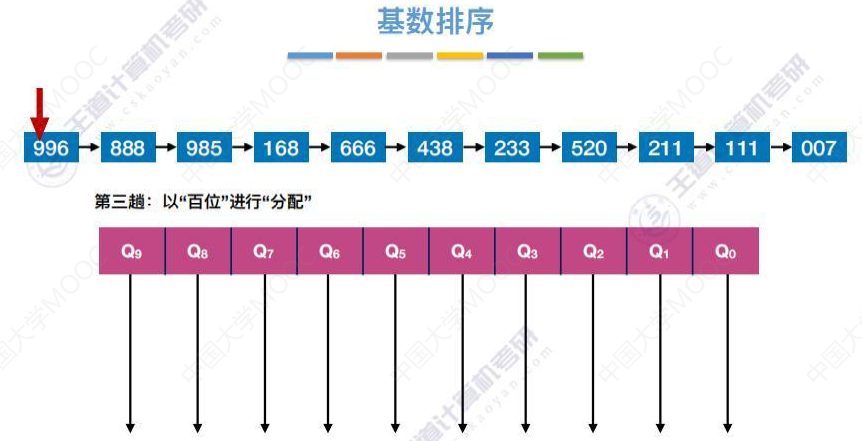
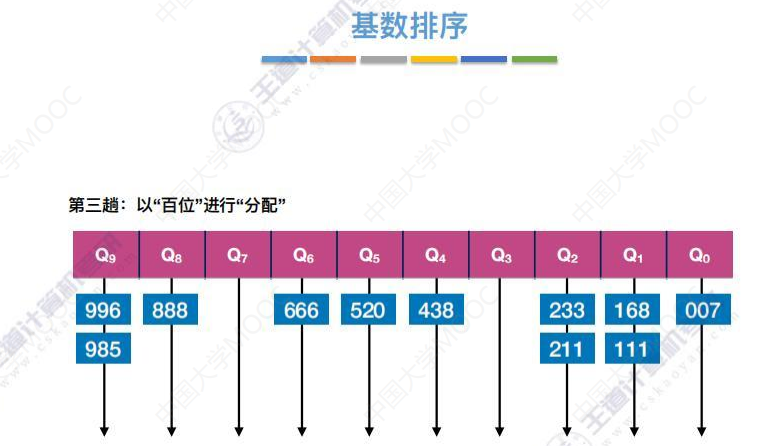
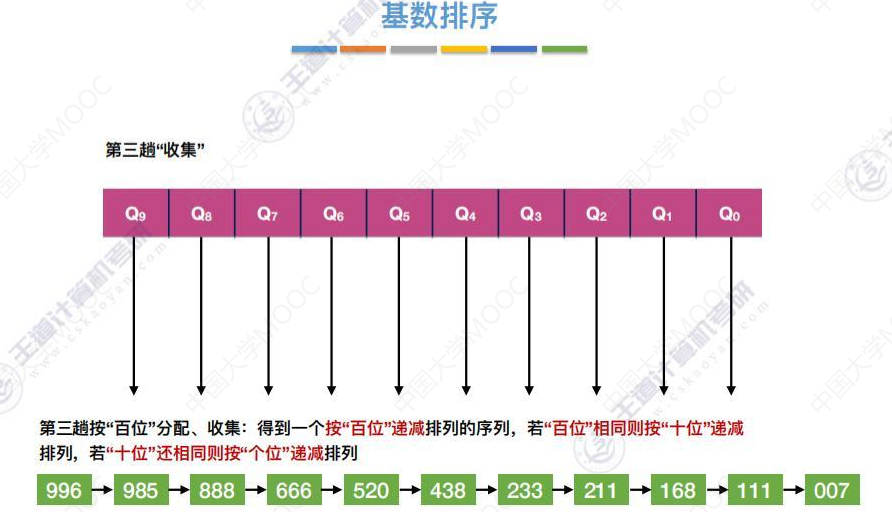
基数排序总体顺序
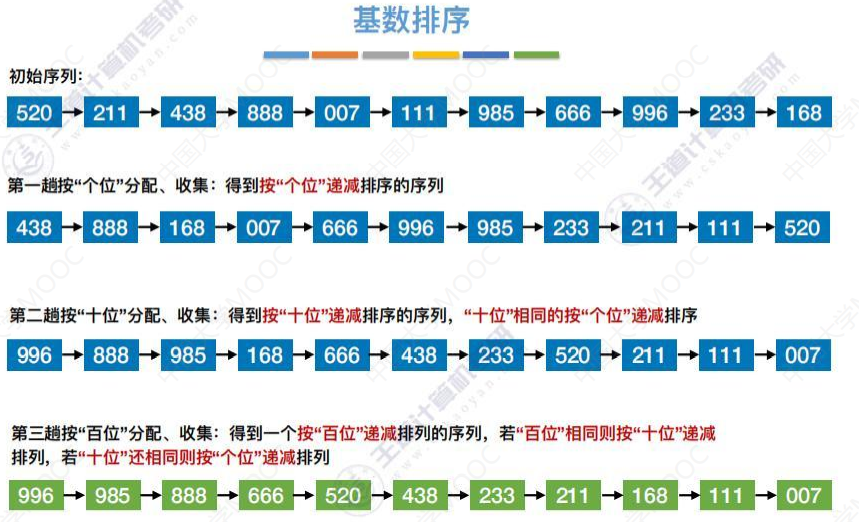
基数排序得到递减序列的过程
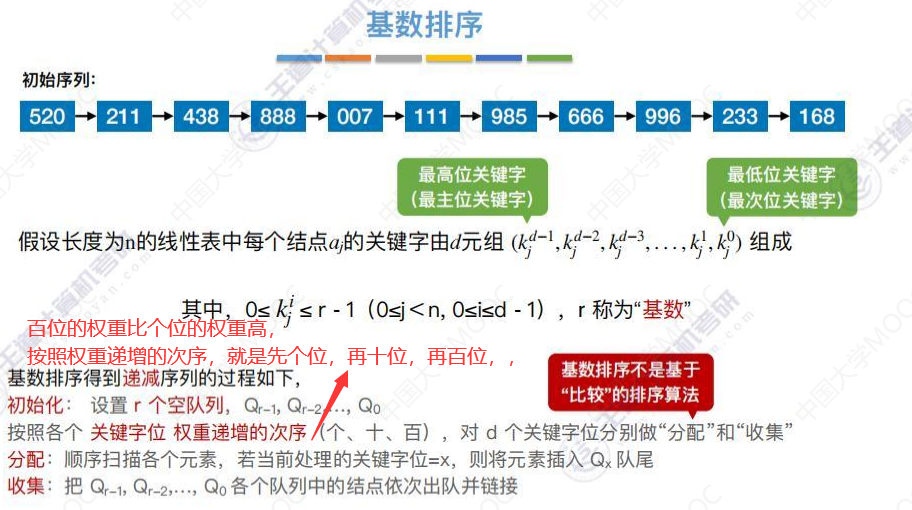
基数排序得到递增序列的过程
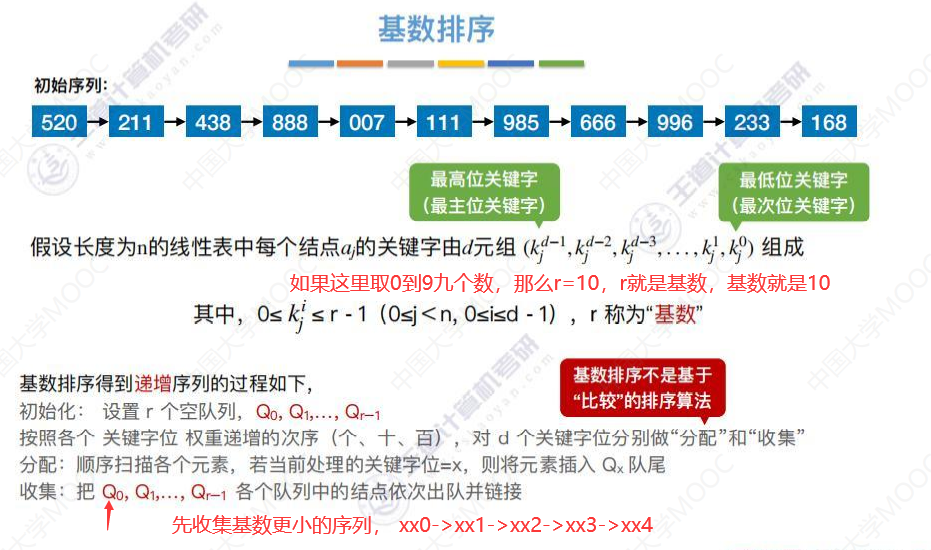
算法效率分析
每新增一个队列就是新增两个指针域的空间。
下图r就是10,代表0-9 10个辅助队列,
d就是关键字能被拆成几个部分。
每次分配其实就是从头到尾把链表元素扫一遍,有n个元素,扫一遍需要有O(n)的时间。
一次收集就是逐个的扫描这些队列,把这些队列上的元素都给拆下来,合成一条新链表。
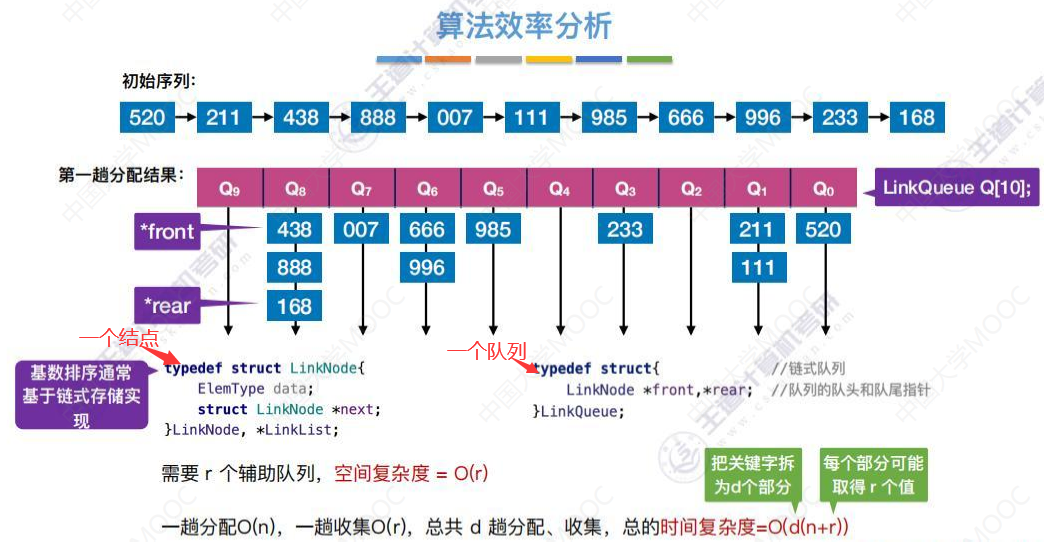
收集一个队列只需O(1)的时间,如下图, 后,这一队列的全部元素就串到下面的链表中了,只需要O(1)的时间。
后,这一队列的全部元素就串到下面的链表中了,只需要O(1)的时间。
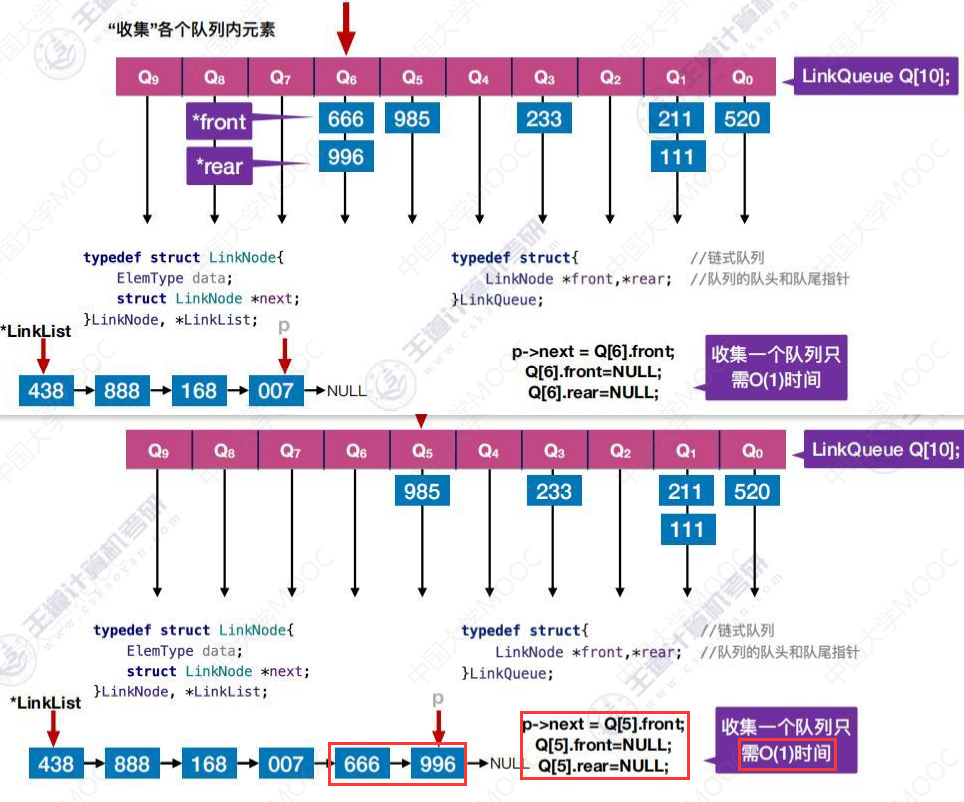
稳定性分析
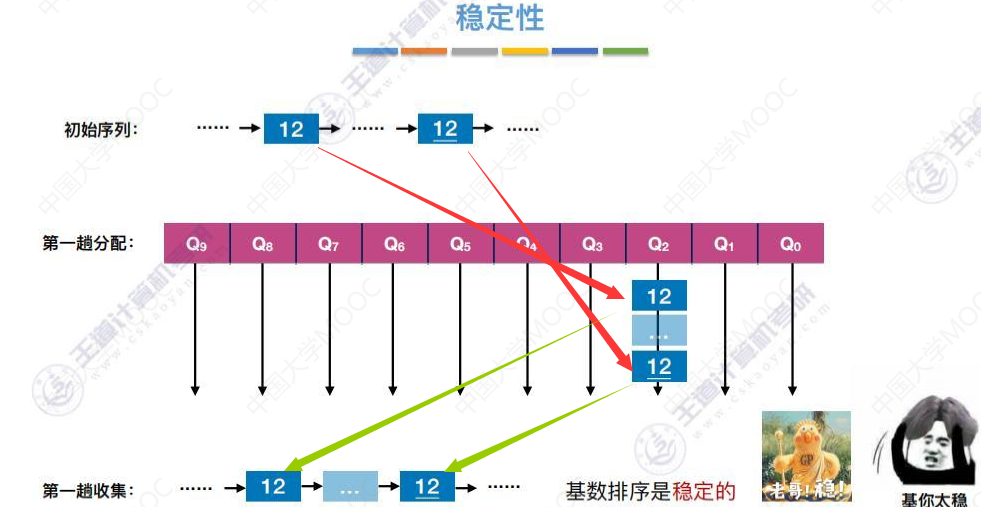
8.7-1 外部排序
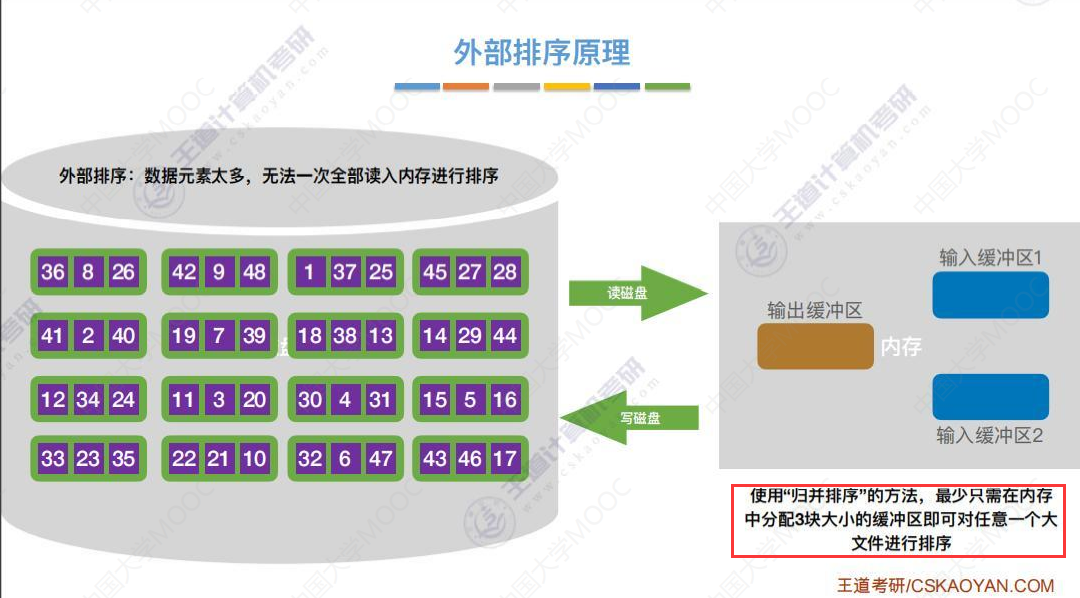
外部排序使用的是归并排序
磁盘的读/写以“块"为单位数据读入内存后才能被修改修改完了还要写回磁盘。
“归并排序”要求各个子序列有序,每次读入两个块的内容,进行内部排序后写回磁盘。所以先进行一次内部排序将各个初始归并块有序,后面才能进行归并排序。
若要进行k路归并排序,则需要在内存中分配k个输入缓冲区和1个输出缓冲区。
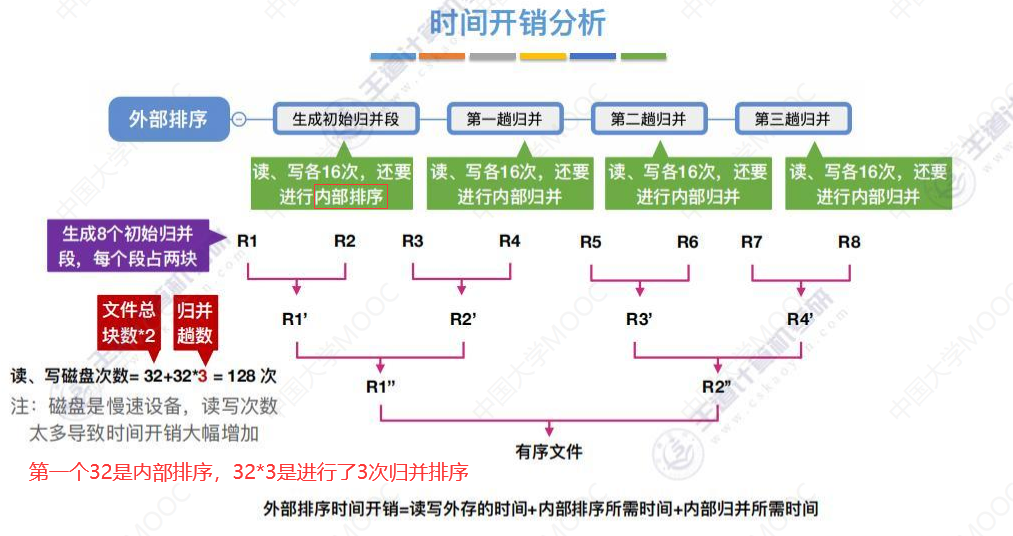
时间开销分析
读写次数是主要消耗时间的步骤。
“归并排序”要求各个子序列有序,所以先进行一次内部排序使初始归并块有序,然后才能进行归并排序。
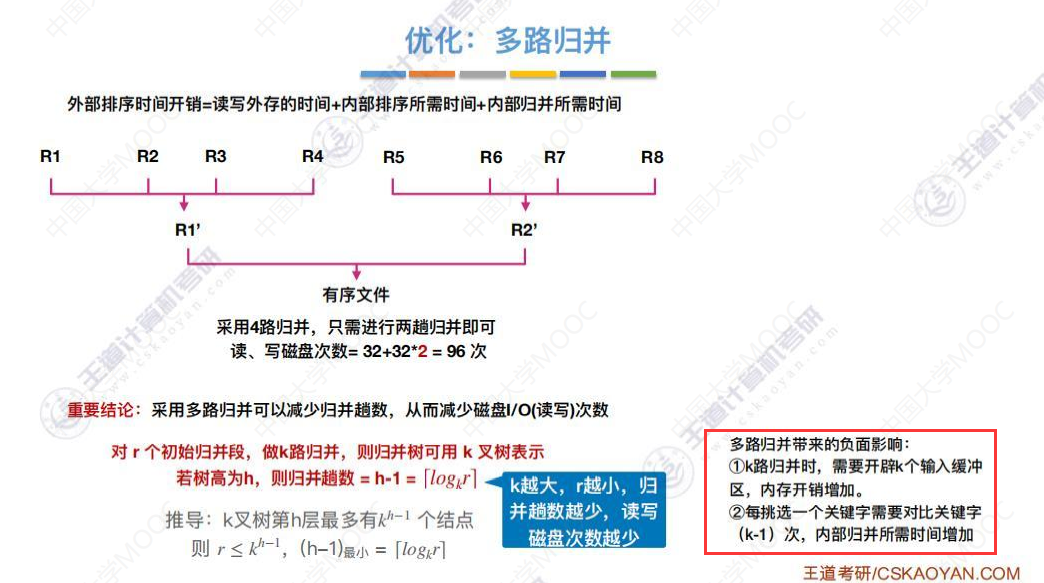
两个优化方法
优化1:多路归并
若要进行k路归并排序,则需要在内存中分配k个输入缓冲区和1个输出缓冲区。
下图是4个输入缓冲区和1个输出缓冲区

优化2:减少初始归并段数量
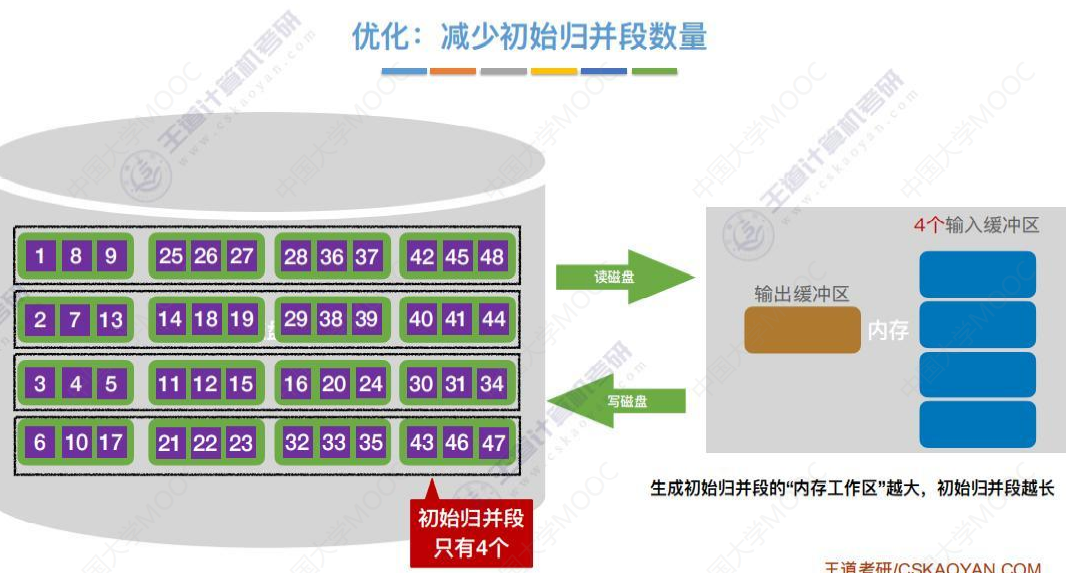
每个初始归并段越长,初始归并段的个数r就越少,归并趟数就越少,读写磁盘的次数就越少。
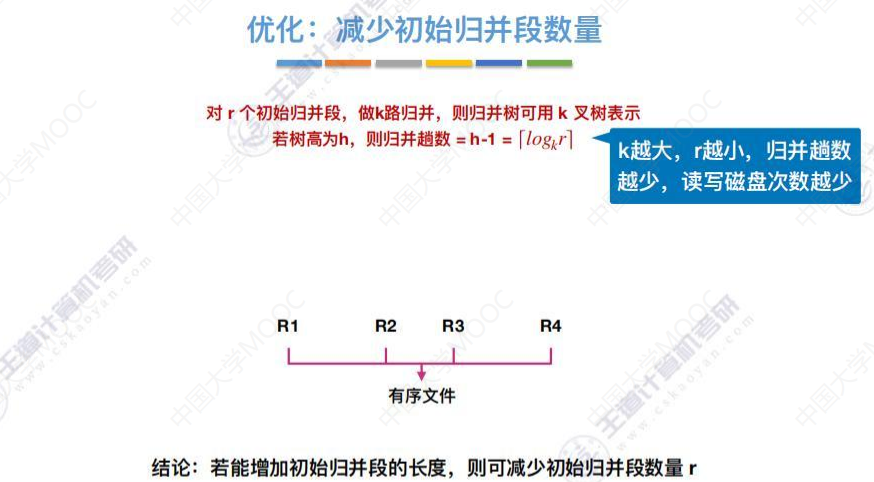
总结
若要进行k路归并排序,则需要在内存中分配k个输入缓冲区和1个输出缓冲区
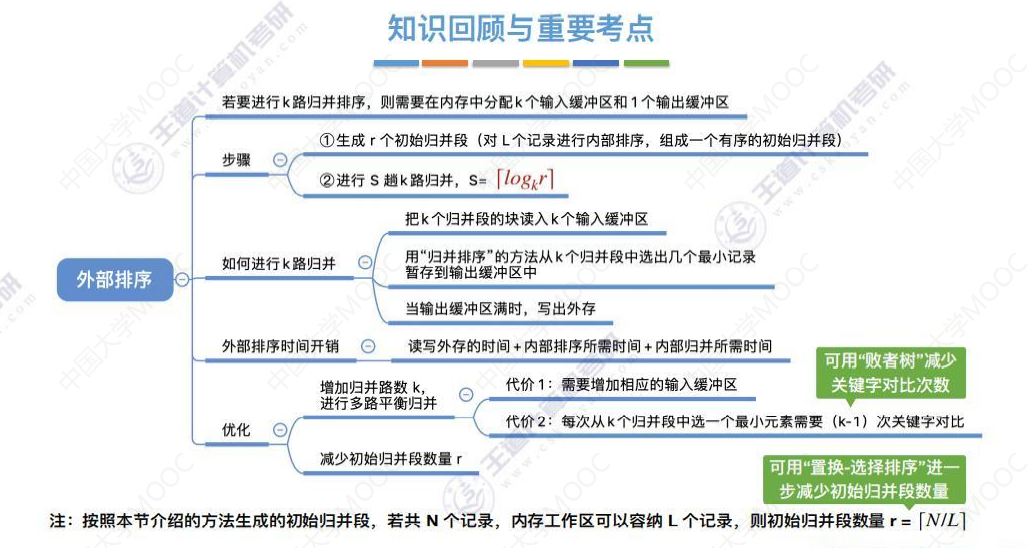
多路平衡归并
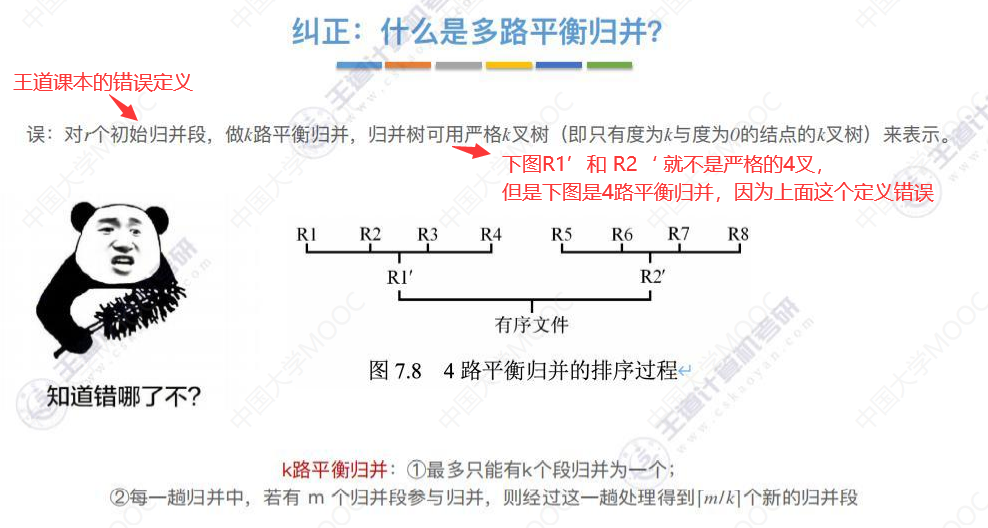
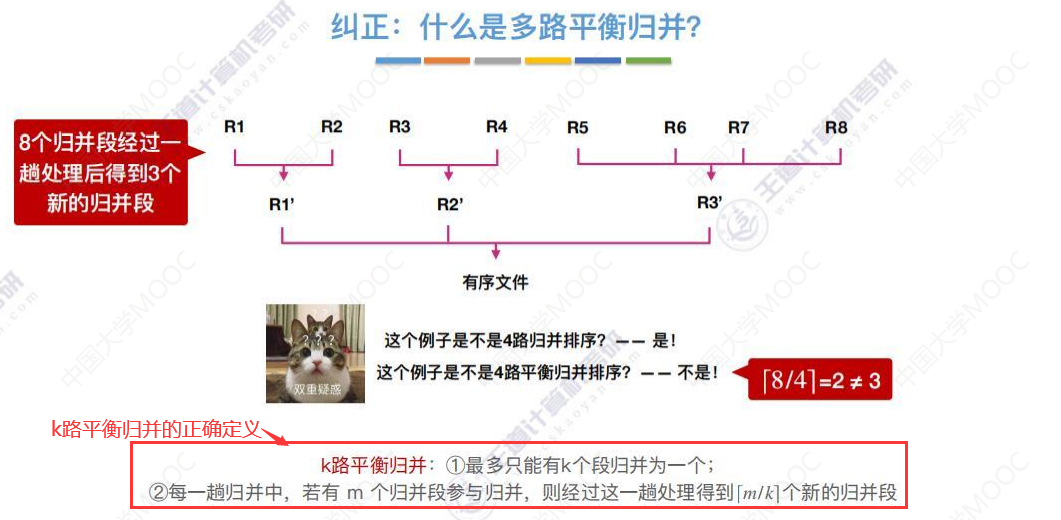
8.7-2 败者树
问题引入
8路平衡归并,从八个归并段中选出一个最小元素需要对比关键字7次,每次都要对比很多元素,造成时间的大量消耗。

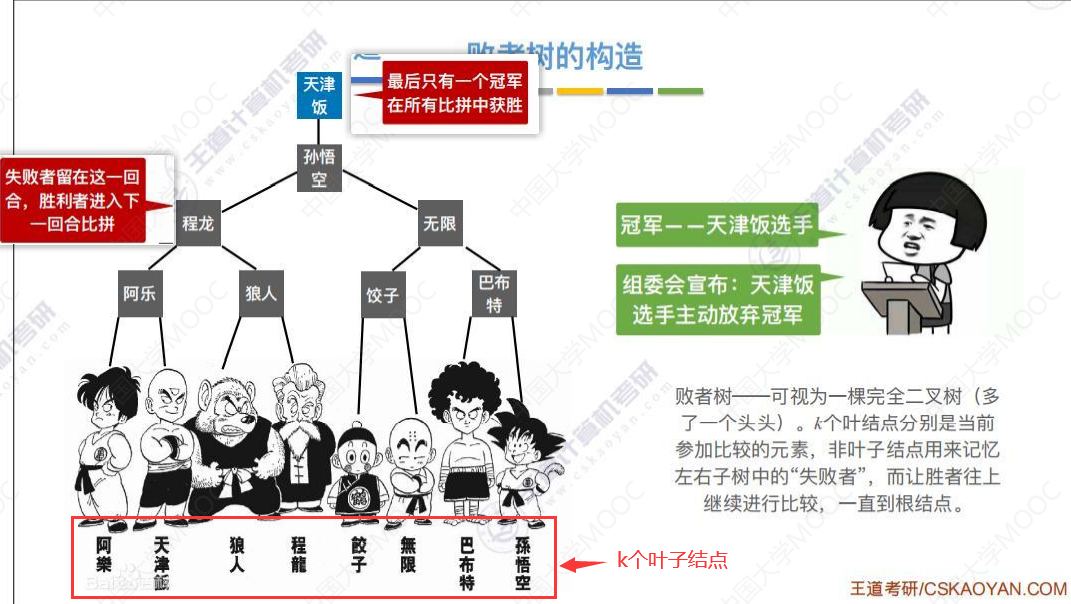
败者树的构建
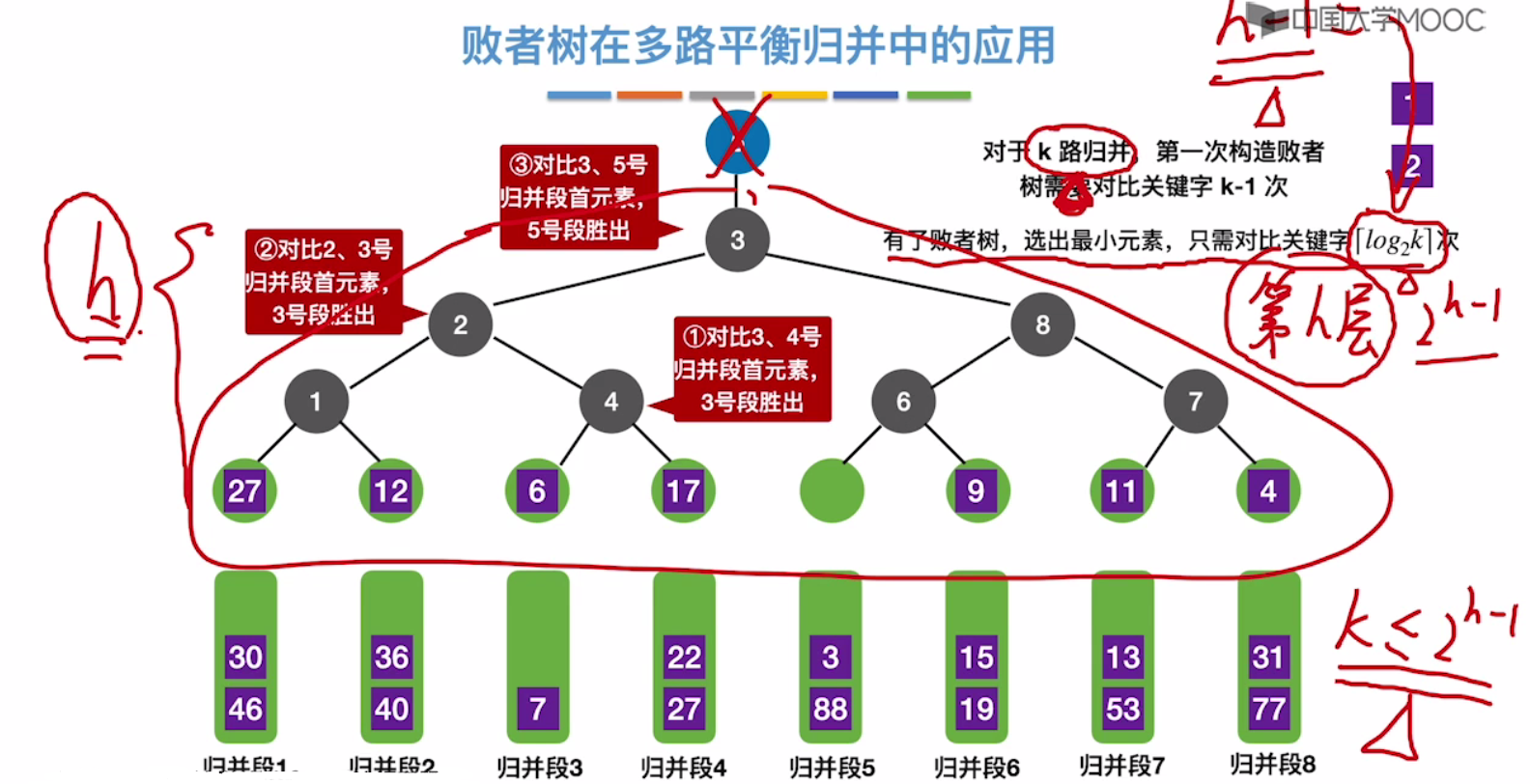
败者树在多路平衡归并中的应用
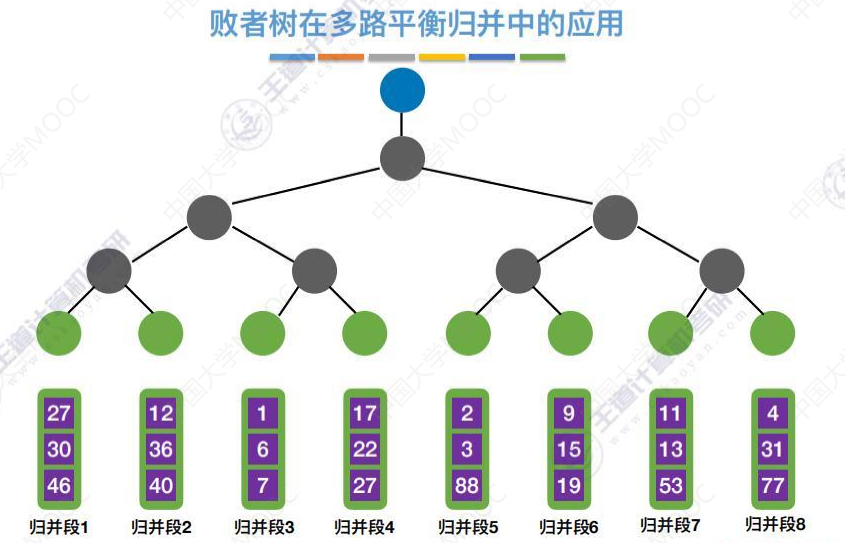
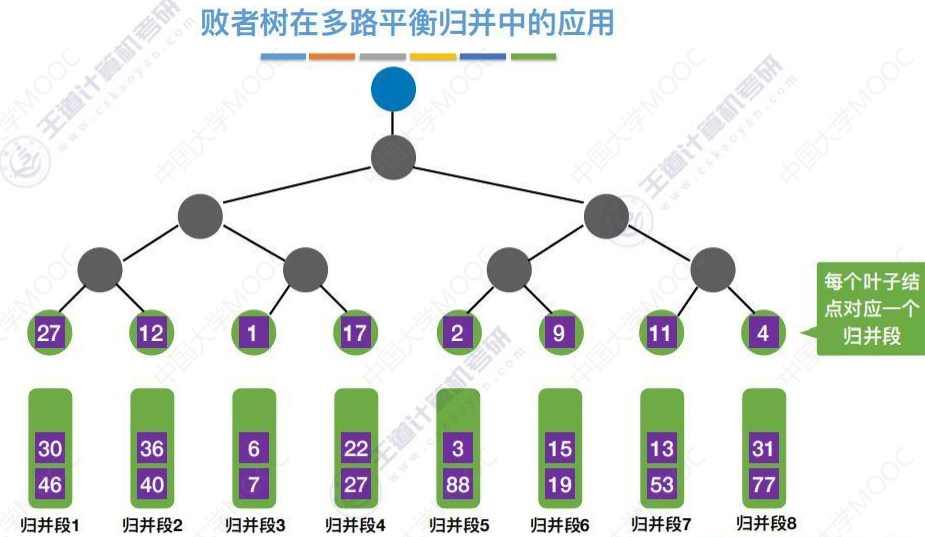
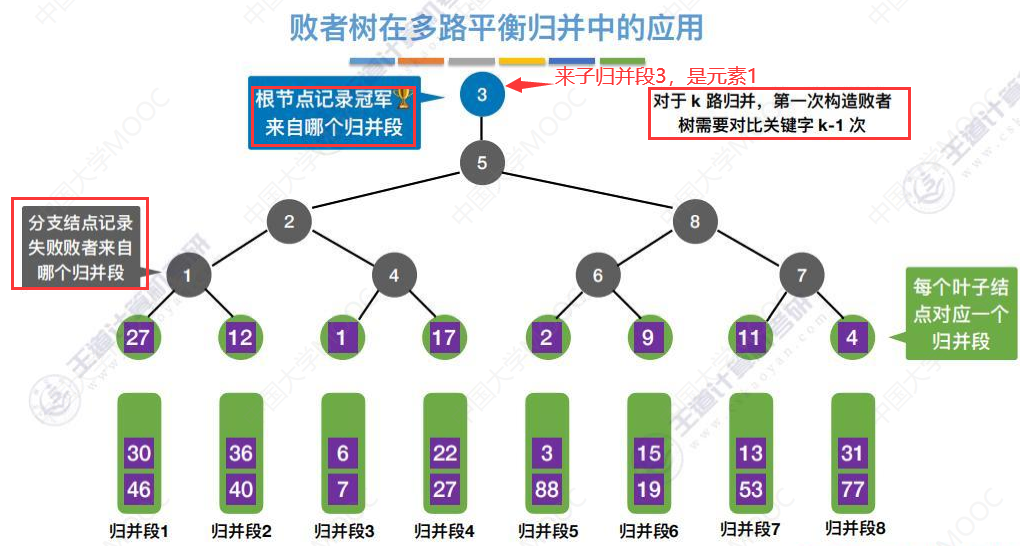
将归并段3的这个最小的元素1 弹出,进入归并序列。
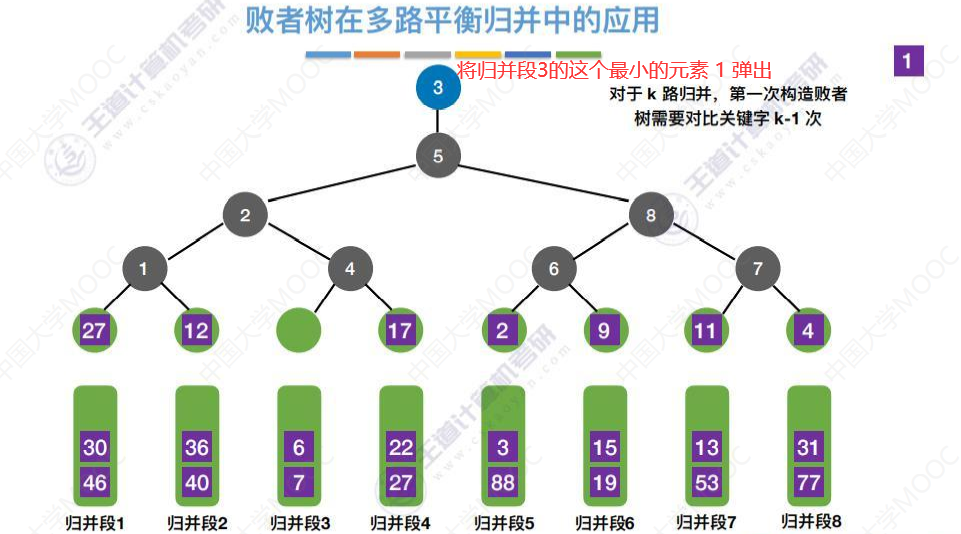
从归并段3弹出一个元素填补空位置。
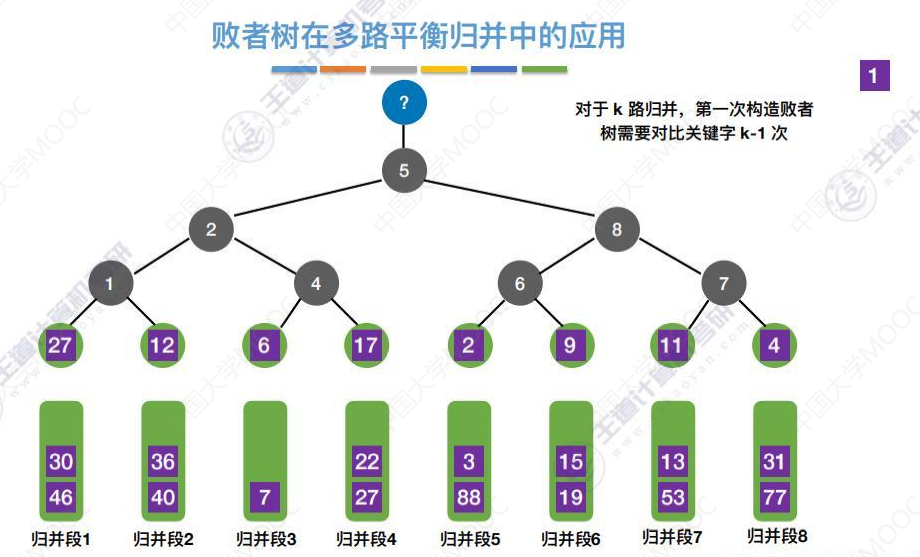
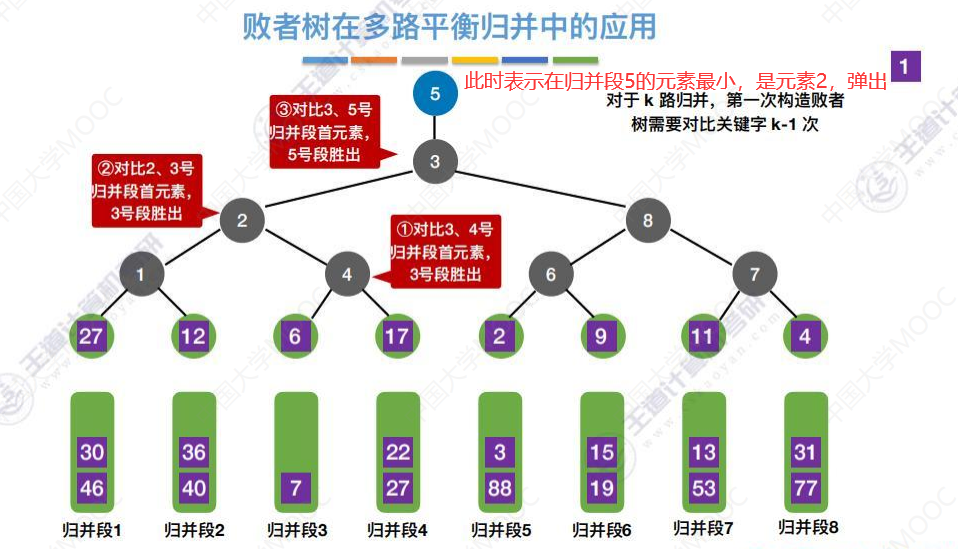
有了败者树,选出最小元素,只需对比关键字[log2(k)]次。
k路归并,就是叶子节点是k个。
下图树高4,要对比关键字3次,那么树高h,要对比关键字h-1次。
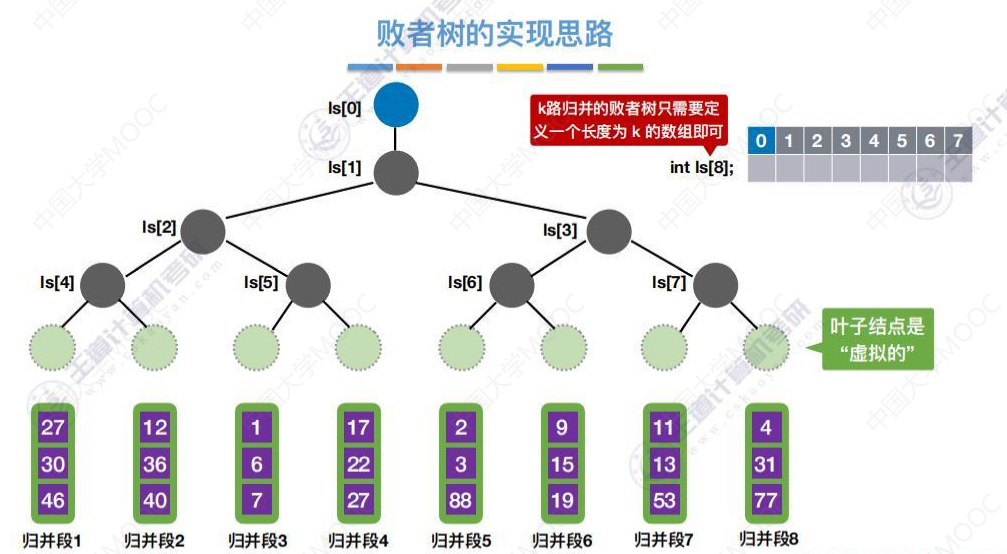
败者树的思路实现
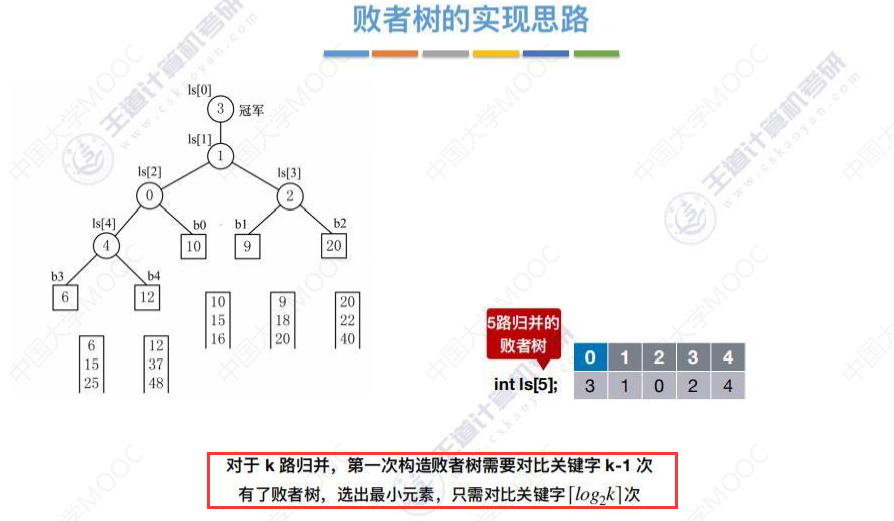
对于k路归并,第一次构造败者树需要对比关键字k-1次,有了败者树,除了第一次构造败者树需要对比关键字k-1次外,其他的时候选出最小元素,只需对比关键字[log2(k)]次。
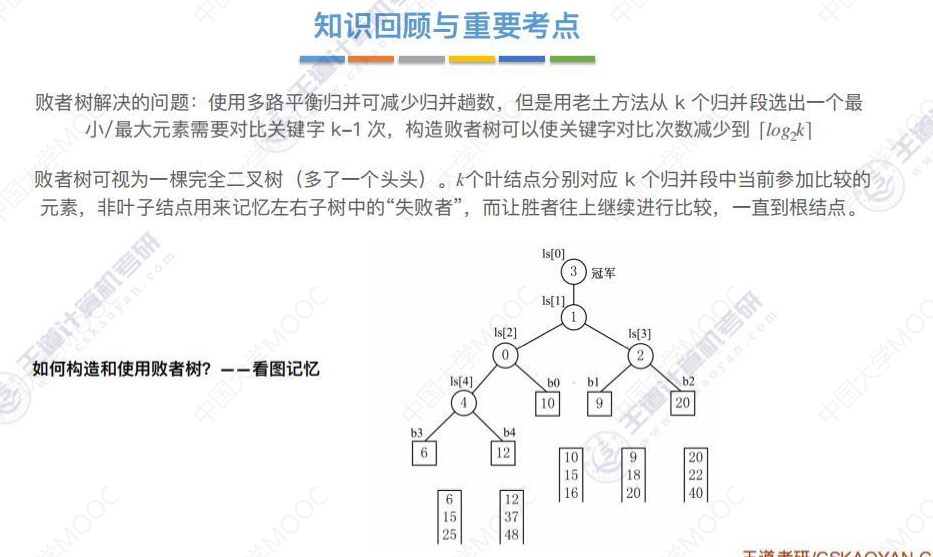
8.7-3 置换_选择排序
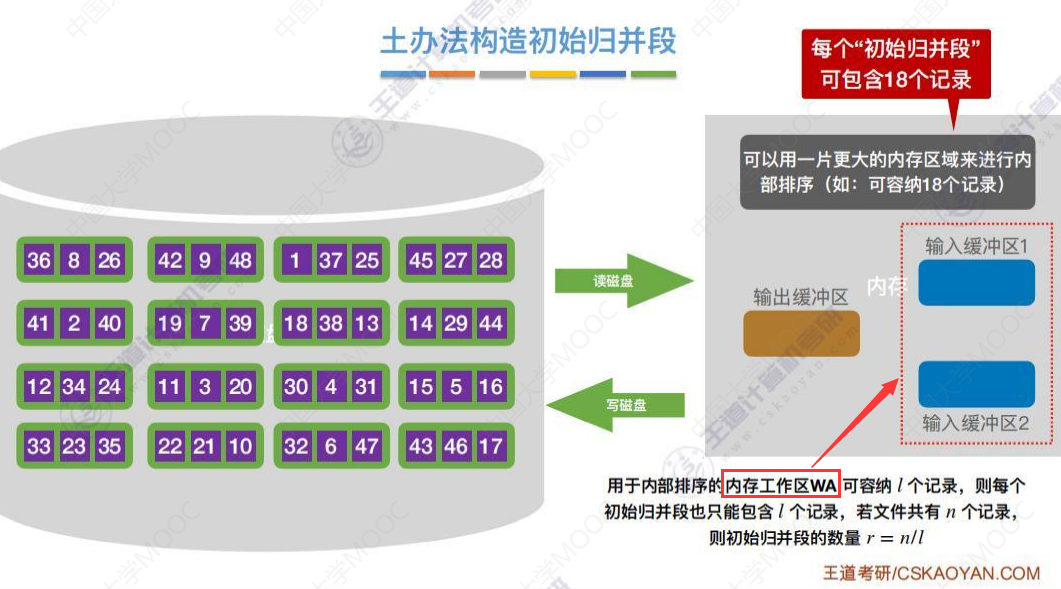
传统方法的初始归并段数量计算方法如下,可用“置换-选择排序”进步减少初始归并段数量

用于内部排序的内存工作区WA可容纳 l 个记录,则每个初始归并段也只能包含 l 个记录,若文件共有n个记录,则初始归并段的数量 r = n / l
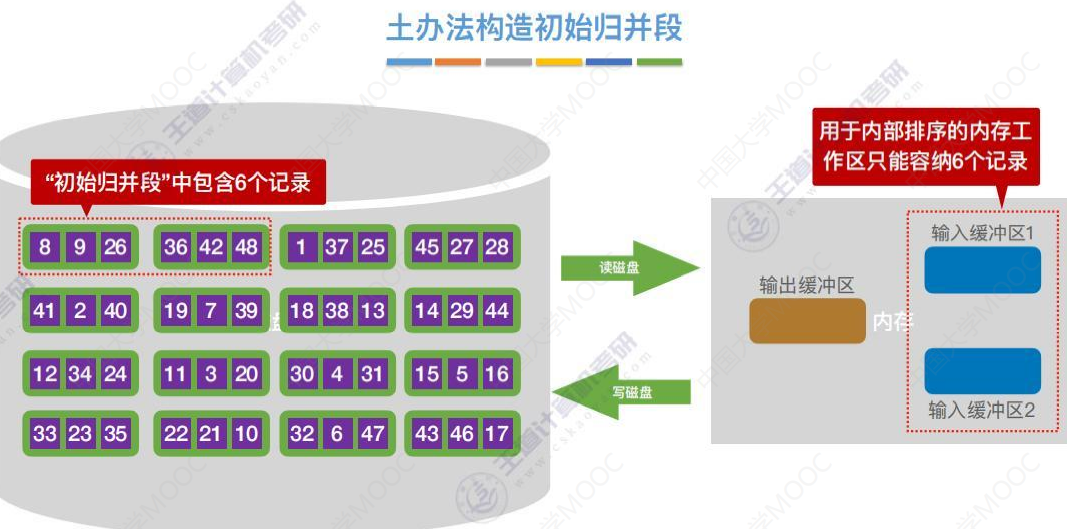
用于内部排序的内存工作区WA可容纳 6 个记录,则每个初始归并段也只能包含 6 个记录。
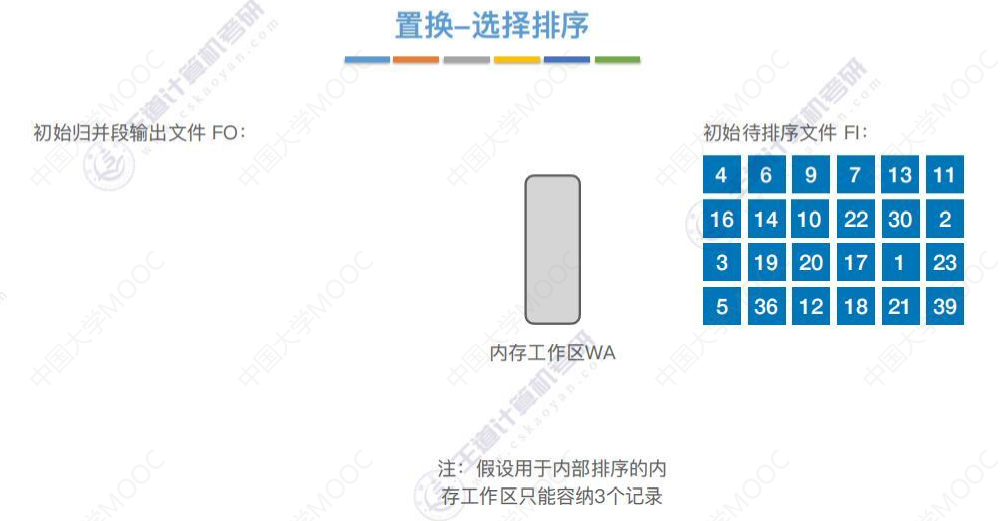
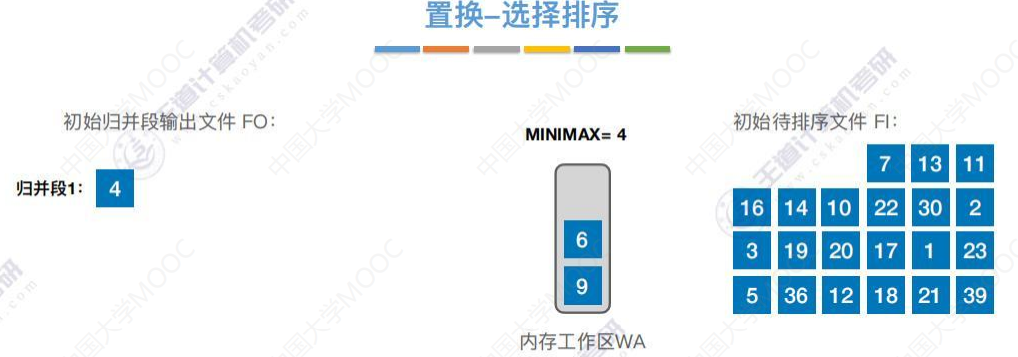
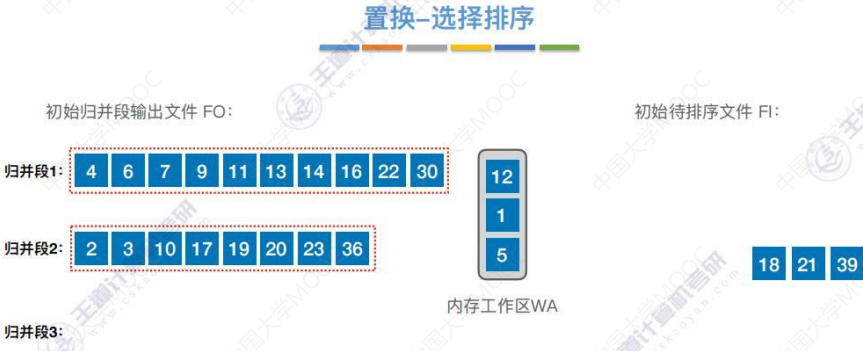
可用“置换-选择排序”进步减少初始归并段数量(示例)
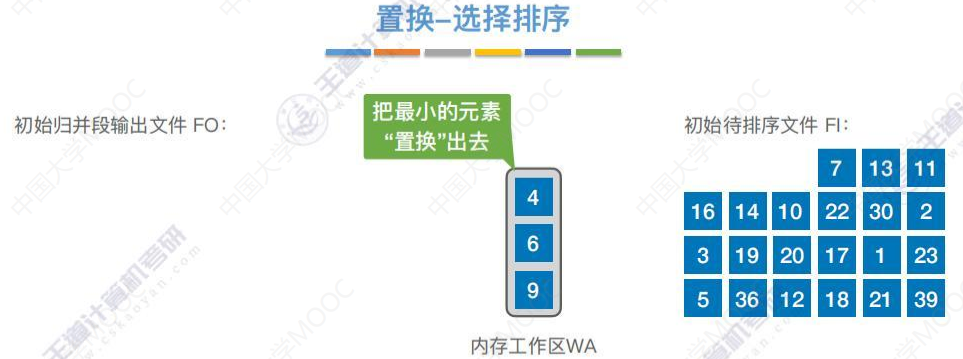
生成归并段的过程

生成归并段1
初始待排序文件FI在磁盘中,
初始待排序文件FO在磁盘中,
内存工作区WA在内存中。
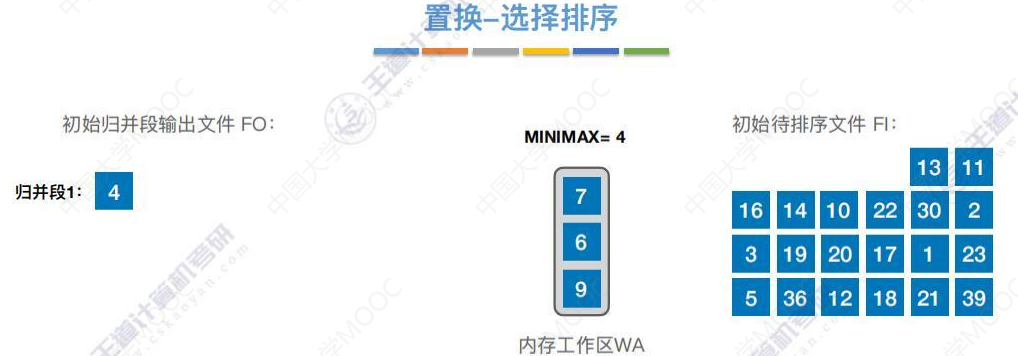
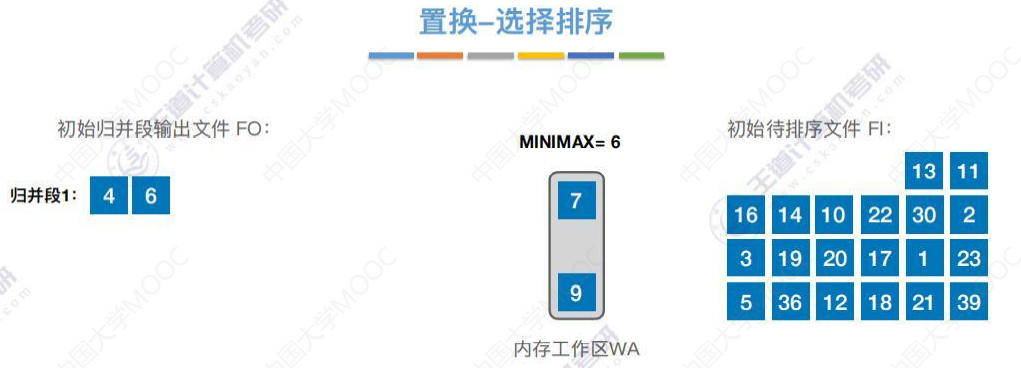


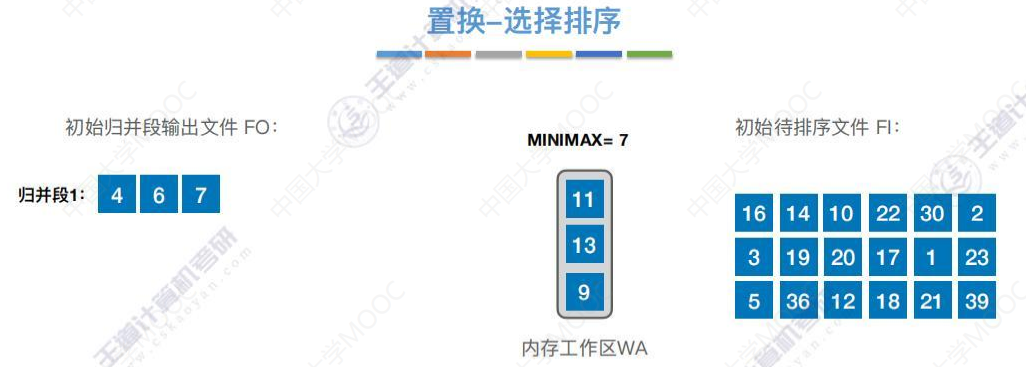




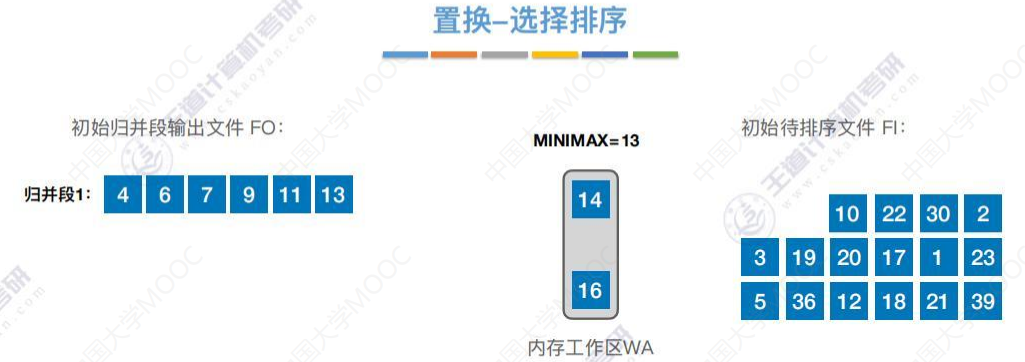












生成归并段2
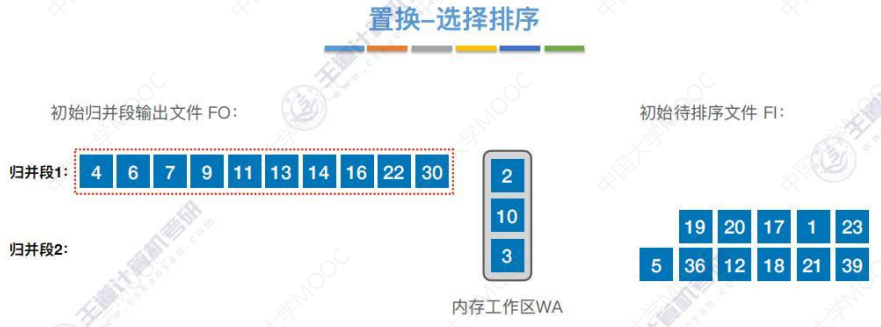
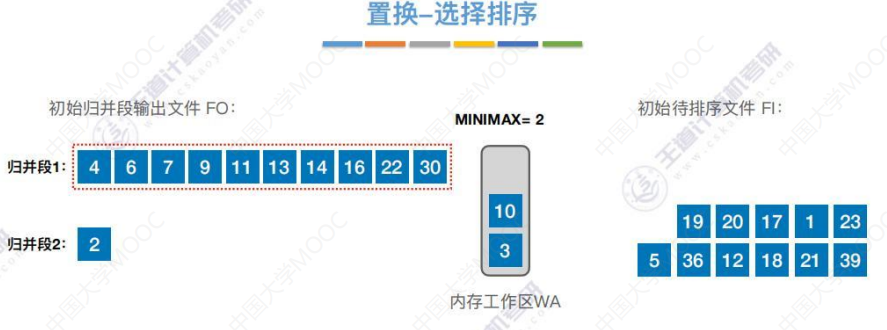
循环往复,
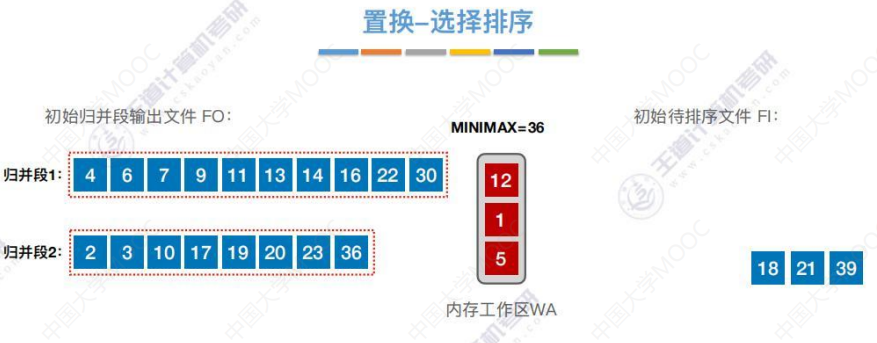
生成归并段3
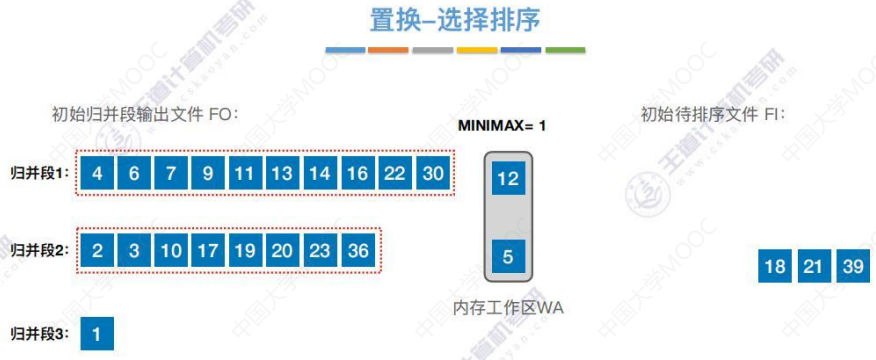
循环往复,
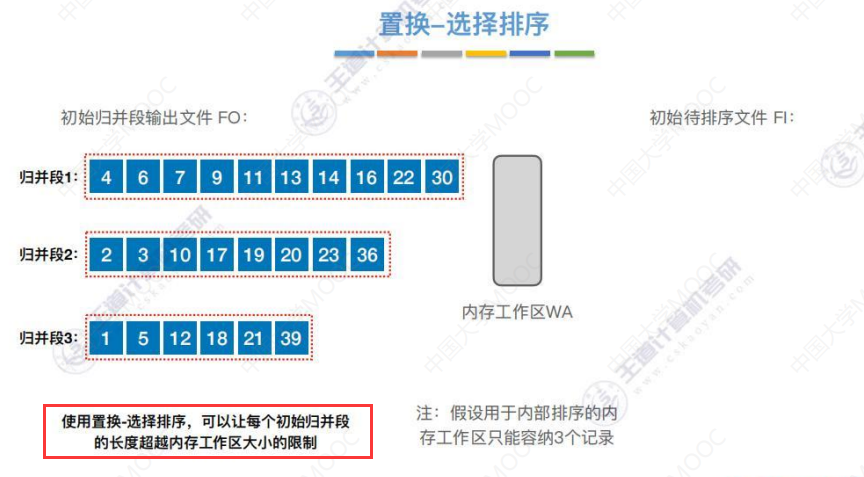
算法结束。
8.7-4 最佳归并树
归并树的性质
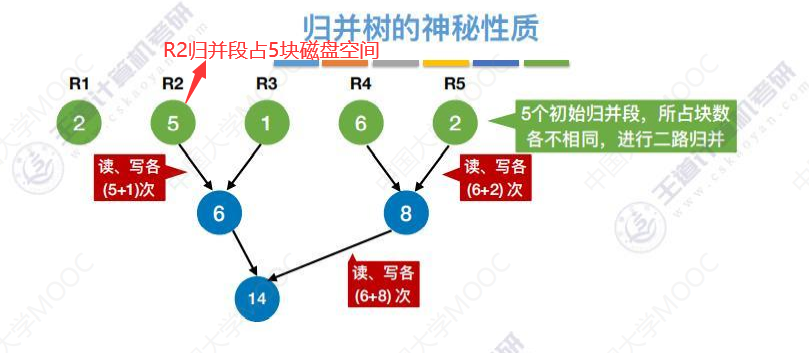
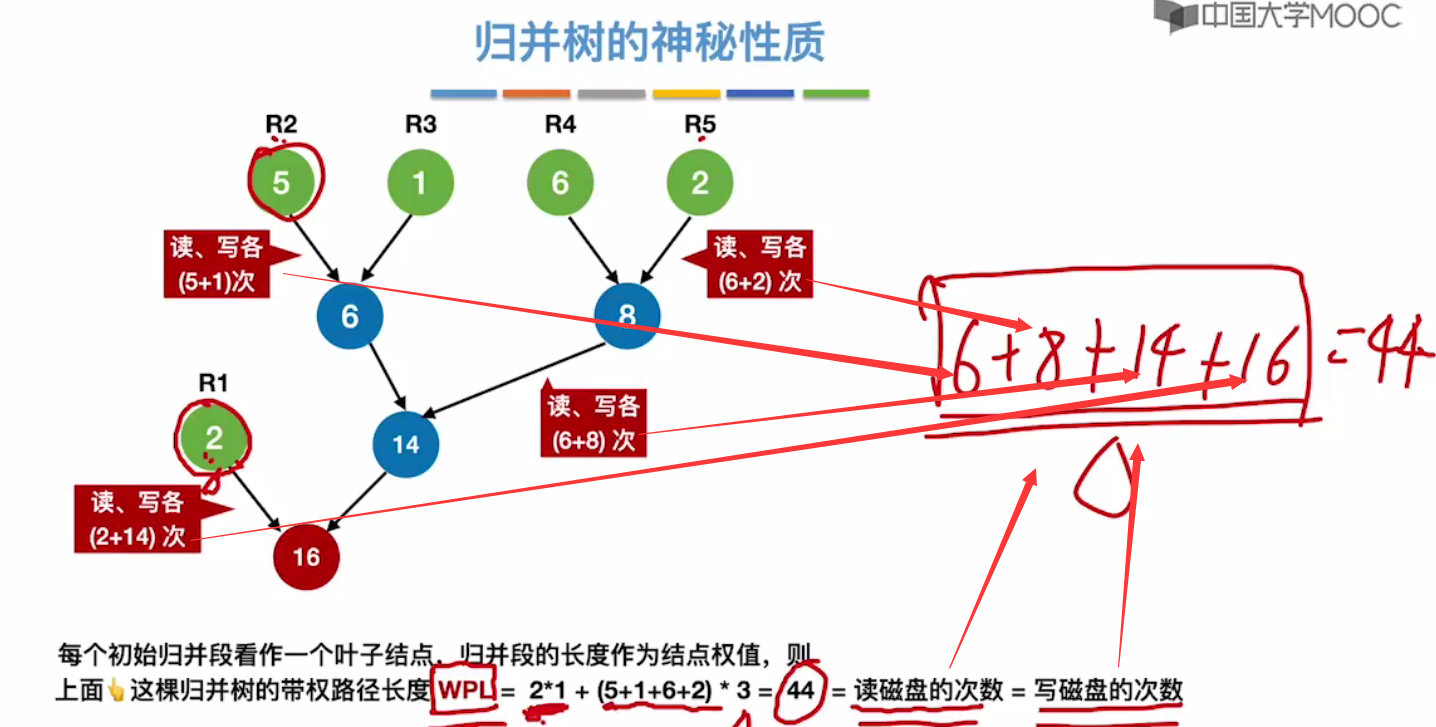
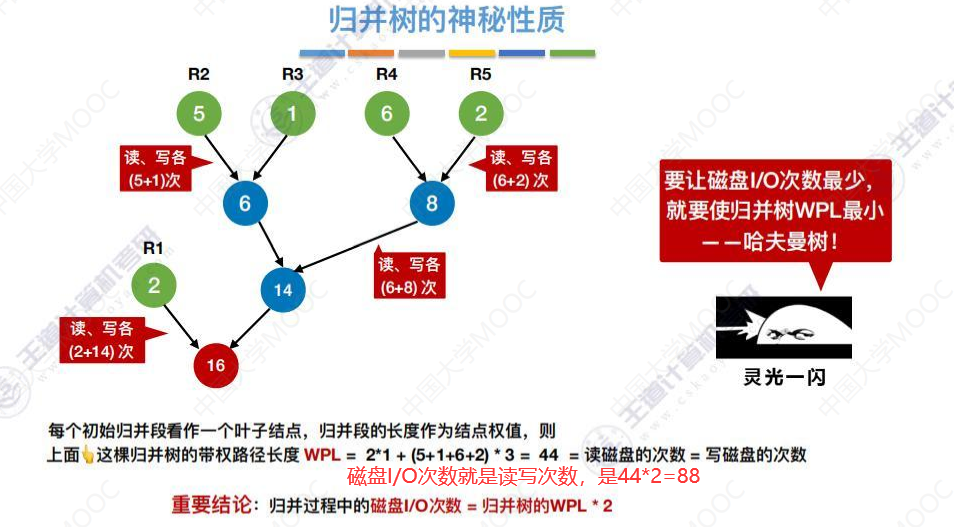
构建哈夫曼树,首先要挑选权值最小的两个结点使之成为兄弟。
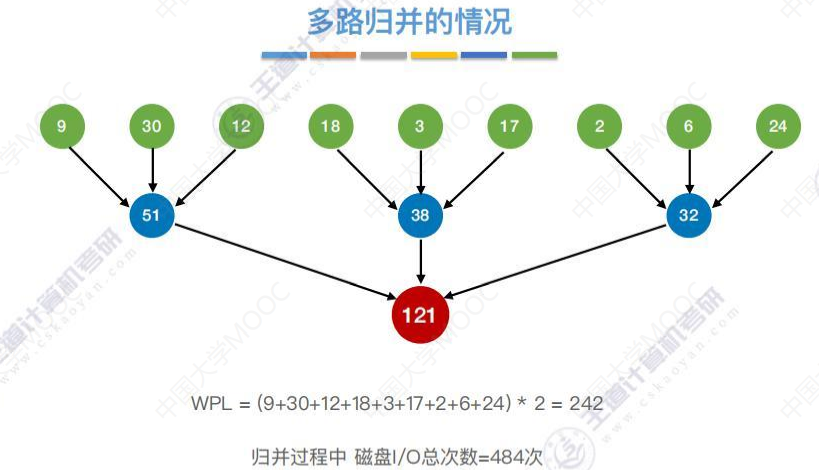
多路归并的情况
第一个归并,得到蓝色的数字,读或写的次数为51+38+32=121,
第二次归并,得到红色的数字,这次读或写的次数121,
两次一共读或写的次数为242。
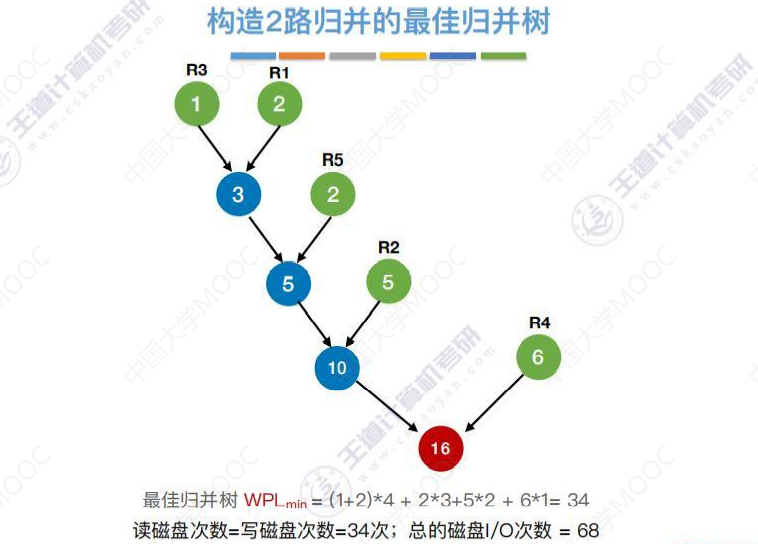
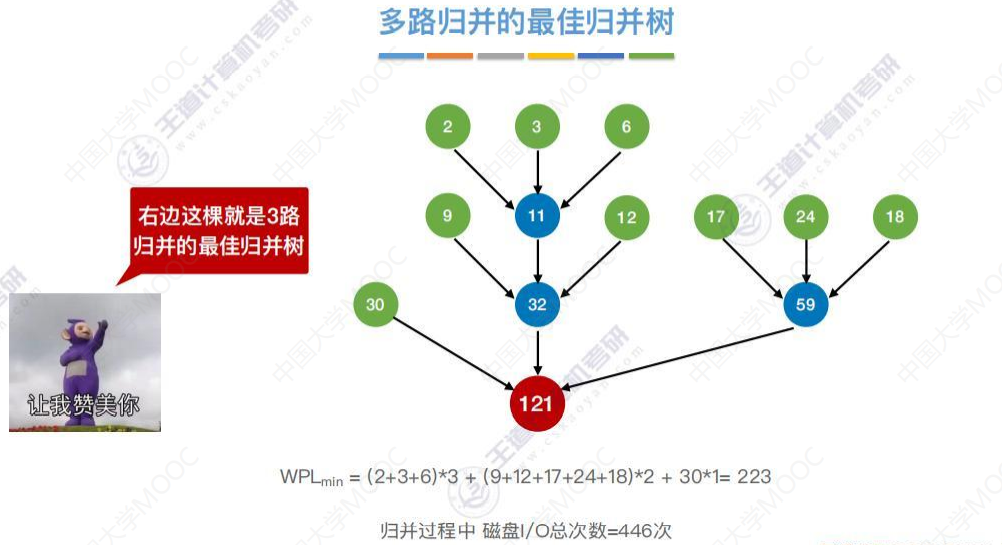
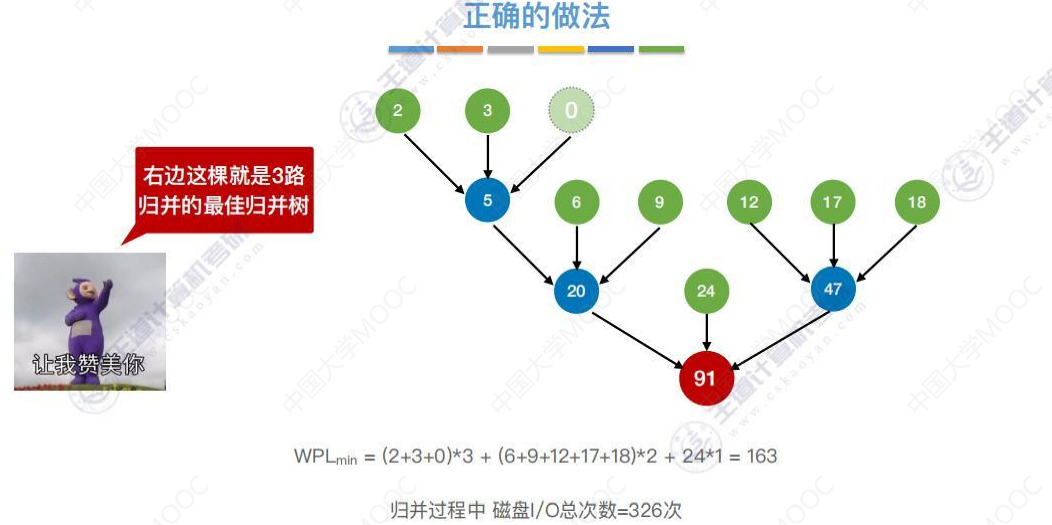
多路归并的最佳排序树

每次都选择3个最小的进行归并。
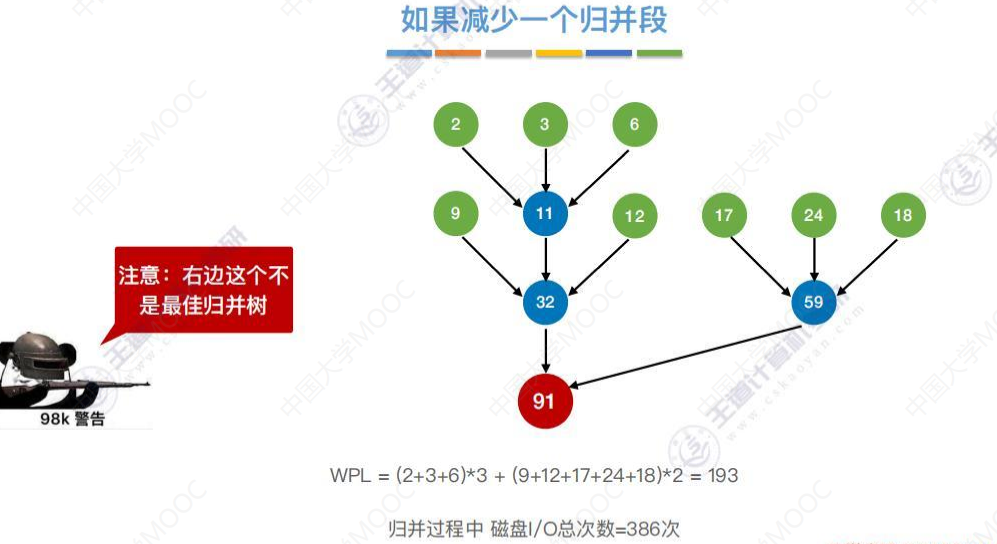
不是多路归并的最佳排序树

下图注意:k叉归并的最佳归并树一定是严格k叉树,即树中只有度为k、度为0的结点

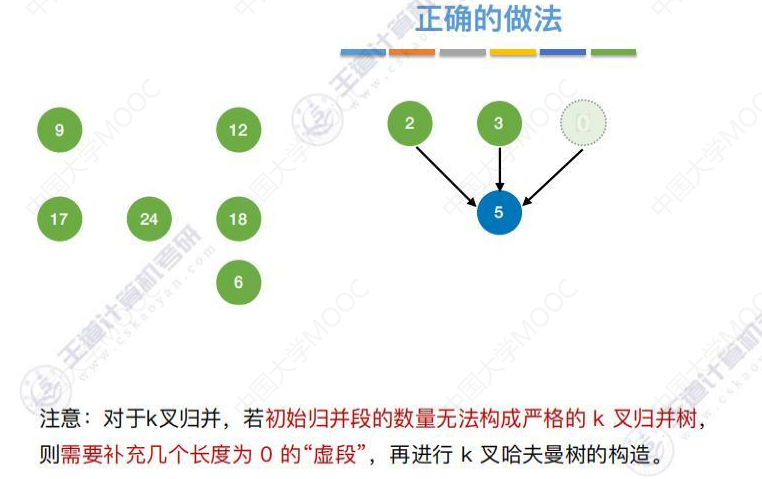
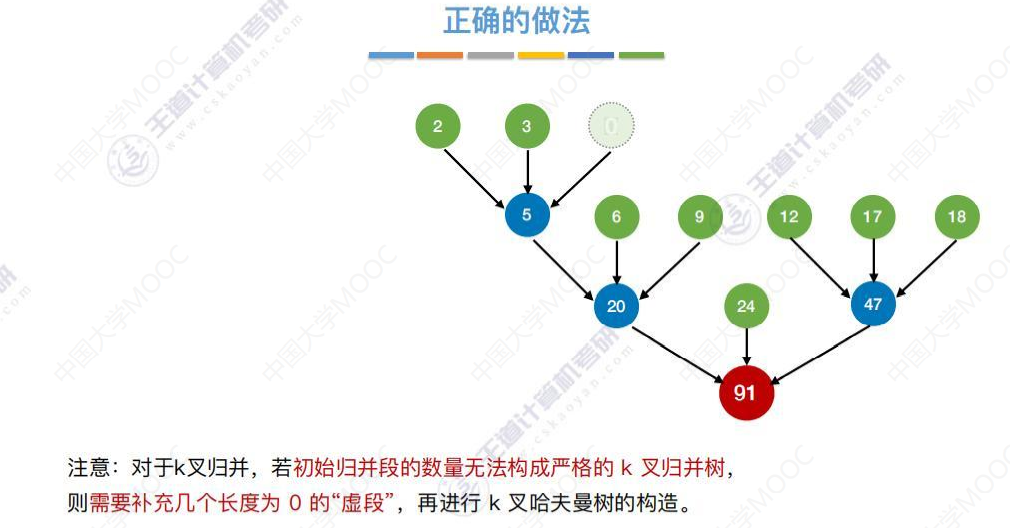
添加虚段的数量

