[数据结构与算法]【数据结构】——栈(Last In First Out)与队列(First In First Out)详解

栈的概念

栈(Last InFirst Out)是一种有着独特元素序列的数据结构，其主要特点就是后进先出，在外面生活中有很多像类型的特征，当浏览网页时，一般都有后退键，这个后退键就运用了栈思想，还有手枪子弹的结构。

栈只能在某一端的插入和删除，满足插入和删除的一端称为栈顶，另一端称为栈底，
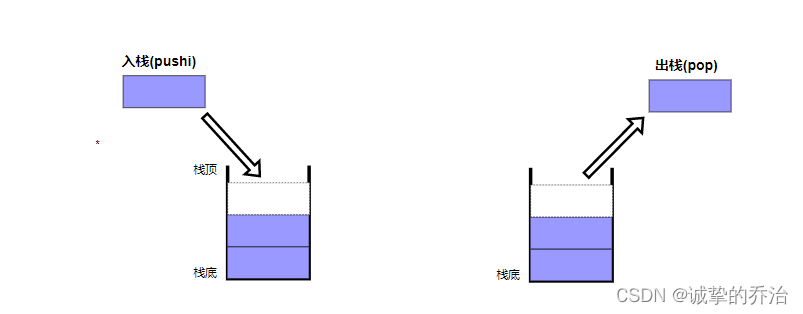
栈的插入过程也叫进栈，也叫压栈，删除过程被称作为出栈

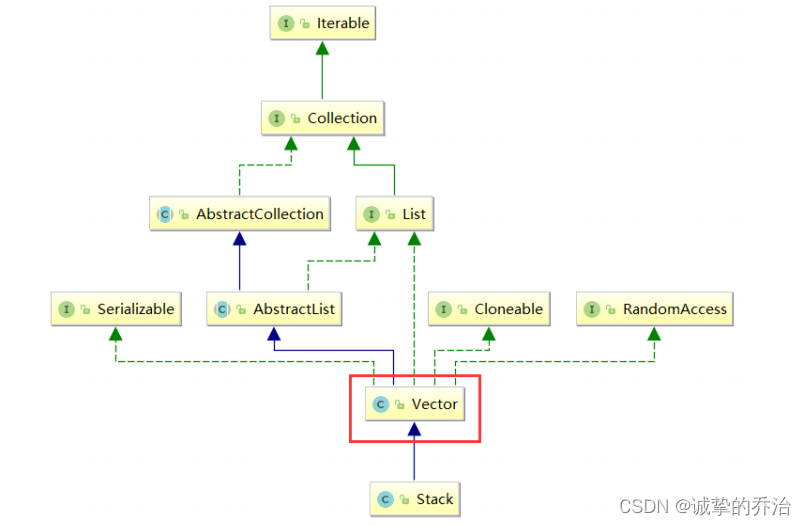
上述集合框架中，Stack时继承Vetor类的，Vector跟ArrayList一样，是一个动态的顺序表，但是Vetor时线程安全的

栈的顺序储存结构与模拟实现

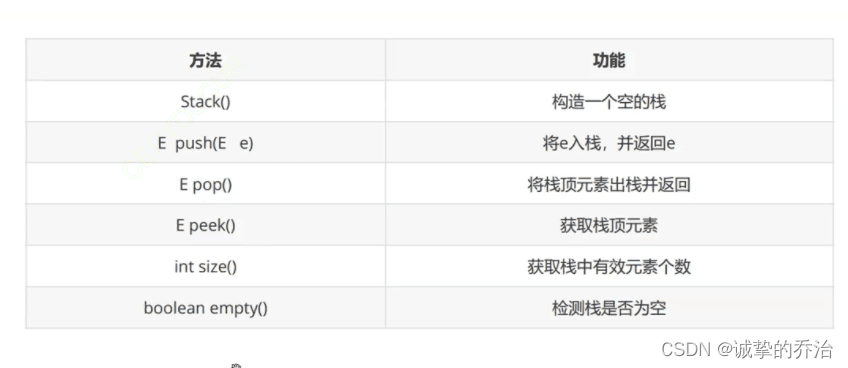
栈的顺序储存结构其底层逻辑时数组，当压栈的过程就是在数组的数组的尾部添加一个元素，其出栈的过程就是将尾部最后一个元素给pop出来。

public class MyStack {
    //用数组实现栈
    private int[] array;
    public int size;

    public MyStack() {
        this.array = new int[3];
    }

    public int push(int e){
        ensureCapacity();
            array[size++] = e;
            return e;
    }

    public int pop(){
        if(empty()) return -1;
        int e = peek();
        size--;
        return e;
    }
    public int peek(){
        if(empty()) throw new RuntimeException("栈为空，无法peek");
        return array[size-1];
    }

    public int size(){
        return size;
    }

    public void ensureCapacity(){
        if(size == array.length){
            this.array = Arrays.copyOf(array,size*2);
        }
    }

    public boolean empty(){
        return size == 0;
    }
}

后缀表达式

后缀表达式也被称之为反波兰表达式，他就是在原有四则运算的基础式子上，经过变化，形成了一种栈结构，可以被计算器所识别，就可以达到连续计算的效果
例如： 中缀表达式( 1 + 2 ) * ( 3 + 4 )
后缀表达式：( ( 1 2 + ) ( 3 4 + ) * )
去掉括号就是：1 2 + 3 4 + *
转变成后缀表达式，适用于栈操作运算，遍历一遍这个字符串，当遇到数字就进行压栈操作，当遇到符号，就进行出栈操作，将栈顶上的两个数字pop出来，并进行相应的运算，得到的结果再次压入栈中，这时候再遍历后续序列的元素，最终栈中的结果就是这个后缀表达式的结果
其代码实现如下：

class Solution {
    public int evalRPN(String[] tokens) {
        Deque<Integer> stack = new LinkedList<Integer>();
        int n = tokens.length;
        for (int i = 0; i < n; i++) {
            String token = tokens[i];
            if (isNumber(token)) {
                stack.push(Integer.parseInt(token));
            } else {
                int num2 = stack.pop();
                int num1 = stack.pop();
                switch (token) {
                    case "+":
                        stack.push(num1 + num2);
                        break;
                    case "-":
                        stack.push(num1 - num2);
                        break;
                    case "*":
                        stack.push(num1 * num2);
                        break;
                    case "/":
                        stack.push(num1 / num2);
                        break;
                    default:
                }
            }
        }
        return stack.pop();
    }

    public boolean isNumber(String token) {
        return !("+".equals(token) || "-".equals(token) || "*".equals(token) || "/".equals(token));
    }
}

队列的概念

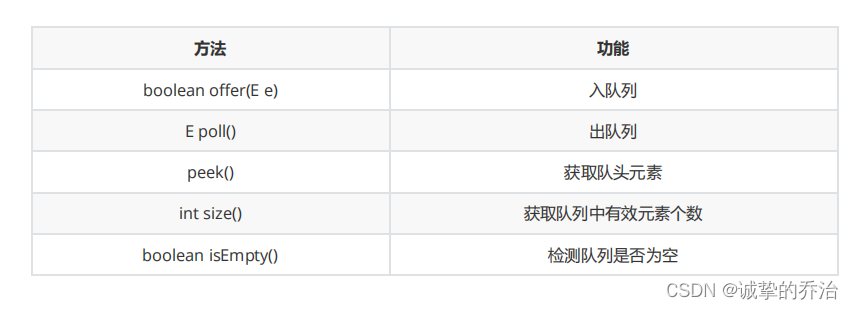
队列(First In First Out)也是一种有这特定序列的数据结构，队列跟栈有一点刚好相反，栈的特点是后进先出，队列的特点就是先进先出，最先进入队列中的元素就最先从队列中拿到

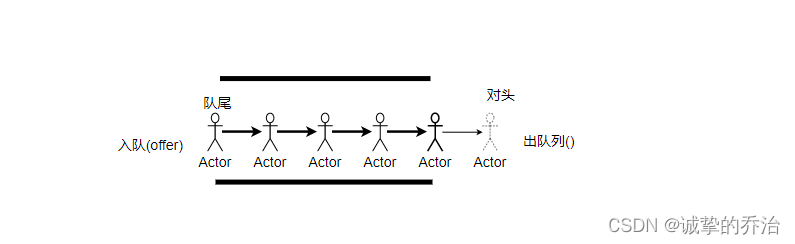
• 执行插入操作的一端被称为队尾，执行删除操作的一端被称之为对头，从队列中拿出数据，交出队列，将数据拿进队列中，被称之为入队。

队列queue的模拟实现

循环队列

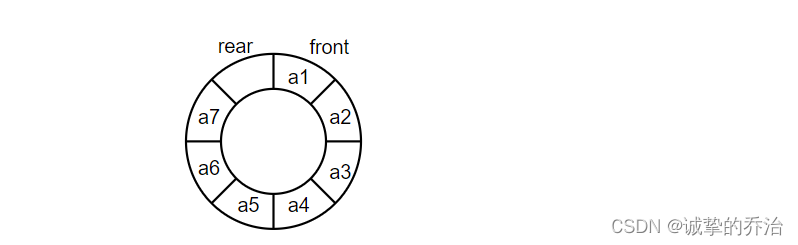
为了方便表示队列的出队和入队操作，需要引入两个变量，其中一个为rear指针，指向的是队列最后一个元素的下一个元素，还有一个是front指针，指向的是首元素的位置，通过操作rear和front可以实现队列的删除和插入操作

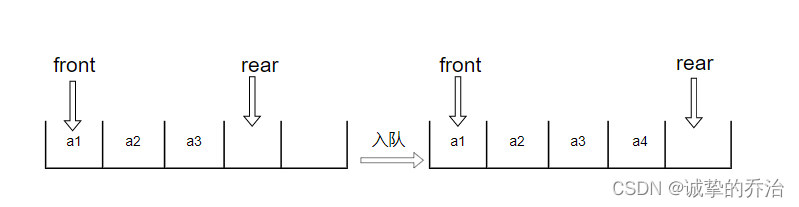
如上图，front指向队列的首元素a1，rear指向的是最后一个元素a3的下一个位置，当插入a4的元素时，向后移一个单位

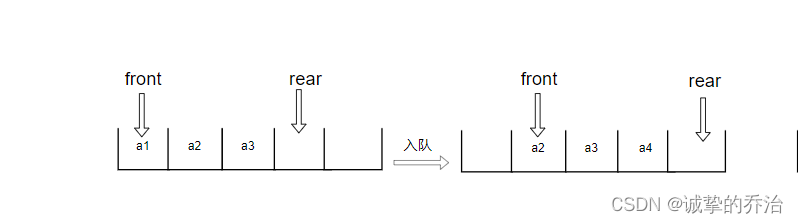
当队列需要出队时，这时候rear的位置就不动，改变front的位置，前进一个单位即可

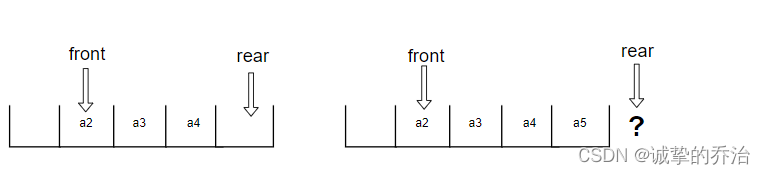
但是如果时上述情况，a5的前面没有空间存放下一个元素，这时候rear已经没有空间可以移动，这个时候就出现了队列的顺序储存结构的弊端
要想充分利用空间，其实让rear指针的指向重新指向前面的位置，循环利用这个空间
如果rear与front相遇，则表示该队列空间为空

这样就形成了循环结构，也就是循环队列
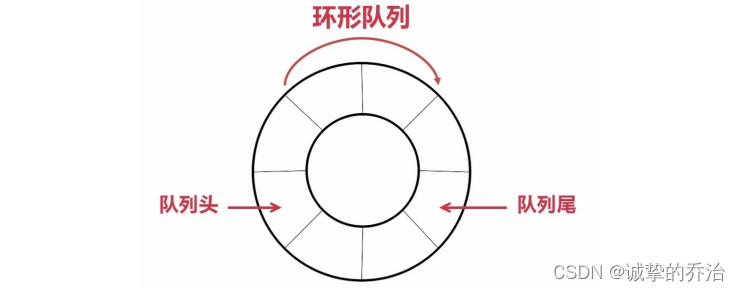怎样判断队列是否已经满了呢

前面说了，当rear与front相遇，则代表队列为空，那判断满了有下面三种方法：

• 利用计数器，当计数器达到队列的容量，则队列已满
• 用flag变量做标记，当rear == front时，flag ==0，则设置为空，当flag == 1时，设置队列为满
• 留一个空间，也就是空一格空间不利用，当rear指针所指向的位置是front的前一个位置，就代表队列已经满了；下面就可以表示队列已满

其代码实现如下：

public class MyCircularQueue {
    //实现循环队列
    private int[] array;
    private int size = 0;
    private int front = 0;
    private int rear = 0;

    public MyCircularQueue(int k) {
        this.array = new int[k];
    }



    public boolean enQueue(int value) {
        if (isFull()) {
            return false;
        }
        array[rear] = value;
        rear = (rear + 1) % array.length;
        size++;
        return true;
    }

    public int Front() {
        if (isEmpty()) return -1;
        return array[front];
    }

    public boolean deQueue(){
        if(isEmpty()){
            return false;
        }
        int temp = array[front];
        front = (front +1 ) % array.length;
        size--;
        return true;
    }

    public int Rear(){
        if(isEmpty())return -1;
        if(rear == 0){
            return array[array.length-1];
        }
        return array[rear-1];
    }

    public boolean isEmpty(){
        return size == 0;
    }

    public boolean isFull(){
        return size == array.length;
    }


    public int size(){
        return size;
    }
}

队列的链式储存结构

这里的链式储存队列，其实就是顺序表的单链表，只不过他只能尾进头出，称为链队列，为了操作操作方便，将对头对象单链表的头结点，队尾指向单链表的尾部
与单链表不一样的是，链表的尾部引入尾结点，方便后续的入队操作，实现O(1)时间复杂度的算法。具体代码如下：

public class MyQueue {
    private int size = 0;
    private Node head = null; private Node last = null;
    static class Node{
        int val;//数据域
        Node next = null;
        public Node(int val) {
            this.val = val;
        }//构造函数，初始化数据域
    }

    public boolean offer(int k){
        Node cur = new Node(k);
        if(head == null){
            head = cur;
            last = cur;
            size++;
            return true;
        }
        last.next = cur;
        last = cur;
        size++;
        return true;
    }

    public int poll(){
        if(isEmpty()){
            return -1;
        }
        int temp = head.val;
        head = head.next;
        size--;
        return temp;
    }

    public int peek(){
        if(isEmpty()){
            return -1;
        }
        return head.val;
    }

    public int size(){
        return size;
    }

    public boolean isEmpty(){
        return size == 0;
    }
}

栈与队列的意义

在数组和链表功能如此强大的基础上，为什么要单独拎出来栈与队列的数据结构呢，在很多时候，我们需要的操作可能只是链表，数组功能的一部分，栈与队列简化了程序设计问题，让思考的范围减少，使我们聚焦在问题的本质上，换言之如果我们把时间花在数组下标的选择问题上，就会分散我们的思考，也就是栈与队列的意义。