大纲
1.引入
2.Kahn算法
3.DFS求拓扑排序
4.例题
1. 引入
引入:
?
【问题描述】topsort大学计算机系正在尝试一种新的教学方式:“学生可以自行选择课程的
学习顺序”,但是有的课程可能会依赖其他课程,比如《数据结构》要依赖《程序设计》
的知识,那么在学习《数据结构》之前就必须学习《程序设计》,依赖关系如下图(A到B
的箭头表示学习A以后才可以学习B),请帮助学生小T设计一条可行的学习路线。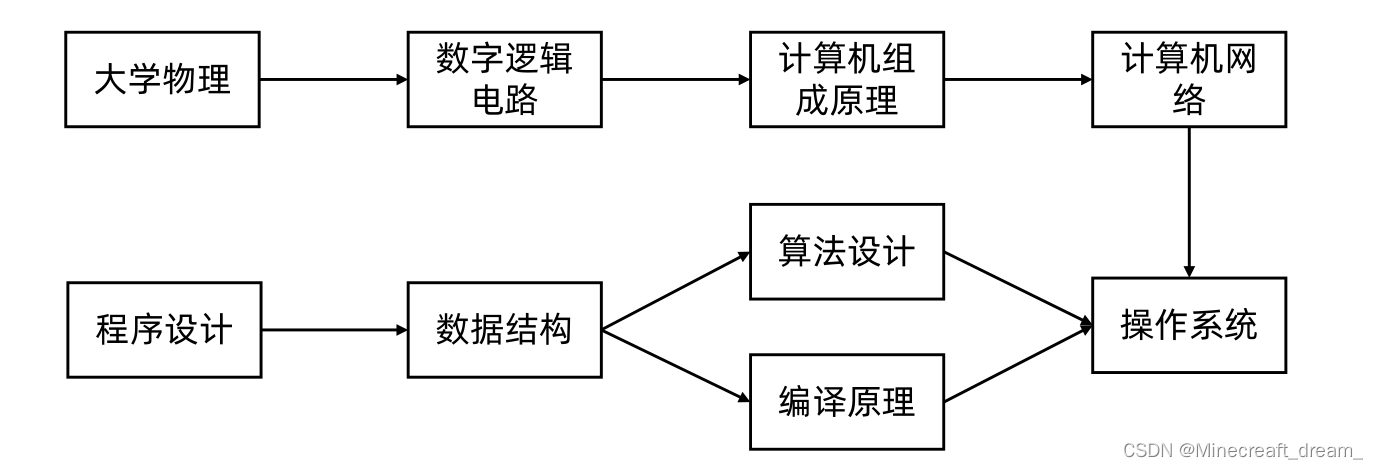
?
对于一个有向无环(V,E)来说,其拓扑排序是G中所有顶点的一种线性次序,该次序满
足如下条件:如果图G包含边(u,v) ,则节点u在拓扑排序中处于v的前面(如果图G包含环
路,则不可能排出一个线性次序)。
注意:拓扑排序不是唯一的。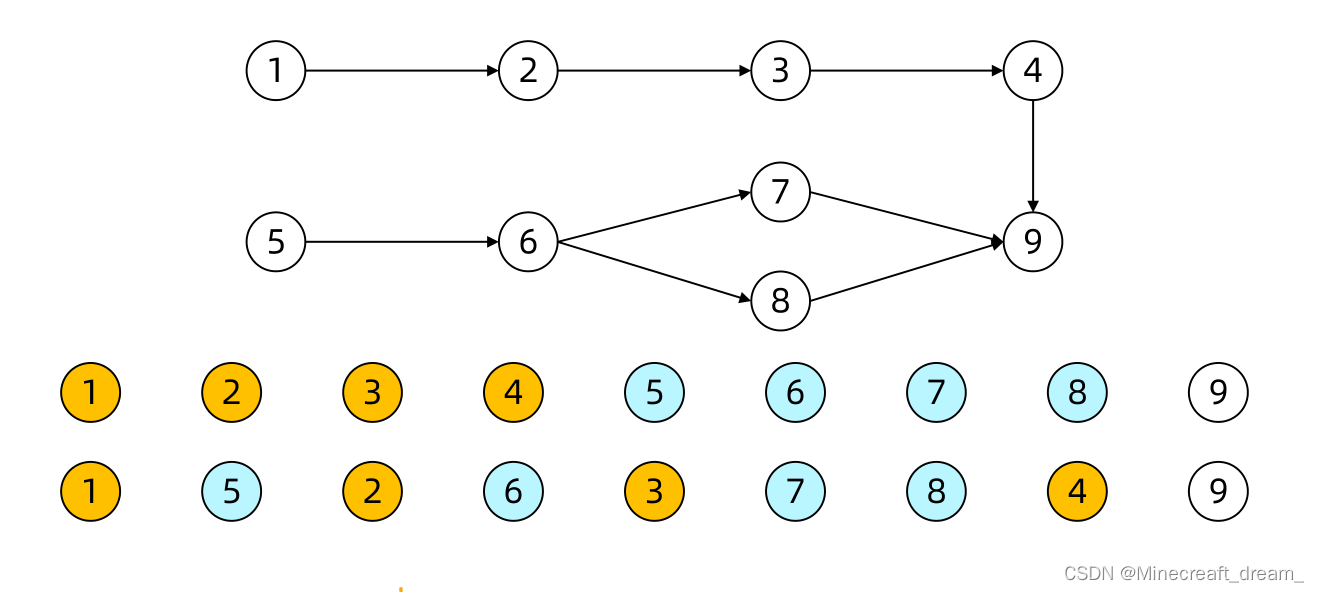
2.Kahn算法
算法思想:每次找到一个入度为0的顶点,删除该顶点及其所有的出弧。

?【Kahn判断环】
通过Kahn算法判断图中是否有环。
还有未处理的顶点,但是已经没有入度为0的顶点了。

?算法过程
Kahn算法求有向图G(V,E)的拓扑排序。
① 从有向图G中任选一个入度为0的顶点v输出。
② 从有向图G中删除顶点v,以及所有以v为起点的弧,即删除v的所有出弧。
③ 重复①和②,直到图G中不存在入度为0的顶点,如果此时图G中还有顶点没有处理,则
可以判定有向图G中存在环。
?如何查找拥有N个顶点, M条边的有向图G(V,E)中入度为0的顶点?
枚举:邻接矩阵每次查找时间复杂度O(N^2) ,总时间复杂度:O(N^3) ;邻接表每次查找时
间复杂度O(M),总时间复杂度O(NM)。
枚举+数组标记:定义辅助数组in[N] , in[i] 记录顶点i的入度,删边时更新in数组,每次
查询时间复杂度O(N),修改的总时间复杂度O(M),总时间复杂度O(N^2 + M)
数组标记+队列:定义辅助数组in[N] , in[i] 记录顶点i的入度,将所有入度为0的顶点加
入队列,删边时更新in数组,并将入度为0的顶点加入队列,每次查询时间复杂度O(1),
总修改时间复杂度O(M),总时间复杂度O(N + M)。
?
使用Kahn算法求有向图G(V,E)的拓扑排序,如何输出字典序最小的拓扑排序?
如要输出字典序最小的拓扑排序,需要保证每次输出的顶点都是当前入度为0的顶点
中编号最小的。只需要将队列修改为优先队列(小根堆),即可确保每次输出都是
当前所有入度为0的顶点中编号最小的。
优先队列查询复杂度:O(1),修改复杂度O(log(n)) , 总复杂度:O(N + M + Nlog(N))
3.DFS求拓扑排序
在对树进行深度优先遍历时,对于每个节点,在刚进入递归时,以及即将回溯前各记录一次该
点,最后产生的长度为2N的节点序列称为树的DFS序。
DFS序的特点:每个节点x在序列中都恰好出现两次,设这两次出现的位置分别为in[x]和
out[x] ,那么闭区间[in[x],out[x]]就是以x为根的子树的DFS序。以顶点v为起点对有向无环图G(V,E)进行深度优先搜索的过程中,v的所有后继顶点一定会
先于v完成退出,在拓扑排序中v应该排在其所有后继顶点的前面,所以可以在dfs(v)退出
时将v加入拓扑序列的最前面。
?使用DFS进行拓扑排序时,DFS以任何顺序都可以。
是否可以在dfs(v)进入时将v加入到拓扑序的尾部?
不可以,因为按上述策略,从任意顶点v进行dfs时,可以保证v的后继顶点都会排
在v的后面,但是无法保证v的前驱顶点都排在v的前面。
?算法过程:
DFS算法求有向图𝐺(𝑉,𝐸)的拓扑排序。
① 从有向图𝐺中任意一个还未访问的顶点v出发进行dfs(v)操作。
② 在dfs(v)完成退出前,将v加入拓扑序列的最前面。
③ 重复①和②,直到图G中所有顶点都被访问。
【DFS判断环】
使用DFS判断有向图中是否有环。
从任意顶点v出发进行dfs(v) ,如果在该次递归dfs过程中v又被访问则存在环。
vis数组增加一个值, vis[v] == 0表示顶点v还未访问,当dfs(v)进入时标记vis[v]=-1。在
接下来的dfs递归过程中如果再次访问到v,则说明图中存在环。当dfs(v)退出时标记vis[v]=1表示顶点v已访问。从任意顶点v出发进行dfs(v) ,如果在该次递归过程中v又被访问则存在环。
vis数组增加一个值, vis[i] == 0表示顶点i还未访问, vis[i] == 1表示在之前的dfs过程中已
被访问,vis[i]? == -1,表示i在dfs(i)的过程中已被访问,如果出现vis值为-1的节点再次被
访问到,说明图中存在环。?
?4.例题
【题目描述】
FJ打算拓展他的牛奶销售市场。他打算将牛奶销售拓展到编号为1...N的N个城镇(1 <= N <= 25000)。这些城镇通过编号为1..R的R(1 <= R <= 50,000)条道路和(或)编号为1...P的P(1 <= P <= 50,000)条航线相连。每条道路i连接城镇A_i和B_i,花费为C_i。
对于道路0 <= C_i <= 10000,然而航线的花费很奇怪,花费C_i可能是负数(-10000 <= C_i <= 10000)。道路是双向的,可以从A_i到B_i,也可以从B_i到A_i。航线是单向的,只能从A_i到B_i,而且由于航班管控,如果有一条航线从A_i到B_i,那么一定不可能通过一些道路和航线从B_i到A_i。
由于FJ的牛奶很受欢迎,所有的城镇都订购了他的牛奶。他想知道从中心城镇S(1<=S<=N)把牛奶分别送到每个城镇的最低花费。或者知道那是不可能的。
输入格式
第1行:4个空格分隔的整数N, R, P, S,分别表示城镇的数量,道路的数量,航线的数量和中心城镇的编号。
第2号到第R+1行:每行3个空格分隔的整数A_i, B_i和C_i,描述一条道路信息。
第R+2行到R+P+1行:每行3个空格分隔的整数A_i, B_i和C_i,描述一条航线信息。
输出格式
共N行,第i行输出从中心城镇S到城镇i的最小花费,如果不能到达,输出"NO PATH"。
输入输出样列
输入样例1:
6 3 3 4
1 2 5
3 4 5
5 6 10
3 5 -100
4 6 -100
1 3 -10
输出样例1:
NO PATH
NO PATH
5
0
-95
-100 🔑思路
由于图中有负边,所以无法使用Dijkstra直接求解,Bellman-Ford算法时间复杂度:O(VE)
直接使用Bellman-Ford求解会超时!
由于道路是双向的,在不考虑航线的情况下,N个顶点可以组成M个连通子图。
例如:样例1中,6个顶点共形成3个连通子图。
考虑任意两个连通子图A和B ,如果A中有到达B的航线,那么B一定没有到达A的路线。
证明: 证明:假设A中的顶点i到B中的顶点j有航线,如果B中有到达A的路线,设B中的x到A中的y有路线,那么j可以通过j → x → y → y到达y,这和题意不符。
将每个连通子图缩成一个点,连通子图之间构成一个有向无环图。
每个连通子图都只能通过有限的航线进入,只有有航线的顶点的最短路可能由其上一个连通
子图中的顶点更新,所有没有航线的顶点的最短路一定是由连通子图的入口点更新。所以如
果知道了每个有航班顶点的最短路,那么连通子图内部其他的节点可以通过Dijkstra求解。
DAG上最短路的求解顺序和其拓扑序保持一致,拓扑序排在S所属连通子图前面的顶点都
不存在最短路,如上例中连通子图1中的顶点1和2不存在最短路。
按照拓扑序的顺序求解各个连通子图的最短路,连通子图内部的最短路由其入口顶点更
新,入口顶点的最短路由航线的起点更新。