[数据结构与算法]双指针技巧解决链表、数组中的问题

链表

合并有序链表

21. 合并两个有序链表 - 力扣（LeetCode）

非常简单的一道题目，初步可以体会到双指针的使用方法

此外如果使用虚拟头节点（dummy）可以避免处理空指针的情况，最后返回 dummuy.next就行了

合并k个有序链表

23. 合并K个升序链表 - 力扣（LeetCode）

难点在于，如何快速得到 k 个节点中的最小节点，接到结果链表上

一个优化方法是用到 **优先级队列（二叉堆）**这种数据结构，把链表节点放入一个最小堆，就可以每次获得 k 个节点中的最小节点

还有一种优化方法是分治合并两两链表

单链表的倒数第 k 个节点

一般题目只会给我们头节点，我们需要先遍历一次得到节点数量n，再次遍历结算 n - k + 1个节点，但如果我们使用两个指针就能一次遍历，只需要 p_1指针先走k个结点即可

判断链表是否包含环

每当慢指针 slow 前进一步，快指针 fast 就前进两步。

如果 fast 最终遇到空指针，说明链表中没有环；如果 fast 最终和 slow 相遇，那肯定是 fast 超过了 slow 一圈，说明链表中含有环。

如果链表中含有环，如何计算这个环的起点？

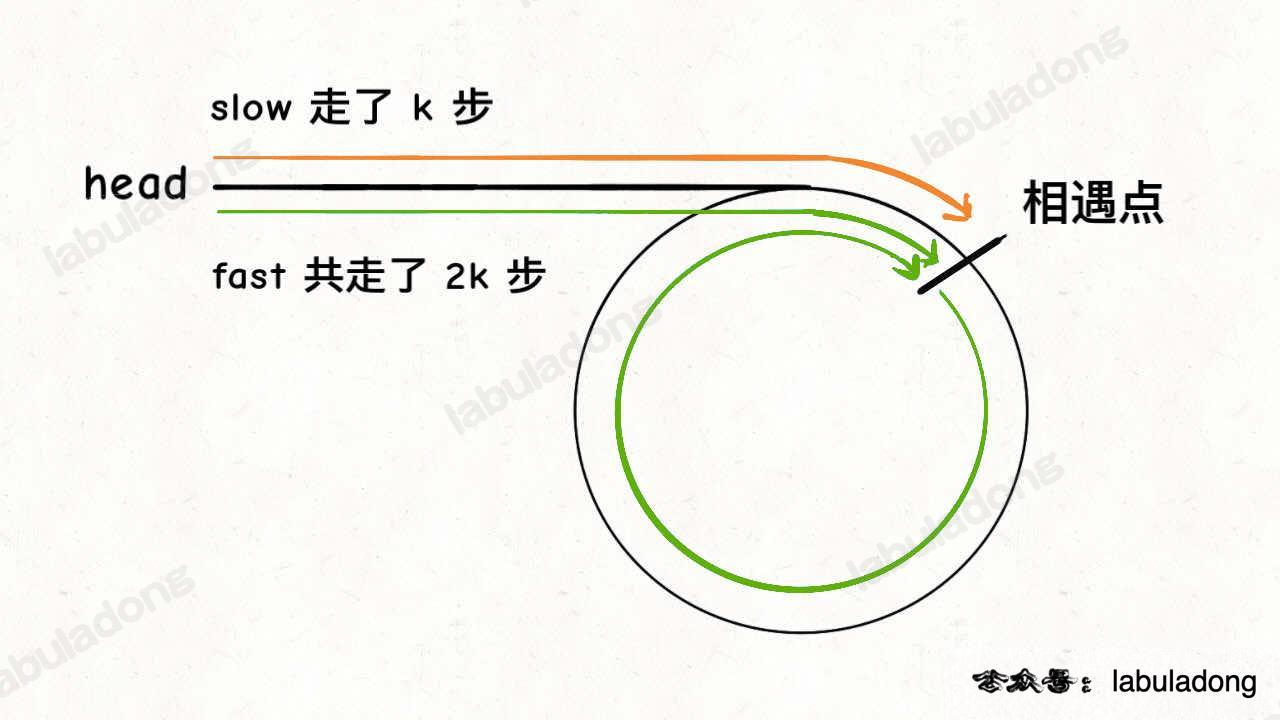
假设相遇点和环的起点距离为m，又因slow走了k步，所以头节点与环的起点距离为k - m。

因为fast比 slow 多走了k步 ， k 一定是环长度的整数倍，所以 fast 走 k - m步到达环节点

所以当快慢指针相遇时，让其中任一个指针指向头节点，然后让它俩以相同速度前进，再次相遇时所在的节点位置就是环开始的位置

两个链表是否相交

160. 相交链表 - 力扣（LeetCode）

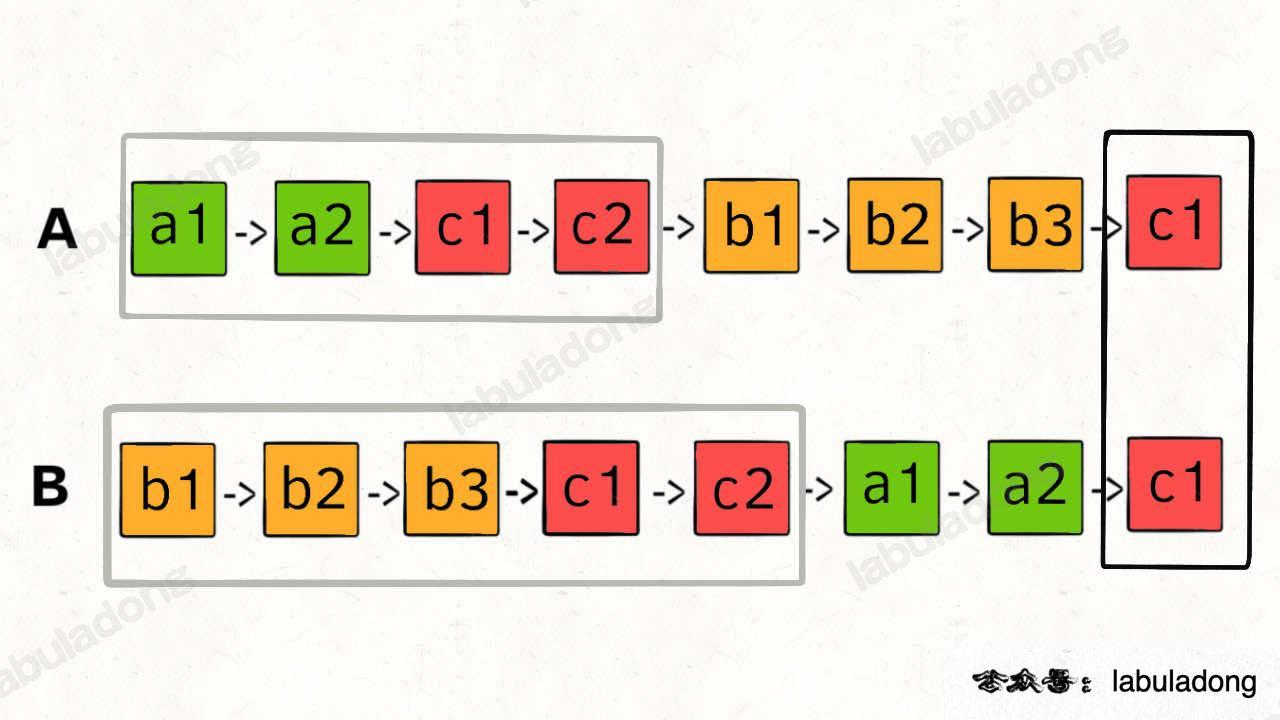
我们可以让 p1 遍历完链表 A 之后开始遍历链表 B，让 p2 遍历完链表 B 之后开始遍历链表 A，这样相当于「逻辑上」两条链表接在了一起。

这样进行拼接，就可以让 p1 和 p2 同时进入公共部分，也就是同时到达相交节点 c1

如果把两条链表首尾相连，那么「寻找两条链表的交点」的问题转换成了前面讲的「寻找环起点」的问题

数组

快慢指针

我们可以把索引当做数组中的指针，这样也可以在数组中施展双指针技巧

数组问题中比较常见的快慢指针技巧，是让你原地修改数组

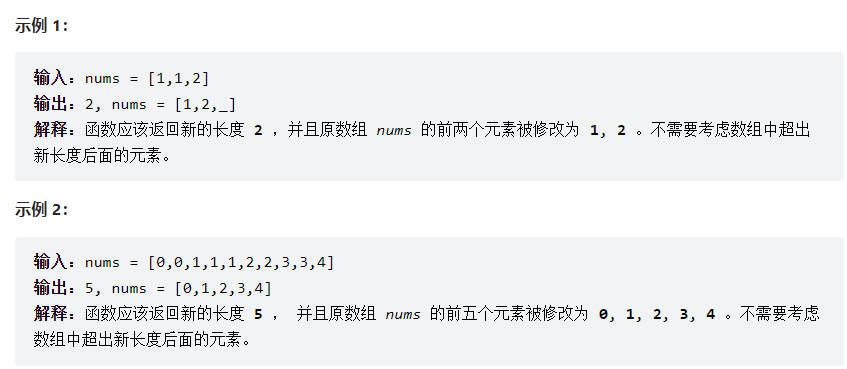
删除有序数组中的重复项

26. 删除有序数组中的重复项 - 力扣（LeetCode）

找到一个不重复的元素就赋值给 slow 并让 slow 前进一步。

这样，就保证了 nums[0..slow] 都是无重复的元素，当 fast 指针遍历完整个数组 nums 后，nums[0..slow] 就是整个数组去重之后的结果

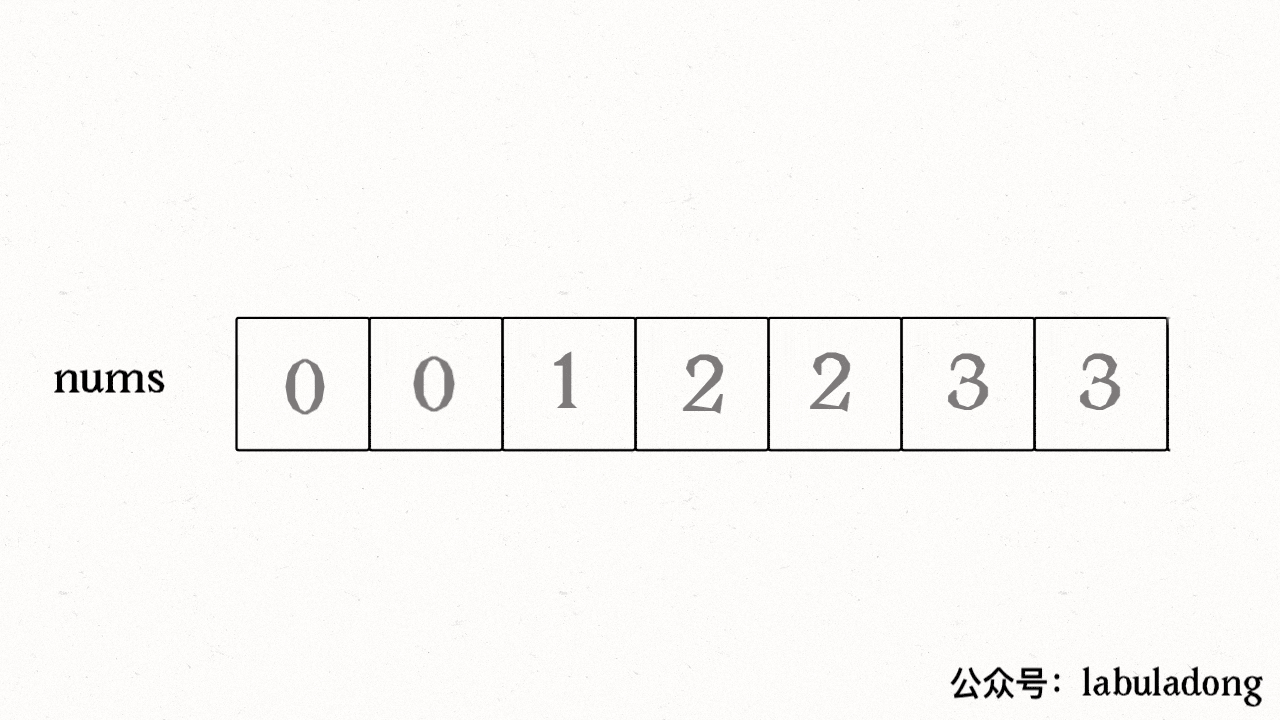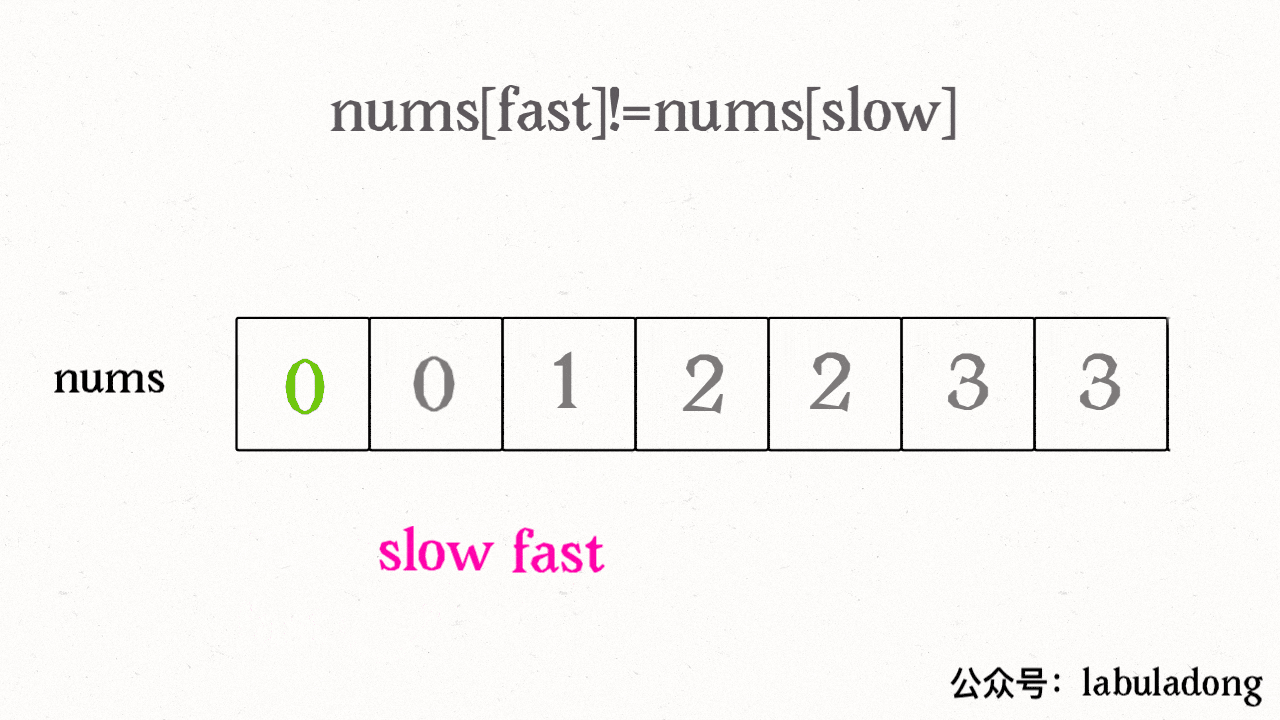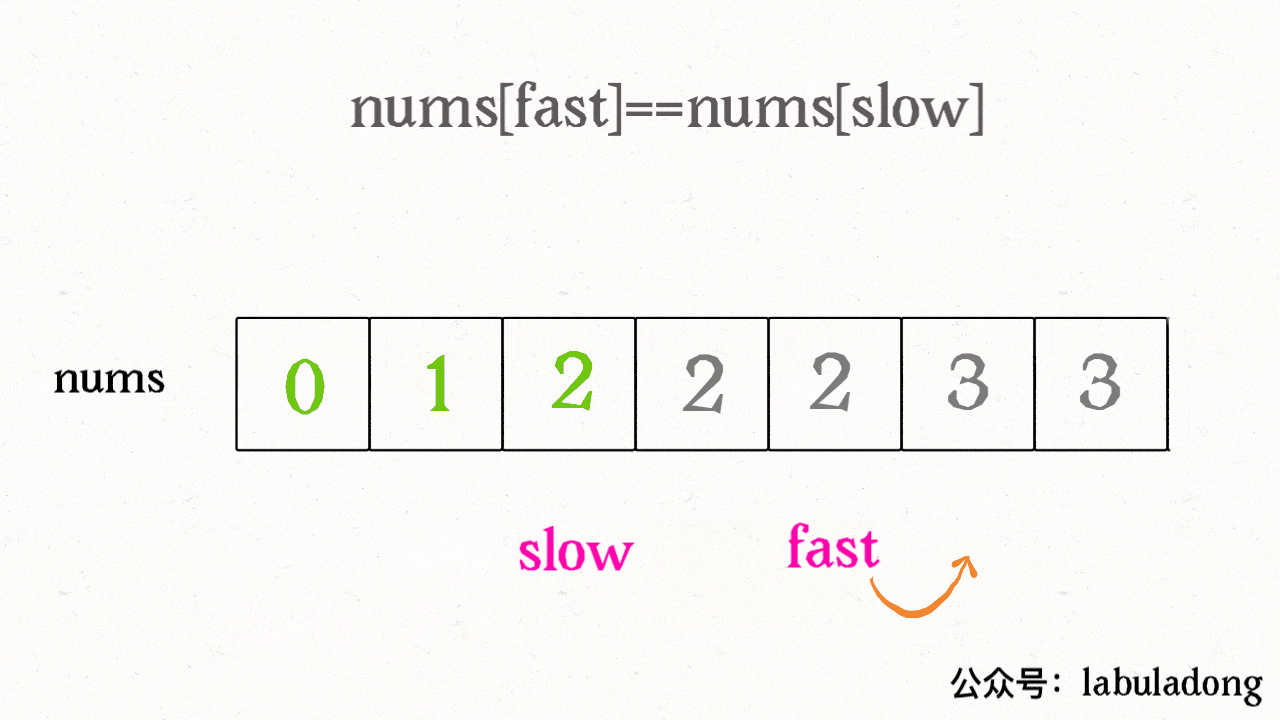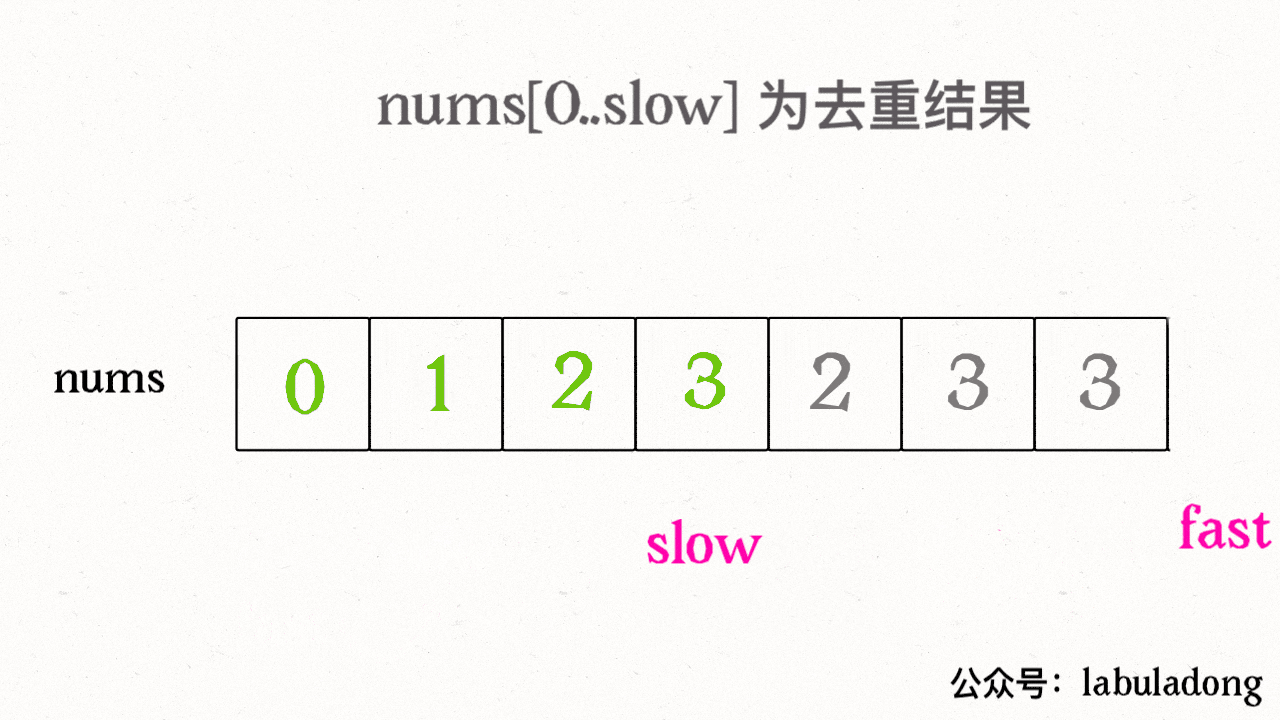
同样的83. 删除排序链表中的重复元素 - 力扣（LeetCode）也是这样的思路

移动零

283. 移动零 - 力扣（LeetCode）

给定一个输入数组 nums，请你原地修改，将数组中的所有值为 0 的元素移到数组末尾

fast指针遇到value = 0的元素就跳过，不等于0就赋值给slow指针，最后再将剩余控制全部赋值为0即可

滑动窗口

初始化 left = right = 0，把索引左闭右开区间 [left, right) 称为一个「窗口」

因为这样初始化 left = right = 0 时区间 [0, 0) 中没有元素，但只要让 right 向右移动（扩大）一位，区间 [0, 1) 就包含一个元素 0 了。

/* 滑动窗口算法框架 */
void slidingWindow(string s, string t) {
    unordered_map<char, int> need, window;
    for (char c : t) need[c]++;
    
    int left = 0, right = 0;
    int valid = 0; 
    while (right < s.size()) {
        char c = s[right];
        // 右移（增大）窗口
        right++;
        // 进行窗口内数据的一系列更新
        //...

        while (window needs shrink) {
            char d = s[left];
            // 左移（缩小）窗口
            left++;
            // 进行窗口内数据的一系列更新
            //...
        }
    }
}

套模板需要思考以下几个问题：

1. 什么时候应该移动 right 扩大窗口？窗口加入字符时，应该更新哪些数据？
2. 什么时候窗口应该暂停扩大，开始移动 left 缩小窗口？从窗口移出字符时，应该更新哪些数据？
3. 我们要的结果应该在扩大窗口时还是缩小窗口时进行更新？

最小覆盖子串

76. 最小覆盖子串 - 力扣（LeetCode）

给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 “” 。

注意：

? 对于 t 中重复字符，我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
? 如果 s 中存在这样的子串，我们保证它是唯一的答案。

我们先增加right直到窗口包含了t中所有的字符，然后不断缩小left

字符串排列

567. 字符串的排列 - 力扣（LeetCode）

给你两个字符串 s1 和 s2 ，写一个函数来判断 s2 是否包含 s1 的排列。如果是，返回 true ；否则，返回 false 。

换句话说，s1 的排列之一是 s2 的 子串

这种题目，是明显的滑动窗口算法，相当给你一个 S 和一个 T，请问你 S 中是否存在一个子串，包含 T 中所有字符且不包含其他字符

// 判断 s 中是否存在 t 的排列
bool checkInclusion(string t, string s) {
    unordered_map<char, int> need, window;
    //unordered_map 就是哈希表（字典）
    //它的一个方法 count(key)  可以判断键 key 是否存在
    for (char c : t) need[c]++;
    //如果该 key 不存在，C++ 会自动创建这个 key，并把 map[key] 赋值为 0
    
    int left = 0, right = 0;
    int valid = 0;
    while (right < s.size()) {
        char c = s[right];
        right++;
        // 进行窗口内数据的一系列更新
        if (need.count(c)) {
            window[c]++;
            if (window[c] == need[c])
                valid++;
        }

        // 判断左侧窗口是否要收缩
        while (right - left >= t.size()) {
            // 在这里判断是否找到了合法的子串
            if (valid == need.size())
                return true;
            char d = s[left];
            left++;
            // 进行窗口内数据的一系列更新
            if (need.count(d)) {
                if (window[d] == need[d])
                    valid--;
                window[d]--;
            }
        }
    }
    // 未找到符合条件的子串
    return false;
}

找到字符串中所有字母异味词

438. 找到字符串中所有字母异位词 - 力扣（LeetCode）

给定两个字符串 s 和 p，找到 s 中所有 p 的 异位词 的子串，返回这些子串的起始索引。不考虑答案输出的顺序。

异位词 指由相同字母重排列形成的字符串（包括相同的字符串）。

相当于，输入一个串 S，一个串 T，找到 S 中所有 T 的排列，返回它们的起始索引。

跟寻找字符串的排列一样，只是找到一个合法异位词（排列）之后将起始索引加入 res 即可

总结

遇到子数组/子串相关的问题，你只要能回答出来以下几个问题，就能运用滑动窗口算法：

1、什么时候应该扩大窗口？

2、什么时候应该缩小窗口？

3、什么时候得到一个合法的答案？

左右指针

二分查找

这里只写最简单的二分算法，旨在突出它的双指针特性

int binarySearch(int[] nums, int target) {
    // 一左一右两个指针相向而行
    int left = 0, right = nums.length - 1;
    while(left <= right) {
        int mid = (right + left) / 2;
        if(nums[mid] == target)
            return mid; 
        else if (nums[mid] < target)
            left = mid + 1; 
        else if (nums[mid] > target)
            right = mid - 1;
    }
    return -1;
}

n数之和

两数之和

假设输入一个数组 nums 和一个目标和 target，请你返回 nums 中能够凑出 target 的两个元素的值

注意：

nums 中可能有多对儿元素之和都等于 target，请你的算法返回所有和为 target 的元素对儿，其中不能出现重复。

vector<vector<int>> twoSumTarget(vector<int>& nums, int target) {
    // nums 数组必须有序
    sort(nums.begin(), nums.end());
    int lo = 0, hi = nums.size() - 1;
    vector<vector<int>> res;
    while (lo < hi) {
        int sum = nums[lo] + nums[hi];
        int left = nums[lo], right = nums[hi];
        if (sum < target) {
            //跳过重复元素
            while (lo < hi && nums[lo] == left) lo++;
        } else if (sum > target) {
            while (lo < hi && nums[hi] == right) hi--;
        } else {
            res.push_back({left, right});
            while (lo < hi && nums[lo] == left) lo++;
            while (lo < hi && nums[hi] == right) hi--;
        }
    }
    return res;
}

n Num之和

三个数之和为target，我们穷举数组当中的数，对于每个不重复得元素都使用上述两数之和得解决方案

四数之和，我们穷举数组当中的数，对于每个不重复得元素都使用上述三数之和得解决方案

从这里我们就能看出一点规律了，n个数之和就是穷举加上n - 1个数之和

/* 注意：调用这个函数之前一定要先给 nums 排序 */
vector<vector<int>> nSumTarget(
    vector<int>& nums, int n, int start, int target) {

    int sz = nums.size();
    vector<vector<int>> res;
    // 至少是 2Sum，且数组大小不应该小于 n
    if (n < 2 || sz < n) return res;
    // 2Sum 是 base case
    if (n == 2) {
        // 双指针那一套操作
        int lo = start, hi = sz - 1;
        while (lo < hi) {
            int sum = nums[lo] + nums[hi];
            int left = nums[lo], right = nums[hi];
            if (sum < target) {
                while (lo < hi && nums[lo] == left) lo++;
            } else if (sum > target) {
                while (lo < hi && nums[hi] == right) hi--;
            } else {
                res.push_back({left, right});
                while (lo < hi && nums[lo] == left) lo++;
                while (lo < hi && nums[hi] == right) hi--;
            }
        }
    } else {
        // n > 2 时，递归计算 (n-1)Sum 的结果
        for (int i = start; i < sz; i++) {
            vector<vector<int>> 
                sub = nSumTarget(nums, n - 1, i + 1, target - nums[i]);
            for (vector<int>& arr : sub) {
                // (n-1)Sum 加上 nums[i] 就是 nSum
                arr.push_back(nums[i]);
                res.push_back(arr);
            }
            while (i < sz - 1 && nums[i] == nums[i + 1]) i++;
        }
    }
    return res;
}