动态规划
为什么有这个话题,由一个问题而来
问题
给你一个由 无重复 正整数组成的集合 nums ,请你找出并返回其中最大的整除子集 answer ,子集中每一元素对 (answer[i], answer[j]) 都应当满足:
-
answer[i] % answer[j] == 0 ,或
-
answer[j] % answer[i] == 0
如果存在多个有效解子集,返回其中任何一个均可。
示例 1:
输入:nums = [1,2,3]
输出:[1,2]
解释:[1,3] 也会被视为正确答案。
示例 2:
输入:nums = [1,2,4,8]
输出:[1,2,4,8]
我的解答
思路一
先找出有倍数关系的结果,然后找出能除尽有倍数关系的每一个元素,如果结果是每一个元素的倍数,那么把这个结果添加到结果中,这样这个列表会越来越长,看是否能得到最终的结果
func largestDivisibleSubset(nums []int) []int {
var answer []int
ins := false
OuterLoop:
for i:=0;i<len(nums);i++{
for j:=i+1;j<len(nums);j++{
if nums[i] % nums[j] == 0 || nums[j] % nums[i] == 0{
answer = append(answer, nums[i], nums[j])
ins = true
break OuterLoop;
}
}
}
if ins{
for _,num := range nums{
ok := true
for _,ans := range answer{
if num % ans != 0{
ok = false
break
}
}
if ok{
in := false
for _,obj := range answer{
if num == obj{
in = true
}
}
if !in{
answer = append(answer,num)
}
}
}
}
if len(answer) == 0 && len(nums) >= 0{
answer = []int{nums[0]}
}
return answer
}
结果:21 / 48 个通过测试用例
输入
[3,4,16,8]
输出
[4,16]
预期结果
[4,8,16]
思路二
既然要求最大长度的整除子集,那么就先将它排序,排序后计算首位的倍数,假订首位一定是因数。
func largestDivisibleSubset(nums []int) []int {
for i := 1;i<len(nums);i++{
tmpv := nums[i]
j := i-1
for ;j >= 0 && nums[j] > tmpv;j--{
nums[j+1] = nums[j]
}
nums[j+1] = tmpv
}
if len(nums) <= 1{
return nums
}
answer := []int{nums[0]}
for _,num := range nums[1:len(nums)]{
ok := true
for _,ans := range answer{
if num % ans != 0{
ok = false
break
}
}
if ok{
answer = append(answer, num)
}
}
return answer
}
结果:34 / 48 个通过测试用例
输入
[3,4,16,8]
输出
[3]
预期结果
[4,8,16]
思路三
既然最小的数不一定是因子,那么就枚举每一个对象,假订每一个数都可能是最小因子,然后选出最优
func largestDivisibleSubset(nums []int) []int {
for i := 1;i<len(nums);i++{
tmpv := nums[i]
j := i-1
for ;j >= 0 && nums[j] > tmpv;j--{
nums[j+1] = nums[j]
}
nums[j+1] = tmpv
}
if len(nums) <= 1{
return nums
}
var res []int
for i:=0;i<len(nums);i++{
answer := []int{nums[i]}
for j:=i+1;j<len(nums);j++{
ok := true
for _,ans := range answer{
if nums[j] % ans != 0{
ok = false
break
}
}
if ok{
answer = append(answer, nums[j])
}
}
if len(answer) > len(res){
res = answer
}
}
return res
}
结果:39 / 48 个通过测试用例
输入
[5,9,18,54,108,540,90,180,360,720]
输出
[5,90,180,360,720]
预期结果
[9,18,90,180,360,720] //枚举到9时,命中了[9,18,54,108,540],和结果一样长
思路四
既然有可能是跳过某个对象的,那么排序就没有用呀,不如直接枚举每个对象为可能是最小公因数,然后找出最长的,当相等时,不加入到最优的列表
func largestDivisibleSubset(nums []int) []int {
if len(nums) <= 1{
return nums
}
var arr []int
for i:=0;i<len(nums);i++{
obj := []int{nums[i]}
fmt.Println("---",obj)
for j:=0;j<len(nums);j++{
ok := true
for _,ans := range obj {
if ans % nums[j] != 0 && nums[j] % ans != 0{
ok = false
break
}
}
if ok && nums[j] != obj[0]{
obj = append(obj, nums[j])
}
}
if len(obj)>len(arr){
arr = obj
}
}
for i := 1;i<len(arr);i++{
tmpv := arr[i]
fmt.Println(arr[i])
j := i-1
for ;j >= 0 && arr[j] > tmpv;j--{
arr[j+1] = arr[j]
}
arr[j+1] = tmpv
}
return arr
}
结果:43 / 48 个通过测试用例
输入
[5,9,18,54,108,540,90,180,360,720]
输出
[9,18,54,108,540]
预期结果
[9,18,90,180,360,720]
思路五
看没有通过的测试用例,如果从最大开始找,那么是可以将最长记录找出来的
func sortArr(nums []int)[]int{
for i := 1;i<len(nums);i++{
tmpv := nums[i]
j := i-1
for ;j >= 0 && nums[j] > tmpv;j--{
nums[j+1] = nums[j]
}
nums[j+1] = tmpv
}
return nums
}
func largestDivisibleSubset(nums []int) []int {
if len(nums) <= 1{
return nums
}
nums = sortArr(nums)
var arr []int
for i:=len(nums)-1;i>-1;i--{
ins := nums[i]
answer := []int{ins}
for j:=i-1;j > -1;j--{
if ins % nums[j] == 0{
answer = append(answer, nums[j])
ins = nums[j]
}
}
fmt.Println(sortArr(answer))
if len(arr) < len(answer){
arr = answer
}
}
return sortArr(arr)
}
结果:45 / 48 个通过测试用例
输入
[4,8,10,240]
输出
[10,240]
预期结果
[4,8,240]
总结
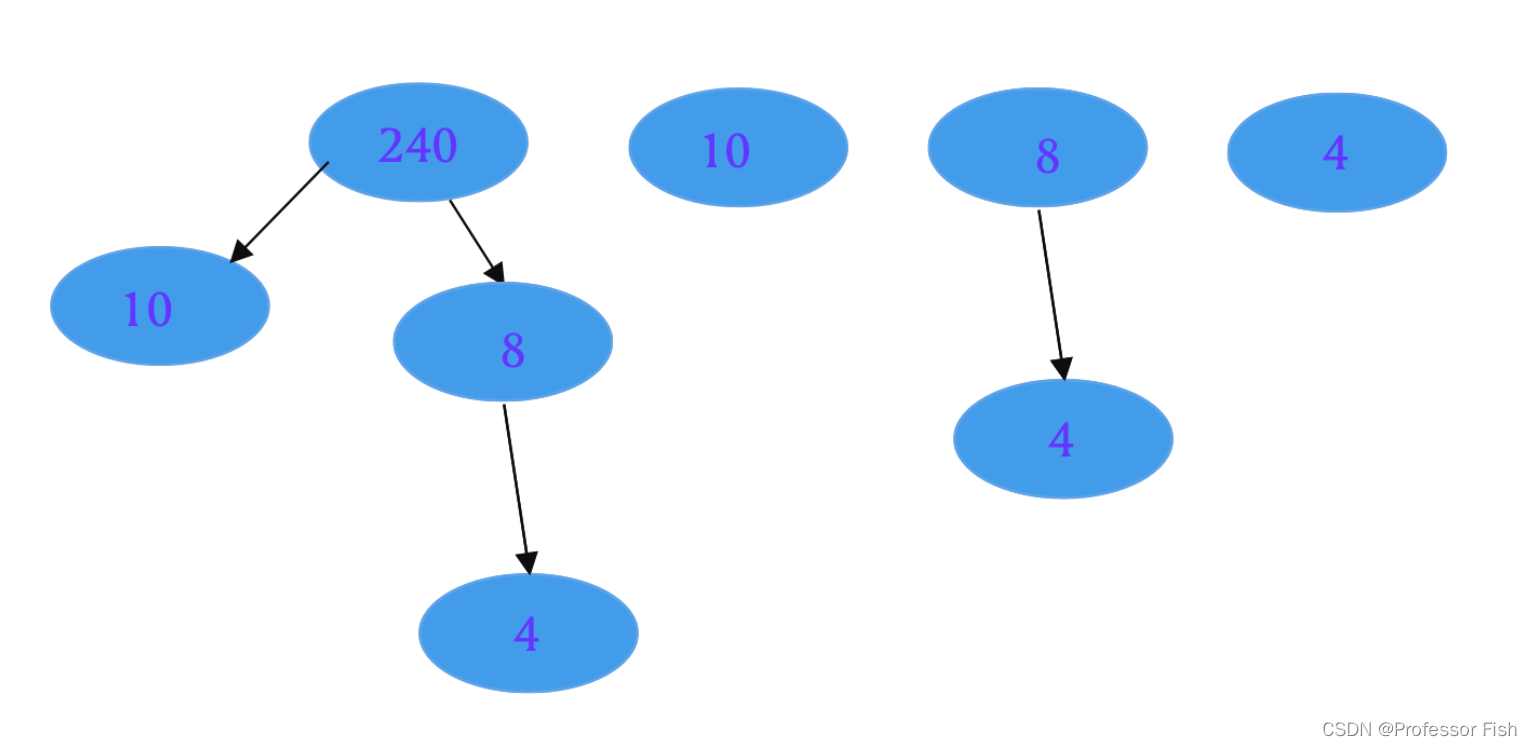
总结一下,到这里,以上所有的思路,都不会得到最终结果,因枚举到某个对象时,他可能的因数可能会跳过比当前数小的值,最长的可能是比之次小的因数,所以枚举一种的前提下是有可能由多种情况的,但是这个情况用暴力的方式很难解决,以**[4,8,10,240]**为例,会有以下枚举树,代码实现不确定的树形,不好实现,所有这种思路感觉也不可取
动态规划(dynamic programming)
Simplifying a complicated problem by breaking it down into simpler sub-problems
动态规划常常适用于分治和最优子结构性质的问题
动态规划与递归
动态规划和递归或者分治没有根本上的区别(关键看有无最优的子结构)
共性:找到重复子问题
差异性:动态规划是最优子结构,中途可以淘汰次优解
动态规划是自底向上,递归是自顶向下
啥叫「自顶向下」?
注意我们刚才画的递归树(或者说图),是从上向下延伸,都是从一个规模较大的原问题比如说 f(20),向下逐渐分解规模,直到 f(1) 和 f(2) 触底,然后逐层返回答案,这就叫「自顶向下」
func fibo(n int)int{
if n<=1{
return n
}
return fibo(n-1)+fibo(n-2)
}
啥叫「自底向上」?
反过来,我们直接从最底下,最简单,问题规模最小的 f(1) 和 f(2) 开始往上推,直到推到我们想要的答案 f(20),这就是动态规划的思路,这也是为什么动态规划一般都脱离了递归,而是由循环迭代完成计算。
func fibo(n int) int {
dp := make([]int, n+1)
dp[0] = 0
dp[1] = 1
for i := 2; i <= n; i++ {
dp[i] = dp[i-1] + dp[i-2]
}
return dp[n]
}
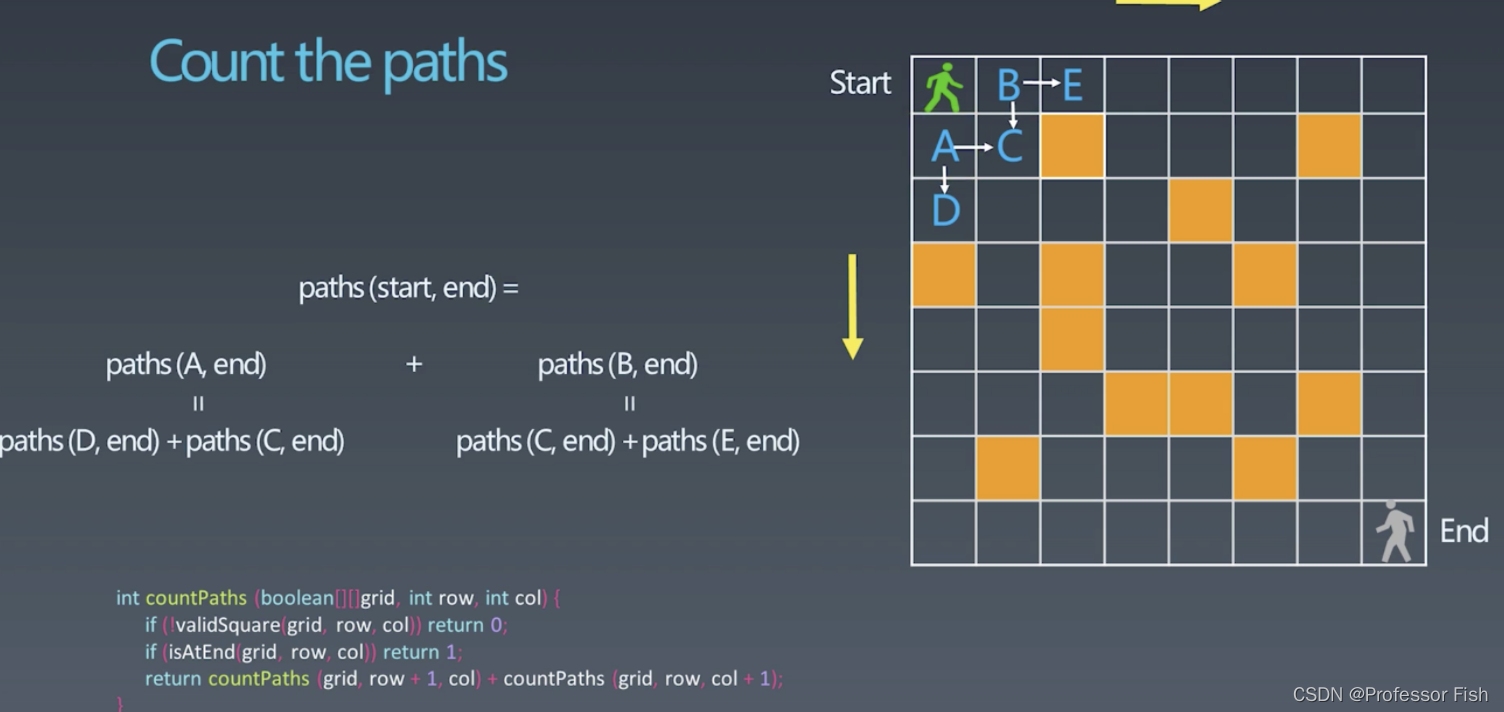
Count the paths
黄色框是障碍物,只能向右或者向下走,有多少种走法?
递归
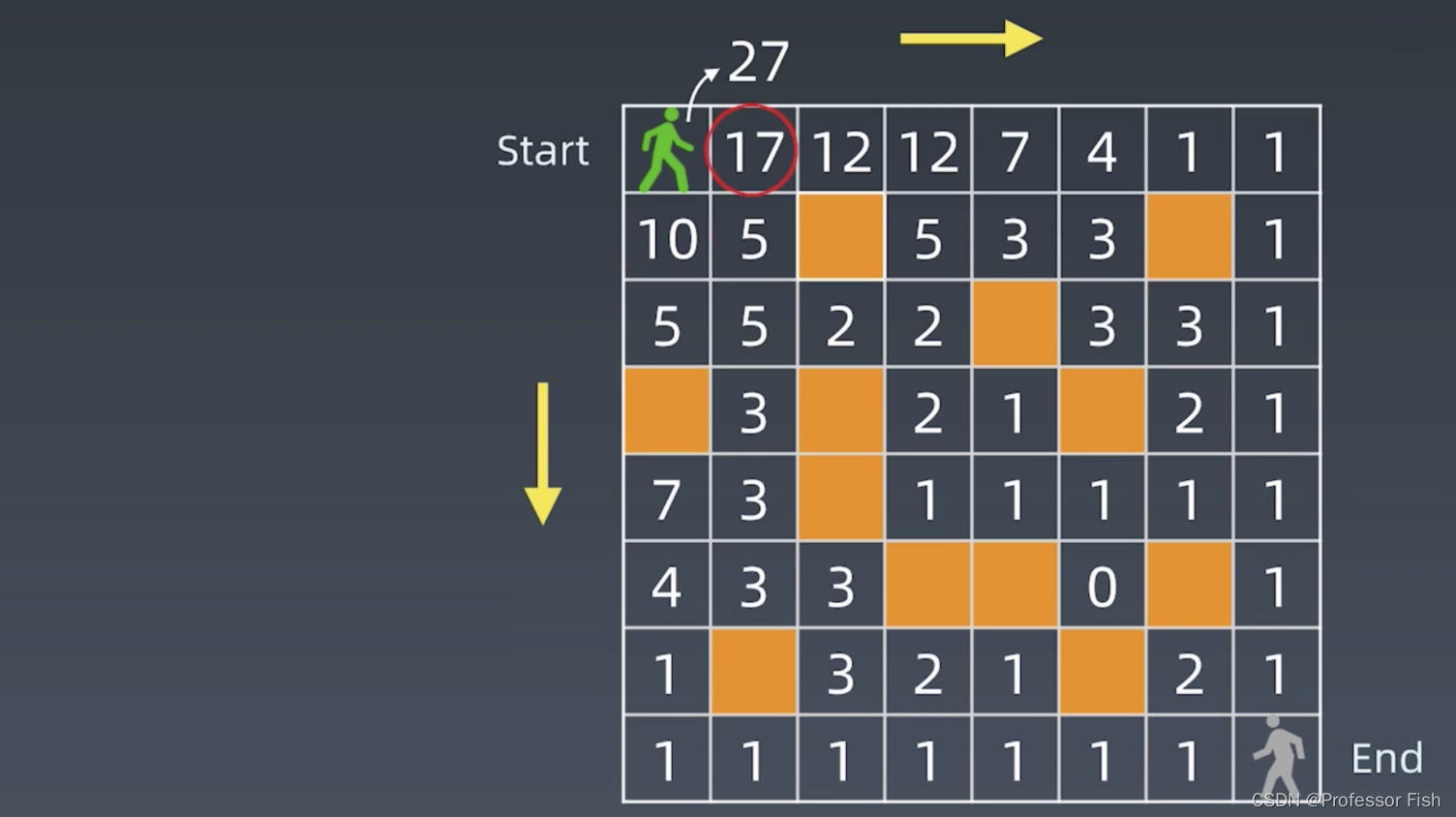
dp递推

dp递推结果

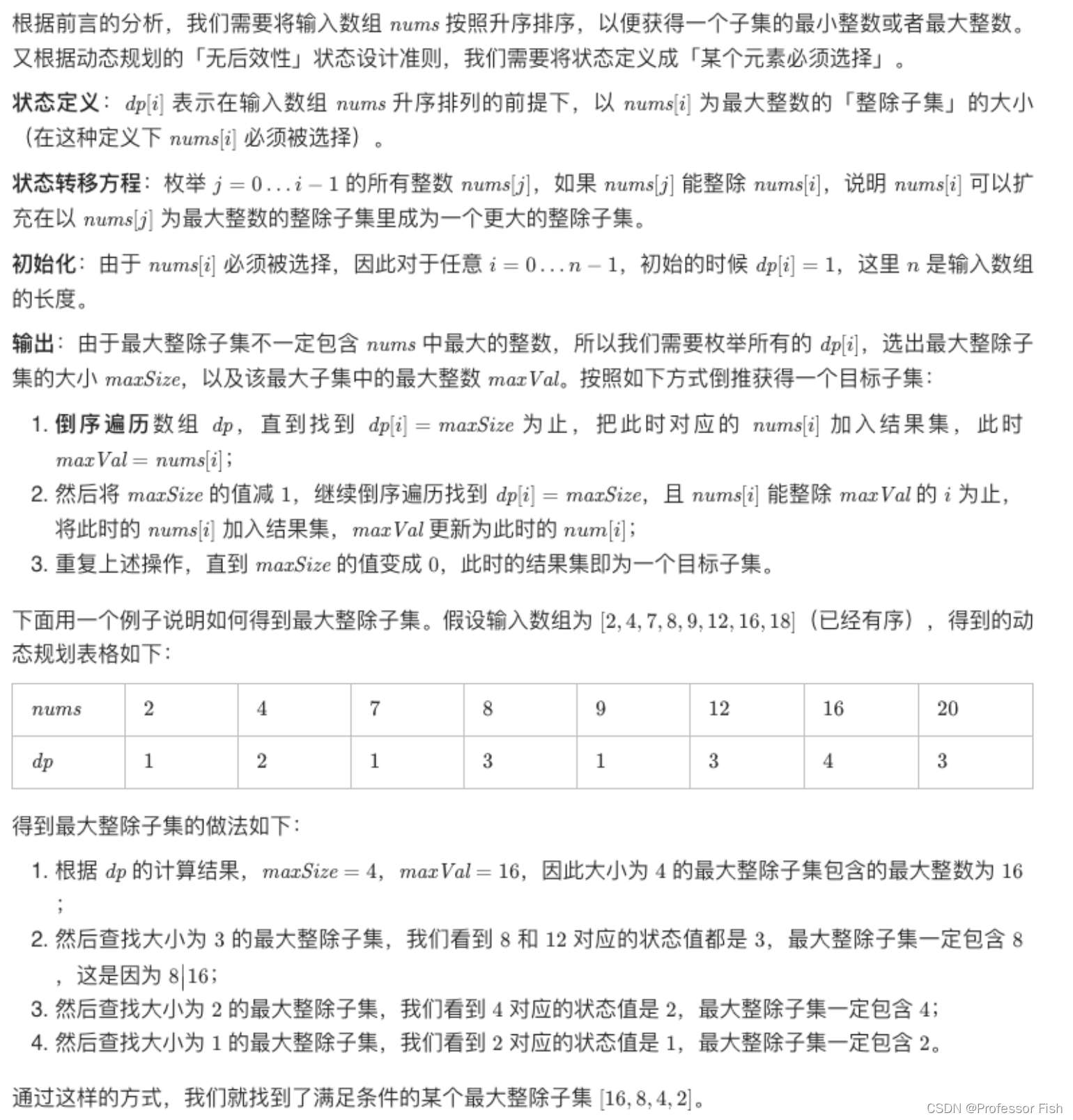
最终解答
func largestDivisibleSubset(nums []int) (res []int) {
sort.Ints(nums)
// 第 1 步:动态规划找出最大子集的个数、最大子集中的最大整数
n := len(nums)
dp := make([]int, n)
for i := range dp {
dp[i] = 1
}
maxSize, maxVal := 1, 1
for i := 1; i < n; i++ {
for j, v := range nums[:i] {
if nums[i]%v == 0 && dp[j]+1 > dp[i] {
dp[i] = dp[j] + 1
}
}
if dp[i] > maxSize {
maxSize, maxVal = dp[i], nums[i]
}
}
if maxSize == 1 {
return []int{nums[0]}
}
// 第 2 步:倒推获得最大子集
for i := n - 1; i >= 0 && maxSize > 0; i-- {
if dp[i] == maxSize && maxVal%nums[i] == 0 {
res = append(res, nums[i])
maxVal = nums[i]
maxSize--
}
}
return
}