目录
内部八大排序
冒泡排序、选择排序、直接插入排序、希尔排序、二路归并排序、快速排序、堆积排序、基数(桶)排序
排序是指将一组数据,按特定规则调换位置,是数据句有某种顺序关系(递增或递减)。
排序过程中,数据移动的方式可分为“直接移动”和“逻辑移动”两种;??
直接移动是直接交换存储数据的位置,逻辑移动不会移动数据存储的位置,仅仅改变指向数据的指针的值。
排序算法的评价:时间复杂度、空间复杂度、稳定性;
时间复杂度:时间复杂度是一个函数,它定性描述了该算法的运行时间。
空间复杂度:指算法在执行过程中需要占用的额外内存空间。
如何直观的判断稳定性:看算法中是否存在跳跃交换
冒泡排序:
时间复杂度O(n^2),? ?空间复杂度O(1),? ?稳定性:稳定
从第一个元素开始,比较相邻元素的大小,若大小顺序有误,则对调后再进行下一个元素的比较;
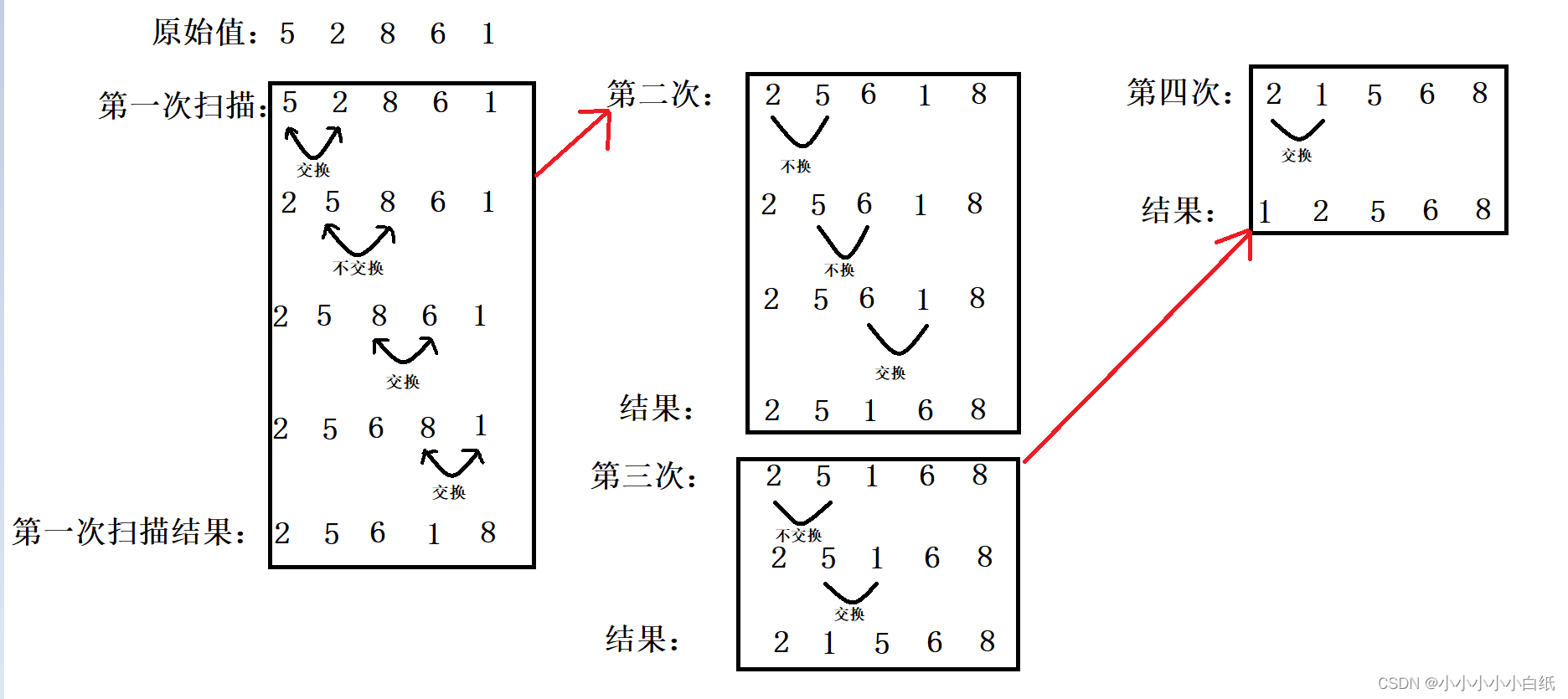
?第一次遍历保证最大值放到最后,第二次遍历保证除去最大值之外元素内的最大值放到最后...,每次遍历后的下一次遍历可以减少对最后一个元素的比较。
n个元素的冒泡排序需要进行n-1次的扫描
void BubbleSort(int arr[], int len)
{
bool tag = true;//优化标记 如果当前这轮存在一次交换 则tag变成FALSE
//当tag为true不就代表着不存在前面比后面大
//则已经完全有序 那直接退出即可 剩余轮次不需要执行
int count = 0;
for (int i = 0; i < len - 1; i++)//少一轮
{
tag = true;
for (int j = 0; j + 1 < len - i; j++)//j<len-1-i
{
if (arr[j] > arr[j + 1])//两两比较 前面大于后面 则交换两个值
{
tag = false;
int tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
}
}
count++;
if (tag)
{
break;
}
}
}选择排序
?时间复杂度O(n^2),? 空间复杂度O(1)? ,? 稳定性:不稳定
1.首先找到数列元素中的最小值与第一个元素交换
2.从第二个值开始找,找到数列中(不含第一个)的最小值,在和第二个值交换
3.从第三个值开始,找到数列中(不含第一、二个)的最小值,在和第三个值交换...
4.和前边步骤相同...............

void SelectSort(int* arr, int len)
{
int minindex; //最小值的下标
for (int i = 0; i < len - 1; i++)
{
minindex = i;//排序序列的第一个值是最小值 所以minindex为i
for (int j = i + 1; j < len; j++)//排序序列的第二个值开始和arr[minindex]比较
{
if (arr[j] < arr[minindex])//如果找到更小的数 则minindex重新赋值为新的最小值的下标
{
minindex = j;
}
}
//直接进行交换
if (i != minindex)
{
int tmp = arr[i];//因为i保存的是待排序序列第一个值
arr[i] = arr[minindex];
arr[minindex] = tmp;
}
}
}直接插入排序
?时间复杂度O(n^2), 空间复杂度O(1),稳定性:? 稳定
将数组中的元素逐一与排序好的数据进行比较,前两个元素先排好,再将第三个元素插入适当的位置,所以插入后仍然是排好序的,接着将第四个元素插入......重复此步骤,直至全部元素插入。

void InsertSort(int arr[], int len)
{
assert(arr != NULL);
if (arr == NULL)
{
return;
}
int count = 0;
int tmp;
int j;//将j的生存周期提高,保证break后的的代码arr[j+1] = tmp;有效
for (int i = 1; i < len; i++)//每次从待排序队列中取的值
{
tmp = arr[i];//用tmp保存待插入的值
for (j = i - 1; j >= 0; j--)//从右向左找不比tmp大的值
{
if (arr[j] > tmp)//如果比tmp大 则向右放一格
{
arr[j + 1] = arr[j];
count++;
}
else//如果不比tmp大
{
break;
}
}
arr[j + 1] = tmp;
}
}希尔排序
时间复杂度O(n^1.5) ,? 空间复杂度O(1), 稳定性:?不稳定
eg:6? 9? 2? 3? 4? 7? 5? 1
首先,将元素分成Y(8/2)=4,化分数不一定是2,素数最好。
(简单的来说是一个特殊的直接插入排序,相当于多次调用直接插入排序,每一次的增量保持互素,并且最后一个增量一定位1,为1才能保证其完全有序? ?)

void Shell(int arr[], int size)
{
int jump = size/2;//位移量
int tmp;//暂存数据
int i; //扫描次数
int j; //定位比较元素
int k = 1;
while(jump != 0)
{
for (int i = jump; i < size; i++)//每次从待排序队列中取的值
{
tmp = arr[i];//用tmp保存待插入的值
for (j = i - jump; j >= 0; j = j - jump)//从右向左找不比tmp大的值
{
if (arr[j] > tmp)//如果比tmp大 则向右放一格
{
arr[j + jump] = arr[j];
k++;
}
else//如果不比tmp大
{
break;
}
}
arr[j + gap] = tmp;
}
cout<<"第"<< k++ <<"次排序:";
showdata(data);
jump = jump / 2;
}
}合并排序
时间复杂度O(nlogn) , 空间复杂度O(nlogn), 稳定性:稳定
步骤:
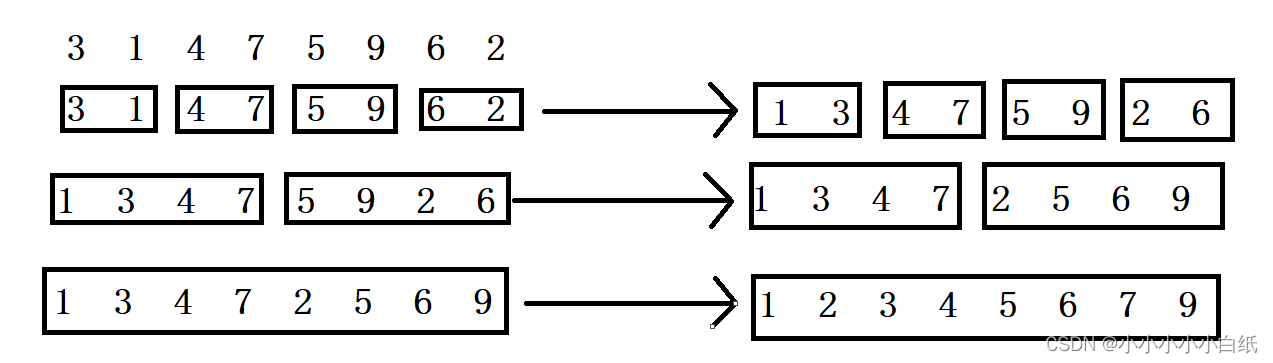
- 将N个长度为1的键值,成对的合并成N/2个长度为2的键值组
- 将N/2个长度为2的键值组,成对的合并成N/4个长度为4的键值组
- 将键值组不断合并,知道合并成一组长度为N的键值组为止
合并排序最大的好处是在数据呈现最坏的情况时,是所有排序法中最好的,属于二分切割法的稳定排序。
void Merge(int arr[], int len)
{
int* brr = (int*)malloc(sizeof(int) * len);//申请额外的辅助空间brr
assert(brr != NULL);
int gap = 1;
int low1 , high1 , low2 , high2 ,i;
for (;gap < len; gap *= 2)
{
low1 = 0;
high1 = low1 + gap - 1;
low2 = high1 + 1;
high2 = low2 + gap - 1 < len ? low2 + gap - 1 : len - 1;
i = 0;//i指向brr的下标
while (low2 < len)
{
while (low1 <= high1 && low2 <= high2)
{
if (arr[low1] <= arr[low2])
{
brr[i++] = arr[low1++];
}
else
{
brr[i++] = arr[low2++];
}
}
while (low1 <= high1)
{
brr[i++] = arr[low1++];
}
while (low2 <= high2)
{
brr[i++] = arr[low2++];
}
low1 = high2 + 1;
high1 = low1 + gap - 1;
low2 = high1 + 1;
high2 = low2 + gap - 1 < len ? low2 + gap - 1 : len - 1;
}
while (low1 < len)
{
brr[i++] = arr[low1++];
}
for (int i = 0; i < len; i++)
{
arr[i] = brr[i];
}
}
free(brr);
brr = NULL;
}
快速排序法
时间复杂度O(nlogn),? ?空间复杂度O(logn) ,稳定性: 不稳定
快速排序法又称分割交换排序法
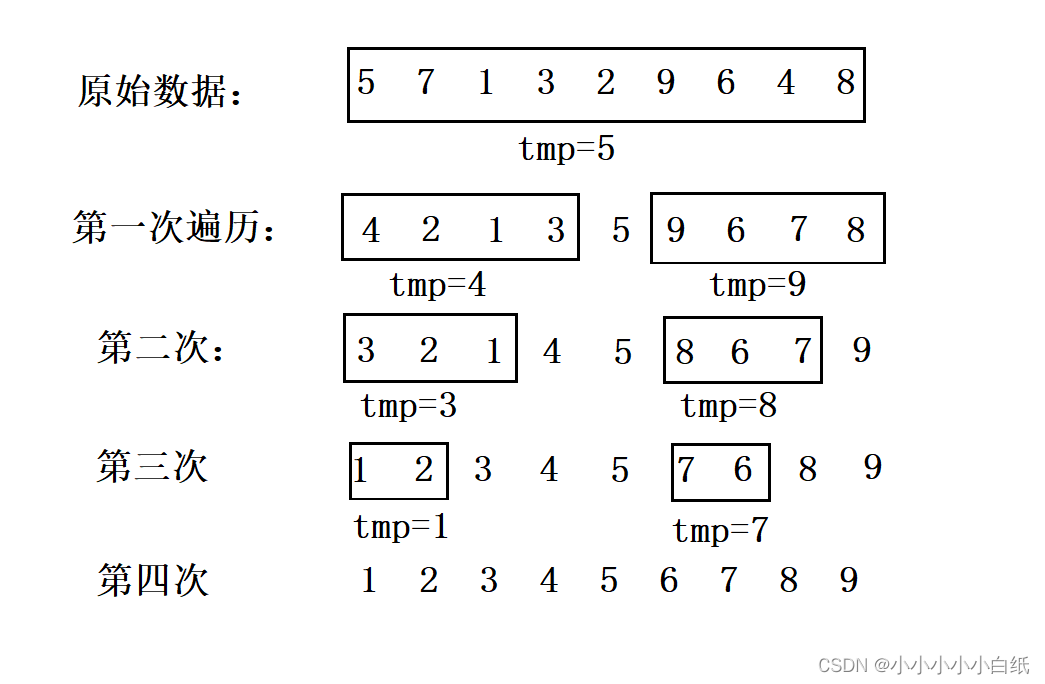
先会在数据中找到一个虚拟的中间值,并按照中间值将所有打算排序的数据分成两部分,其中小雨中间值的数据放在左边,大于中间值的数据放在右边,再以同样的放式分别处理左右两边的数据。
步骤:
- 先假设第一个键值K
- 从左向右找出键值Ki,使Ki > K
- 从右向左找出键值Kj,使Kj <K,
- 如果 i < j ,那么Ki与Kj互换,回到步骤2
- 如果 i >= j ,那么将 K 与 Kj 交换,并以 j 为基准点分割成左右两部分。再针对左右两边进行步骤1~5,知道左半边键值==右半边键值为止
?快速排序是平均运行最快的排序法,但是不稳定。
static int Partition(int* arr, int left, int right)
{
int tmp = arr[left];
while (left < right)
{
while (left<right && arr[right] > tmp)//从右向左找比tmp小的值 那如果比tmp大 则right-- 一下
right--;
if (left == right)//left == right 代表 找到了基准值该放的位置
{
break;
}
arr[left] = arr[right];//不然 就是找到了比tmp小的值 放到左侧即可
while (left < right && arr[left] <= tmp)//从左向右找比tmp大的值 那如果比tmp小 则left++ 一下
left++;
if (left == right)
{
break;
}
arr[right] = arr[left];//不然 就是找到了比tmp大的值 放到右侧即可
}
arr[left] = tmp;
return left;
}
static void Quick(int* arr, int left, int right)
{
if(left < right)
{
int par = Partition(arr, left, right);
Quick(arr, left, par-1);
Quick(arr, par+1, right);
}
}
void QuickSort(int arr[], int len)
{
Quick(arr, 0, len - 1);
}堆排序
时间复杂度O(nlogn), 空间复杂度O(1),稳定性:不稳定?
堆排序可以看作选择排序的改进版,它可以减少在选择排序中的比较次数,进而减少排序时间。
用到了二叉树的技巧,利用堆积树来完成排序的。堆积树是一个特殊的二叉树,分文最大堆积和最小堆积两种。
最大堆积:
- 是一个完全二叉树
- 所有的节点的值都大于或等于它左右子节点的值
- 树根是堆积树中最大的
最小堆积:
- ?是一个完全二叉树
- 所有的节点的值都小于或等于它左右子节点的值
- 树根是堆积树中最小的
?将二叉树转换成堆积树,用数组来存储二叉树所有节点的值。
eg:arr[0]=32,? arr[1]=17,??arr[2]=16,??arr[3]=24,??arr[4]=35? ,??arr[5]=?87 ,?arr[6]=65? ,?arr[7]=4,??arr[8]=12;
- arr[0]为根,若arr[1]大于父节点,则互换,小于则不互换。
- arr[1]<arr[0];? ?arr[2]<arr[0];??
- arr[3]>arr[1]-----互换? ?,arr[4]>arr[1]------互换,再与arr[0]比较,arr[1]>arr[0]----互换
- arr[5]>arr[2]----互换? , 再与arr[0]比较arr[2]>arr[0],互换
- arr[6]>arr[2]----互换, 再与arr[0]比较,arr[2]<arr[0]
- arr[7]<arr[3]? ?,? ?arr[8]<arr[3]??

依次将得到的树根节点(最大值)和最后一个叶子节点的值进行交换,并且交换后,最后的尾部节点不参与下一次调整。
最后得到排序的元素
//从最后一个非叶子节点开始向上查找
void HeapAdjust(int arr[], int start, int end)
{
int tmp = arr[start];
for (int i = start * 2 + 1; i <= end; i = start * 2 + 1)/
{
if (i < end && arr[i] < arr[i + 1])
{
i++;
}
if (arr[i] > tmp)
{
arr[start] = arr[i];
start = i;
}
else
{
break;
}
}
arr[start] = tmp;
}
void HeapSort(int arr[], int len)
{
for (int i = (len - 1 - 1) / 2; i >= 0; i--)//O(n)
{
HeapAdjust(arr, i, len - 1);//(logn)
}
//根节点和尾节点交换
for (int i = 0; i < len - 1; i++)//O(n)
{
int tmp = arr[0];
arr[0] = arr[len - 1 - i];//9 8 7 6 5 4 3 2 1
arr[len - 1 - i] = tmp;
HeapAdjust(arr, 0, (len - 1 - i) - 1);//(最后一个节点的下标再-1,最后一个节点不参与运算
}
}基数排序
分配模式排序。时间复杂度O(n logp k),? 空间复杂度O(n*p)? ,稳定性:稳定
p字符数、k数据的最大值
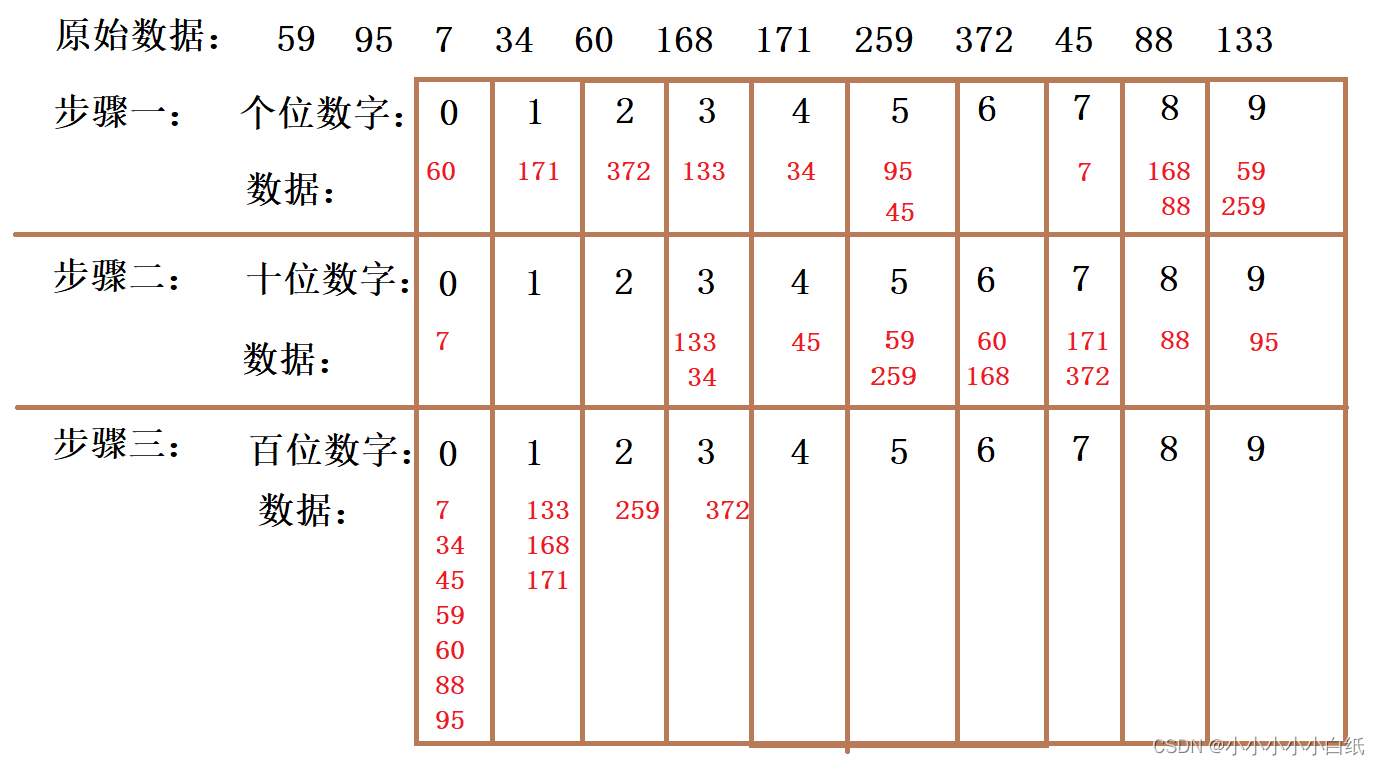
步骤:
- 把每个证书按其个位数字放到列表中,合并
- 按十位数字,按序放到列表中,合并
- 按百位数字,按序放到列表中,合并
void radix(int data[], int size)
{
for (int n = 1; n <= 100; n *= 10)//n为基数,从个位数开始排序
{
int tmp[10][100] = { 0 };//暂存数组,[0~9位数][数据个数]
for (int i = 0; i < size; ++i)
{
int n_num = (data[i] / n) % 10; //n_num是n位数的值
tmp[n_num][i] = data[i];//把data[i]的数据放到tmp里
}
int count = 0;
for (int i = 0; i < 10; ++i)
{
for (int j = 0; j < size; ++j)
{
if (tmp[i][j] != 0)
{
data[count] = tmp[i][j];//data暂存在tmp
count++;
}
}
}
}
}