[数据结构与算法]常见算法题分类总结之归并排序(Merge-Sort)：从二路到多路

前置知识

插入排序

1. 插入排序
   步骤：

1.从第一个元素开始，该元素可以认为已经被排序
2.取下一个元素tem，从已排序的元素序列从后往前扫描
3.如果该元素大于tem，则将该元素移到下一位
4.重复步骤3，直到找到已排序元素中小于等于tem的元素
5.tem插入到该元素的后面，如果已排序所有元素都大于tem，则将tem插入到下标为0的位置
6.重复步骤2~5

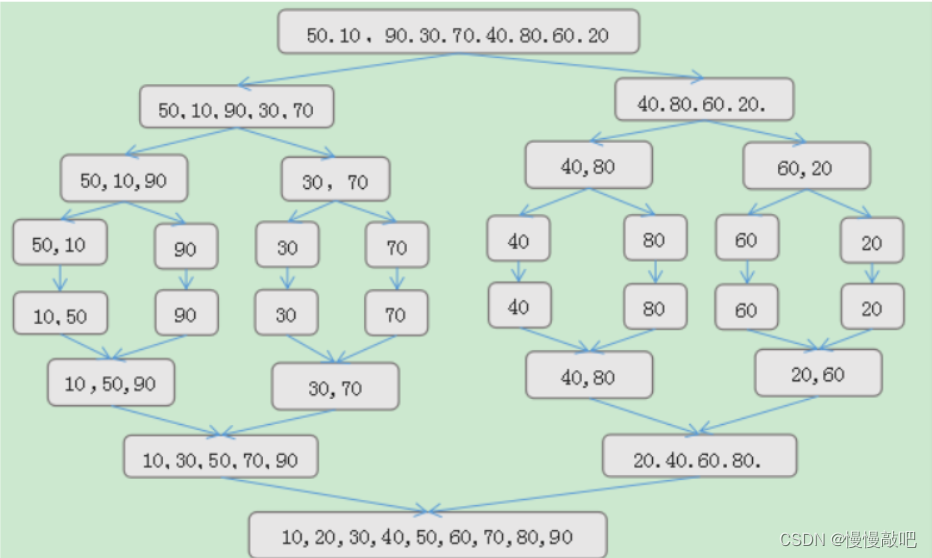
归并排序

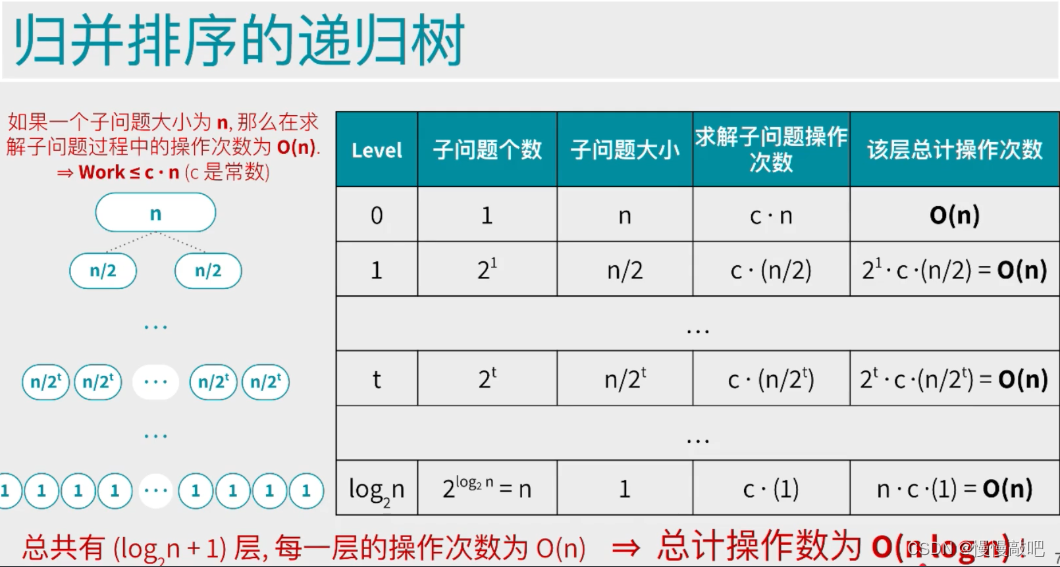
归并排序（Merge sort）是建立在归并操作上的一种有效的排序算法，归并排序对序列的元素进行逐层折半分组，然后从最小分组开始比较排序，合并成一个大的分组，逐层进行，最终所有的元素都是有序的
归并排序的核心：分治

归并排序与插入排序对比

基础的二路归并(c++)

//基础的二路归并
//核心思想：划分为两个子问题
//左边处理一下，得到左边的信息
//右边处理一下，得到右边的信息
//最后再处理一下，横跨左右两边的信息
void merge_sort(int *arr, int l, int r){
    if(l >= r) return;
    int mid = (l + r) / 2;
    
    cout << endl;
    cout << "sort : " << l << "<--->" << r << " : " << endl;
    for(int i = l; i <= r; i++){
        cout << arr[i] << " ";
    }
    cout << endl; //换行
    //上面几行用来打印 方便观察
    
    merge_sort(arr, l, mid);
    merge_sort(mid + 1, r);
    vector<int> temp(r - l + 1);
    int k = 0, p1 = l, p2 = mid + 1;
    //当左右两个区间还有元素的时候
    while(p1 <= mid || p2 <= r){
        //1. 右区间为空
        //2. 左区间没空，并且，左区间的元素比较小
        if((p2 > r) || (p1 <= mid && arr[p1] <= arr[p2])){
            temp[k] = arr[p1];//最开始是把p1指向元素放进temp 0下标中
            k++, p1++;
        }else{//左区间空了，把右区间元素放进去
            temp[k] = arr[p2];
            k++, p2++;
        }
    }//右区间还有元素的话，继续把右区间的元素放进去
    for(int i = l; i <= r; i++){
        arr[i] = temp[i - l];
    }//上面那两行相当于覆盖操作
    
    //打印
    for(int i = l; i <= r; i++){
        cout << arr[i] << " ";
    }
    cout << arr[i] << " ";
    return ;
}

int main(){
    int a[10] = {1, 9, 0, 2, 5, 6, 2, 7, 1, 9};
    merge_sort(a, 0, 9);
    for(int i = 0; i < 10; i++){
        cout << a[i] << " ";
    }
    return 0;
}
//归并排序稳定 时间复杂度：O(nlogn) 
//空间复杂度：那个临时数组是在函数内部开辟的空间，属于栈上开辟的变量，先开辟n/2后再释放n/2，再开辟n/2，再释放... 最大的情况是开辟n的，所以空间复杂度为 O(n)

问题：电脑内存大小2GB，如何对一个40GB的文件进行排序？

1. 分成20个数组，每个处理2GB的文件，最终得到20个有序数组
2. 对文件的写入支持追加写，所以不需要临时变量来存
3. 我们可以借助小顶堆加速，比如对20行文件以流的方式只读第一行文件
4. 得到最小的文件后在后面继续追加，一直重复这个过程
5. 时间复杂度：O(nlogn) * 20 + O(1) + O(n) O(1)因为堆是常量空间 O(n) 是扫一行 然后O(1)可以忽略掉，所以最后时间复杂度为：O(nlogn + n)

//插入排序：
/*
 * 插入排序算法：
 * 1、以数组的某一位作为分隔位，比如index=1，假设左面的都是有序的.
 * 
 * 2、将index位的数据拿出来，放到临时变量里，这时index位置就空出来了.
 * 
 * 3、从leftindex=index-1开始将左面的数据与当前index位的数据（即temp）进行比较，如果array[leftindex]>temp,
 * 则将array[leftindex]后移一位，即array[leftindex+1]=array[leftindex],此时leftindex就空出来了.
 * 
 * 4、再用index-2(即leftindex=leftindex-1)位的数据和temp比，重复步骤3，
 * 直到找到<=temp的数据或者比到了最左面（说明temp最小），停止比较，将temp放在当前空的位置上.
 * 
 * 5、index向后挪1，即index=index+1，temp=array[index],重复步骤2-4，直到index=array.length,排序结束，
 * 此时数组中的数据即为从小到大的顺序.
 * 
 */
public class InsertSort {
    private int[] array;
    private int length;
    
    public InsertSort(int[] array){
        this.array = array;
        this.length = array.length;
    }
    
    public void display(){        
        for(int a: array){
            System.out.print(a+" ");
        }
        System.out.println();
    }
    
    /*
     * 插入排序方法
     */
    public void doInsertSort(){
        for(int index = 1; index<length; index++){//外层向右的index，即作为比较对象的数据的index
            int temp = array[index];//用作比较的数据
            int leftindex = index-1;
            while(leftindex>=0 && array[leftindex]>temp){//当比到最左边或者遇到比temp小的数据时，结束循环
                array[leftindex+1] = array[leftindex];
                leftindex--;
            }
            array[leftindex+1] = temp;//把temp放到空位上
        }
    }
    
    public static void main(String[] args){
        int[] array = {38,65,97,76,13,27,49};
        InsertSort is = new InsertSort(array);
        System.out.println("排序前的数据为：");
        is.display();
        is.doInsertSort();
        System.out.println("排序后的数据为：");
        is.display();
    }
}


//归并排序：
public class MergeSort {
    //两路归并算法，两个排好序的子序列合并为一个子序列
    public void merge(int[] a,int left,int mid,int right){
        int[] tmp=new int[a.length];//辅助数组
        int p1=left,p2=mid+1,k=left;//p1、p2是检测指针，k是存放指针
        while(p1<=mid && p2<=right){
            if(a[p1]<=a[p2])
                tmp[k++]=a[p1++];
            else
                tmp[k++]=a[p2++];
        }

        while(p1<=mid) tmp[k++]=a[p1++];//如果第一个序列未检测完，直接将后面所有元素加到合并的序列中
        while(p2<=right) tmp[k++]=a[p2++];//同上

        //复制回原数组
        for (int i = left; i <=right; i++) 
            a[i]=tmp[i];
    }

    public void mergeSort(int[] a,int start,int end){
        if(start<end){//当子序列中只有一个元素时结束递归
            int mid=(start+end)/2;//划分子序列
            mergeSort(a, start, mid);//对左侧子序列进行递归排序
            mergeSort(a, mid+1, end);//对右侧子序列进行递归排序
            merge(a, start, mid, end);//合并
        }
    }

    @Test
    public void test(){
        int[] a = { 49, 38, 65, 97, 76, 13, 27, 50 };
        mergeSort(a, 0, a.length-1);
        System.out.println("排好序的数组：");
        for (int e : a)
            System.out.print(e+" ");
    }
}

经典题目

开胃菜

//力扣题：21 88 56
//21
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
        if(list1 == null){
            return list2;
        }else if(list2 == null){
            return list1;
        } else if (list1.val < list2.val) {
            list1.next = mergeTwoLists(list1.next, list2);
            return list1;
        } else {
            list2.next = mergeTwoLists(list1, list2.next);
            return list2;
        }
    }
    //虚拟头节点+迭代方法
    public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
        ListNode hair = new ListNode(-1);
        ListNode pre = hair;
        while(list1 != null && list2 != null){
            if(list1.val <= list2.val){
                pre.next  = list1;
                list1 = list1.next;
            }else{
                pre.next = list2;
                list2 = list2.next;
            }
            //继续往后迭代
            pre = pre.next;
        }
        // 合并后 l1 和 l2 最多只有一个还未被合并完，我们直接将链表末尾指向未合并完的链表即可
        pre.next = list1 == null ? list2 : list1;
        return hair.next;
    }
}

/*复杂度分析
时间复杂度：O(n + m)，其中 n 和 m 分别为两个链表的长度。因为每次调用递归都会去掉 l1 或者 l2 的头节点（直到至少有一个链表为空），函数 mergeTwoList 至多只会递归调用每个节点一次。因此，时间复杂度取决于合并后的链表长度，即 O(n+m)。
空间复杂度：O(n + m)，其中 n 和 m 分别为两个链表的长度。递归调用 mergeTwoLists 函数时需要消耗栈空间，栈空间的大小取决于递归调用的深度。结束递归调用时 mergeTwoLists 函数最多调用 n+m 次，因此空间复杂度为 O(n+m)
*/  

/*Java中arraycopy方法
System.arraycopy(src, srcPos, dest, destPos, length);
src表示源数组
srcPos表示源数组中拷贝元素的起始位置。
dest表示目标数组
destPos表示拷贝到目标数组的起始位置
length表示拷贝元素的个数*/

//需要注意的是在进行数组拷贝时，目标数组必须有足够的空间来存放拷贝的元素，否则就会发生角标越界异常。
//    ！！！！另外还需要注意的是目标数组相对应位置上的元素会被覆盖掉
    
//88 合并两个有序数组
    class Solution {
    public void merge(int[] nums1, int m, int[] nums2, int n) {
            int p1 = m-1;
            int p2 = n-1;
            int p = m+n-1;

            while((p1>=0) && (p2>=0))
                nums1[p--] = (nums1[p1]<nums2[p2]) ? nums2[p2--] : nums1[p1--];
                System.arraycopy(nums2,0,nums1,0,p2+1);  
                
    }
}
//时间复杂度：O(m+n)。
//指针移动单调递减，最多移动 m+n 次，因此时间复杂度为 O(m+n)
//空间复杂度：O(1)
//直接对数组nums1原地修改，不需要额外空间

//56 合并区间
//以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回 一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间 

class Solution {
    //思路:区间只有三种情况：包含、相交、独立 我们合并前两种
	//对区间起始位置从小到大排序 A[] B[] A[尾] >= B[头] 就合并
	public int[][] merge(int[][] intervals) {
		Arrays.sort(intervals, new Comparator<int[]>() {//排序
			@Override
			public int compare(int[] o1, int[] o2) {
				return o1[0] - o2[0];
			}
		});
		int[][] res = new int[intervals.length][2];//结果集数组
		int ind = -1;//索引 告诉我们合并的集合应该放在结果集的哪个位置
		for(int[] interval : intervals) {
			//说明是我们第一个拿到的区间 或者 当前数组头部大于上次拿到数组的尾部
			if(ind == -1 || interval[0] > res[ind][1]) {
				res[++ind] = interval;
			}else {//此时相交或者包含 确定边界
				res[ind][1] = Math.max(res[ind][1], interval[1]);
			}
		}//走到这里后面要切割无用部分
		return Arrays.copyOf(res, ind + 1);
    }
}    

剑指offer51.数组中的逆序对(hard)

/**
 * 剑指offer51.数组中的逆序对(困难)
 * @author: William
 * @time:2022-05-09
 */
public class Num51 {
	public int reversePairs(int[] nums) {
		if(nums.length < 2) return 0;
		return merge_sort(nums, 0, nums.length - 1);
	}
	
	private int merge_sort(int[] nums, int L, int R) {
		if(L >= R) return 0;
		int mid = L + ((R - L) >> 1), ans = 0;
		//分治 两个数组都是递增的，p1都比p2大，那p1后面的数更加比p2大
		ans = merge_sort(nums, L, mid) + merge_sort(nums, mid + 1, R);
		//归并
		int[] tmp = new int[R - L + 1];
		int k = 0, p1 = L, p2 = mid + 1;
		while(p1 <= mid || p2 <= R) {
			if((p2 > R) || (p1 <= mid && nums[p1] <= nums[p2])) {
				tmp[k++] = nums[p1++];
			}else {
				//只有p1 > p2 的情况下才走到这 是逆序对
				tmp[k++] = nums[p2++];
				ans += (mid - p1 + 1);
			}
		}//将数组元素放到原数组中
		for(int i = 0; i < tmp.length; i++) nums[i + L] = tmp[i];
		return ans;
	}
	//k神版本
	int[] nums, temp;
	public int reversePairs1(int[] nums) {
		this.nums = nums;
		temp = new int[nums.length];
		return mergeSort(0, nums.length - 1);
	}
	private int mergeSort(int L, int R) {
		//终止条件
		if(L >= R) return 0;
		//递归划分
		int m = (L + R) >> 1;
		int res = mergeSort(L, m) + mergeSort(m + L, R);
		//合并阶段
		int i = L, j = m + 1;
		for(int k = L; k <= R; k++) {
			temp[k] = nums[k];
		}
		for(int k = L; k <= R; k++) {
			if(i == m + 1)
				nums[k] = temp[j++];
			else if(j == R + 1 || temp[i] <= temp[j])
				nums[k] = temp[i++];
			else {
				nums[k] = temp[j++];
				res += m - i + 1;//统计逆序对
			}
		}
		return res;
	}
}

合并K个升序链表(hard)

/**
 * 合并K个升序链表(困难)
 * @author: William
 * @time:2022-05-09
 */
class ListNode {
     int val;
     ListNode next;
     ListNode() {}
     ListNode(int val) { this.val = val; }
     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
}

public class Num23 {
	//小顶堆
	public ListNode mergeKLists(ListNode[] lists) {
		if (lists == null || lists.length == 0) return null;
		PriorityQueue<ListNode> q = new PriorityQueue<ListNode>(new Comparator<ListNode>() {
			@Override
			public int compare(ListNode o1, ListNode o2) {
				return o1.val - o2.val;
			}
		});//把链表中的数据塞到小顶堆中
		for(ListNode list : lists) if(list != null) q.offer(list);		
		//新的链表来存储合并后的结果集 并且从虚拟头节点开始
		ListNode ret = new ListNode(-1), p = ret;
		while(!q.isEmpty()) {
			ListNode cur = q.poll();
			p.next = cur;//继续往后迭代
			p = cur;
			if(cur.next != null) q.offer(cur.next);
		}
		return ret.next;
    }	
}

排序链表

/**
 * 排序链表
 * @author: William
 * @time:2022-05-09
 */
public class Num148 {
	public ListNode sortList(ListNode head) {
		int n = 0;
		ListNode p = head;
		while(p != null) {
			p = p.next;
			n++;
		}//得到链表的长度
		return merge_sort(head, n);
    }
	private ListNode merge_sort(ListNode head, int n) {
		if(n <= 1) return head;
		int l_cnt = n >> 1, r_cnt = n - l_cnt;
		ListNode ret = new ListNode(-1), L = head, R = L, p = L;
		for(int i = 0; i < l_cnt - 1; i++) p = p.next;//p此时走到左边链表的尾部
		R = p.next;
		p.next = null;//此时完成左右链表的拆分
		//开始合并
		L = merge_sort(L, l_cnt);
		R = merge_sort(R, r_cnt);
		p = ret;
		while(L != null || R != null) {
			if((R == null) || (L != null && L.val <= R.val)) {
				p.next = L;
				p = L;
				L = L.next;
			}else {
				p.next = R;
				p = R;
				R = R.next;
			}
		}
		return ret.next;
	}	
}

两根搜索树中的所有元素

/**
 * 两根搜索树中的所有元素
 * @author: William
 * @time:2022-05-10
 */
class TreeNode {
     int val;
     TreeNode left;
     TreeNode right;
     TreeNode() {}
     TreeNode(int val) { this.val = val; }
     TreeNode(int val, TreeNode left, TreeNode right) {
         this.val = val;
         this.left = left;
         this.right = right;
     }
}

public class Num1305 {
	//二叉搜索树在进行中序遍历的时候是递增的
	public List<Integer> getAllElements(TreeNode root1, TreeNode root2){
		List<Integer> list1 = new ArrayList<>();
		List<Integer> list2 = new ArrayList<>();
		List<Integer> res = new ArrayList<>();
		//得到两个递增集合
		inorder(root1, list1);
		inorder(root2, list2);
		int L = 0, R = 0;
		while(L < list1.size() || R < list2.size()) {
			if( (R >= list2.size()) || (L < list1.size() && list1.get(L) <= list2.get(R) )){
				res.add(list1.get(L++));
			}else {
				res.add(list2.get(R++));
			}
		}
		return res;
	}
	
	public void inorder(TreeNode root, List<Integer> list) {
		if(root == null) return;
		inorder(root.left, list);
		list.add(root.val);
		inorder(root.right, list);
	}
	
	//直接调用集合工具类哈哈哈
	List<Integer> ans;
    public List<Integer> getAllElements1(TreeNode root1, TreeNode root2) {
        ans = new ArrayList<>();
        dfs(root1);
        dfs(root2);
        Collections.sort(ans);
        return ans;
    }

    void dfs(TreeNode root) {
        if (root == null) return;
        dfs(root.left);
        ans.add(root.val);
        dfs(root.right);
    }
}

区间和的个数(hard)

/**
 * 区间和的个数(困难)
 * @author: William
 * @time:2022-05-11
 */
public class Num327 {
	//通过前缀和求区间和
	//low <= sum[j] - sum[i] <= upper
	int lower, upper;
	public int countRangeSum(int[] nums, int lower, int upper) {
		//初始化
		this.lower = lower;
		this.upper = upper;
		long[] sum = new long[nums.length + 1];
		sum[0] = 0;//求前缀和
		for(int i = 0; i < nums.length; i++) sum[i + 1] = sum[i] + nums[i];
		return merge_sort(sum, 0, sum.length - 1);
    }
	
	private int merge_sort(long[] nums, int L, int R) {
		if(L >= R) return 0;
		int mid = L + ((R - L) >> 1);
		int ans = 0;
		ans += merge_sort(nums, L, mid);
		ans += merge_sort(nums, mid + 1, R);
		ans += countTwoPart(nums, L, mid, mid + 1, R, lower, upper);
		int k = 0, p1 = L, p2 = mid + 1;
		long[] tmp = new long[R - L + 1];
		while(p1 <= mid || p2 <= R) {
			if((p2 > R) || (p1 <= mid && nums[p1] <= nums[p2])) {
				tmp[k++] = nums[p1++];
			}else {
				tmp[k++] = nums[p2++];
			}
		}
		for(int i = 0; i < tmp.length; i++) nums[i + L] = tmp[i];
		return ans;
	}
	//在并的过程中看有多少个元素符合条件
	private int countTwoPart(long[] nums, int l1, int r1, int l2, int r2, int lower, int upper) {
		int ans = 0;//记录多少个区间符合状态
		//j是右侧区间固定数 左侧查找范围
		for(int j = l2, k1 = l1, k2 = l1; j <= r2; j++) {
			//lower <= j-i <= upper	->	j - lower i >= i >= j - upper
			long a = nums[j] - upper;
			long b = nums[j] - lower;//确定两个边界
			while(k1 <= r1 && nums[k1] < a) k1++;//找到第一个边界就停
			//k2找比较大的边界 大于等于b的话说明站在最后一个的后面 等于也不要停 往后站一位
			while(k2 <= r1 && nums[k2] <= b) k2++;
			ans += k2 - k1;
		}
		return ans;
	}
}

计算右侧小于当前元素的个数(hard)

/**
 * 计算右侧小于当前元素的个数(困难)
 * @author: William
 * @time:2022-05-11
 */
public class Num315 {
	class Data{//每一个data的cnt记录右侧有多少元素小于当前元素
		int ind, val, cnt;
		
		public Data(int ind, int val) {
			this.ind = ind;
			this.val = val;
			this.cnt = 0;
		}
	}
	
	public List<Integer> countSmaller(int[] nums) {
		Data[] data = new Data[nums.length];
		for(int i = 0; i < nums.length; i ++) {
			data[i] = new Data(i, nums[i]);//把集合数据塞进去
		}
		merge_sort(data, 0, data.length - 1);
		Arrays.sort(data, new Comparator<Data>() {//下标从小到大排序
			@Override
			public int compare(Data o1, Data o2) {
				return o1.ind - o2.ind;
			}
		});
		List<Integer> res = new ArrayList<>();
		for(Data datum : data) {
			res.add(datum.cnt);//加入到结果集中
		}
		return res;
    }
	private void merge_sort(Data[] data, int L, int R) {
		if(L >= R) return;
		int mid = (L + R) >> 1;
		merge_sort(data, L, mid);
		merge_sort(data, mid + 1, R);
		//合并过程
		int k = 0, p1 = L, p2 = mid + 1;
		Data[] tmp = new Data[R - L + 1];
		while(p1 <= mid || p2 <= R) {//两边任意一个有值就可以
			if((p2 > R) || (p1 <= mid && data[p1].val > data[p2].val)) {
				//在前面找到一个比后面大的元素 开始计数
				data[p1].cnt += (R - p2 + 1);
				tmp[k++] = data[p1++];
			}else {//右侧小于左侧的情况
				tmp[k++] = data[p2++];
			}
		}
		for(int i = 0; i < tmp.length; i++) {
			data[i + L] = tmp[i];//将tmp数组中数据覆盖到data中
		}
	}
}

首个共同祖先

/**
 * 首个共同祖先
 * @author: William
 * @time:2022-05-11
 */
public class Num0408 {
	public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
		if(root == null) return null;
		if(root == p || root == q) return root;//至少找到一个
		TreeNode L = lowestCommonAncestor(root.left, p, q);
		TreeNode R = lowestCommonAncestor(root.right, p, q);
		if(L != null && R != null) return root;//p q都找到
		if(L != null && R == null) return L;//左边是找到的
		return R;
    }
}

层数最深叶子节点的和

/**
 * 层数最深叶子节点的和
 * @author: William
 * @time:2022-05-11
 */
public class Num1302 {
	int ans, max_k;
	
	public int deepestLeavesSum(TreeNode root) {
		ans = 0;
		max_k = 0;
		getAns(root, 0);
		return ans;
    }
	
	private void getAns(TreeNode root, int k) {
		if(root == null) return;
		if(k == max_k) ans += root.val;//当前叶子节点到了最深层 
		else if(k > max_k) {//达到新的最深层，前面的作废
			max_k = k;
			ans = root.val;
		}//继续向下递归
		getAns(root.left, k + 1);
		getAns(root.right, k + 1);
	}
}