[数据结构与算法]单调队列 → 常用于动态规划问题的优化

【算法解析】
单调队列是指在队尾入队出队，在队首出队，且其元素具有单调性的特殊队列。其中，在队尾入队出队的操作是用来维护单调队列的单调性，在队首出队的操作是用来维护单调队列的大小。单调队列常用于动态规划问题的优化。

在实践中，单调队列或者用数组模拟实现，或者用STL中的deque实现，不能用STL中的queue实现。

特别注意，单调队列里存放的是原始序列的元素下标，而不是元素值。这是因为我们无法用元素值来判断元素是否过期。但是，我们在下文中谈论元素大小时，指的不是原始序列的元素下标的大小，而是元素下标在原始序列中对应的元素值的大小。

单调队列求最值时的进出队规则，可助记如下：
★?构建单调递减队列的目的在于求最大值，求最大值时的操作为“大覆盖，小附加”（即：原始序列的待操作的元素，若比单调队列的队尾元素大，则按从单调队列的队尾元素向队首元素的方向，依序覆盖掉所有比原始序列的待操作的元素小的元素，直至遇到比原始序列的待操作的元素大的元素后终止；原始序列的待操作的元素，若比单调队列的队尾元素小，则附加到单调队列的队尾元素后面成为新的队尾元素）
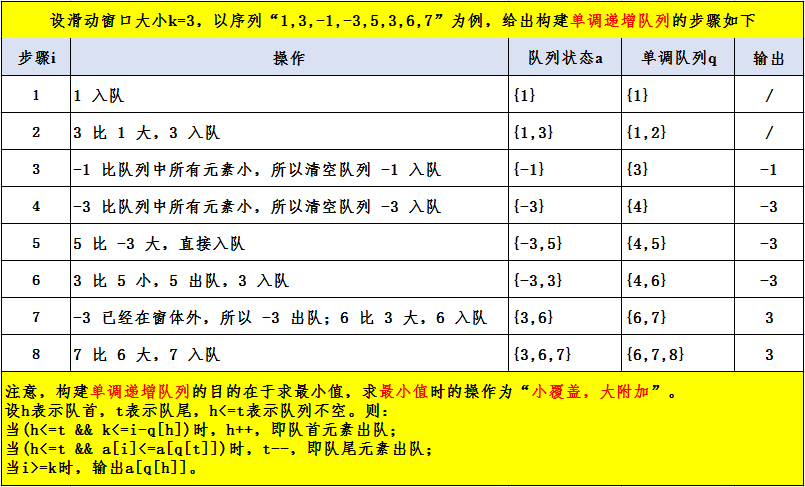
★?构建单调递增队列的目的在于求最小值，求最小值时的操作为“小覆盖，大附加”（即：原始序列的待操作的元素，若比单调队列的队尾元素小，则按从单调队列的队尾元素向队首元素的方向，依序覆盖掉所有比原始序列的待操作的元素大的元素，直至遇到比原始序列的待操作的元素小的元素后终止；原始序列的待操作的元素，若比单调队列的队尾元素大，则附加到单调队列的队尾元素后面成为新的队尾元素）

滑动窗口求最值问题，是单调队列的一个典型实践，它在基于队列优化的多重背包问题中有应用。题目来源于：
https://www.acwing.com/problem/content/156/
https://www.luogu.com.cn/problem/P1886

若给定滑动窗口大小为3，原始序列为{1, 3, -1, -3, 5, 3, 6, 7}，则滑动窗口求最值问题利用单调队列模拟的执行过程如下图所示：

?

【算法代码一】

#include <bits/stdc++.h>
using namespace std;
 
const int maxn=1000005;
int q1[maxn],q2[maxn];
int a[maxn];
int n,k;
 
void minque() {
	int h=1,t=0;
	for(int i=1; i<=n; i++) {
		while(h<=t && k<=i-q1[h]) h++;
		while(h<=t && a[i]<=a[q1[t]]) t--;
		q1[++t]=i;
		if(i>=k) {
			printf("%d ",a[q1[h]]);
		}
	}
}
 
void maxque() {
	int h=1,t=0;
	for(int i=1; i<=n; i++) {
		while(h<=t && k<=i-q2[h]) h++;
		while(h<=t && a[i]>=a[q2[t]]) t--;
		q2[++t]=i;
		if(i>=k) {
			printf("%d ",a[q2[h]]);
		}
	}
}
 
int main() {
	scanf("%d%d",&n,&k);
	for(int i=1; i<=n; i++) {
		scanf("%d",&a[i]);
	}
 
	minque();
	cout<<endl;
	maxque();
 
	return 0;
}
 
 
/*
in：
8 3
1 3 -1 -3 5 3 6 7
out：
-1 -3 -3 -3 3 3
3 3 5 5 6 7
*/

【算法代码二】

#include <bits/stdc++.h>
using namespace std;
 
const int maxn=1000005;
int a[maxn];
deque<int> q; //q存放编号
int n,k;
 
void que_min() {
	q.clear();
	for(int i=1; i<=n; i++){
		while(!q.empty() && i-k>=q.front()) q.pop_front();
		while(!q.empty() && a[i]<=a[q.back()]) q.pop_back();
		q.push_back(i);		
		if(i>=k) cout<<a[q.front()]<<" ";
	}
}
 
void que_max() {
	q.clear();
	for(int i=1; i<=n; i++){
		while(!q.empty() && i-k>=q.front()) q.pop_front();
		while(!q.empty() && a[i]>=a[q.back()]) q.pop_back();
		q.push_back(i);		
		if(i>=k) cout<<a[q.front()]<<" ";
	}
}
 
int main() {
	cin>>n>>k;
	for(int i=1; i<=n; i++) cin>>a[i];
 
	que_min();
	cout<<endl;
	que_max();
	
	return 0;
}
 
/*
input：
8 3
1 3 -1 -3 5 3 6 7

output：
-1 -3 -3 -3 3 3
3 3 5 5 6 7
*/

【参考文献】
https://zhuanlan.zhihu.com/p/447209490
https://www.bilibili.com/video/BV1vv4y1K7qn/
https://sweetlemon.blog.luogu.org/dan-diao-dui-lie
https://www.cnblogs.com/I-Love-You-520/p/13454305.html
https://zhuanlan.zhihu.com/p/346354943
https://blog.csdn.net/weixin_43534024/article/details/88615285
https://blog.csdn.net/hnjzsyjyj/article/details/109680717

?