[数据结构与算法]Go语言学习笔记【13】 排序算法之插入、二分查找插入、希尔排序

【声明】

非完全原创，部分内容来自于学习其他人的理论和B站视频。如果有侵权，请联系我，可以立即删除掉。

一、插入排序

1、方法和复杂度

1.1、核心思想

基于某序列已经有序排列的情况下，通过一次插入一个元素的方式按照原有排序方式增加元素。每次将1个待排序的记录按其关键字大小插入到前面已经排好序的子序列中，寻找最适当的位置，直至全部记录插入完毕。

1.2、主要方法

从该有序序列的最末端开始执行，即要插入序列中的元素最先和有序序列中最大的元素比较，若其大于该最大元素，则可直接插入最大元素的后面即可，否则再向前一位比较查找直至找到应该插入的位置为止。

1.3、稳定性

当待插入元素和插入元素相等的位置，则将待插入的元素放在该相等元素的后面，从而保证了排序的稳定性

1.4、时间复杂度

最优情况：当待排序数组是有序时，只需当前数跟前一个数比较一下就可以了，数组无需移动，这时一共需要比较N-1次，时间复杂度为 $O(N)$
最坏情况：当待排序数组是逆序时，N-1次循环需要移动：1+2+3+..+(N-1) = N*(N-1)/2，时间复杂度为 $O(N^2)$
综合来看，时间复杂度为 $O(N^2)$

1.5、空间复杂度

在整个算法中，只用到了三个辅助变量：i控制外层循环、j控制内层循环、tmp记录待插入的元素。辅助的空间与问题规模无关，因此空间复杂度是 $O(1)$

2、排序的过程

• 第一趟排序。数组的有序区间（只有第一个元素）下标为[0, 0]，此时需要将第二个元素插入到有序区间中，即，将第二个元素和前面的元素进行比较，小于则插入到有序区间的前面（即第一个元素后移一位，第二个元素替换掉第一个元素）；大于或等于，则不进行操作。此时有序区间为[0, 1]
• 第二趟排序。有序区间下标[0, 1]，此时待插入元素为：第三个元素。即，待插入元素按照从后往前的顺序，与有序区间的元素进行比较，小于有序区间的元素则继续往前查找。在有序区间中，找到大于或等于待插入元素的索引k，此时区间[k, 1]整体往后移动1位，然后索引k处的元素用待插入元素替换。
• 依此类推

3、改进思路：有序区间查找用二分查找法

由于每一趟排序，都需要在有序区间中查找待插入元素的位置，因此可以使用二分查找法来提高查找的效率。
该思路只能提高查找效率，并不能减少比较的趟数，也不能减少元素右移的次数，因此时间复杂度不会改变。由于二分查找只需要多引入三个变量：low记录查找区间最小元素索引，high记录查找区间最大元素索引，mid记录查找区间中间元素的索引，因此空间复杂度也不会改变。

4、代码实现

package main

import "fmt"

const size = 10

func Insert(arr *[size]int) {
	var i, j int  //用于两层循环
	cnt := 0      //记录循环/元素比较的次数
	swap_cnt := 0 //记录发生交换的次数
	tmp := 0      //临时变量，记录待插入的元素
	fmt.Println("原数组序列:  ", *arr)
	for i = 1; i < len(arr); i++ {
		//arr数组[0, i-1]是有序，寻找arr[i]的位置
		tmp = arr[i]
		for j = i; j > 0 && arr[j-1] > tmp; j-- {
			arr[j] = arr[j-1] //整体往后移动
			swap_cnt++
		}
		arr[j] = tmp
		cnt += i - j
		fmt.Printf("第[%02d]趟: %v\n", i, *arr)
	}
	fmt.Printf("【Insert】排序的趟数: %d, 排序元素比较的次数: %d, 发生元素交换的次数: %d\n", i-1, cnt, swap_cnt)
}

func BinaryInsert(arr *[size]int) {
	var i, j int           //记录外层循环
	var low, mid, high int //记录待插入的有序区间
	cnt := 0               //记录循环/元素比较的次数
	swap_cnt := 0          //记录发生交换的次数
	tmp := 0               //临时变量，记录待插入的元素
	fmt.Println("原数组序列:  ", *arr)
	for i = 1; i < len(arr); i++ {
		//arr数组[0, i-1]是有序，寻找arr[i]的位置
		tmp = arr[i]
		low, high = 0, i-1
		/*循环最后一轮时，low = high = mid，分为两种情况：
		(1) i所在的元素小于mid元素，则插在mid处，mid及后面元素整体右移
		循环结束时：high + 1 = mid = low，右移区间[low, i-1]
		(2) i所在的元素大于等于mid，则插在mid后一位， mid+1及后面元素整体右移
		循环结束时：high = mid = low - 1，右移区间[low, i-1]
		*/
		for low <= high {
			mid = (low + high) / 2
			//保证稳定性，和中间数相等时，移到中间数后一位
			if arr[i] < arr[mid] {
				high = mid - 1
			} else {
				low = mid + 1
			}
		}
		//有序区间[low, i-1]需要整体右移移位
		for j = i - 1; j >= low; j-- {
			arr[j+1] = arr[j] //整体往后移动
			swap_cnt++
		}
		arr[low] = tmp
		cnt += i - 1 - j
		fmt.Printf("第[%02d]趟: %v\n", i, *arr)
	}
	fmt.Printf("【BinaryInsert】排序的趟数: %d, 排序元素比较的次数: %d, 发生元素交换的次数: %d\n", i-1, cnt, swap_cnt)
}

func main() {
	arr := [size]int{5, 0, 4, 3, 9, 1, 7, 8, 2, 6}
	var arr_tmp [size]int = arr

	Insert(&arr_tmp)
	arr_tmp = arr
	BinaryInsert(&arr_tmp)
}

5、运行结果

原数组序列:   [5 0 4 3 9 1 7 8 2 6]
第[01]趟: [0 5 4 3 9 1 7 8 2 6]
第[02]趟: [0 4 5 3 9 1 7 8 2 6]
第[03]趟: [0 3 4 5 9 1 7 8 2 6]
第[04]趟: [0 3 4 5 9 1 7 8 2 6]
第[05]趟: [0 1 3 4 5 9 7 8 2 6]
第[06]趟: [0 1 3 4 5 7 9 8 2 6]
第[07]趟: [0 1 3 4 5 7 8 9 2 6]
第[08]趟: [0 1 2 3 4 5 7 8 9 6]
第[09]趟: [0 1 2 3 4 5 6 7 8 9]
【Insert】排序的趟数: 9, 排序元素比较的次数: 19, 发生元素交换的次数: 19
原数组序列:   [5 0 4 3 9 1 7 8 2 6]
第[01]趟: [0 5 4 3 9 1 7 8 2 6]
第[02]趟: [0 4 5 3 9 1 7 8 2 6]
第[03]趟: [0 3 4 5 9 1 7 8 2 6]
第[04]趟: [0 3 4 5 9 1 7 8 2 6]
第[05]趟: [0 1 3 4 5 9 7 8 2 6]
第[06]趟: [0 1 3 4 5 7 9 8 2 6]
第[07]趟: [0 1 3 4 5 7 8 9 2 6]
第[08]趟: [0 1 2 3 4 5 7 8 9 6]
第[09]趟: [0 1 2 3 4 5 6 7 8 9]
【BinaryInsert】排序的趟数: 9, 排序元素比较的次数: 19, 发生元素交换的次数: 19

二、希尔排序

希尔排序(Shell’s Sort)是插入排序的一种又称“缩小增量排序”（Diminishing Increment Sort），是直接插入排序算法的一种更高效的改进版本。它是一种非稳定的排序算法

1、方法和复杂度

1.1、核心思想

先取整数d1(d1 < n)作为第一个增量，把文件的全部记录分组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序；
然后再取整数d2(d2 < d1)作为第二个增量，把文件的全部记录分组。所有距离为d2的倍数的记录放在同一个组中，各组内进行插入排序；
循环上面的做法，直到增量dk = 1时，整个文件的记录作为一组，进行插入排序

1.2、主要方法

设置增量step（也叫间隔、步长），初值一般是数组长度的一半（step = len(arr)/2），然后根据增量对数组进行分组，各个组在组内进行插入排序；
接着增量设为上一次的一半step/2，根据增量对数组进行分组，各个组在组内进行插入排序；
依此类推，直到增量为0时结束

1.3、稳定性

由于同一组内的元素都是间隔step，因此只能保证同一个组内的排序是稳定的，整个数组的排序是不稳定的。举例：
假如有数组{5, 9, 4, 4, 3, 6}，数组长度为6。第一次的增量为3，数组被分为3组。在进行第一次排序之后，原来索引为3的数值4变为索引0了，而索引为2的数值4位置不变，因此排序的过程是 不稳定 的

5        4							4        5
   9        3		--第1次排序后--	   3        9
      4        6				  	  	  4        6

1.4、时间复杂度

最优情况：当待排序数组是有序时，每一次分组之后数组元素只需要进行比较，但数组的元素无需移动，时间复杂度为 $O(N^{1.3})$
最坏情况：当待排序数组是逆序时，每一次比较都需要移动数组元素，时间复杂度为 $O(N^2)$
综合来看，时间复杂度 介于 $O(N)$ 和 $O(N^2)$。具体的分析，详见 希尔排序复杂度详细分析

1.5、空间复杂度

算法中，只用到了几个辅助变量，因此空间复杂度是 $O(1)$

2、排序的过程

以数组{5, 4, 3, 0, 9, 1, 7, 8, 2, 6}为例，数组长度为10

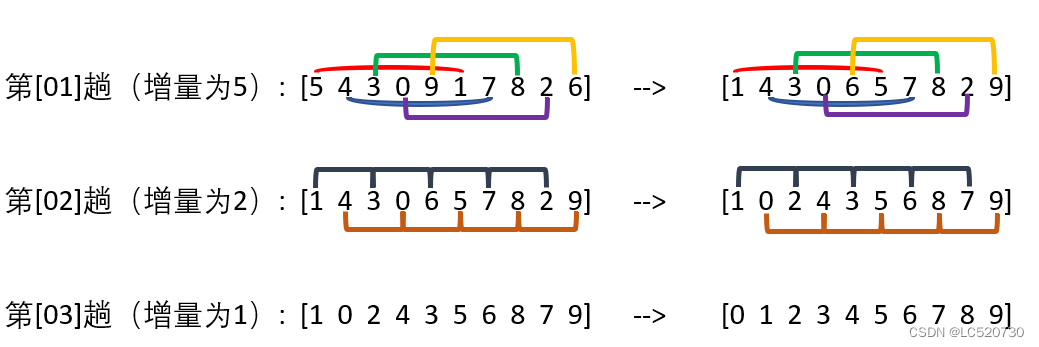
3、实现的代码

func Shell(arr *[size]int) {
	var step, i, j int //记录step, 外层, 内层循环
	sum := 0           //记录趟数
	cnt := 0           //记录循环/元素比较的次数
	swap_cnt := 0      //记录发生交换的次数
	tmp := 0           //临时变量，记录待插入的元素
	fmt.Println("原数组序列:  ", *arr)
	for step = len(arr) / 2; step > 0; step /= 2 {
		//下标[0, step, 2*step, ...]为第一组需要快速排序的数组
		for i = step; i < len(arr); i++ {
			tmp = arr[i] //记录待插元素
			for j = i; j >= step && arr[j-step] > arr[j]; j -= step {
				arr[j-step], arr[j] = arr[j], arr[j-step]
				swap_cnt++
			}
			arr[j] = tmp
			cnt += (i - j) / step
		}
		sum++
		fmt.Printf("第[%02d]趟: %v\n", sum, *arr)
	}
	fmt.Printf("【Shell】排序的趟数: %d, 排序元素比较的次数: %d, 发生元素交换的次数: %d\n", sum, cnt, swap_cnt)
}

func main() {
	arr := [size]int{5, 4, 3, 0, 9, 1, 7, 8, 2, 6}
	var arr_tmp [size]int = arr
	arr_tmp = arr
	Shell(&arr_tmp)
}

4、运行结果

原数组序列:   [5 4 3 0 9 1 7 8 2 6]
第[01]趟: [1 4 3 0 6 5 7 8 2 9]
第[02]趟: [1 0 2 4 3 5 6 8 7 9]
第[03]趟: [0 1 2 3 4 5 6 7 8 9]
【Shell】排序的趟数: 3, 排序元素比较的次数: 9, 发生元素交换的次数: 9