1.什么是堆？大根堆？小根堆？
堆：堆是一棵完全二叉树
大根堆：若根节点存在左右子节点，那么根节点的值大于或等于左右子节点的值
小根堆：若根节点存在左右子节点，那么根节点的值小于或等于左右子节点的值
2.哈夫曼编码？
哈夫曼（Huffman）编码算法是基于二叉树构建编码压缩结构的，它是数据压缩中经典的一种算法。算法根据文本字符出现的频率，重新对字符进行编码。因为为了缩短编码的长度，我们自然希望频率越高的词，编码越短，这样最终才能最大化压缩存储文本数据的空间。
我们使用二叉树来构建哈夫曼树并生成哈夫曼编码. 实际上,哈夫曼树构造的过程就是最优二叉树的构建过程
原文链接：https://blog.csdn.net/wintershii/article/details/84898214
3.快速排序？
时间复杂度：O（nlogn）
原理：每次找出一个监视哨，然后遍历数据，将数据分为两部分，比监视哨小的放到监视哨的左边位置，比监视哨大的放到监视哨的右边位置。
数组和链表的区别？
4.循环队列的优点和缺点？
优点：相对于直线队列来讲，直线队列在元素出队后，头指针向后移动，导致删除元素后的空间无法在利用，即使元素个数小于空间大小，依然无法再进行插入，即所谓的“假上溢”。当变成循环队列之后，删除元素后的空间仍然可以利用，最大限度的利用空间。
缺点：无法通过front==real来判断满或空，可以将一个位置单独作为哨兵位来解决
5.各种排序算法时间复杂度？
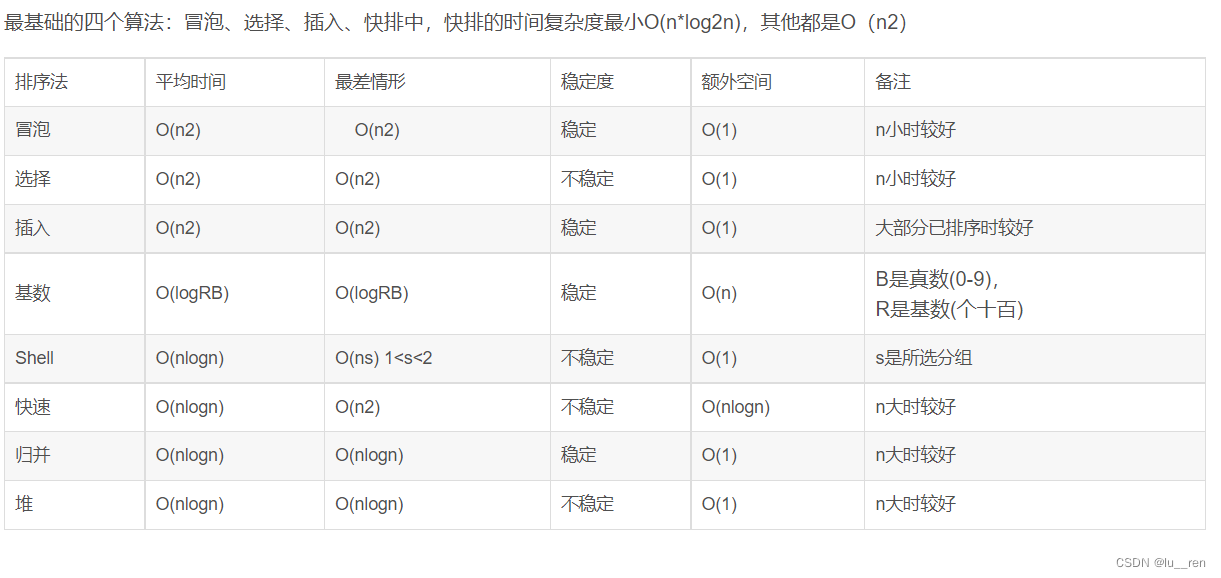各排序算法的思想：
(1)冒泡排序：
是相邻元素之间的比较和交换，两重循环O(n2)；所以，如果两个相邻元素相等，是不会交换的。所以它是一种稳定的排序方法
(2)选择排序：
每个元素都与第一个元素相比，产生交换，两重循环O(n2)；举个栗子，5 8 5 2 9，第一遍之后，2会与5交换，那么原序列中两个5的顺序就被破坏了。所以不是稳定的排序算法
(3)插入排序：
插入排序是在一个已经有序的小序列的基础上，一次插入一个元素。刚开始这个小序列只包含第一个元素，事件复杂度O(n2)。比较是从这个小序列的末尾开始的。想要插入的元素和小序列的最大者开始比起，如果比它大则直接插在其后面，否则一直往前找它该插入的位置。如果遇见了一个和插入元素相等的，则把插入元素放在这个相等元素的后面。所以相等元素间的顺序没有改变，是稳定的。
(4)快速排序
快速排序有两个方向，左边的i下标一直往右走，当a[i] <= a[center_index]，其中center_index是中枢元素的数组下标，一般取为数组第0个元素。而右边的j下标一直往左走，当a[j] > a[center_index]。如果i和j都走不动了，i <= j, 交换a[i]和a[j],重复上面的过程，直到i>j。 交换a[j]和a[center_index]，完成一趟快速排序。在中枢元素和a[j]交换的时候，很有可能把前面的元素的稳定性打乱，比如序列为 5 3 3 4 3 8 9 10 11， 现在中枢元素5和3(第5个元素，下标从1开始计)交换就会把元素3的稳定性打乱，所以快速排序是一个不稳定的排序算法，不稳定发生在中枢元素和a[j]交换的时刻。
(5)归并排序
归并排序是把序列递归地分成短序列，递归出口是短序列只有1个元素(认为直接有序)或者2个序列(1次比较和交换),然后把各个有序的段序列合并成一个有序的长序列，不断合并直到原序列全部排好序。可以发现，在1个或2个元素时，1个元素不会交换，2个元素如果大小相等也没有人故意交换，这不会破坏稳定性。那么，在短的有序序列合并的过程中，稳定是是否受到破坏？没有，合并过程中我们可以保证如果两个当前元素相等时，我们把处在前面的序列的元素保存在结果序列的前面，这样就保证了稳定性。所以，归并排序也是稳定的排序算法。
(6)基数排序
基数排序是按照低位先排序，然后收集；再按照高位排序，然后再收集；依次类推，直到最高位。有时候有些属性是有优先级顺序的，先按低优先级排序，再按高优先级排序，最后的次序就是高优先级高的在前，高优先级相同的低优先级高的在前。基数排序基于分别排序，分别收集，所以其是稳定的排序算法。
(7)希尔排序(shell)
希尔排序是按照不同步长对元素进行插入排序，当刚开始元素很无序的时候，步长最大，所以插入排序的元素个数很少，速度很快；当元素基本有序了，步长很小，插入排序对于有序的序列效率很高。所以，希尔排序的时间复杂度会比o(n^2)好一些。由于多次插入排序，我们知道一次插入排序是稳定的，不会改变相同元素的相对顺序，但在不同的插入排序过程中，相同的元素可能在各自的插入排序中移动，最后其稳定性就会被打乱，所以shell排序是不稳定的。
(8)堆排序
我们知道堆的结构是节点i的孩子为2i和2i+1节点，大顶堆要求父节点大于等于其2个子节点，小顶堆要求父节点小于等于其2个子节点。在一个长为n的序列，堆排序的过程是从第n/2开始和其子节点共3个值选择最大(大顶堆)或者最小(小顶堆),这3个元素之间的选择当然不会破坏稳定性。但当为n/2-1, n/2-2, …1这些个父节点选择元素时，就会破坏稳定性。有可能第n/2个父节点交换把后面一个元素交换过去了，而第n/2-1个父节点把后面一个相同的元素没有交换，那么这2个相同的元素之间的稳定性就被破坏了。所以，堆排序不是稳定的排序算法
原文链接：https://blog.csdn.net/q2213065359/article/details/82801717
6.数组和链表的区别？
数组和链表是两种基本的数据结构，他们在内存存储上的表现不一样，所以也有各自的特点
数组
一、数组的特点
1.在内存中，数组是一块连续的区域
2.数组需要预留空间
在使用前需要提前申请所占内存的大小，这样不知道需要多大的空间，就预先申请可能会浪费内存空间，即数组空间利用率低
ps：数组的空间在编译阶段就需要进行确定，所以需要提前给出数组空间的大小（在运行阶段是不允许改变的）
3.在数组起始位置处，插入数据和删除数据效率低。
插入数据时，待插入位置的的元素和它后面的所有元素都需要向后搬移
删除数据时，待删除位置后面的所有元素都需要向前搬移
4.随机访问效率很高，时间复杂度可以达到O(1)
因为数组的内存是连续的，想要访问那个元素，直接从数组的首地址处向后偏移就可以访问到了
5.数组开辟的空间，在不够使用的时候需要扩容，扩容的话，就会涉及到需要把旧数组中的所有元素向新数组中搬移
6.数组的空间是从栈分配的
二、数组的优点
随机访问性强，查找速度快，时间复杂度为O(1)
三、数组的缺点
1.头插和头删的效率低，时间复杂度为O(N)
2.空间利用率不高
3.内存空间要求高，必须有足够的连续的内存空间
4.数组空间的大小固定，不能动态拓展
链表
一、链表的特点
1.在内存中，元素的空间可以在任意地方，空间是分散的，不需要连续
2.链表中的元素都会两个属性，一个是元素的值，另一个是指针，此指针标记了下一个元素的地址
每一个数据都会保存下一个数据的内存的地址，通过此地址可以找到下一个数据
3.查找数据时效率低,时间复杂度为O(N)
因为链表的空间是分散的，所以不具有随机访问性，如要需要访问某个位置的数据，需要从第一个数据开始找起，依次往后遍历，直到找到待查询的位置，故可能在查找某个元素时，时间复杂度达到O(N)
4.空间不需要提前指定大小，是动态申请的，根据需求动态的申请和删除内存空间，扩展方便，故空间的利用率较高
5.任意位置插入元素和删除元素效率较高，时间复杂度为O(1)
6.链表的空间是从堆中分配的
二、链表的优点
1.任意位置插入元素和删除元素的速度快，时间复杂度为O(1)
2.内存利用率高，不会浪费内存
3.链表的空间大小不固定，可以动态拓展
三、链表的缺点
随机访问效率低，时间复杂度为0(N)
综上：
对于想要快速访问数据，不经常有插入和删除元素的时候，选择数组
对于需要经常的插入和删除元素，而对访问元素时的效率没有很高要求的话，选择链表
原文链接：https://zhuanlan.zhihu.com/p/78165368
7.邻接矩阵与邻接表？
都是对图的一种数据存储方式。
邻接矩阵：就是一个二维数组，大小为dis[n][n]（n为顶点数），其中dis[i][j]表示顶点i到顶点j的距离，可以看出，邻接表的空间复杂度为O(n^2)，
邻接表：邻接表是一部分人理解的难点，它的思想是，对每一个顶点，创建一个表，链接其所有出边。
8.解决哈希冲突的方法？
1）开放定址法：
这种方法也称再散列法，其基本思想是：当关键字key的哈希地址p=H（key）出现冲突时，以p为基础，产生另一个哈希地址p1，如果p1仍然冲突，再以p为基础，产生另一个哈希地址p2，…，直到找出一个不冲突的哈希地址pi ，将相应元素存入其中。这种方法有一个通用的再散列函数形式：
Hi=（H（key）+di）% m i=1，2，…，n
其中H（key）为哈希函数，m 为表长，di称为增量序列。增量序列的取值方式不同，相应的再散列方式也不同。主要有以下三种：
线性探测再散列
dii=1，2，3，…，m-1
这种方法的特点是：冲突发生时，顺序查看表中下一单元，直到找出一个空单元或查遍全表。
二次探测再散列
di=12，-12，22，-22，…，k2，-k2 ( k<=m/2 )
这种方法的特点是：冲突发生时，在表的左右进行跳跃式探测，比较灵活。
伪随机探测再散列
di=伪随机数序列。
具体实现时，应建立一个伪随机数发生器，（如i=(i+p) % m），并给定一个随机数做起点。
例如，已知哈希表长度m=11，哈希函数为：H（key）= key % 11，则H（47）=3，H（26）=4，H（60）=5，假设下一个关键字为69，则H（69）=3，与47冲突。
如果用线性探测再散列处理冲突，下一个哈希地址为H1=（3 + 1）% 11 = 4，仍然冲突，再找下一个哈希地址为H2=（3 + 2）% 11 = 5，还是冲突，继续找下一个哈希地址为H3=（3 + 3）% 11 = 6，此时不再冲突，将69填入5号单元。
如果用二次探测再散列处理冲突，下一个哈希地址为H1=（3 + 12）% 11 = 4，仍然冲突，再找下一个哈希地址为H2=（3 - 12）% 11 = 2，此时不再冲突，将69填入2号单元。
如果用伪随机探测再散列处理冲突，且伪随机数序列为：2，5，9，………，则下一个哈希地址为H1=（3 + 2）% 11 = 5，仍然冲突，再找下一个哈希地址为H2=（3 + 5）% 11 = 8，此时不再冲突，将69填入8号单元。
- 再哈希法
这种方法是同时构造多个不同的哈希函数：
Hi=RH1（key） i=1，2，…，k
当哈希地址Hi=RH1（key）发生冲突时，再计算Hi=RH2（key）……，直到冲突不再产生。这种方法不易产生聚集，但增加了计算时间。
3）链地址法
这种方法的基本思想是将所有哈希地址为i的元素构成一个称为同义词链的单链表，并将单链表的头指针存在哈希表的第i个单元中，因而查找、插入和删除主要在同义词链中进行。链地址法适用于经常进行插入和删除的情况。
4）建立公共溢出区
这种方法的基本思想是：将哈希表分为基本表和溢出表两部分，凡是和基本表发生冲突的元素，一律填入溢出表。