目录
红黑树的概念及结构
概念
? ?红黑树也是一种二叉排序树，在红黑树中每个结点存储着对应的颜色(红色或者黑色)，由于AVL树的高度平衡是因为非常频繁地调用旋转来保存自身平衡的，代价较大。所以在AVL树的基础上进一步放宽条件，引入红黑树，即红黑树的最长路径不会比最短路径长两倍。
一棵红黑树需要满足以下性质才能保证最长路径不会超过最短路径的两倍：
1，根结点必须是黑色，其他结点不是黑色就是红色
2，红色结点的双亲结点与孩子结点都是黑色的，也就是不会存在两个相邻的红色结点
3，对于每一个结点，从该结点到任一叶结点的路径上，每条路径上的黑色结点数量相同
4，空结点为黑色
通过上面的性质可以得出一些结论：
1，最短路径上的结点都是黑色的，而最长路径上的结点一黑一红交替
2，若一棵红黑树有n个结点则红黑树的高度为h <= 2*log(2) (n+1)
3，在红黑树中，对于红色结点其出度只能为0或者2
4，在红黑树中，如果黑色结点只有一个孩子结点，则该孩子结点只能为红色
结构
? ?红黑树的链式结构依然用三叉链，红黑树的每一个结点都存储着左孩子结点地址，右孩子结点地址，双亲结点地址，KeyValue数据以及结点的颜色。
? ?新开辟的结点默认选择是红色的：假设新插入的结点默认是黑色的，那么这个结点所在的路径会比其他路径多一个黑色的结点，会破坏性质3，调整起来很麻烦。如果插入的结点默认是红色的，所有路径上的黑色结点数量依然相同，如果插入结点的双亲是黑色的则不需要处理直接结束插入，如果插入结点的双亲是红色的则破坏性质2需要处理。所以选择新插入的结点为红色的代价小。
红黑树的插入
? ?红黑树的插入思路与二叉搜索树的插入相同，只不过红黑树需要在插入新结点之后，判断插入之后有没有违反红黑树的性质。如果没有违反则插入成功，否则需要进行修复使之平衡。
第一步：找到新结点的插入位置，并记录新结点的双亲位置
第二步：进行插入，如果新结点小于双亲则往左插入，如果新结点大于双亲则往右插入?
第三步：判断是否需要修复，如果双亲结点的颜色为黑色则不需要修复，如果双亲结点的颜色为红色则需要修复?
当双亲的颜色为红色时，需要进行修复，而修复的方法分为两种，这两种方法是根据其插入结点的叔叔来决定的。
1，当叔叔存在并且为红时，进行调色然后继续往上处理------祖父变为红色，双亲与叔叔变为黑色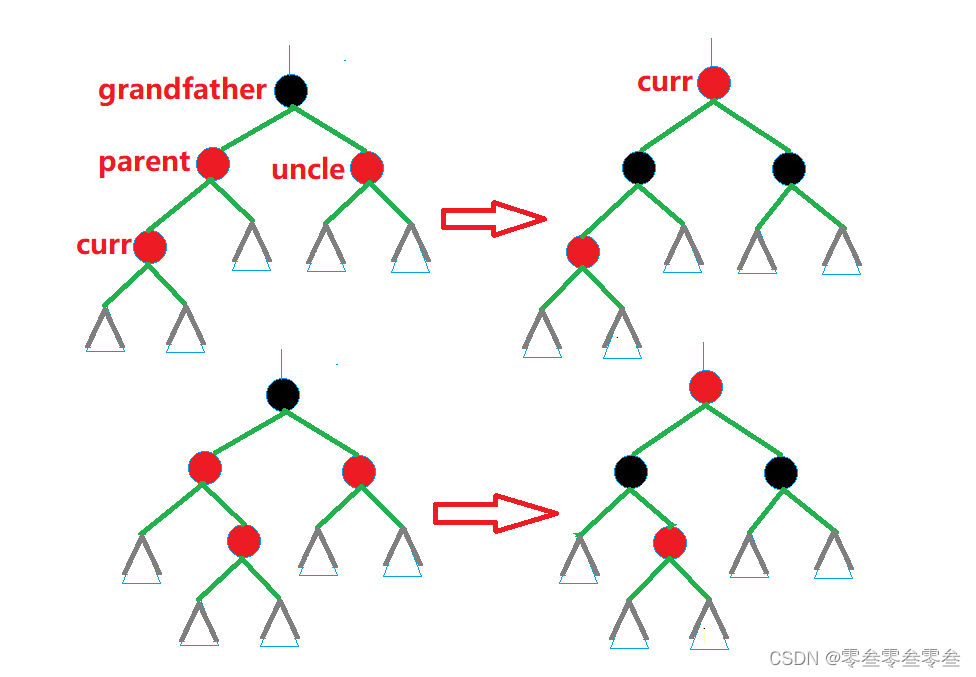
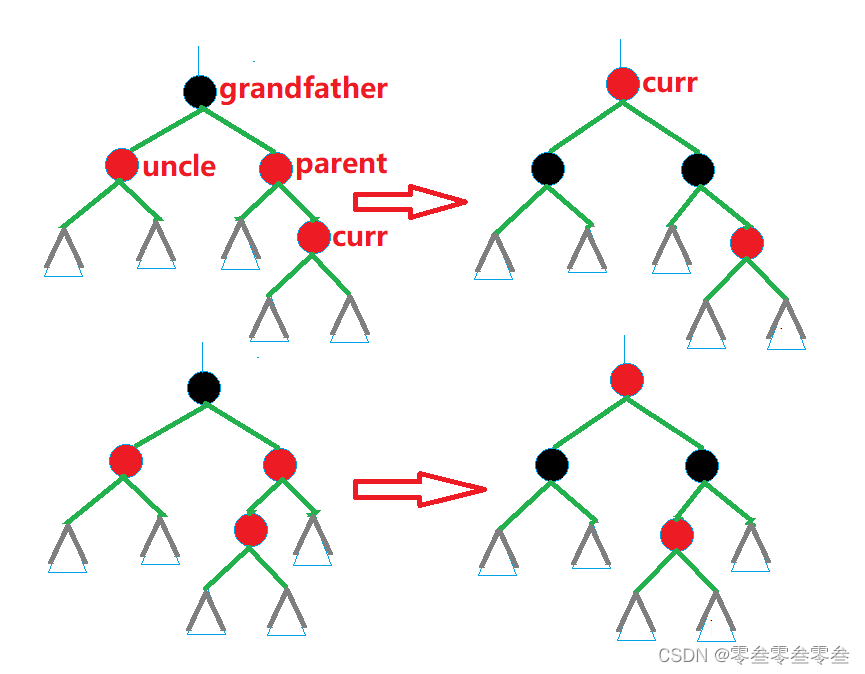2，当叔叔不存在或者叔叔的颜色为黑，需要进行旋转与调色处理------（1，双亲是祖父的左孩子并且新插入结点是双亲的左孩子，进行祖父右旋转并将祖父变为红，双亲变为黑。（2，双亲是祖父的左孩子并且新插入结点是双亲的右孩子，进行双亲左旋转祖父右旋转，并将祖父变红，新插入结点变黑。（3，双亲是祖父的右孩子并且新插入结点是双亲的右孩子，进行祖父左旋转并将祖父变为红色，双亲变为黑色。（4，双亲是祖父的右孩子并且新插入结点是双亲的左孩子，进行双亲右旋转祖父左旋转，并将祖父变为红色，新插入结点变为黑色。
// 旋转代码
//右旋转
void RotateR(Node* root)
{
Node* subL = root->_left;
Node* subLR = subL->_right;
Node* rootParent = root->_parent;
subL->_right = root;
root->_parent = subL;
root->_left = subLR;
if (subLR)
{
subLR->_parent = root;
}
if (rootParent == nullptr)
{
_root = subL;
subL->_parent=nullptr;
}
else
{
if (rootParent->_left == root)
{
rootParent->_left = subL;
}
else if (rootParent->_right == root)
{
rootParent->_right = subL;
}
subL->_parent = rootParent;
}
}
// 左旋转
void RotateL(Node* root)
{
Node* subR = root->_right;
Node* subRL = subR->_left;
Node* rootParent = root->_parent;
subR->_left = root;
root->_parent = subR;
root->_right = subRL;
if (subRL)
{
subRL->_parent = root;
}
if (rootParent == nullptr)
{
_root = subR;
subR->_parent = nullptr;
}
else
{
if (rootParent->_left == root)
{
rootParent->_left = subR;
}
else if (rootParent->_right == root)
{
rootParent->_right = subR;
}
subR->_parent = rootParent;
}
}最后将根结点的颜色变为黑色。
pair<Node*,bool> Insert(const pair<K, V>& kv)
{
if (_root == nullptr) // 根结点为空，直接插入
{
_root = new Node(kv); // 新结点的地址给_root记录
_root->_parent = nullptr; // 根结点的双亲为空
_root->_colour = BLACK; // 根结点颜色变为黑色
return make_pair(_root, true); // 返回成功插入的结点
}
Node* parent = nullptr; // 记录插入位置的双亲结点
Node* curr = _root; // 寻找插入的位置
while (curr) // curr为空表示找到了插入的位置
{
if (curr->_kv.first > kv.first) // 往左寻找
{
parent = curr;
curr=curr->_left;
}
else if (curr->_kv.first < kv.first) // 往右寻找
{
parent = curr;
curr = curr->_right;
}
else // 已经有对应数据的结点，插入失败
{
return make_pair(curr, false); // 返回已经有对应数据的结点
}
}
Node* newNode = new Node(kv); // 开辟红色新结点，开始插入
if (parent->_kv.first > kv.first) // 比双亲小，往左边插入
{
parent->_left = newNode;
}
else if(parent->_kv.first<kv.first) // 比双亲大，往右边插入
{
parent->_right = newNode;
}
newNode->_parent = parent; // 让新结点的_parent指向双亲
curr = newNode; // curr为新插入的结点，parent为新插入结点的双亲
while (parent && parent->_colour == RED) // 如果新插入结点的双亲为红色则需要调整
{
Node* grandFather = parent->_parent; // 红色结点一定有双亲
if (grandFather->_left == parent) // 叔叔是祖父的右孩子
{
Node* uncle = grandFather->_right;
if (uncle && uncle->_colour == RED) // 叔叔存在而且颜色为红
{
//双亲与叔叔颜色变黑
parent->_colour = uncle->_colour = BLACK;
grandFather->_colour = RED; // 祖父颜色变红
// 迭代
curr = grandFather;
parent = curr->_parent;
}
else // 叔叔不存在或者叔叔颜色为黑
{
if (parent->_left == curr) // 左左---右单选
{
RotateR(grandFather); // 旋转祖父
grandFather->_colour = RED;
parent->_colour = BLACK;
}
else // 左右---左右双旋
{
RotateL(parent); // 先旋转双亲
RotateR(grandFather); // 再旋转祖父
grandFather->_colour = RED; // 祖父变红
curr->_colour = BLACK; // 新插入的结点变黑
}
break;
}
}
else if(grandFather->_right==parent) // 叔叔是祖父的左孩子
{
Node* uncle = grandFather->_left;
if (uncle && uncle->_colour== RED) // 叔叔存在而且颜色为红
{
// 调色加继续向上处理
parent->_colour = uncle->_colour = BLACK;
grandFather->_colour = RED;
// 迭代
curr = grandFather;
parent = curr->_parent;
}
else // 叔叔不存在或者叔叔颜色为黑
{
// 调色加旋转，结束处理
if (parent->_right == curr) // 右右---左单选
{
RotateL(grandFather);
grandFather->_colour = RED;
parent->_colour = BLACK;
}
else // 右左---右左双旋
{
RotateR(parent);
RotateL(grandFather);
grandFather->_colour = RED;
curr->_colour = BLACK;
}
break;
}
}
}
_root->_colour = BLACK; // 将根结点变为黑色
return make_pair(newNode, true); // 插入成功，返回插入结点
}红黑树的删除
第一步：找到要删除的结点
第二步：按照要删除结点的类型进行分类删除：1，左子树为空? ?2，右子树为空? ?3，左右子树都为空? ?4，左右子树都不为空
第三步：在删除之前，根据删除结点的特征与颜色进行调整
1，如果删除的结点是红色
可以直接删除，不会影响红黑树的特性
2，如果删除的结点是黑色，并且有一个孩子结点（孩子结点一定是红色）
则将该黑色结点删除，并将该孩子结点变红交给双亲托管
3，如果删除的结点是黑色，并且兄弟结点是黑色，其远侄子是红色
交换双亲与兄弟的颜色，并且将远侄子的颜色变为黑色，双亲进行一次单旋转（删除结点在双亲的左进行左旋转；删除结点在双亲的右进行右旋转）；完成之后3特征结束
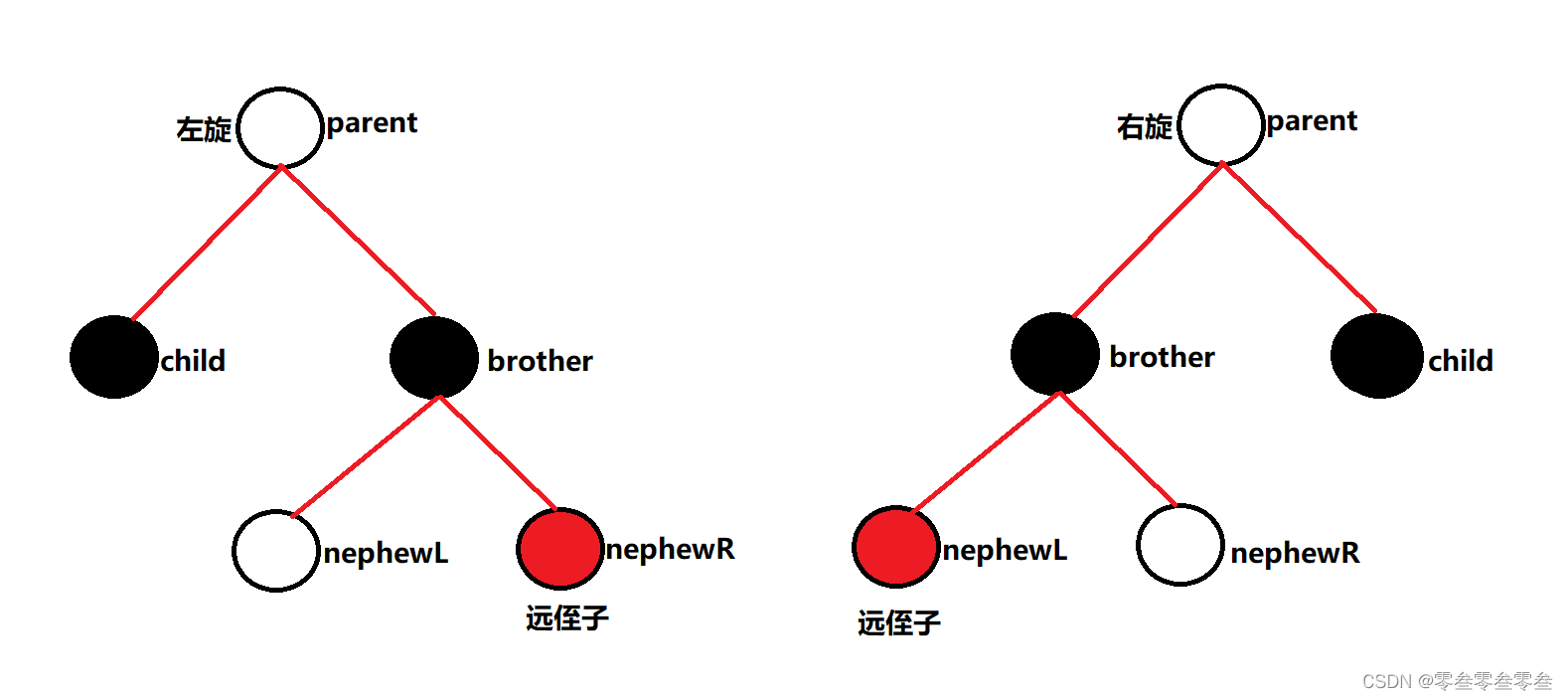
4，如果删除结点是黑色，并且兄弟结点是黑色，近侄子是红色，远侄子是黑色
兄弟与近侄子交换颜色，然后对兄弟做一次单旋转（删除结点在双亲的左进行右旋转；删除结点在双亲的右进行左旋转）；完成之后4特征变为3特征继续
5，如果删除的结点是黑色，并且兄弟结点的颜色是红色
交换双亲与兄弟的颜色，然后对双亲做一次单旋转（删除结点在双亲的左进行左旋转；删除结点在双亲的右进行右旋转）这样完成之后5特征变为3特征或者4特征孩子6特征继续
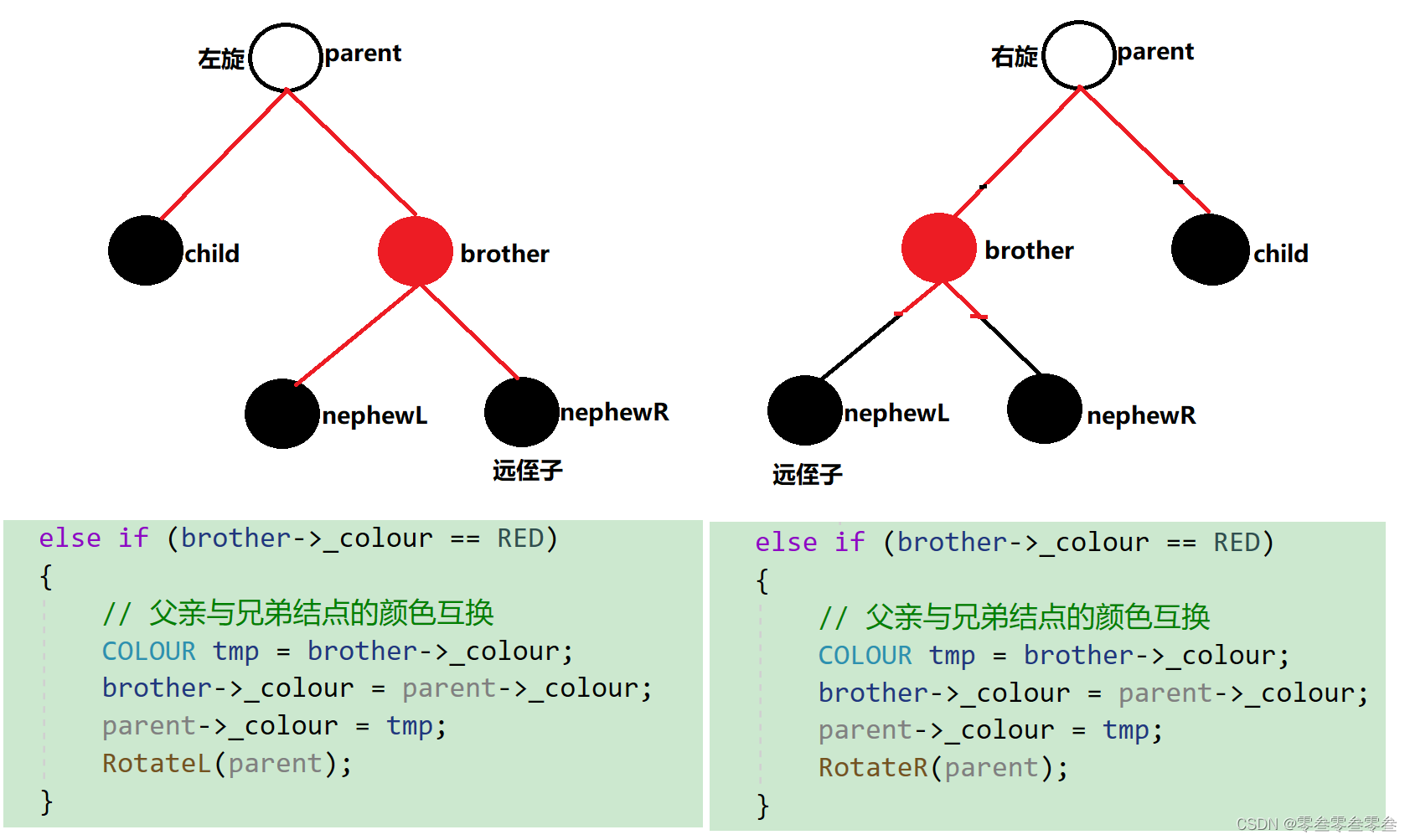
6，如果删除的结点是黑色，兄弟结点是黑色并且其左右孩子都是黑色（左右孩子可以为空）
将兄弟结点变为红色，紧接着判断双亲是否为根结点或者是否为红色，如果成立调整结束，如果不成立将child变为parent，parent变为child->_parent继续往上一层调整
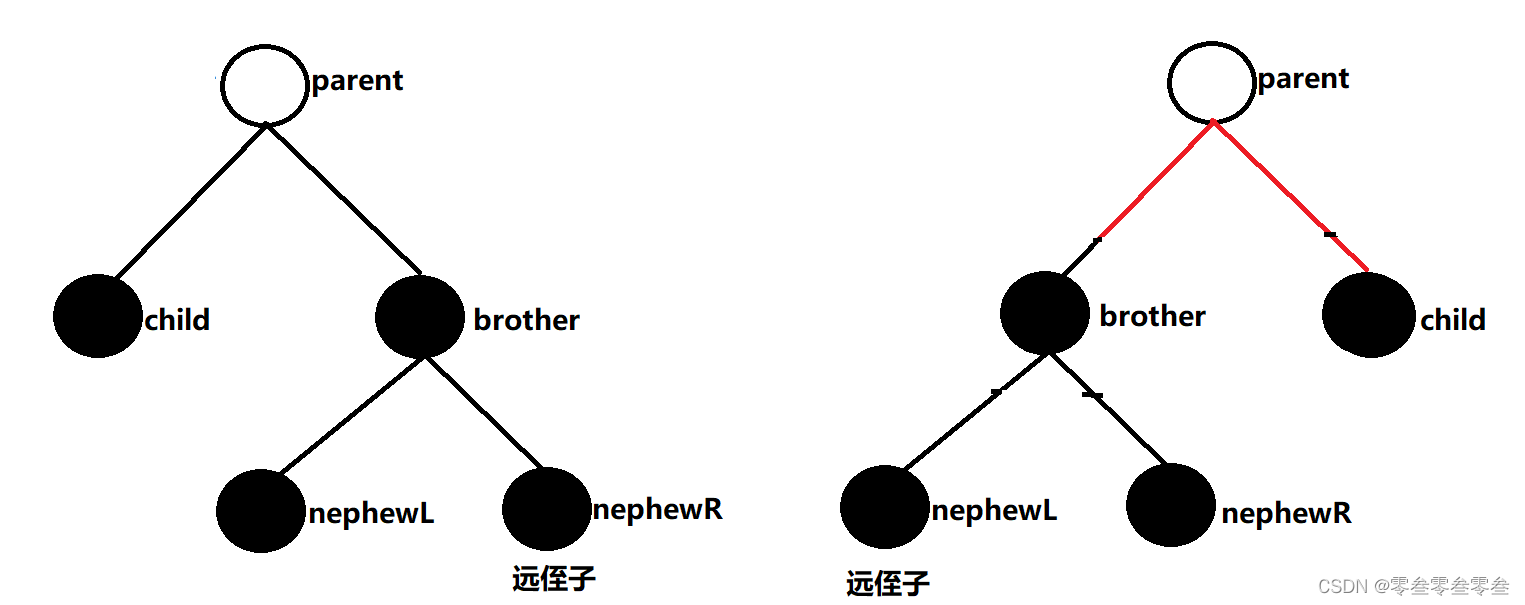
要删除的结点只能也只有这样的特征，其他特征都不存在。
void UpdateB(Node* child, Node* parent)
{
if (child->_colour == RED) // 删除结点为红色
{
return;
}
if (child->_colour==BLACK) // 删除结点为黑色并且有一个孩子
{
if (child->_left && child->_left->_colour==RED)
{
child->_left->_colour = BLACK;
return;
}
else if (child->_right && child->_right->_colour==RED)
{
child->_right->_colour = BLACK;
return;
}
}
while (child!=_root) // 删除结点为黑色没有孩子
{
if (child == parent->_left)
{
Node* brother = parent->_right;
Node* nephewL = brother->_left;
Node* nephewR = brother->_right;
if (brother->_colour == BLACK && nephewR && nephewR->_colour == RED)
{
// 父亲与兄弟结点的颜色互换
COLOUR tmp = brother->_colour;
brother->_colour = parent->_colour;
parent->_colour = tmp;
nephewR->_colour = BLACK; // 兄弟的右孩子换成黑色
RotateL(parent); // 父亲左旋转
return;
}
else if (brother->_colour == BLACK && nephewL && nephewL->_colour == RED)
{
// 兄弟与兄弟左孩子结点的颜色互换
COLOUR tmp = brother->_colour;
brother->_colour = nephewL->_colour;
nephewL->_colour = tmp;
// 兄弟右旋转
RotateR(brother);
}
else if (brother->_colour == BLACK
&& (nephewL == nullptr || nephewL->_colour == BLACK)
&& (nephewR == nullptr || nephewR->_colour == BLACK))
{
brother->_colour = RED;
if (parent == _root || parent->_colour == RED)
{
parent->_colour = BLACK;
return;
}
//向上调整
child = parent;
parent = child->_parent;
}
else if (brother->_colour == RED)
{
// 父亲与兄弟结点的颜色互换
COLOUR tmp = brother->_colour;
brother->_colour = parent->_colour;
parent->_colour = tmp;
RotateL(parent);
}
}
else if(child==parent->_right)
{
Node* brother = parent->_left;
Node* nephewL = brother->_left;
Node* nephewR = brother->_right;
if (brother->_colour == BLACK && nephewL && nephewL->_colour == RED)
{
// 父亲与兄弟结点的颜色互换
COLOUR tmp = brother->_colour;
brother->_colour = parent->_colour;
parent->_colour = tmp;
nephewL->_colour = BLACK; // 兄弟的左孩子换成黑色
RotateR(parent); // 父亲右旋转
return;
}
else if (brother->_colour == BLACK && nephewR && nephewR->_colour == RED)
{
// 兄弟与兄弟右孩子结点的颜色互换
COLOUR tmp = brother->_colour;
brother->_colour = nephewR->_colour;
nephewR->_colour = tmp;
// 兄弟左旋转
RotateL(brother);
}
else if (brother->_colour == BLACK
&& (nephewL == nullptr || nephewL->_colour == BLACK)
&& (nephewR == nullptr || nephewR->_colour == BLACK))
{
brother->_colour = RED;
if (parent == _root || parent->_colour == RED)
{
parent->_colour = BLACK;
return;
}
//向上调整
child = parent;
parent = child->_parent;
}
else if (brother->_colour == RED)
{
// 父亲与兄弟结点的颜色互换
COLOUR tmp = brother->_colour;
brother->_colour = parent->_colour;
parent->_colour = tmp;
RotateR(parent);
}
}
}
}
bool Erase(const K& key)
{
if (_root == nullptr) // 红黑树为空不需要删除
{
return false;
}
Node* parent = nullptr;
Node* curr = _root;
while (curr)
{
if (curr->_kv.first > key) // 往左寻找
{
parent = curr;
curr = curr->_left;
}
else if(curr->_kv.first<key) // 往右寻找
{
parent = curr;
curr = curr->_right;
}
else // 找到了开始删除
{
if (curr->_left == nullptr) // 删除结点的左孩子为空
{
if (curr == _root) // 删除的是根结点
{
_root = curr->_right;
if (_root)
{
_root->_parent = nullptr;
_root->_colour = BLACK;
}
}
else // 删除的不是根结点
{
UpdateB(curr, parent); // 删除之前进行调整
if (parent->_left == curr)
{
parent->_left = curr->_right;
}
else
{
parent->_right = curr->_right;
}
if (curr->_right)
{
curr->_right->_parent = parent;
}
}
delete curr;
return true;
}
else if (curr->_right == nullptr) // 删除结点的右孩子为空
{
if (curr == _root) // 删除的是根结点
{
_root = curr->_left;
if (_root)
{
_root->_parent = nullptr;
_root->_colour = BLACK;
}
}
else // 删除的不是根结点
{
UpdateB(curr, parent); // 删除之前进行判断调整
if (parent->_left == curr)
{
parent->_left = curr->_left;
}
else
{
parent->_right = curr->_left;
}
if (curr->_left)
{
curr->_left->_parent = parent;
}
}
delete curr;
return true;
}
else // 删除结点的左右孩子都不空，进行替换删除
{
Node* min = curr->_right;
while (min->_left)
{
min = min->_left;
}
pair<K, V> tmp = min->_kv;
Erase(tmp.first);
curr->_kv = tmp;
return true;
}
}
}
return false;
}判断是否为红黑树
? ?判断一棵树是否为红黑树只需要验证这颗树是否满足红黑树的性质
bool IsRedBlackTree()
{
Node* pRoot = _root;
// 空树也是红黑树
if (nullptr == pRoot)
return true;
// 检测根节点是否满足情况
if (BLACK != pRoot->_colour)
{
return false;
}
int blackcount = 0; // 先计算一条路径上的黑色数量为基准
Node* curr = _root;
while (curr)
{
if (curr->_colour==BLACK)
{
blackcount++;
}
curr = curr->_left;
}
return _IsRedBlackTree(_root, 0, blackcount);
}最长路径
int _maxHeight(Node* root)
{
if (root == nullptr)
return 0;
int lh = _maxHeight(root->_left);
int rh = _maxHeight(root->_right);
return lh > rh ? lh + 1 : rh + 1;
}最短路径
int _minHeight(Node* root)
{
if (root == nullptr)
return 0;
int lh = _minHeight(root->_left);
int rh = _minHeight(root->_right);
return lh < rh ? lh + 1 : rh + 1;
}