1. 简介
堆(Heap)在计算机科学中可以表示内存的一部分,也是数据结构与算法中一种非常常用的数据结构。
尤其是在较大数据量的排序等问题中,堆排序经常被使用,因为堆排序的时间复杂度为 O(nlogn)。堆排序也是面试中经常被问到的对大量数据排序的算法,如海量数据选出 TOP K 等。
堆的结构
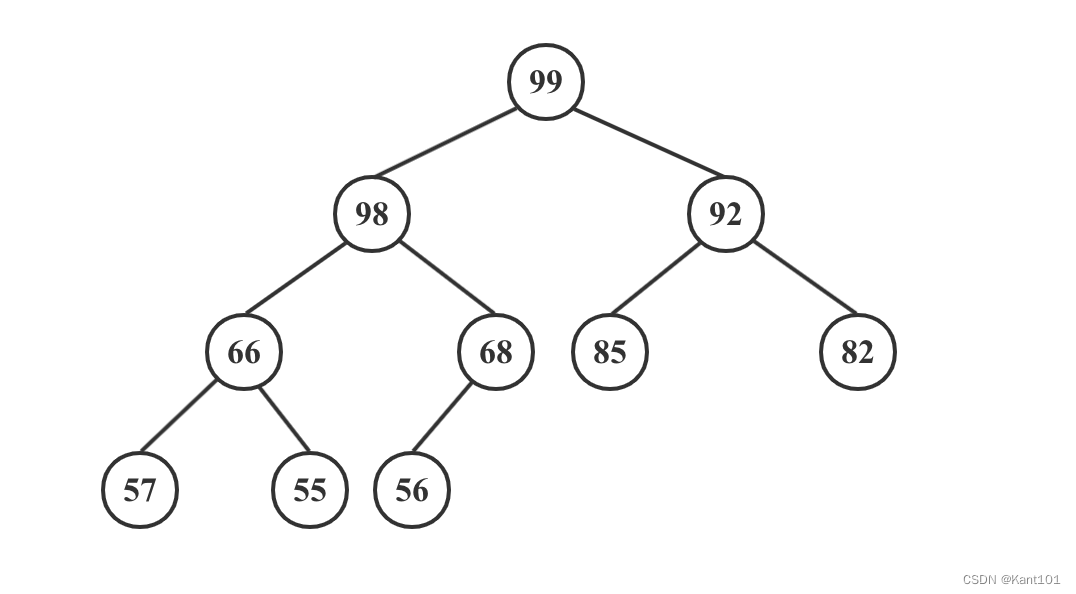
堆是一棵完全二叉树,且分为 大顶堆 和 小顶堆 两种结构:大顶堆中根结点的值大于左右子结点的值;小顶堆中根结点的值小于左右子结点的值。
大顶堆示例如下图所示:
2. 建堆和添加、删除操作
2.1 建堆
我们以如下所示的原始完全二叉树为例,详细描述大顶堆建堆的整过程。
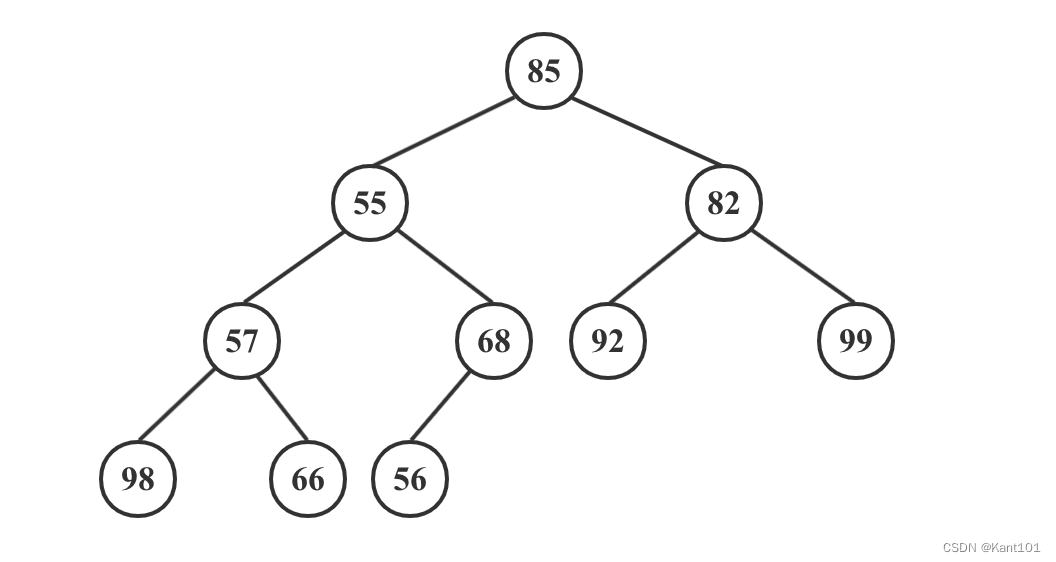
给定的数字的初始序列为: 85、55、82、57、68、92、99、98、66、56
将它们按照树的层序从上到下、从左到右依次摆放就得到如上图所示的初始的完全二叉树(堆是一种完全二叉树)
现在要调整这个初始堆,使它成为一个大顶堆。
调整的策略是:从最后一个结点开始从右向左、从下到上调增,使得父结点的值大于两个子结点的值。并且,对交换的子结点还要进行递归,使得它下面的子树仍然满足大顶堆的性质。
1)56比它的父结点68的值下,因此56不需要调整;
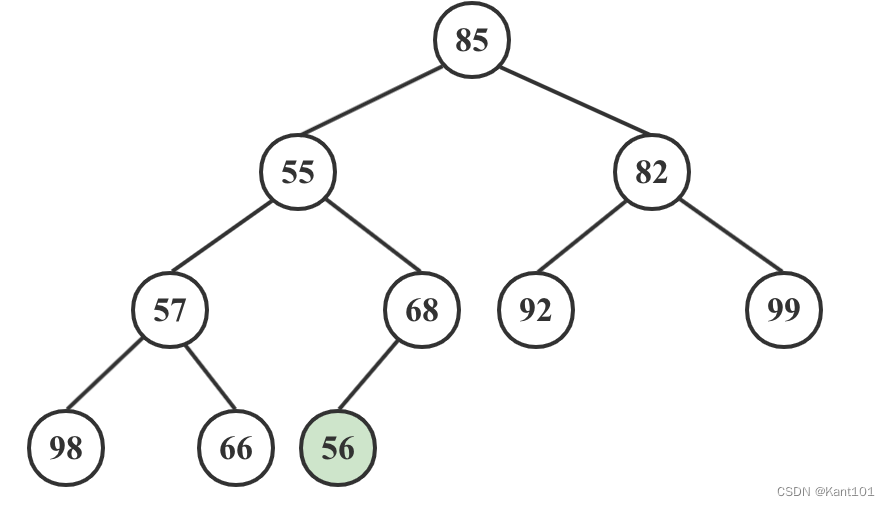
2)66和98两个子结点的值和它们的父结点相比较,选择最大的值做父结点,将原来的父结点的值与最大值的根结点交换,如下图:
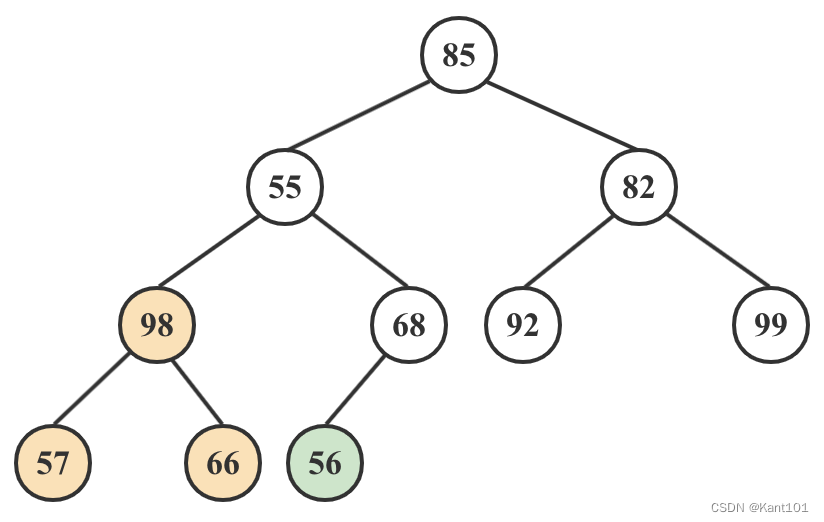
3)99和92与它们的父结点相比较,选择最大的做父结点,得到如下图
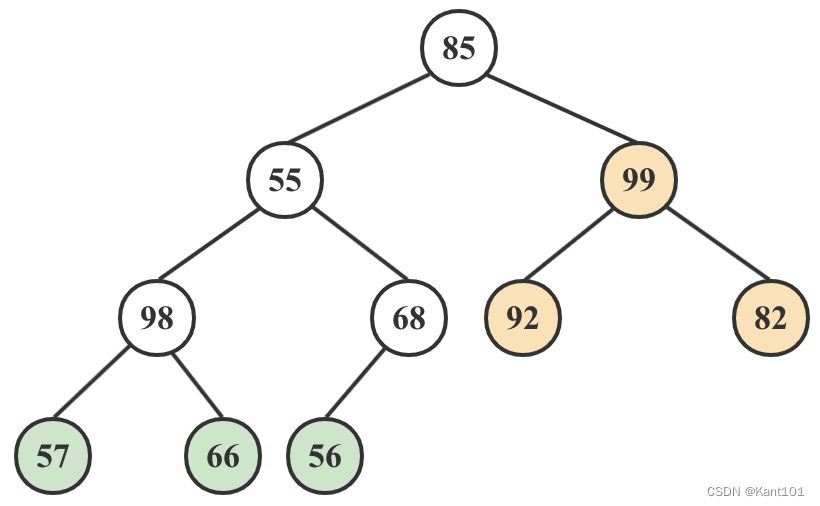
4)68和98与它们的父结点相比较,选择最大的98做父结点,即55和98交换。交换后还要对55进行递归,55比它的子结点小,继续调整,最终得到如下图:
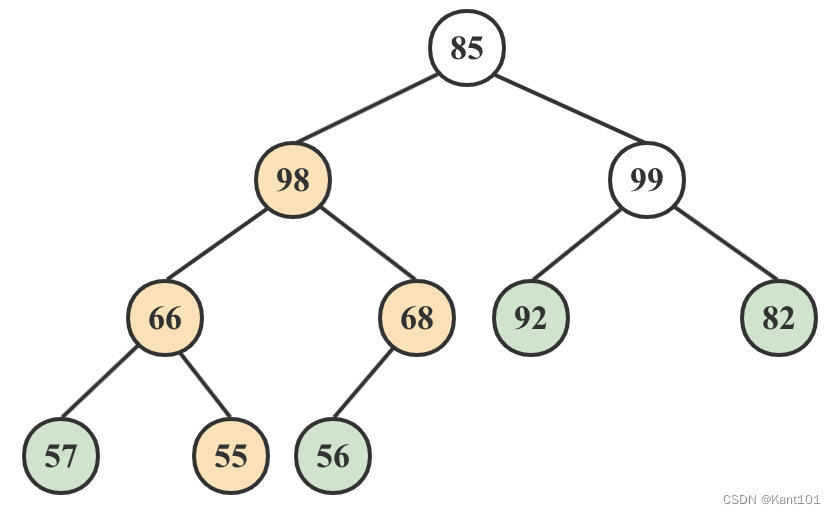
5)99和98与它们的父结点相比较,选择最大的99做父结点,即将85与99交换。交换后还需要对85递归,最终得到如下图:

最终,所有结点都进行了调整,得到了大顶堆如下:
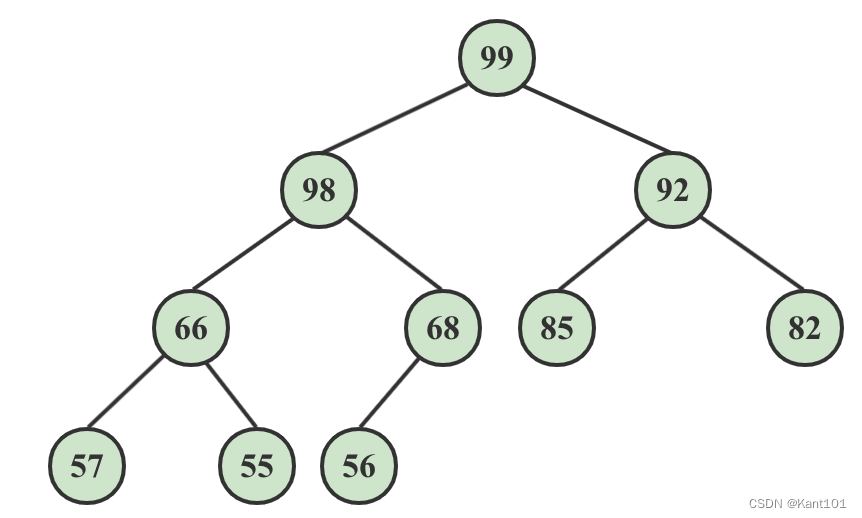
对树进行调整的代码
//heap为堆,n为元素个数,heap数组有效数字下标要从1开始
vector<int> heap;
// 元素个数
int size;
/**
* 对 heap 数组在 [low, high] 范围进行向下调整
* 其中low为欲调整结点的下标,high一般为堆的最后一个元素的数组下标
*/
void downAdjust(int low, int high) {
int i = low, j = i * 2; // i为欲调整结点,j为其左孩子
while (j <= high) { //存在孩子结点
// 如果右孩子存在,且右孩子的值大于左孩子
if (j + 1 <= high && heap[j + 1] > heap[j]) {
j = j + 1; // 让j存储右孩子下标
}
// 如果孩子中最大的权值比欲调整结点i大
if (heap[j] > heap[i]) {
swap(heap[i], heap[j]); // 交换最大权值的孩子与欲调整结点i
i = j; //保持i为欲调整结点,j为其左孩子
j = i * 2;
} else {
break; // 孩子的权值均比欲调整结点i小,调整结束
}
}
}
heap 数组下标的范围为 1~n。完全二叉树的叶子结点个数为 ?n/2?,因此数组下标在 [1, ?n/2? 范围内的结点都是非叶子结点。于是可以从 ?n/2? 号位开始倒着枚举结点,对每个遍历到的结点i进行 [i, n] 范围的调整。
建堆代码
// 建堆
void createHeap() {
for (int i = n / 2; i >= 1; i--) {
downAdjust(i, n);
}
}
2.2 删除堆顶元素操作
如果要删除堆中的最大元素(也就是删除堆顶元素),并且让其仍然保持堆的结构,那么只需要最后一个元素覆盖堆顶元素,然后对根结点进行调整即可。时间复杂度为 O(logn) .
// 删除堆顶元素
int deleteTop() {
int res = heap[1];
heap[1] = heap[size--];
heap.pop_back();
downAdjust(1, size);
return res;
}
2.3 添加元素操作
添加元素操作:可以把要被添加的元素放在数组最后(也就是完全二叉树最后一个结点的后面),然后向上进行调整操作。
向上调整操作:总是把欲调整结点与父结点比较,如果权值比父结点大,那么就交换其与父结点,止痒反复比较,直到堆顶或者父结点的权值较大为止。时间复杂度为 O(logn) .
// 对heap数组在[low, high] 范围进行向上调整
// 其中low一般设置为1,high表示欲调整结点的数组下标
void upAdjust(int low, int high) {
int i = high, j = i / 2; // i为欲调整结点,j为其父结点
while (j >= low) { // 父结点在 [low, high] 范围内
// 父亲权值小于欲调整结点i的权值
if (heap[i] > heap[j]) {
swap(heap[i], heap[j]); // 交换父结点和欲调整结点
i = j; // 保持i为欲调整结点,j为其父结点
j = i / 2;
} else {
break; // 父亲权值比欲调整结点i的权值大,调整结束
}
}
}
// 添加元素x
void insert(int x) {
heap.push_back(x); // 让元素个数加1,然后将数组末位赋值为x
size++;
upAdjust(1, size); // 向上调整新加入的结点x
}
3. 堆排序
堆排序是使用堆结构对一个序列进行排序。
思路:堆顶元素是最大的,因此可以考虑取出堆顶元素,然后将堆的最后一个元素替换至堆顶,再进行一次针对堆顶元素的向下调整。如此重复,直到堆中只剩下一个元素为止。
// 堆排序
void heapSort() {
createHeap(); // 建堆
for (int i = n; i >= 1; i--) { //倒着枚举,直到堆中只有一个元素
swap(heap[i], heap[1]); // 交换heap[i]与堆顶
downAdjust(1, i - 1); // 调整堆顶
}
}
4. 测试
C++
#include <iostream>
#include <vector>
using namespace std;
class HeapSort {
public:
vector<int> heap; // 存储元素
int size; // 元素个数
HeapSort(vector<int> &nums) {
size = (int) nums.size();
heap.push_back(-1); // 堆中为便于计算父子结点关系,数组下标需要从1开始
for (int i = 0; i < size; i++) {
heap.push_back(nums[i]);
}
}
void downAdjust(int low, int high) {
int i = low, j = i * 2;
while (j <= high) {
if (j + 1 <= high && heap[j + 1] > heap[j]) {
j = j + 1;
}
if (heap[j] > heap[i]) {
swap(heap[i], heap[j]);
i = j;
j = i * 2;
} else {
break;
}
}
}
void createHeap() {
for (int i = size / 2; i >= 1; i--) {
downAdjust(i, size);
}
}
int deleteTop() {
int res = heap[1];
heap[1] = heap[size--];
heap.pop_back();
downAdjust(1, size);
return res;
}
void upAdjust(int low, int high) {
int i = high, j = i / 2;
while (j >= low) {
if (heap[i] > heap[j]) {
swap(heap[i], heap[j]);
i = j;
j = i / 2;
} else {
break;
}
}
}
void insert(int x) {
heap.push_back(x);
size++;
upAdjust(1, size);
}
void heapSort() {
createHeap();
for (int i = size; i >= 1; i--) {
swap(heap[i], heap[1]);
downAdjust(1, i - 1);
}
}
};
int main() {
vector<int> nums = {9, 7, 5, 3, 1, 2, 4, 6, 8};
HeapSort heapSort(nums);
// 打印出元素序列
for (int i = 1; i <= heapSort.size; i++) {
cout << heapSort.heap[i] << " ";
}
cout << endl;
// 建堆
heapSort.createHeap();
// 删除堆顶元素,被删除的应为9
int res = heapSort.deleteTop();
cout << "top element: " << res << endl;
// 接着删除堆顶元素,被删除的应为8
res = heapSort.deleteTop();
cout << "top element: " << res << endl;
// 接着删除堆顶元素,被删除的应为7
res = heapSort.deleteTop();
cout << "top element: " << res << endl;
// 向堆中插入新元素-8
heapSort.insert(-8);
// 向堆中插入新元素-2
heapSort.insert(-2);
// 对堆中剩余元素进行堆排序
heapSort.heapSort();
// 打印出堆排序后的元素序列
for (int i = 1; i <= heapSort.size; i++) {
cout << heapSort.heap[i] << " ";
}
return 0;
}
测试结果
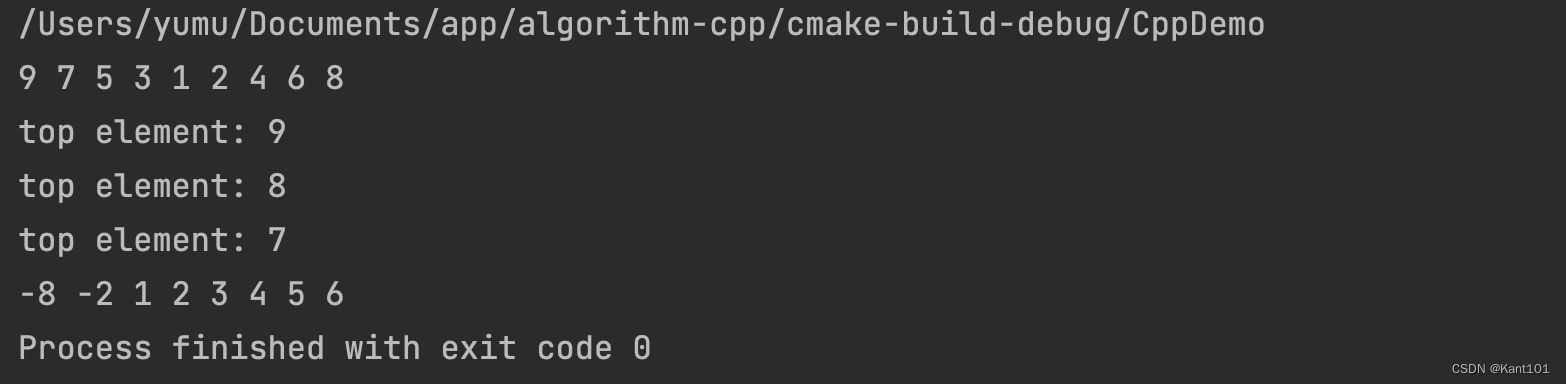
JAVA
/**
* @date 2022/8/15
*/
public class HeapSort {
/**
* 存储数据
*/
private int[] heap;
/**
* 堆元素个数
*/
private int size;
public HeapSort(int[] nums) {
size = nums.length;
heap = new int[size + 1];
for (int i = 0; i < nums.length; i++) {
heap[1 + i] = nums[i];
}
}
public void downAdjust(int low, int high) {
int i = low, j = i * 2;
while (j <= high) {
if (j + 1 <= high && heap[j + 1] > heap[j]) {
j = j + 1;
}
if (heap[j] > heap[i]) {
int tmp = heap[i]; // 交换i和j
heap[i] = heap[j];
heap[j] = tmp;
i = j;
j = i * 2;
} else {
break;
}
}
}
public void createHeap() {
for (int i = size / 2; i >= 1; i--) {
downAdjust(i, size);
}
}
public int deleteTop() {
int res = heap[1];
heap[1] = heap[size--];
downAdjust(1, size);
return res;
}
public void upAdjust(int low, int high) {
int i = high, j = i / 2;
while (j >= low) {
if (heap[i] > heap[j]) {
int tmp = heap[i]; // 交换heap[i]和heap[j]
heap[i] = heap[j];
heap[j] = tmp;
i = j;
j = i / 2;
} else {
break;
}
}
}
public void insert(int x) {
if (size + 1 >= heap.length) {
int[] newHeap = new int[size * 2];
System.arraycopy(heap, 0, newHeap, 0, size);
heap = newHeap;
}
heap[++size] = x;
upAdjust(1, size);
}
public void heapSort() {
for (int i = size; i >= 1; i--) {
int tmp = heap[1];
heap[1] = heap[i];
heap[i] = tmp;
downAdjust(1, i - 1);
}
}
// 打印heap数组元素,测试用
public void printHeap() {
for (int i = 1; i <= size; i++) {
System.out.print(heap[i] + " ");
}
System.out.println();
}
public static void main(String[] args) {
int[] nums = {9, 7, 5, 3, 1, 2, 4, 6, 8};
HeapSort heapSort = new HeapSort(nums);
// 打印出元素序列
heapSort.printHeap();
// 建堆
heapSort.createHeap();
// 删除堆顶元素,被删除的应为9
int res = heapSort.deleteTop();
System.out.println("top element: " + res);
// 接着删除堆顶元素,被删除的应为8
res = heapSort.deleteTop();
System.out.println("top element: " + res);
// 接着删除堆顶元素,被删除的应为7
res = heapSort.deleteTop();
System.out.println("top element: " + res);
// 向堆中插入新元素-8
heapSort.insert(-8);
// 向堆中插入新元素-2
heapSort.insert(-2);
// 对堆中剩余元素进行堆排序
heapSort.heapSort();
// 打印出堆排序后的元素序列
heapSort.printHeap();
}
}
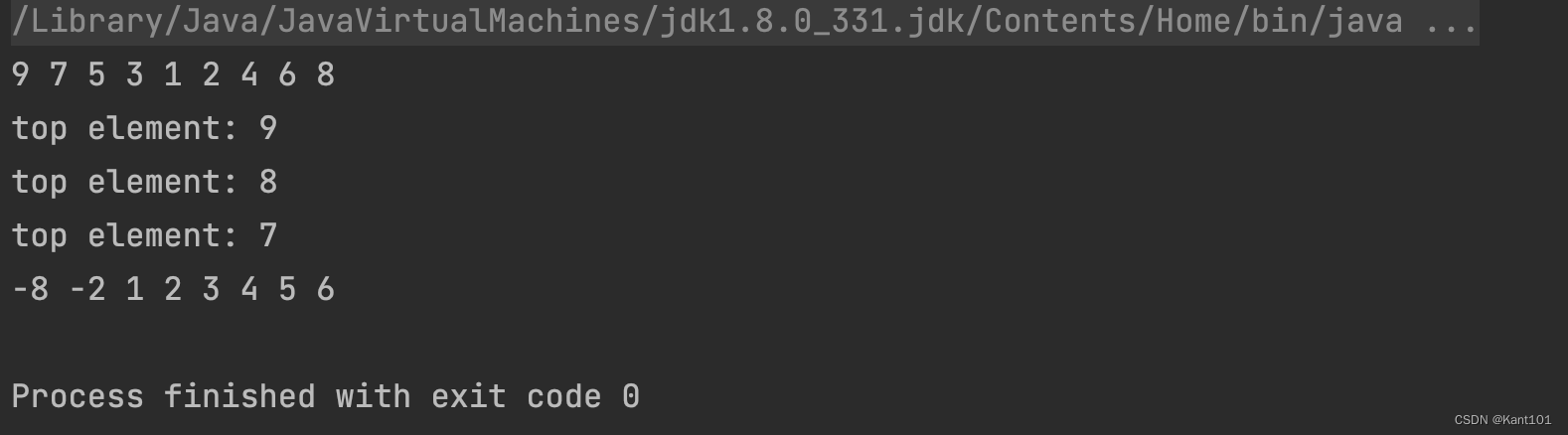
测试结果
5. TOP K 问题
TOP K问题是面试中常常被问到的问题,从大量的数据中,找出最小的或者最大的几个值,这就可以采用 堆 来实现。
例如,给定1,000,000个整数,要求从中找出最大的10个数。
我们可以首先用前10个数建立一个size为10的 小顶堆,即堆顶元素是10个数中最小的。然后依次取出后面的10 ~ 1,000,000个数,将其与小顶堆的堆顶元素进行比较:
- 如果小于等于堆顶元素,则说明这个数比堆中的10个元素都小,跳过;
- 如果大于堆顶元素,则用该数替换掉小顶堆的堆顶元素,然后对小顶堆从堆顶向下做一次调整,使得还是形成小顶堆。
这样,当所有的数都验证完后,小顶堆中的10个元素就是这1,000,000个元素中最大的10个元素。
并且,当数据量非常大,内存无法一次性载入时仍然可以使用堆来获取 TOP K,将硬盘中的数据分块的载入内存,再与堆顶元素进行比较、替换、调整。
参考文献
《算法笔记》,胡凡、曾磊等.