目录
一、概念
Hash表:Hash表又称散列表,一般由Hash函数(散列函数)与链表结构共同实现。当我们要对若干复杂信息进行统计时,可以用Hash函数把这些复杂信息映射到一个容易维护的值域内,因为值域变简单、范围变小,有可能造成两种不同的原始信息被Hash函数映射为相同的值,所以我们会采用一些方案来解决这种冲突情况。
字符串Hash:字符串Hash采用特殊的Hash函数把一个任意长度的字符串映射成一个非负整数,并且其冲突概率几乎为零。其Hash函数取一固定值P,把字符串看做P进制数,并且分配一个大于0的数值,代表某种字符,然后取一固定值M,求出该P进制对M的余数,作为该字符串的Hash值。(p常取131或13331,此时Hash值产生冲突的概率极低,M常取2的64次方)
二、图示说明
1.Hash表
a.开散列法
开散列法:建立一个邻接表结构,以Hash函数的值域作为表头数组head,映射后的值相同的原始信息被分到同一类,构成一个链表接在对应的表头之后,链表的节点上可以保存原始信息和一些统计数据。
存储结构如图1所示

b.开放寻址法
开放寻址法:建立一个比存入数据量大两倍或三倍的存储空间,以hash函数映射后的值为起点寻找未存储数据的空间或者找到一个空间中存储的数据与要存储的数据相等时停止,然后将输入数据存入。
存储结构如图2所示

2.字符串Hash
字符串Hash,可以将一个任意长度的字符串映射成一个非负整数,映射方法为由第一个字符开始,到最后一个字符,每次累加一个字符到字符串的hash值,则当前字符串的hash值等于当前字符串没累加字符前的hash值乘上P,在加上累加字符的值。
如图3所示

?
三、操作说明
1.Hash表
a.开散列法
a1.插入数据
以图4,图5,图6为例,将2加入到hash表中。其中Hash函数为H(x)=((x mod p)+p) mod p(p为一个比较大的质数,图示中p为1e5+3)。先将2带入hash函数中映射得2,然后再将2插入head数组下标2做头结点的链表中。


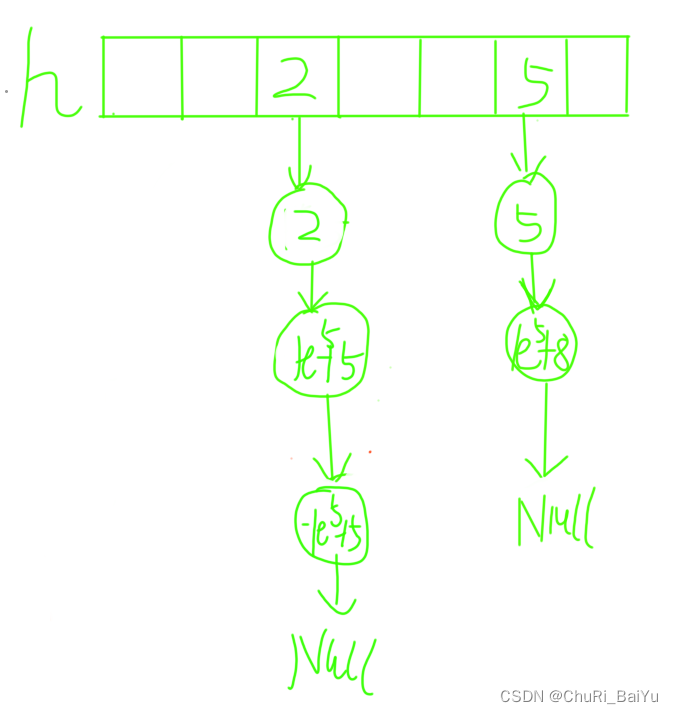
?????????
int head[N];///建立以0~N-1映射值为下标的头结点
int e[N]; ///存储原始值
int ne[N]; ///存储下一结点
int idx; ///结点编号
int n;
void insert(int x){
int k=(x%N+N)%N; ///将x映射至0~N-1中的k
e[idx]=x; ///存入原始数据x
ne[idx]=head[k]; ///新结点指向以映射值k为下标的head[k]为头结点所指向的结点
head[k]=idx; ///以映射值k为下标的head[k]做头结点指向新结点
idx++; ///结点编号后移
}
memset(head,-1,sizeof head); ///初始化每个链表的头结点
scanf("%d",&x);
insert(x);a2.查找数据
bool find(int x){
int k=(x%N+N)%N; ///将x映射至0~N-1中的k
///由以映射值k为下标的头结点开始遍历链表,寻找x
for(int i=head[k];i!=-1;i=ne[i]){
if(e[i]==x) return true;
}
return false;
}
cin >>x;
if(find(x)) puts("Yes");
else puts("No");b.开放寻址法
b1.插入数据
如图7,8,9,10所示 ,插入元素2e5+5。此时hash函数mod的质数为2e5+3,2e5+5的映射值为2,从2开始遍历,发现下标为2的位置已经存储了数据,且该数据不为2e5+5,故由该位置向后移动,发现移动后的位置未存储数据,故将2e5+5存入其中。
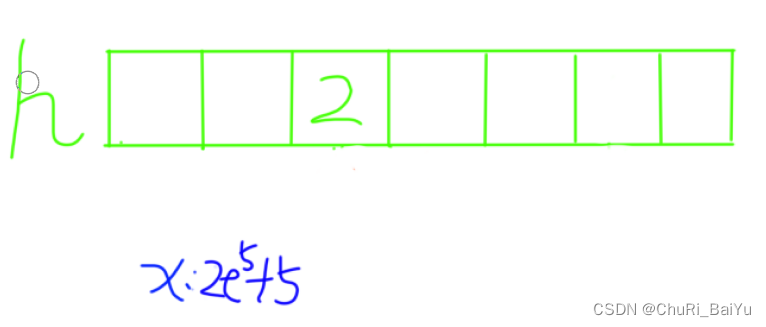
?????
??

???????
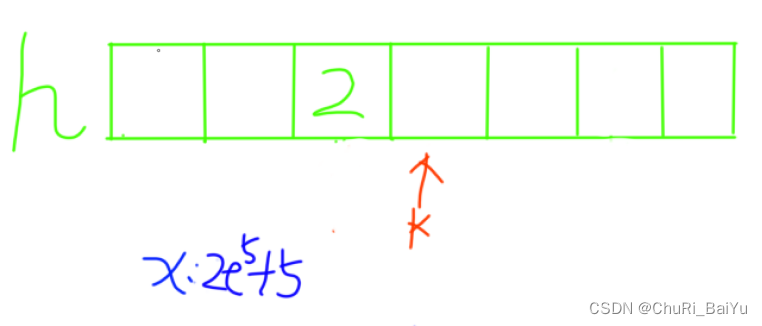

??
const int N=2e5+3,Null=0x3f3f3f3f;
int h[N], n;
int find(int x){
int k=(x%N+N)%N; ///将x映射至0~N-1中的k
///若当前位置被占据,且占据的数据不等于x时,继续寻找位置
while(h[k]!=Null&&h[k]!=x){
k++;
if(k==N) k=0; ///若当前位置到了数组的右边界,则重置寻找的位置
}
return k; ///返回寻找到的位置
}
///先将h中的每一个位置都进行初始化,以便检验是否存储数据
memset(h,Null,sizeof h);
scanf("%d",&x);
int k=find(x);
h[k]=x; ///将x存入找到的位置b2.查找数据
int find(int x){
int k=(x%N+N)%N; ///将x映射至0~N-1中的k
///若当前位置被占据,且占据的数据不等于x时,继续寻找位置
while(h[k]!=Null&&h[k]!=x){
k++;
if(k==N) k=0; ///若当前位置到了数组的右边界,则重置寻找的位置
}
return k; ///返回寻找到的位置
}
scanf("%d",&x);
int k=find(x);
///找到的位置k,要么时是个空位置可以存储x,要么是该位置已经存入x了
if(h[k]!=Null) puts("Yes");
else puts("No");2.字符串Hash
a.字符串预处理
如图11所示,预处理字符串"abcxyz"。由第一个字符开始,将每一个字符逐渐累加,每一个累加字符后的字符串等于累加字符前的字符串的hash值乘上P再加上当前字符的值。

?
typedef unsigned long long ULL; ///范围为0~2^64,溢出自动取模
const int N=1e5+10,P=131;
ULL h[N],p[N]; ///h[]存储hash值,p[]存储p的i次幂,且数据类型为ULL,溢出自动取模
char str[N];
int n,m;
scanf("%d%s",&n,str+1);
p[0]=1; ///P的0次幂等于1
for(int i=1;i<=n;i++){ ///预处理长度为n的字符串
p[i]=p[i-1]*P; ///P的次幂预处理
h[i]=h[i-1]*P+str[i]; ///处理1~i字符的hash值
}b.字符子串查询
如图12,查询字符串中字符4~字符6组成字符的hash值。操作是,将区间右端点中存储的hash值,减去区间左端点-1的hash值乘上P的区间右端点减区间左端点-1次幂的值。

?
ULL get(int l,int r){
///将区间右端点中存储的hash值,减去区间左端点-1的hash值乘上P的区间右端点减区间左端点-1次幂的值。
return h[r]-h[l-1]*p[r-l+1];
}
scanf("%d%d",&l1,&r1);
cout <<get(l1,r1) <<endl;
四、例题实战
1.hash表
a.题目描述
维护一个集合,支持如下几种操作:
I x,插入一个数?x;Q x,询问数?x?是否在集合中出现过;
现在要进行?N?次操作,对于每个询问操作输出对应的结果。
输入格式
第一行包含整数?N,表示操作数量。
接下来?N?行,每行包含一个操作指令,操作指令为?I x,Q x?中的一种。
输出格式
对于每个询问指令?Q x,输出一个询问结果,如果?x?在集合中出现过,则输出?Yes,否则输出?No。
每个结果占一行。
数据范围
1≤N≤1e5
?1e9≤x≤1e9
输入样例:
5
I 1
I 2
I 3
Q 2
Q 5
输出样例:
Yes
Nob.解题思路
思路:使用hash表存储查询数据
c.代码实现
```
///开放寻址法
#include<iostream>
#include<cstring>
using namespace std;
const int N=2e5+3,Null=0x3f3f3f3f;
int h[N], n;
int find(int x){
int k=(x%N+N)%N; ///将x映射至0~N-1中的k
///若当前位置被占据,且占据的数据不等于x时,继续寻找位置
while(h[k]!=Null&&h[k]!=x){
k++;
if(k==N) k=0; ///若当前位置到了数组的右边界,则重置寻找的位置
}
return k; ///返回寻找到的位置
}
int main(){
cin >>n;
int x;
///先将h中的每一个位置都进行初始化,以便检验是否存储数据
memset(h,Null,sizeof h);
while(n--){
char op[2];
scanf("%s%d",op,&x);
int k=find(x);
if(op[0]=='I'){
h[k]=x; ///将x存入找到的位置
}
else{
///找到的位置k,要么时是个空位置可以存储x,要么是该位置已经存入x了
if(h[k]!=Null) puts("Yes");
else puts("No");
}
}
return 0;
}
```
```
///开散列法
#include<iostream>
#include<cstring>
using namespace std;
const int N=1e5+3;
int head[N];///建立以0~N-1映射值为下标的头结点
int e[N]; ///存储原始值
int ne[N]; ///存储下一结点
int idx; ///结点编号
int n;
void insert(int x){
int k=(x%N+N)%N; ///将x映射至0~N-1中的k
e[idx]=x; ///存入原始数据x
ne[idx]=head[k]; ///新结点指向以映射值k为下标的head[k]为头结点所指向的结点
head[k]=idx; ///以映射值k为下标的head[k]做头结点指向新结点
idx++; ///结点编号后移
}
bool find(int x){
int k=(x%N+N)%N; ///将x映射至0~N-1中的k
///由以映射值k为下标的头结点开始遍历链表,寻找x
for(int i=head[k];i!=-1;i=ne[i]){
if(e[i]==x) return true;
}
return false;
}
int main(){
cin >>n;
int x;
memset(head,-1,sizeof head); ///初始化每个链表的头结点
while(n--){
char op[2];
scanf("%s%d",op,&x);
if(op[0]=='I'){
insert(x);
}
else{
if(find(x)) puts("Yes");
else puts("No");
}
}
return 0;
}
```
2.字符串hash
a.题目描述
给定一个长度为?n?的字符串,再给定?m?个询问,每个询问包含四个整数 l1,r1,l2,r2,请你判断?[l1,r1]和?[l2,r2]?这两个区间所包含的字符串子串是否完全相同。
字符串中只包含大小写英文字母和数字。
输入格式
第一行包含整数?n?和?m,表示字符串长度和询问次数。
第二行包含一个长度为?n?的字符串,字符串中只包含大小写英文字母和数字。
接下来?m?行,每行包含四个整数?l1,r1,l2,r2,表示一次询问所涉及的两个区间。
注意,字符串的位置从?1?开始编号。
输出格式
对于每个询问输出一个结果,如果两个字符串子串完全相同则输出?Yes,否则输出?No。
每个结果占一行。
数据范围
1≤n,m≤1e5
输入样例:
8 3
aabbaabb
1 3 5 7
1 3 6 8
1 2 1 2
输出样例:
Yes
No
Yesb.解题思路
思路:使用字符串hash的方法将该字符串存入h[]中,然后输入两区间,查询两个区间的hash值是否相等。
c.代码实现
#include<iostream>
#include<cstdio>
using namespace std;
typedef unsigned long long ULL; ///范围为0~2^64,溢出自动取模
const int N=1e5+10,P=131;
ULL h[N],p[N]; ///h[]存储hash值,p[]存储p的i次幂,且数据类型为ULL,溢出自动取模
char str[N];
ULL get(int l,int r){
///将区间右端点中存储的hash值,减去区间左端点-1的hash值乘上P的区间右端点减区间左端点-1次幂的值。
return h[r]-h[l-1]*p[r-l+1];
}
int main(){
int n,m;
scanf("%d%d%s",&n,&m,str+1); ///字符串由下标1开始存储
p[0]=1; ///P的0次幂等于1
for(int i=1;i<=n;i++){ ///预处理长度为n的字符串
p[i]=p[i-1]*P; ///P的次幂预处理
h[i]=h[i-1]*P+str[i]; ///处理1~i字符的hash值
}
while(m--){
int l1,r1,l2,r2;
scanf("%d%d%d%d",&l1,&r1,&l2,&r2);
if(get(l1,r1)!=get(l2,r2)) puts("No");
else puts("Yes");
}
return 0;
}