🥳知识导航
一.维护红黑树的五条性质
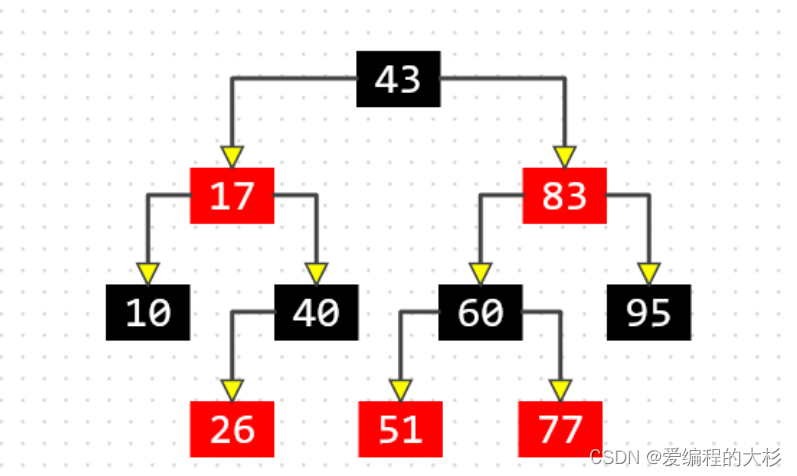
红黑树与AVL树一样都是一颗自平衡二叉树，都能自主达到平衡。AVL树的平衡是判断左右子树的高度差的绝对值是否小于1.而红黑树的平衡只需保证它的以下几个性质达到满足即可：
1.节点是RED或者BLACK
2.根节点是BLACK节点
3.不能出现连续两个红色节点（可以出现连续两个黑色节点）
4.RED节点的子节点和父节点都是BLACK
5. 从任一节点到叶子节点的所有路径都包含相同数目的 BLACK 节点
6.叶子节点都是BLACK,(问上图叶子节点看着不全是黑色？答：这里所说的黑色节点是假想的黑色节点)
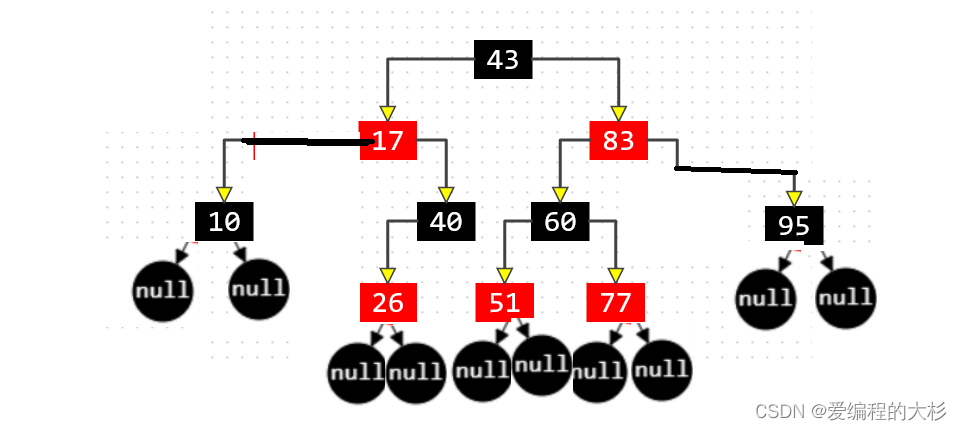
上面这几个性质不难理解，那么有人问了，为什么满足这几个性质就一定是平衡的？
从b树角度便可以很容易理解这个问题，因为红黑树等价于四阶b树，满足那几个性质的树就是一个红黑树，等价于四阶b树，b树一定是平衡的。
二、红黑树与四阶b树的等价变换
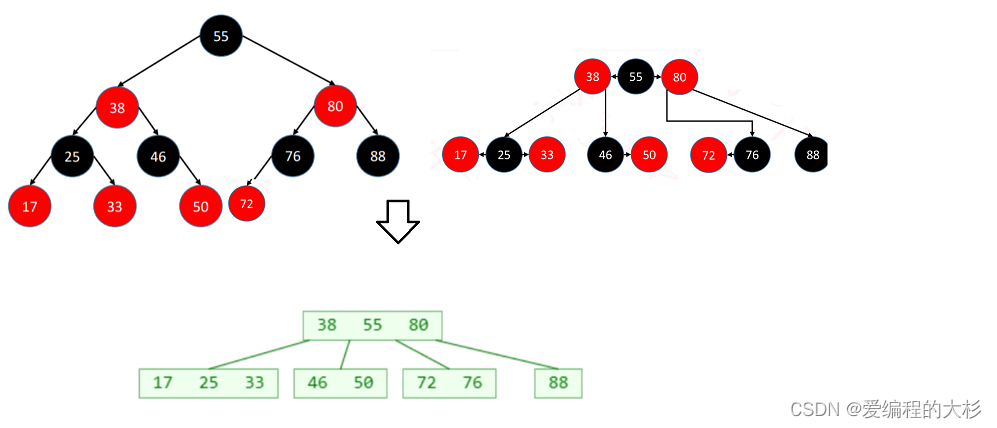
1.黑色节点与它的红色子节点合并看成一个b树节点，红黑树就类比转化成为了一颗b树。
2.红黑树的 BLACK 节点个数 与 4阶B树的节点总个数 相等
三.简单的继承关系
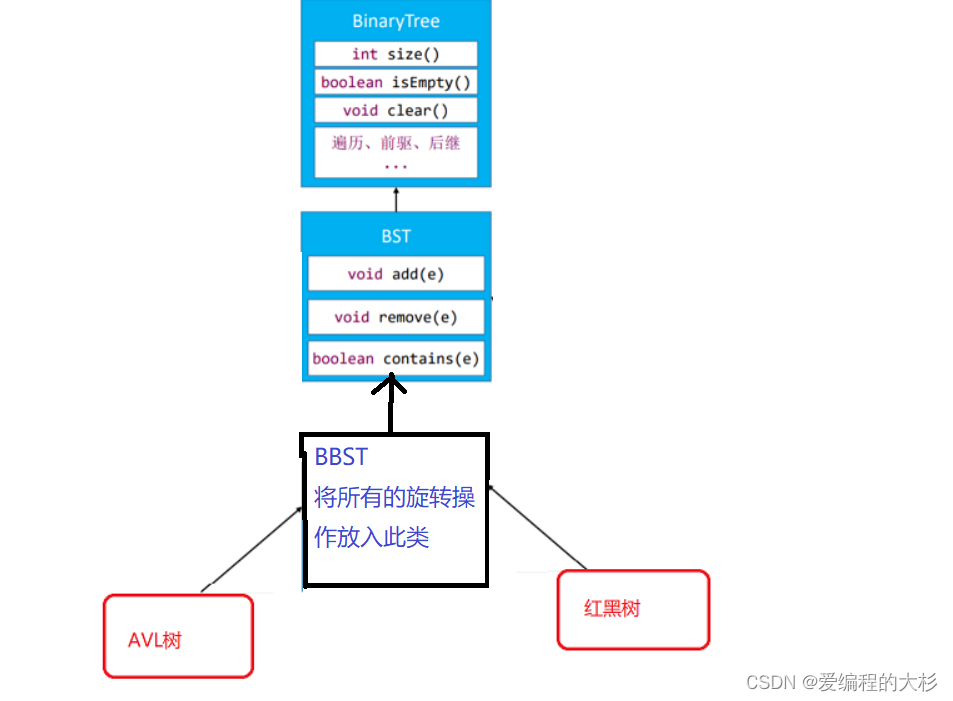
具体代码细节可移步代码仓库—>代码仓库
四.重新定义红黑树节点
理清亲子关系
//自定义内部类-->红黑树类型
public static class RBNode<E>extends Node<E>{
boolean color=RED;
//为什么默认为红色：因为默认为红色的情况下对于红黑树的几个条件除了
//出现连续红色节点可能不满足，其余条件都满足，所以更加的适合将红色设置为默认颜色
//更容易使红黑树的性质得到满足
//4不满足的可能情况使出现两个连续的红色子节点
public RBNode(E element, Node<E> parent) {
super(element, parent);
}
//内部类重新定义一个方法--->返回兄弟节点
//不用定义返回叔父节点-->因为node.parent.sibling()-->就是叔父节点
public Node<E> sibling()
{
if(isLeftChild())
{
return parent.right;
}
if(isRightChild()){
return parent.left;
}
return null;
}
@Override
public String toString() {
String str="";
if(color==RED){
str="R_";
}
return str+element.toString();
}
}
为什么默认为红色：因为默认为红色的情况下对于红黑树的几个条件除了出现连续红色节点可能不满足，其余条件都满足，所以更加的适合将红色设置为默认颜色.
因为默认为红色节点，并且要规避连续两个红色的情况.所以添加的时候需要对所有可能添加的位置进行分类，添加节点的父节点为黑色时无需处理直接添加即可，如果添加节点的父节点是红色，则应该按情况处理双红的局面
四.红黑树添加后的调整
有 4 种情况满足红黑树的性质 4 ：parent 为 BLACK
同样也满足 4阶B树 的性质
因此不用做任何额外处理
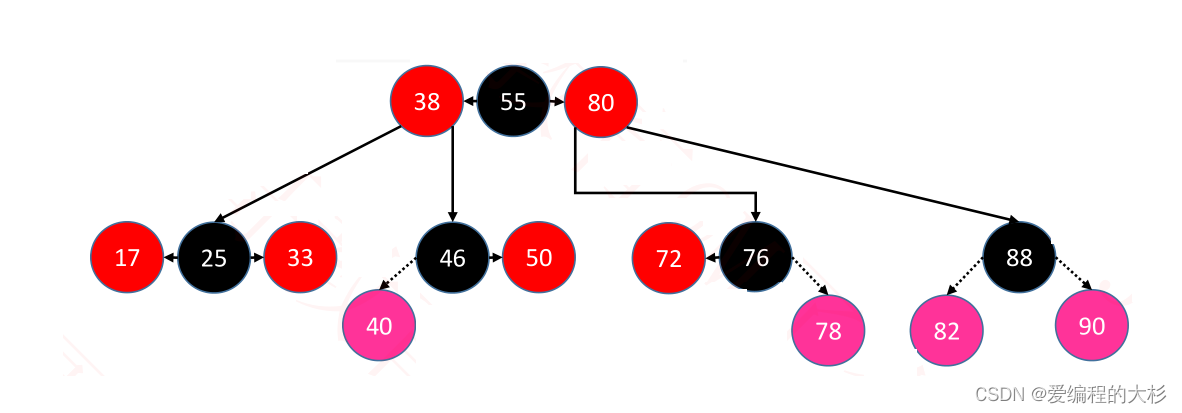剩余8个可以添加的位置，是不符合红黑树性质的—>会出现连续红色的现象.需要对其进行修复。这八种又分为两种，有四种会发生B树节点上溢的情况。
咱们先看不需要解决上溢的四种情况：🤩
1. 不会发生上溢 情况
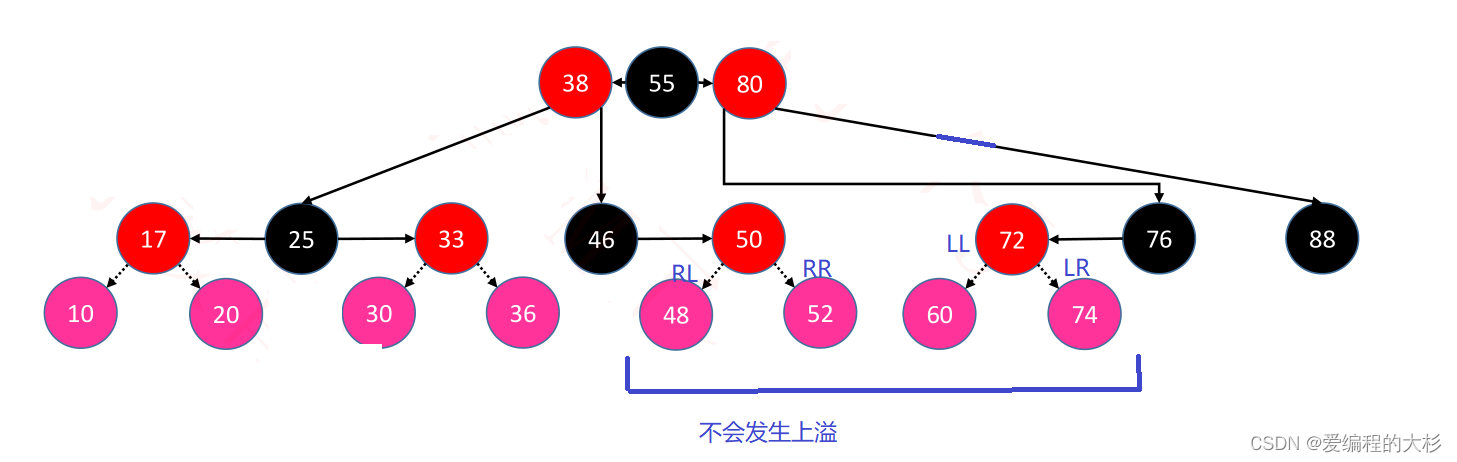
（1）LL与RR情况
解救方案：将parent染成黑色，grand染成红色，然后进行旋转（LL进行右旋转，RR进行左旋转）
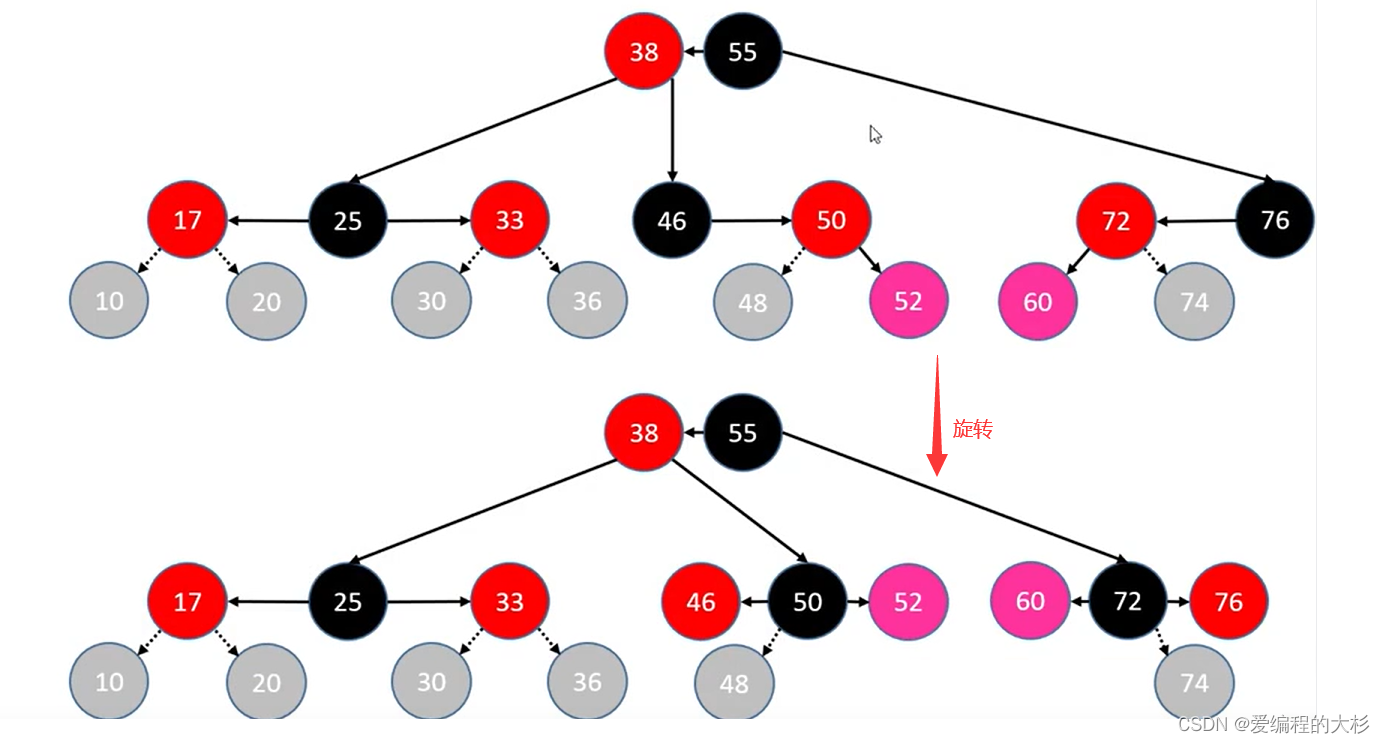
(2)LR与RL情况
- 自己染成 BLACK ，grand 染成 RED
- 进行双旋操作
3.LR：parent 左旋转， grand 右旋转
4.RL：parent 右旋转， grand 左旋转
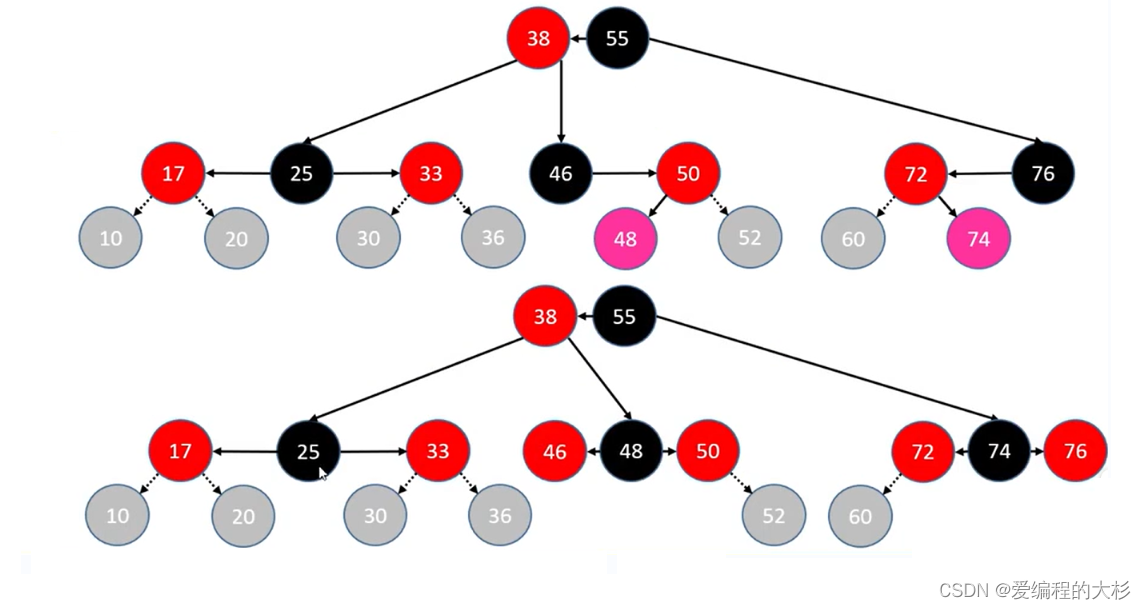
2. 会发生上溢情况
10为红色节点，肯定不会单独成为一颗子树，一定会向上合并，一旦合并，对于四阶B树节点，达到四个元素就会发生上溢，其余三种情况也是如此
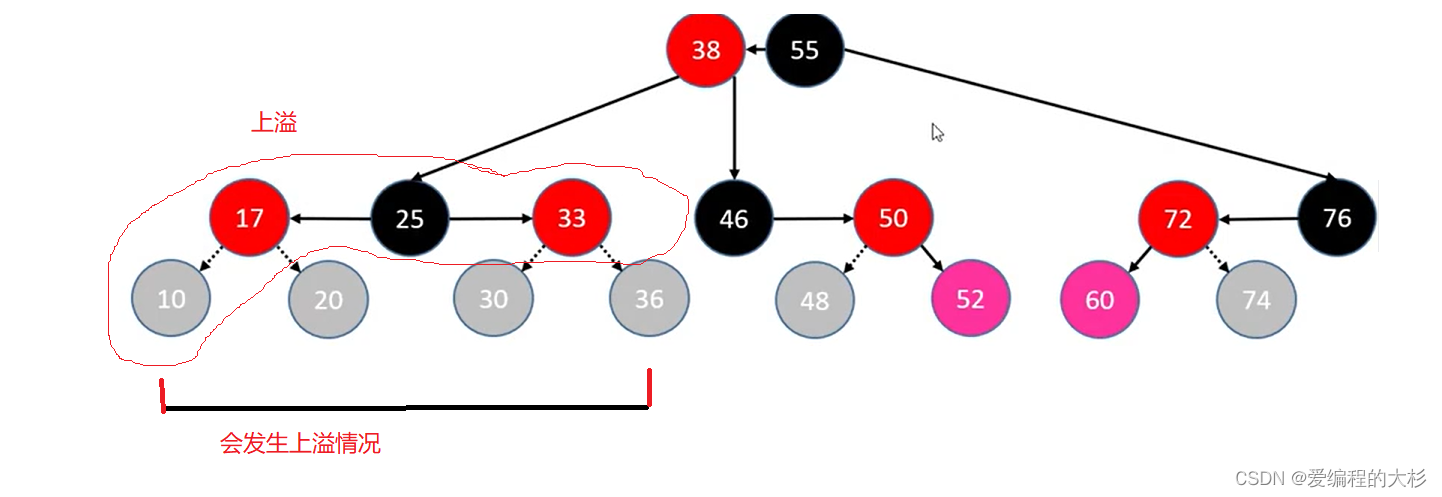
LL情况
类比上一节的B树，当B树节点发生上溢后的解决办法为
（找出节点的中间元素向上合并，然后中间元素两边元素分裂为两个子树。）
所以解决办法为，将parent,uncle节点染成黑色，grand节点染成红色，grand节点向上合并（当作新添加的节点，重复利用代码）。
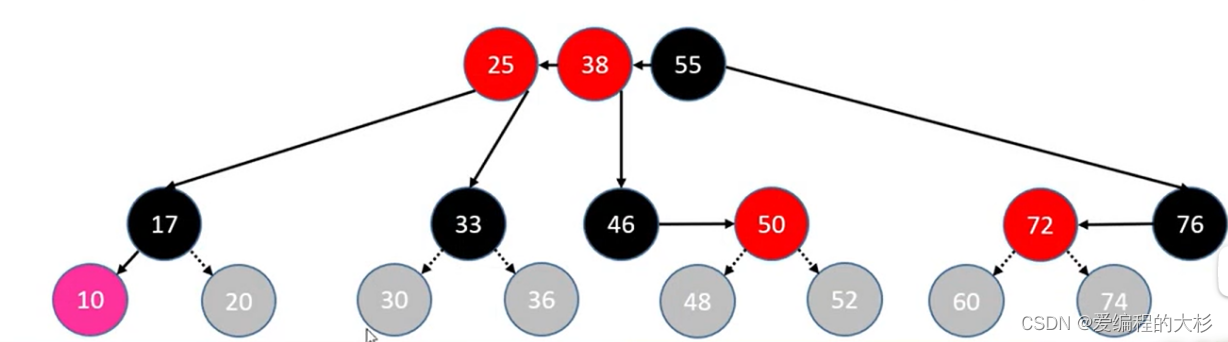? grand 向上合并时，可能继续发生上溢
? 若上溢持续到根节点，只需将根节点染成 BLACK
RR情况
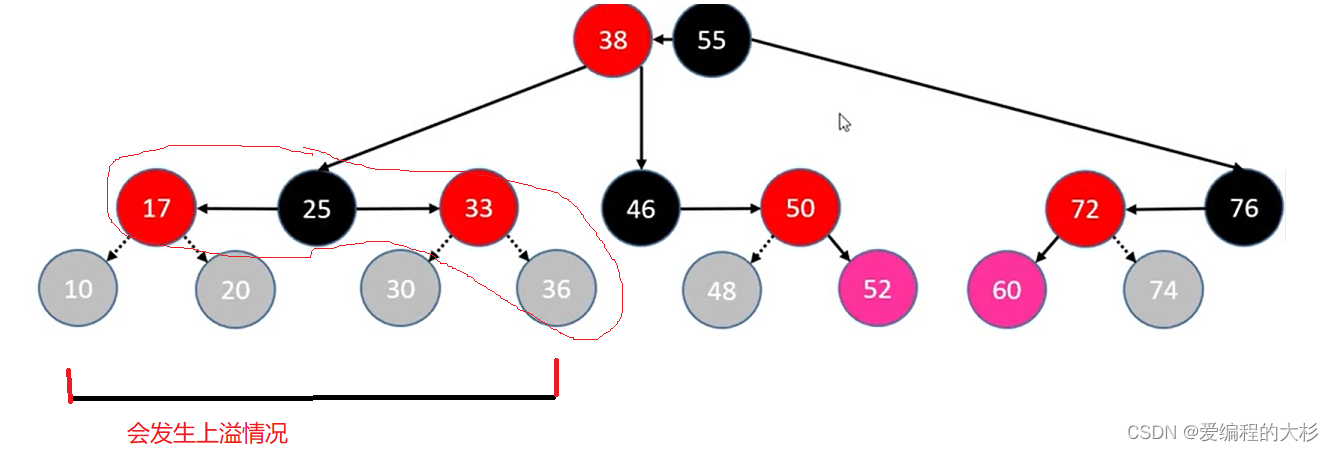
- parent、uncle 染成 BLACK
- grand 向上合并
- 染成 RED ，当做是新添加的节点进行处理
LR，RL情况
解决方法同上面一样
添加调整代码
/**
* 添加：如果第一次添加的是根节点，但是默认颜色为红色，所以需要将其染黑
*
* |-----红---黑---红
* | | | |
* 红---黑---红 黑--红 红--黑 黑
* 4 3 3 2
* 1.有四种情况直接满足红黑树的性质，父节点parent为黑节点--->不可能造成两个红节点连续的情况
* 2.其余八种父节点（parent）需要特殊处理---又按照叔父节点是红色和叔父节点是黑色划分，叔父节点是红色的会发生上溢
* 。但是叔父节点为黑色另有不同--->LL RR LR RL （grand进行单旋）
* @param node 新添加的节点->太秒了
*/
@Override
protected void afterAdd(Node<E> node) {
Node<E> parent=node.parent;
//这个代码块包括两种情况--->（1）第一次添加节点（2）叔父节点是红色的情况下，上溢到了根节点
if(parent==null){
black(node);
root=node;
return;
}
if(isBlack(parent))
{
//排除本身就满足条件的哪四种情况,不需要额外处理
return;
}
Node<E> uncle=parent.sibling();
Node<E> grand=parent.parent;
//叔父节点是红色-->发生上溢
if(isRed(uncle)){
//上溢分裂的情况
black(parent);
black(uncle);
//把祖父节点当成一个新添加的节点加到上面-->解决上溢
afterAdd(red(grand));
return;
}
//叔父节点不是红节点
if(parent.isLeftChild())
{
//由于染色顺序并不影响所以可以把统一的染色顺序放在前面red(grand)
//LL RR 单旋
if(node.isLeftChild()){//LL
black(parent);
red(grand);
}else {//LR
black(node);
red(grand);
rotateLeft(parent);
}
rotateRight(grand);
}else{
if(node.isRightChild())//RR
{
black(parent);
red(grand);
}else{//RL
black(node);
red(grand);
rotateRight(parent);
}
rotateLeft(grand);
}
}
五.四.红黑树删除后的调整
删除代码过繁杂，可以移步代码仓库的删除代码逻辑梳理图解–>gitee代码仓库
删除后调整代码
//删除黑色节点要传入黑色节点的替代节点
@Override
protected void afterRemove(Node<E> node, Node<E> replacement) {
//b树类比红黑树一定是删除的最后一层。如果要删除的是红色，由于黑色是主体，
// 所以要删除的节点一定度为0的红色叶子节点，不会影响原本红黑树的规则，所以不用调整，直接结束函数
if(isRed(node)){
return;
}
/**
* 一定要清楚afterRemove的作用是删除之后的调整，不是主体删除方法。
* 作用：对于不符合红黑树性质的操作及时进行调整
*
* 问：对于删除度为2的黑色节点，是不是可是囊括
* 答：可以：因为删除度为2的黑色节点，找到前驱后，还是删除红色节点不用处理，染黑替代节点并不影响，因为已经删除
*
* 为什么黑色节点的替代不能为黑色节点
* 因为b树的删除都是在最后一层进行操作，如果黑色节点子节点依然是一个黑色节点，由于黑色才是主体
* 不会融入到一个节点中，所以只会向下增高一层，不符合删除在最后一层操作。，
*/
if(isRed(replacement)){
//染黑：避免出现连续两个红色节点
black(replacement);
return;
}
/**
* 处理最后一种情况-->删除度为0的黑色叶子节点的调整方法
*
* 删除度为0的黑色叶子节点的调整方法肯定会造成下溢
* 补救:(1)看看兄弟节点能不能借
* a:兄弟节点能借的条件：1.兄弟节点是黑色 2.兄弟节点至少拥有一个红色子节点
* ----------------------------------------
* 能借后做出的操作：
* ?进行旋转操作
* ?旋转之后的中心节点继承 parent 的颜色
* ?旋转之后的左右节点染为 BLACK（因为此时红色子节点已经旋上去了）
*
* 旋转有三种情况：LL LR LL
*
* 🤩🤩特殊情况1：
* 如果被删除的是黑色，它的父节点也是黑色，删除后黑色父节点也会向下合并，造成父节点继续下溢
*只需将这个父节点当成一个新的被删除的黑色节点递归调用afterRemove方法，重复利用代码
*
* 🤩🤩特殊情况2：
* 🚩🚩🚩如果兄弟节点是红色，对于b树的性质，【黑色节点与其红色节点组成一个b树节点】
* 可知：红色节点一定在父节点中-->红色的节点的子节点一定是黑的，可以借侄子的【想办法将侄子变成兄弟】
* 强制将侄子变成兄弟再次套用兄弟节点是黑色是的代码
*-----------------------------------------------
*/
Node<E> parent=node.parent;
if(parent==null)
{
return;
}
//这么写有问题：node已经被删除--->指向node的线已经断了
//Node<E> sibling =node.sibling();
/**
* 需要间接求出兄弟节点
* 只需知道被删除的节点先前是在parent的左边还是右边，进而知道sibling是parent.left还是parent.right
*/
/**
* 为什么以此作为判定标准：
* 因为在二叉搜索树的删除中，删除黑色叶子节点,已经将一边置为null
* if (node == node.parent.left) {
* node.parent.left=null;
* } else { // node == node.parent.right
* node.parent.right=null;
* }
*/
//有特殊情况
boolean left=parent.left==null||node.isLeftChild();
Node<E> sibling=left?parent.right:parent.left;
if(left){//node是在左子树，兄弟节点在右边
if(isRed(sibling)){
black(parent);
red(sibling);
rotateLeft(parent);
//更新兄弟
sibling=parent.right;
}
//兄弟节点是黑色-->判断是否有红色子节点
//没有一个红色子节点--->父节点向下合并
/**
* 为什么以父节点是不是黑的为判定条件
* 因为如果父节点是红色，那它肯定不是主体，向下合并后，parent本身并没有下溢
* 如果父节点是黑色，那他向下合并后，自身也会下溢
*
*/
if(isBlack(sibling.left)&&isBlack(sibling.right)){
boolean parentBlack=isBlack(parent);
black(parent);
red(sibling);
//这种情况父节点向下合并，父节点的位置也会下溢
if(parentBlack){
//三黑局面没有替代节点
afterRemove(parent,null);
}
}else {//至少有一个红色子节点
//判断是LL LR.....
//三种情况:LL LR (LL或LR)
//可以先统一进行左旋转然后在统一进行右旋转
//如何区分LR左子节点是黑的
if(isBlack(sibling.left)) {//LR情况
rotateLeft(sibling);
//左旋转后兄弟节点已经发生了变化
sibling = parent.left;
}
//LL 情况
//现在的sibling已经更新过是图中的78
color(sibling,iscolor(parent));
black(parent);
black(sibling.left);
rotateRight(parent);
}
}else {//node是在右子树，兄弟节点在左边
//🤩🤩特殊情况2：
if(isRed(sibling)){
black(parent);
red(sibling);
rotateRight(parent);
//更新兄弟
sibling=parent.left;
}
//兄弟节点是黑色-->判断是否有红色子节点
//没有一个红色子节点--->父节点向下合并
/**
* 为什么以父节点是不是黑的为判定条件
* 因为如果父节点是红色，那它肯定不是主体，向下合并后，parent本身并没有下溢
* 如果父节点是黑色，那他向下合并后，自身也会下溢
*
*/
if(isBlack(sibling.left)&&isBlack(sibling.right)){
boolean parentBlack=isBlack(parent);
black(parent);
red(sibling);
//这种情况父节点向下合并，父节点的位置也会下溢
if(parentBlack){
//三黑局面没有替代节点
afterRemove(parent,null);
}
}else {//至少有一个红色子节点
//判断是LL LR.....
//三种情况:LL LR (LL或LR)
//可以先统一进行左旋转然后在统一进行右旋转
//如何区分LR左子节点是黑的
if(isBlack(sibling.left)) {//LR情况
rotateLeft(sibling);
//左旋转后兄弟节点已经发生了变化
sibling = parent.left;
}
//LL 情况
//现在的sibling已经更新过是图中的78
color(sibling,iscolor(parent));
black(parent);
black(sibling.left);
rotateRight(parent);
}
}
红黑树整体代码
package Tree;
import java.util.Comparator;
/**
* 回忆红黑树应该有哪些操作
* 1.染色（公众接口）（1）染红（2）染黑
* 2.旋转：在不是红黑树的时候调整
* 3.RBNode类。增加颜色属性-->不需要高度，因为红黑树和AVL树是两回事，没有平衡因子的概念
* 4.重写afterAdd()方法，afterRemove()方法
* ...............
* 注意：RB树相当于四阶b树，所以节点元素个数可以为[1,3],b树添加第一个元素后，下一个元素仍旧是添加到这个节点。
* b树的元素添加必须是叶子节点，第一次添加叶子节点就是根节点
*--------------------------------------------------------------------------------------
* 红黑树由五条性质定义
* 1.节点只有RED和BLACK两种
* 2.根节点必须是BLACK
* 3.叶子节点都是BLACK--->注意这里说的叶子节点说的是虚拟假想的空节点
* 4.RED子父节点都是BLACK节点。-->注意：RED树不可能出现两个红色节点连续的情况，但是会出现两个黑节点的情况
* 5.从任意节点到叶子节点都有相同数目的黑节点（BLACK）
* 注意：在判定是否是红黑树的时候一定要注意不要忘了虚拟的黑节点。
* ----------------------------------------------------------------------------------------
*红黑树与四阶B树（2-4树）的等价性
* 红黑树的黑节点与它的红色子节点结合成一个B树子节点
* 红黑树黑节点的数目就是对应b树节点的数目
* -------------------------------------------------
* 涉及到的概念
* parent父节点
* sibling 兄弟节点
* uncle叔父节点
* grand祖父节点
* @param <E>
*/
public class RBTree<E> extends BBST<E> {
public static final boolean RED=false;
public static final boolean BLACK=true;
public RBTree() {
this(null);
}
public RBTree(Comparator<E> comparator) {
super(comparator);
}
/**
* 添加：如果第一次添加的是根节点，但是默认颜色为红色，所以需要将其染黑
*
* |-----红---黑---红
* | | | |
* 红---黑---红 黑--红 红--黑 黑
* 4 3 3 2
* 1.有四种情况直接满足红黑树的性质，父节点parent为黑节点--->不可能造成两个红节点连续的情况
* 2.其余八种父节点（parent）需要特殊处理---又按照叔父节点是红色和叔父节点是黑色划分，叔父节点是红色的会发生上溢
* 。但是叔父节点为黑色另有不同--->LL RR LR RL （grand进行单旋）
* @param node 新添加的节点->太秒了
*/
@Override
protected void afterAdd(Node<E> node) {
Node<E> parent=node.parent;
//这个代码块包括两种情况--->（1）第一次添加节点（2）叔父节点是红色的情况下，上溢到了根节点
if(parent==null){
black(node);
root=node;
return;
}
if(isBlack(parent))
{
//排除本身就满足条件的哪四种情况,不需要额外处理
return;
}
Node<E> uncle=parent.sibling();
Node<E> grand=parent.parent;
//叔父节点是红色-->发生上溢
if(isRed(uncle)){
//上溢分裂的情况
black(parent);
black(uncle);
//把祖父节点当成一个新添加的节点加到上面-->解决上溢
afterAdd(red(grand));
return;
}
//叔父节点不是红节点
if(parent.isLeftChild())
{
//由于染色顺序并不影响所以可以把统一的染色顺序放在前面red(grand)
//LL RR 单旋
if(node.isLeftChild()){//LL
black(parent);
red(grand);
}else {//LR
black(node);
red(grand);
rotateLeft(parent);
}
rotateRight(grand);
}else{
if(node.isRightChild())//RR
{
black(parent);
red(grand);
}else{//RL
black(node);
red(grand);
rotateRight(parent);
}
rotateLeft(grand);
}
}
/**
* b树中最后被删除的一定都在叶子节点中
* 删除红色节点--->不会影响红黑树的性质就直接进行删除就行
*
*
*/
//删除黑色节点要传入黑色节点的替代节点
@Override
protected void afterRemove(Node<E> node, Node<E> replacement) {
//b树类比红黑树一定是删除的最后一层。如果要删除的是红色，由于黑色是主体，
// 所以要删除的节点一定度为0的红色叶子节点，不会影响原本红黑树的规则，所以不用调整，直接结束函数
if(isRed(node)){
return;
}
/**
* 一定要清楚afterRemove的作用是删除之后的调整，不是主体删除方法。
* 作用：对于不符合红黑树性质的操作及时进行调整
*
* 问：对于删除度为2的黑色节点，是不是可是囊括
* 答：可以：因为删除度为2的黑色节点，找到前驱后，还是删除红色节点不用处理，染黑替代节点并不影响，因为已经删除
*
* 为什么黑色节点的替代不能为黑色节点
* 因为b树的删除都是在最后一层进行操作，如果黑色节点子节点依然是一个黑色节点，由于黑色才是主体
* 不会融入到一个节点中，所以只会向下增高一层，不符合删除在最后一层操作。，
*/
if(isRed(replacement)){
//染黑：避免出现连续两个红色节点
black(replacement);
return;
}
/**
* 处理最后一种情况-->删除度为0的黑色叶子节点的调整方法
*
* 删除度为0的黑色叶子节点的调整方法肯定会造成下溢
* 补救:(1)看看兄弟节点能不能借
* a:兄弟节点能借的条件：1.兄弟节点是黑色 2.兄弟节点至少拥有一个红色子节点
* ----------------------------------------
* 能借后做出的操作：
* ?进行旋转操作
* ?旋转之后的中心节点继承 parent 的颜色
* ?旋转之后的左右节点染为 BLACK（因为此时红色子节点已经旋上去了）
*
* 旋转有三种情况：LL LR LL
*
* 🤩🤩特殊情况1：
* 如果被删除的是黑色，它的父节点也是黑色，删除后黑色父节点也会向下合并，造成父节点继续下溢
*只需将这个父节点当成一个新的被删除的黑色节点递归调用afterRemove方法，重复利用代码
*
* 🤩🤩特殊情况2：
* 🚩🚩🚩如果兄弟节点是红色，对于b树的性质，【黑色节点与其红色节点组成一个b树节点】
* 可知：红色节点一定在父节点中-->红色的节点的子节点一定是黑的，可以借侄子的【想办法将侄子变成兄弟】
* 强制将侄子变成兄弟再次套用兄弟节点是黑色是的代码
*-----------------------------------------------
*/
Node<E> parent=node.parent;
if(parent==null)
{
return;
}
//这么写有问题：node已经被删除--->指向node的线已经断了
//Node<E> sibling =node.sibling();
/**
* 需要间接求出兄弟节点
* 只需知道被删除的节点先前是在parent的左边还是右边，进而知道sibling是parent.left还是parent.right
*/
/**
* 为什么以此作为判定标准：
* 因为在二叉搜索树的删除中，删除黑色叶子节点,已经将一边置为null
* if (node == node.parent.left) {
* node.parent.left=null;
* } else { // node == node.parent.right
* node.parent.right=null;
* }
*/
//有特殊情况
boolean left=parent.left==null||node.isLeftChild();
Node<E> sibling=left?parent.right:parent.left;
if(left){//node是在左子树，兄弟节点在右边
if(isRed(sibling)){
black(parent);
red(sibling);
rotateLeft(parent);
//更新兄弟
sibling=parent.right;
}
//兄弟节点是黑色-->判断是否有红色子节点
//没有一个红色子节点--->父节点向下合并
/**
* 为什么以父节点是不是黑的为判定条件
* 因为如果父节点是红色，那它肯定不是主体，向下合并后，parent本身并没有下溢
* 如果父节点是黑色，那他向下合并后，自身也会下溢
*
*/
if(isBlack(sibling.left)&&isBlack(sibling.right)){
boolean parentBlack=isBlack(parent);
black(parent);
red(sibling);
//这种情况父节点向下合并，父节点的位置也会下溢
if(parentBlack){
//三黑局面没有替代节点
afterRemove(parent,null);
}
}else {//至少有一个红色子节点
//判断是LL LR.....
//三种情况:LL LR (LL或LR)
//可以先统一进行左旋转然后在统一进行右旋转
//如何区分LR左子节点是黑的
if(isBlack(sibling.left)) {//LR情况
rotateLeft(sibling);
//左旋转后兄弟节点已经发生了变化
sibling = parent.left;
}
//LL 情况
//现在的sibling已经更新过是图中的78
color(sibling,iscolor(parent));
black(parent);
black(sibling.left);
rotateRight(parent);
}
}else {//node是在右子树，兄弟节点在左边
//🤩🤩特殊情况2：
if(isRed(sibling)){
black(parent);
red(sibling);
rotateRight(parent);
//更新兄弟
sibling=parent.left;
}
//兄弟节点是黑色-->判断是否有红色子节点
//没有一个红色子节点--->父节点向下合并
/**
* 为什么以父节点是不是黑的为判定条件
* 因为如果父节点是红色，那它肯定不是主体，向下合并后，parent本身并没有下溢
* 如果父节点是黑色，那他向下合并后，自身也会下溢
*
*/
if(isBlack(sibling.left)&&isBlack(sibling.right)){
boolean parentBlack=isBlack(parent);
black(parent);
red(sibling);
//这种情况父节点向下合并，父节点的位置也会下溢
if(parentBlack){
//三黑局面没有替代节点
afterRemove(parent,null);
}
}else {//至少有一个红色子节点
//判断是LL LR.....
//三种情况:LL LR (LL或LR)
//可以先统一进行左旋转然后在统一进行右旋转
//如何区分LR左子节点是黑的
if(isBlack(sibling.left)) {//LR情况
rotateLeft(sibling);
//左旋转后兄弟节点已经发生了变化
sibling = parent.left;
}
//LL 情况
//现在的sibling已经更新过是图中的78
color(sibling,iscolor(parent));
black(parent);
black(sibling.left);
rotateRight(parent);
}
}
}
@Override
protected Node<E> createNode(E element, Node<E> parent) {
return new RBNode<>(element,parent);
}
//染色--->好处parent=color(node.parent,color)--->染色的同时还能更新node的parent
private Node<E> color(Node<E> node,boolean color){
//代码习惯：染色的同时返回被染色的节点便于对其进行一些操作
if(node==null)
{
return null;
}
((RBNode<E>)node).color=color;
return node;
}
public Node<E> red(Node<E> node)
{
return color(node,RED);
}
public Node<E> black(Node<E> node)
{
return color(node,BLACK);
}
//判断颜色
private boolean iscolor(Node<E> node)
{
return node==null?BLACK:((RBNode<E>)node).color;
}
public boolean isRed(Node<E> node)
{
return iscolor(node)==RED;
}
public boolean isBlack(Node<E> node){
return iscolor(node)==BLACK;
}
//自定义内部类-->红黑树类型
public static class RBNode<E>extends Node<E>{
boolean color=RED;
//为什么默认为红色：因为默认为红色的情况下对于红黑树的五个条件除了第四个条件都满足，更加的适合进行默认颜色
//更容易使红黑树的性质得到满足
//4不满足的可能情况使出现两个连续的红色子节点
public RBNode(E element, Node<E> parent) {
super(element, parent);
}
//内部类重新定义一个方法--->返回兄弟节点
//不用定义返回叔父节点-->因为node.parent.sibling()-->就是叔父节点
public Node<E> sibling()
{
if(isLeftChild())
{
return parent.right;
}
if(isRightChild()){
return parent.left;
}
return null;
}
@Override
public String toString() {
String str="";
if(color==RED){
str="R_";
}
return str+element.toString();
}
}
}
