动态规划
示例 最长回文子串
给你一个字符串 s,找到 s 中最长的回文子串。(回文串:一串正着读和反着读都是一样的一种特殊字符串 )
输入:s = "babad"
输出:"bab"
解释:"aba" 同样是符合题意的答案。
暴力解法
思路:
根据回文串的概念,进行解题
public class Solution{
public static void main(String[] args) {
String str = "babad";
String solution = lengthOfLIS(str);
System.out.println("&&&&&"+solution);
}
public static String lengthOfLIS(String str) {
// 校验参数
int length = str.length();
if (length < 2) {
return str;
}
//定义两个int 用来记录下标
int maxlen = 1;
int begin =0;
//str.charAt(0);每一次都会检查是否越界 所以我们要先把字符串转换为数组减少开销
char[] charArray = str.toCharArray();
//主要逻辑,主要获取子回文串
for (int i = 0; i < length-1; i++) {
for (int j = i+1; j < length; j++) {
if(j-i +1 >maxlen && voildPalind(charArray,i,j)){
maxlen = j - i + 1 ;
begin = i;
}
}
}
return str.substring(begin,begin+maxlen
);
}
//校验是否是回文串
private static boolean voildPalind(char[] charArray, int left, int right) {
while (left < right){
if (charArray[left]!=charArray[right]) {
return false;
}
left++;
right--;
}
return true;
}
}
时间复杂度 :有两个for循环 还有一次遍历

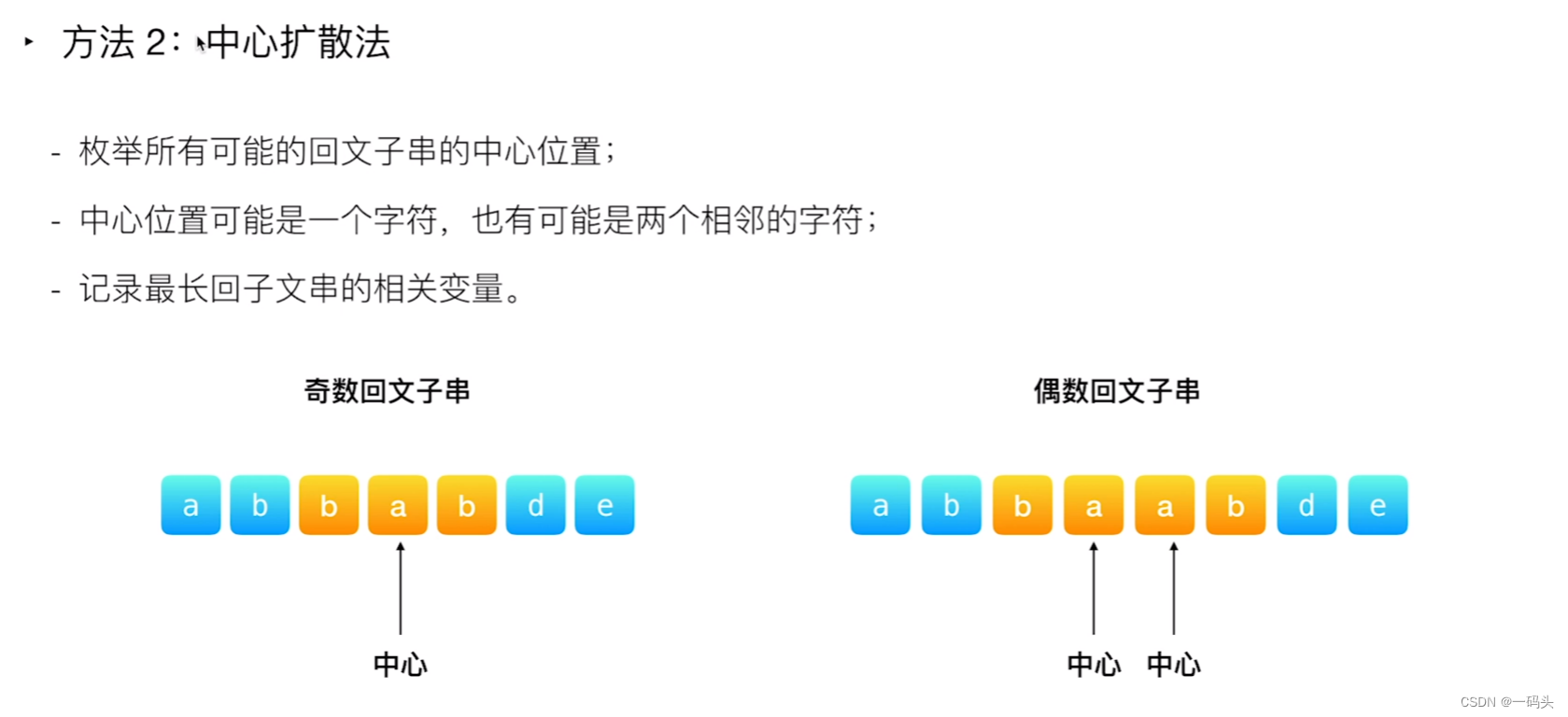
中心扩展算法
中心扩散法怎么去找回文串?
从每一个位置出发,向两边扩散即可。遇到不是回文的时候结束。举个例子,str = acdbbdaastr=acdbbdaa 我们需要寻找从第一个 b(位置为 33)出发最长回文串为多少。怎么寻找?
首先往左寻找与当期位置相同的字符,直到遇到不相等为止。
然后往右寻找与当期位置相同的字符,直到遇到不相等为止。
最后左右双向扩散,直到左和右不相等。
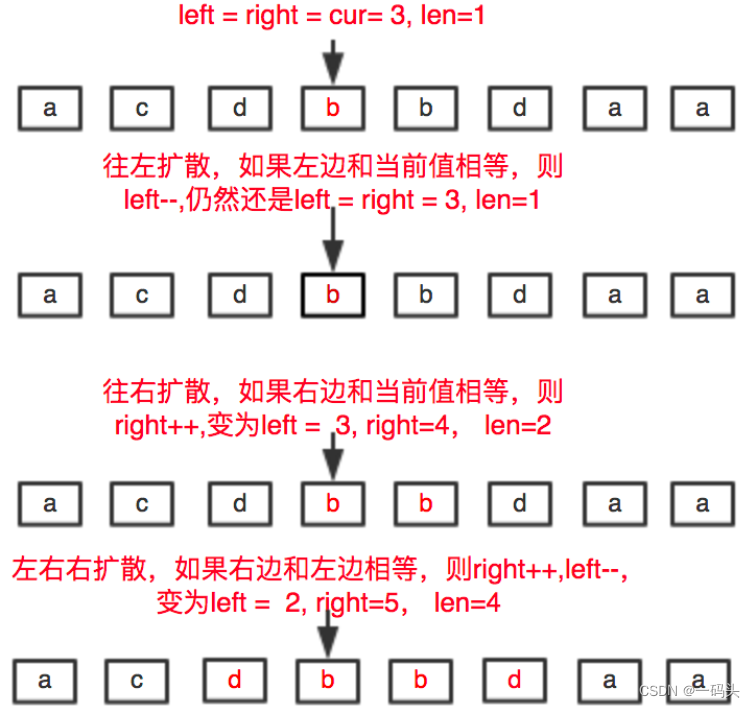
每个位置向两边扩散都会出现一个窗口大小(len)。如果 len>maxLen(用来表示最长回文串的长度)。则更新 maxLen 的值。
因为我们最后要返回的是具体子串,而不是长度,因此,还需要记录一下 maxLen 时的起始位置(maxStart),即此时还要 maxStart=len。
public String longestPalindrome1(String s) {
if (s == null || s.length() == 0) {
return "";
}
int strLen = s.length();
int left = 0;
int right = 0;
int len = 1;
int maxStart = 0;
int maxLen = 0;
for (int i = 0; i < strLen; i++) {
left = i - 1;
right = i + 1;
while (left >= 0 && s.charAt(left) == s.charAt(i)) {
len++;
left--;
}
while (right < strLen && s.charAt(right) == s.charAt(i)) {
len++;
right++;
}
while (left >= 0 && right < strLen && s.charAt(right) == s.charAt(left)) {
len = len + 2;
left--;
right++;
}
if (len > maxLen) {
maxLen = len;
maxStart = left;
}
len = 1;
}
return s.substring(maxStart + 1, maxStart + maxLen + 1);
}
public static void main(String[] args) {
String str = "babad";
String solution = longestPalindrome(str);
System.out.println("&&&&&"+solution);
}
private static String longestPalindrome(String str) {
//校验参数
int length = str.length();
if (str == null || str.length() < 1) {
return "";
}
//定义开始结束下标
int start = 0, end = 0;
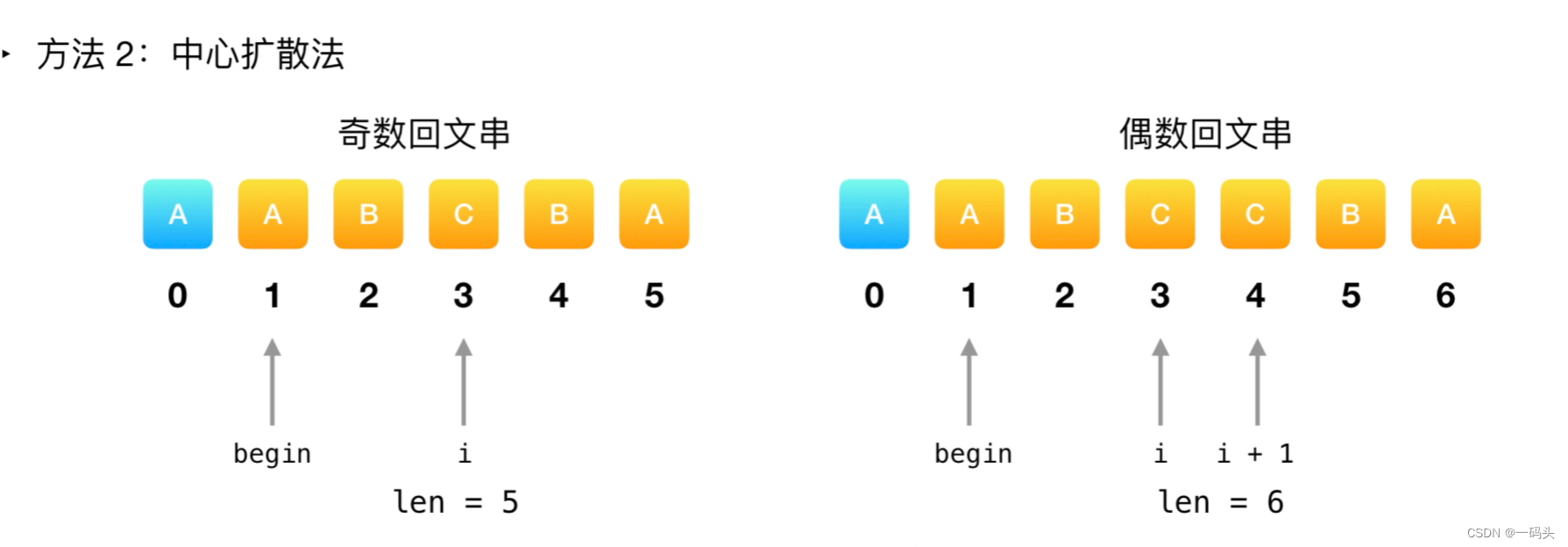
for (int i = 0; i <length ; i++) {
//中心为单数的情况
int len1 = expandAroundCenter(str, i, i);
//中心为偶数的情况
int len2 = expandAroundCenter(str, i, i + 1);
int len = Math.max(len1, len2);
if (len > end - start) {
//边界值 通过观察图二而得到
start = i - (len - 1) / 2;
end = i + len / 2;
}
}
return str.substring(start, end + 1);
}
public static int expandAroundCenter(String s, int left, int right) {
//定义边界值
while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
//向两边扩散
--left;
++right;
}
//返回最大回文串长度
return right - left - 1;
}
时间复杂度:

动态规划解法
思路:回文串天然具有状态转移的属性,因为讲回文串的两端去掉之后,剩下的部分依然是回文串,所以得出结论,这个字符串是否是回文串,是由中间部分是否是回文决定的
是回文串

不是回文串

所以得出状态转移方程

动态规划实际上是填写一张二维表格
举例子:

实现:
public class Solution {
public String longestPalindrome(String s) {
int len = s.length();
if (len < 2) {
return s;
}
int maxLen = 1;
int begin = 0;
// dp[i][j] 表示 s[i..j] 是否是回文串 java中boolean类型二维数组默认是false
boolean[][] dp = new boolean[len][len];
// 初始化:所有长度为 1 的子串都是回文串 对角线上的元素都为true
for (int i = 0; i < len; i++) {
dp[i][i] = true;
}
char[] charArray = s.toCharArray();
// 递推开始
// 先枚举子串长度
for (int L = 2; L <= len; L++) {
// 枚举左边界,左边界的上限设置可以宽松一些
for (int i = 0; i < len; i++) {
// 由 L 和 i 可以确定右边界,即 j - i + 1 = L 得
int j = L + i - 1;
// 如果右边界越界,就可以退出当前循环
if (j >= len) {
break;
}
if (charArray[i] != charArray[j]) {
dp[i][j] = false;
} else {
if (j - i < 3) {
dp[i][j] = true;
} else {
dp[i][j] = dp[i + 1][j - 1];
}
}
// 只要 dp[i][L] == true 成立,就表示子串 s[i..L] 是回文,此时记录回文长度和起始位置
if (dp[i][j] && j - i + 1 > maxLen) {
maxLen = j - i + 1;
begin = i;
}
}
}
return s.substring(begin, begin + maxLen);
}
}
Manacher 算法
太难了,有时间研究研究
链接:https://leetcode.cn/problems/longest-palindromic-substring/solution/zhong-xin-kuo-san-fa-he-dong-tai-gui-hua-by-reedfa/
来源:力扣(LeetCode)