[数据结构与算法] 【数据结构】手撕排序算法（下）完美散花快速排序的非递归、归并排序的非递归（校招、面试必掌握）、基数排序（桶排序）、计数排序、七大排序的性能测试以及总结

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 【数据结构】手撕排序算法（下）完美散花快速排序的非递归、归并排序的非递归（校招、面试必掌握）、基数排序（桶排序）、计数排序、七大排序的性能测试以及总结 -> 正文阅读

[数据结构与算法]【数据结构】手撕排序算法（下）完美散花快速排序的非递归、归并排序的非递归（校招、面试必掌握）、基数排序（桶排序）、计数排序、七大排序的性能测试以及总结

文章目录

1. 前言

在上面两篇文章中，我们分别学习了插入排序（直接插入排序、希尔排序）、选择排序（直接选择排序、堆排序）、交换排序（冒泡排序、快速排序的递归写法）、归并排序的递归写法。那么，在这一节中，我们将学习快速排序的非递归写法、归并排序的非递归写法。以及，我们还要掌握最后两种不是很常见的排序，一个是基数排序（桶排序），一个是计数排序。最后我们要对我们所学的七大排序的性能进行测试和总结。

2. 递归的劣势（坏处）

如果我们递归的深度太深，程序是没有错误的，但是栈的空间会不够用，会发生栈溢出。操作系统中，栈的空间大小大概是 8M~10M左右吧。

在这里插入图片描述
递归改为非递归大概有两种方法：

直接该循环（简单）
借助数据结构的栈模拟递归过程（相对会比较复杂）

3. 快速排序（非递归）

快速排序的递归改为非递归形式我们是采用数据结构中的栈模拟递归过程，会比较复杂一点。如果我们没有学过C++的STL的话，需要自己写一个栈，会比较麻烦。这里我们采用C++自身就提供的栈容器stack。对于用数据结构中的栈模拟递归的过程：我们是将数组的左右下标入栈，然后取出下标，完成操作。由于栈是先进后出的，为了更加真是的模拟递归，我们先将数组的由下标入栈，然后再入左下标，这样先拿出来的就是左下标。（当然也可以不是这样顺序，只要能取出来就行了）

//快排  非递归
//利用数据结构的栈模拟递归过程
void QuickSortNonR(int* a, int n)
{
	stack<int> st;//利用栈容器创建一个整形类型的栈
	st.push(n - 1);//入栈 入的是数组的右下标
	st.push(0);//入栈 入的是数组的左下标
	while (!st.empty())//当栈不为空 栈里还有元素 说明还需要排
	{
		int left = st.top();//左下标 获取栈顶元素
		st.pop();//出栈

		int right = st.top();//右下标 获取栈顶元素
		st.pop();//出栈

		int keyIndex = PartSort1(a, left, right);//挖坑法 
		//[left,keyIndex-1] keyIndex [keyIndex+1,right]
		if (keyIndex + 1 < right)//同样 入栈的时候，我们先把有区间入栈，那么拿出来的先是左区间
		{
			st.push(right);//入栈 右区间 右下标 数组最后一个元素
			st.push(keyIndex + 1);//入栈 右区间 左下标 数组第一个一个元素
		}
		if (left < keyIndex - 1)
		{
			st.push(keyIndex - 1);//入栈 左区间 右下标 数组最后一个元素
			st.push(left);//入栈 左区间 左下标 数组第一个一个元素
		}
	}
}

4. 归并排序（非递归）

归并排序，也称为外排序。对于归并排序非递归的实现，我们使用直接循环就可以解决了。因为归并排序本来就是先分解成一个一个元素的，那么当gap = 1 时（gap为每组的数据个数），我们就直接让两两元素进行归并。但是在归并排序的非递归的过程中，会有很多的坑，因为我们排序的数组并不是每次都能分成两两一组的。注意①归并过程中右半区间可能不存在；注意②归并过程中右半区间算多了，需要修正一下

在这里插入图片描述

//归并排序 非递归
void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);//开辟的临时数组
	int gap = 1;//每组的数据个数
	while (gap < n)
	{
		for (int i = 0; i < n; i += 2 * gap)
		{
			//[i,i+gap-1] [i+gap,i+2*gap-1]
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;
			//1.归并过程中右半区间可能不存在
			if (begin2 >= n)
			{
				break;
			}
			//2.归并过程中右半区间算多了，需要修正一下
			if (end2 >= n)
			{
				end2 = n - 1;
			}
			//归并过程
			int index = i;
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] <= a[begin2])
				{
					tmp[index++] = a[begin1++];//后置++
				}
				else
				{
					tmp[index++] = a[begin2++];//后置++
				}
			}
			while (begin1 <= end1)
			{
				tmp[index++] = a[begin1++];//后置++
			}
			while (begin2 <= end2)
			{
				tmp[index++] = a[begin2++];//后置++
			}
			//拷贝回去
			for (int j = 0; j <= end2; ++j)
			{
				a[j] = tmp[j];
			}
		}
		gap *= 2;
	}
}

5. 七大排序的性能测试

我们对10万个数进行排序，大家记得打开release版本哦，不然debug太慢了。可以多测试几遍。

//测试排序的性能对比
void TestOP()
{
	srand(time(0));
	const int N = 100000;
	int* a1 = (int*)malloc(sizeof(int) * N);
	int* a2 = (int*)malloc(sizeof(int) * N);
	int* a3 = (int*)malloc(sizeof(int) * N);
	int* a4 = (int*)malloc(sizeof(int) * N);
	int* a5 = (int*)malloc(sizeof(int) * N);
	int* a6 = (int*)malloc(sizeof(int) * N);
	int* a7 = (int*)malloc(sizeof(int) * N);

	//给数组赋随机值
	for (int i = 0; i < N; ++i)
	{
		a1[i] = rand();
		a2[i] = a1[i];
		a3[i] = a1[i];
		a4[i] = a1[i];
		a5[i] = a1[i];
		a6[i] = a1[i];
		a7[i] = a1[i];
	}

	int begin1 = clock();//clock函数是表示函数在这个时间点运行的时间是多少
	InsertSort(a1, N);
	int end1 = clock();

	int begin2 = clock();
	ShellSort(a2, N);
	int end2 = clock();

	int begin3 = clock();
	SelectSort(a3, N);
	int end3 = clock();

	int begin4 = clock();
	HeapSort(a4, N);
	int end4 = clock();

	int begin5 = clock();
	BubbleSort(a5, N);
	int end5 = clock();

	int begin6 = clock();
	QuickSort(a6, 0, N - 1);
	int end6 = clock();

	int begin7 = clock();
	MergeSort(a7, N);
	int end7 = clock();

	printf("InsertSort:%d\n", end1 - begin1);
	printf("ShellSort:%d\n", end2 - begin2);
	printf("SelectSort:%d\n", end3 - begin3);
	printf("HeapSort:%d\n", end4 - begin4);
	printf("BubbleSort:%d\n", end5 - begin5);
	printf("QuickSort:%d\n", end6 - begin6);
	printf("MergeSort:%d\n", end6 - begin6);

	free(a1);
	free(a2);
	free(a3);
	free(a4);
	free(a5);
	free(a6);
	free(a7);
}

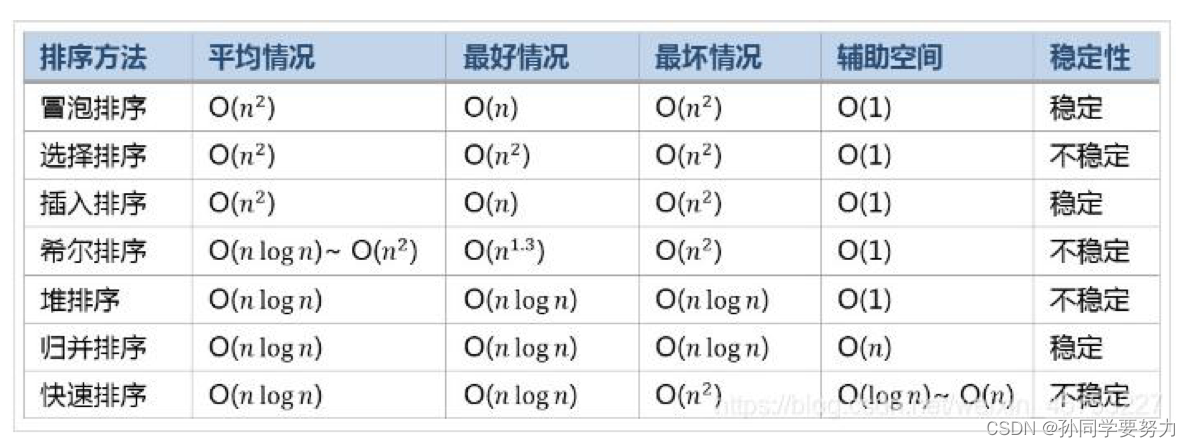
在这里插入图片描述

6. 七大排序的总结

在这里插入图片描述

7. 计数排序

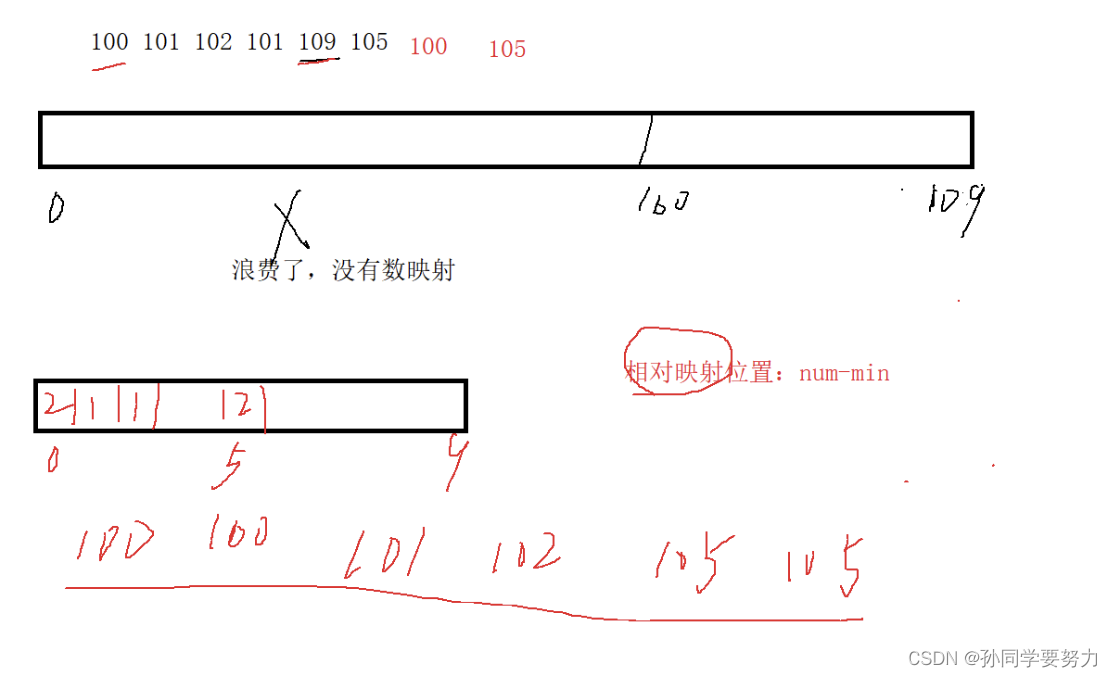
计数排序就是统计每个数出现的次数。我们需要开辟一个数组，数组的长度由这组序列中最大的那个数来决定。

计数排序总结：

计数排序是一种非比较排序
计数排序的思想很巧，适用于范围比较集中的一组整形数据排序
时间复杂度：O（N + range）
空间复杂度：O（range）

在这里插入图片描述

但是，如果数组中的数字相差很大的话，那么我们会浪费很多的空间。我们可以采取一种方法：用最大的数减去最小的那个数。但是，最后我们采取下标的话，要 ± 那个相隔的大小。

在这里插入图片描述

//计数排序
void CountSort(int* a, int n)
{
	int max = a[0], min = a[0];
	//先找出最大值和最小值
	for (int i = 0; i < n; ++i)
	{
		if (a[i] > max)
		{
			max = a[i];
		}
		if (a[i] < min)
		{
			min = a[i];
		}
	}
	int range = max - min + 1;//相对映射范围
	int* count = (int*)malloc(sizeof(int) * range);
	memset(count, 0, sizeof(int) * range);//把a[i]都赋值为0
	//统计次数
	for (int i = 0; i < n; ++i)
	{
		count[a[i] - min]++;
	}
	int j = 0;
	for (int i = 0; i < range; ++i)
	{
		while (count[i]--)//后置--
		{
			a[j++] = i + min;//后置++
		}
	}
	free(count);
}