1. 排序算法

在这里插入图片描述
排序算法的详细教程见官方文档
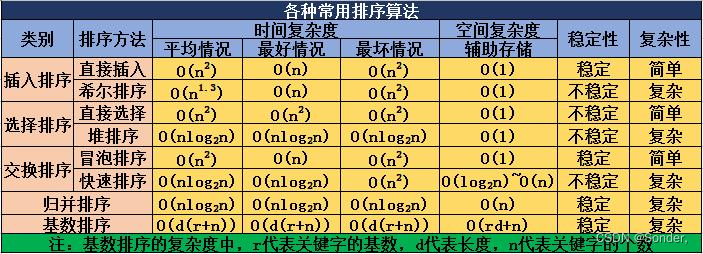
下面是几种常见的排序算法

1.1 插入排序

将第一待排序序列第一个元素看做一个有序序列，把第二个元素到最后一个元素当成是未排序序列。
从头到尾依次扫描未排序序列，将扫描到的每个元素插入有序序列的适当位置。（如果待插入的元素与有序序列中的某个元素相等，则将待插入元素插入到相等元素的后面。）

function insertionSort(arr) {
    const n = arr.length
    for (let i = 1; i < n; i++) {
        let pre = i - 1
        let cur = arr[i]
        while (arr[pre] > cur && pre >= 0) { //当前面的元素大于该轮的i，则应该将前面的元素后移一位，直到找到i的插入位置
            arr[pre + 1] = arr[pre]
            pre--
        }
        arr[pre + 1] = cur //由于上面循环有一个pre--，所以这里i的位置需要pre+1
    }
    return arr
}

1.2 直接选择

首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置。
再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。
重复第二步，直到所有元素均排序完毕。

function selectionSort(arr) {
    const n = arr.length
    let temp
    for (let i = 0; i < n; i++) {
        temp = i
        for (let j = i + 1; j < n; j++) {
            temp = arr[j] < arr[temp] ? j : temp //保存最小值的下标
        }
        [arr[i], arr[temp]] = [arr[temp], arr[i]] //将最小值和i的值互换

    }
    return arr
}

1.3 冒泡排序

太简单了，直接看

function bubbleSort(arr) {
    const n = arr.length
    for (let i = 0; i < n; i++) {
        for (let j = 0; j < n - i - 1; j++) {
            arr[j] > arr[j + 1] ? [arr[j + 1], arr[j]] = [arr[j], arr[j + 1]] : [] // 相邻元素两两对比，升序
        }
    }
    return arr
}

1.4 快速排序

从数列中挑出一个元素，称为 “基准”（pivot）;
重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序

function quickSort(arr) {
    if (arr.length <= 1) return arr
    let middleIndex = Math.floor(arr.length / 2);
    let middle = arr.splice(middleIndex, 1);
    let left = [];
    let right = [];
    for (let i = 0; i < arr.length; i++) {
        if (arr[i] < middle) {
            left.push(arr[i])
        } else {
            right.push(arr[i])
        }
    }
    return quickSort(left).concat(middle, quickSort(right))
}

2. sort实现原理

V8的sort函数包含两种排序 InsertionSort 和 QuickSort，数量小于10 的数组使用 InsertionSort，大于10 的数组使用 QuickSort

2.1 使用

当没有参数传入的时候，其排序顺序默认为，将待排序数据转换为字符串，并按照Unicode序列排序
可自定义函数按需进行排序

let arr = [2, 3, 1, 33, 11, 22, '23', '111', 567]
console.log(arr.sort())
console.log(arr.sort(function(a, b) {
    return a - b
}))

在这里插入图片描述

2.2 原理

当数组长度小于等于10的时候，采用插入排序，大于10的时候，采用快排。
V8源码
插入排序

function InsertionSort(a, from, to) {
    for (var i = from + 1; i < to; i++) {
      var element = a[i];
      for (var j = i - 1; j >= from; j--) {
        var tmp = a[j];
        var order = comparefn(tmp, element);
        if (order > 0) {
          a[j + 1] = tmp;
        } else {
          break;
        }
      }
      a[j + 1] = element;
    }
  };

快速排序

function GetThirdIndex(a, from, to) {//获取关键值
    var t_array = new InternalArray();
    // Use both 'from' and 'to' to determine the pivot candidates.
    var increment = 200 + ((to - from) & 15);
    var j = 0;
    from += 1;
    to -= 1;
    for (var i = from; i < to; i += increment) {
      t_array[j] = [i, a[i]];
      j++;
    }
    t_array.sort(function(a, b) {
      return comparefn(a[1], b[1]);
    });
    var third_index = t_array[t_array.length >> 1][0];
    return third_index;
  }

  function QuickSort(a, from, to) {
    var third_index = 0;
    while (true) {
      // Insertion sort is faster for short arrays.
      if (to - from <= 10) {//数组长度小于等于10的时候，插入排序
        InsertionSort(a, from, to);
        return;
      }
      if (to - from > 1000) {//数组长度大于1000的时候，获取关键值
        third_index = GetThirdIndex(a, from, to);
      } else {//长度大于10小于等于1000的时候，取数组中间的元素作为关键值
        third_index = from + ((to - from) >> 1);
      }
      // Find a pivot as the median of first, last and middle element.
      var v0 = a[from];
      var v1 = a[to - 1];
      var v2 = a[third_index];
      var c01 = comparefn(v0, v1);
      if (c01 > 0) {
        // v1 < v0, so swap them.
        var tmp = v0;
        v0 = v1;
        v1 = tmp;
      } // v0 <= v1.
      var c02 = comparefn(v0, v2);
      if (c02 >= 0) {
        // v2 <= v0 <= v1.
        var tmp = v0;
        v0 = v2;
        v2 = v1;
        v1 = tmp;
      } else {
        // v0 <= v1 && v0 < v2
        var c12 = comparefn(v1, v2);
        if (c12 > 0) {
          // v0 <= v2 < v1
          var tmp = v1;
          v1 = v2;
          v2 = tmp;
        }
      }
      // v0 <= v1 <= v2
      a[from] = v0;
      a[to - 1] = v2;
      var pivot = v1;
      var low_end = from + 1;   // Upper bound of elements lower than pivot.
      var high_start = to - 1;  // Lower bound of elements greater than pivot.
      a[third_index] = a[low_end];
      a[low_end] = pivot;

      // From low_end to i are elements equal to pivot.
      // From i to high_start are elements that haven't been compared yet.
      partition: for (var i = low_end + 1; i < high_start; i++) {
        var element = a[i];
        var order = comparefn(element, pivot);
        if (order < 0) {
          a[i] = a[low_end];
          a[low_end] = element;
          low_end++;
        } else if (order > 0) {
          do {
            high_start--;
            if (high_start == i) break partition;
            var top_elem = a[high_start];
            order = comparefn(top_elem, pivot);
          } while (order > 0);
          a[i] = a[high_start];
          a[high_start] = element;
          if (order < 0) {
            element = a[i];
            a[i] = a[low_end];
            a[low_end] = element;
            low_end++;
          }
        }
      }
      if (to - high_start < low_end - from) {
        QuickSort(a, high_start, to);
        to = low_end;
      } else {
        QuickSort(a, from, low_end);
        from = high_start;
      }
    }
  };

v8的sort对于长度大于1000的数组，采用的是快排与插入排序混合的方式进行排序的，因为，当数据量很小的时候，插入排序效率优于快排。

快排需要选择一个关键值，并且以关键值作为基准开始排序，比关键值的值大的放在关键值右边，小的放在关键值左边，由此完成一趟排序；然后再对关键值左侧的数据以及右侧的数据分别执行快排。如果每次关键字选择都是一组数据的最小值或者最大值，那么快排的复杂度将会达到n^2，就跟冒泡没什么区别了。在快排算法中，最优的关键值，是这组数据最中间位置的值，这样才能可以使得排序算法复杂度达到nlogn. 因此，关键值的选择尤为重要。

v8快排关键值的获取：

获取临时关键值tmp：

对于大于10小于等于1000的数据量，tmp为这组数据中间位置的值
对于大于1000的数据，根据一定步长从待排序的数组里面获取一组临时数据，对临时数据排序，再获得临时数据中最中间位置的值，作为待排序数组的tmp。步长的计算跟数组的长度有关系，其计算方法如下：
步长 = 200 + 数组长度&15;
将数组的长度转换为二进制后，与1111按位与，其结果与200相加，作为步长。

计算关键值key：

获取数组第一个数a0, 最后一个数an；
比较a0, tmp, an, 赋值给v0, v1, v2, 保证v0<=v1<=v2;
关键值 = v1.

3. 快排的优化

快排存在的问题：
当partition操作时,如果每次取得的的第一个元素趋近于最值,使得分治的任务极度不平衡,情况最坏时,快速排序算法的复杂度将上升到O(n2)
存在大量重复键值时,同样会出现分治任务很不平衡的情况

排序算法名称	针对的应用情景
快速排序	无序数组(对于基本有序数组和大量重复键值的数组复杂度上升至O(n2)
随机速排	快速排序的优化,解决普通快排在部分有序数组中进行排序,每次取得的都是趋近最值
二路快排	随机速排的优化,解决数组中存在大量键值重复的情况以及基本有序数组
三路快排	二路排序的优化，把等于value的元素放在另一个区间内，不参与下次的排序。

3.1 随机快排

在每次partition的过程中,将left到right-1之间的随机选取一个元素,与right进行位置交换,这样就解决了快排中如果数组部分有序,数组划分不平衡的情况
缺点：当数组中存在大量重复键值的时候任然会出现算法复杂度上升的情况

int ranNum = left + (int)(Math.random()*(right-left+1));
        //把随机数作为索引,将索引对应值与最后一位值 right 交换

3.2二路快排

在双路快排中，有两个游标，分别在数组的start位置（游标A）和end位置（游标B），游标A从start开始向右寻找大于base（仍然取第一项）的值，游标B从end开始想做寻找小于等于base的值，然后将两个值进行位置互换，然后接着寻找，直到两个游标相遇，将相遇位置的值和base值进行位置互换。这样一次寻找过程结束，接下来对于左右两段进行重复的操作，直至整个数组排序完成。

function quickSort(arr, start = 0, end = arr.length - 1) {
    // 终止条件
    if (start >= end) return false;
    let left = start, right = end, base = arr[start];
    while (left < right) {
        // 从右向左，寻找第一个小于base的值
        while (arr[right] > base && right >= left) right --;
        // 从左向右，寻找第一个大于base的值
        while (arr[left] <= base && left < right) left ++;
        // 将两个值交换位置
        [arr[left], arr[right]] = [arr[right], arr[left]];
    }
    // 将最后两个游标相遇的位置的值与base值交换
    [arr[start], arr[left]] = [arr[left], arr[start]];
    fastSort(arr, start, left - 1);
    fastSort(arr, right + 1, end)
}

3.3三路快排

三路快速排序是快速排序的的一个优化版本，将数组分为三段，即小于基准元素、等于基准元素和大于基准元素，这样能够比较高效的处理数组中存在相同元素的状况,其它特征与快速排序基本相同。

function qSort3(arr) {       //三路快排
	if(arr.length == 0) {
		return [];
	}
	var left = [];
	var center = [];
	var right = [];
	var pivot = arr[0];    //偷懒，直接取第一个,实际取值状况 参考[快速排序算法的优化思路总结]
	for(var i = 0; i < arr.length; i++) {      
		if(arr[i] < pivot) {
			left.push(arr[i]);
		} else if(arr[i] == pivot) {
			center.push(arr[i]);
		} else {
			right.push(arr[i]);
		}
	}
	return [...qSort3(left), ...center, ...qSort3(right)];
}