[数据结构与算法]python数据结构与算法学习之顺序与查找

顺序查找

• 在Python List中，数据项的存储位置称为下标（index），这些下标都是有序的整数。通过下标，我们就可以按照顺序来访问和查找数据项，这种技术称为“顺序查找”。
• 顺序查找是从列表中的第一个数据项开始。按照下标增长的顺序，逐个比对数据项，如果到最后一个都未发现要查找的项，那么查找失败。

1. 顺序查找：无序表查找代码
算法复杂度是O(n)

def sequentialSearch(alist, item):
    pos = 0
    found = False
    
    while pos < len(alist) and not found:
        if alist[pos] == item:
            found = True
        else:
            pos = pos + 1   # 下标顺序增长
   
    return found

testlist = [1,2,32,8,17,19,42,13,0]
print(sequentialSearch(testlist,3)) # False
print(sequentialSearch(testlist,13)) # True

2. 顺序查找：有序表查找代码
当数据项存在时，查找有序表和无序表的方法完全相同。但是当数据项不在表中时，有序表可以提前结束。
算法复杂度仍然是O(n), 只是在数据项不存在的时候，有序表的查找能节省一些比对次数，但并不改变其数量级。

def sequentialSearch(alist, item):
    pos = 0
    found = False
    stop = False
    while pos < len(alist) and not found and not stop:
        if alist[pos] == item:
            found = True
        else:
            if alist[pos] > item:
                 stop = True  # 提前退出
        else:
            pos = pos + 1   # 下标顺序增长
   
    return found

testlist = [1,2,32,8,17,19,42,13,0]
print(sequentialSearch(testlist,3)) # False 只需要比对4次，少于无序表
print(sequentialSearch(testlist,13)) # True

二分法查找

二分法利用有序表的特性，缩小待比对数据项的范围。从列表中间开始比对，如果列表中间的项匹配查找项，则查找结束如果不匹配，那么就有两种情况：

• 列表查找项比中间项小，那么查找项只可能出现在前半部分
• 列表查找项比中间项大，那么查找项只可能出现在后半部分

无论如何，我们都会将比对范围缩小到原来的一半：n/2
继续采用上面的方法查找，每次都会将比对范围缩小一半

def binarySearch(alist, item):
    found = False
    first = 0
    last = len(thelist) - 1

    while first <= last and not found:
        midpoint = (first + last) // 2 # // 是除法取整数
        if alist[midpoint] == item:  # 中间项比对
            found = True  
        else:
            if item < alist[midpoint]:  # 缩小比对范围
                 last = midpoint - 1
            else first = midpoint + 1
    return found
    
testlist = [1,2,32,8,17,19,42,13,0]
print(sequentialSearch(testlist,3)) 
print(sequentialSearch(testlist,13))

二分查找算法实际上体现了解决问题的典型策略：分而治之

• 将问题分为若干更小规模的部分
• 通过解决每一个小规模部分问题，并将结果汇总得到原问题的解

二分查找的递归算法

def binarySearch(alist, item):
    if len(alist) == 0:
        return False  # 结束条件
    else:
        midpoint = len(alist) // 2 
        if alist[midpoint] == item:  # 中间项比对
            return True  
        else:
            if item < alist[midpoint]:  # 缩小规模
              return binarySearch(alist[:midpoint],item) #调用自身
            else:
              return binarySearch(alist[midpoint+1:],item)

当比对次数足够多以后，比对范围内就会仅剩余1个数据项
n / 2 ^ i = 1
i = $lo{g}_{2}n$
二分法查找的算法复杂度是O(log n)

另外，虽然二分查找在时间复杂度上优于顺序查找,但也要考虑到对数据项进行排序的开销。换句话说，二分查找需要先排序，会更麻烦一点。

冒泡排序和选择排序

冒泡排序Bubble Sort

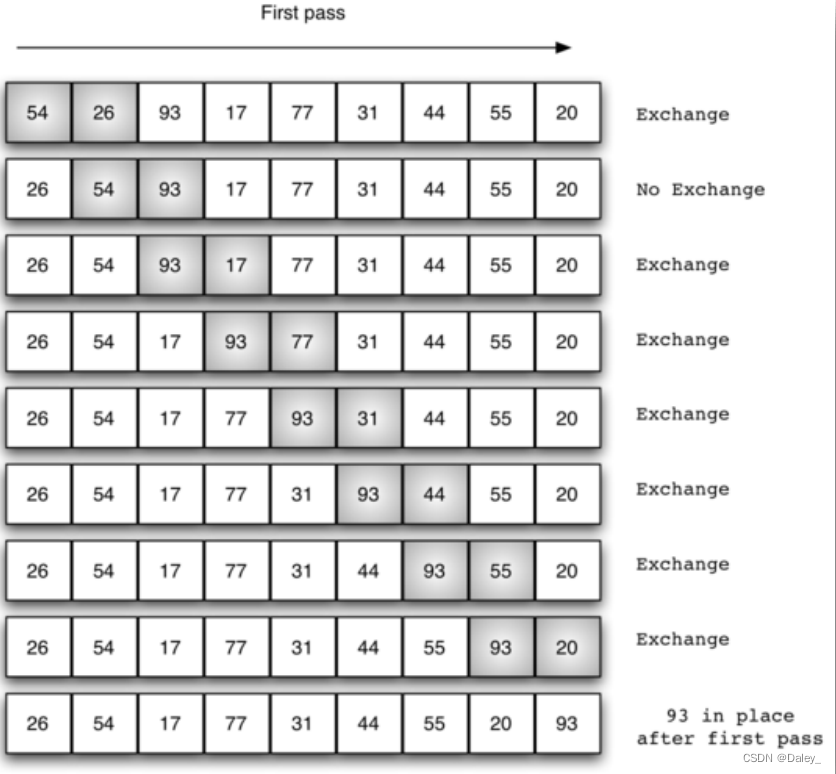
• 冒泡排序的算法思路在于对无序表进行多趟比较交换，每趟包括了多次两两相邻比较，并将逆序的数据项互换位置，最终能将本趟的最大项就位，经过n-1趟比较交换，实现整表排序。
• 第1趟比较交换，共有n-1对相邻数据进行比较，一旦经过最大项，则最大项会一路交换到达最后一项。
• 第2趟比较交换时，最大项已经就位，需要排序的数据减少为n-1，共有n-2对相邻数据进行比较，直到第n-1趟完成后，最小项一定在列表首位，就无需再处理了。
  

def bubbleSort(thelist):
    for i in range(len(thelist) - 1): # 一共有n - 1趟对比
        for j in range(len(thelist) - 1 - i): # 一趟对比n - i次
            if thelist[j] > thelist[j + 1]:
                temp = thelist[j]     
                thelist[j] = thelist[j + 1]
                thelist[j + 1] = temp
   # 交换值 也可以写成 alist[j],alist[j+1]=alist[j+1],alist[j]
alist = [54, 26, 93, 17, 77, 31, 44, 55, 20]
bubbleSort(alist)
print(alist)

算法分析：
一共对比n - 1趟
对比次数从n - 1 到 1次
对比的总次数是 1 + 2 +。。。 + n - 1 = $0.5n^2?0.5n$
时间复杂度是$O（n^2）$

• 最好的情况是列表在排序前已经有序，交换次数为0
• 最差的情况是每次比对都要进行交换，交换次数等于比对次数
• 平均情况则是最差情况的一半

冒泡排序通常作为时间效率较差的排序算法，来作为其它算法的对比基准。其效率主要差在每个数据项在找到其最终位置之前，必须要经过多次比对和交换，其中大部分的操作是无效的,但有一点优势，就是无需任何额外的存储空间开销。

冒泡排序：性能改进
加入变量检测排序过程是否出现交换，如果没有发生交换，说明已经排好序了，就不需要再进行下一趟的操作了。

def advancedBubbleSort(alist):
    exchanges = True
    passnum = len(alist)-1
    while passnum > 0 and exchanges:  
        exchanges = False   # 没有交换，可以停止，提前退出
        for i in range(passnum):
            if alist[i] > alist[i + 1]:
                temp = alist[i]
                alist[i] = alist[i + 1]
                alist[i + 1] = temp
        passnum = passnum + 1

alist = [54, 66, 93, 33, 22, 31, 44, 55, 20]
advancedBubbleSort(alist)
print(alist)

选择排序Selection Sort

• 选择排序对冒泡排序进行了改进，保留了其基本的多趟比对思路，每趟都使当前最大项就位。
• 但选择排序对交换进行了削减，相比起冒泡排序进行多次交换，每趟仅进行1次交换，记录最大项的所在位置，最后再跟本趟最后一项交换
• 选择排序的时间复杂度比冒泡排序稍优
  比对次数不变，还是O(n2)
  交换次数则减少为O(n)
  

def selectionSort(alist):
    for fillslot in range(len(alist) - 1, 0, -1): # 共比较n - 1 轮, range函数(a, b, c) a是开始，b是结束，c是步长
        maxpostion = 0
        for location in range(1, fillslot + 1): # 每轮比较n - i 对数据
            if alist[location] > thelist[maxpostion]:
                maxpostion = location # 找到这一轮的最大值的位置
        temp = alist[fillslot]
        alist[fillslot] = alist[maxpostion]
        alist[maxpostion] = temp

插入排序Insertion Sort

插入排序维持一个已排好序的子列表，其位置始终在列表的前部，然后逐步扩大这个子列表直到全表

• 第1趟，子列表仅包含第1个数据项，将第2个数据项作为“新项”插入到子列表的合适位置中，这样已排序的子列表就包含了2个数据项
• 第2趟，再继续将第3个数据项跟前2个数据项比对，并移动比自身大的数据项，空出位置来，以便加入到子列表中
• 经过n-1趟比对和插入，子列表扩展到全表，排序完成

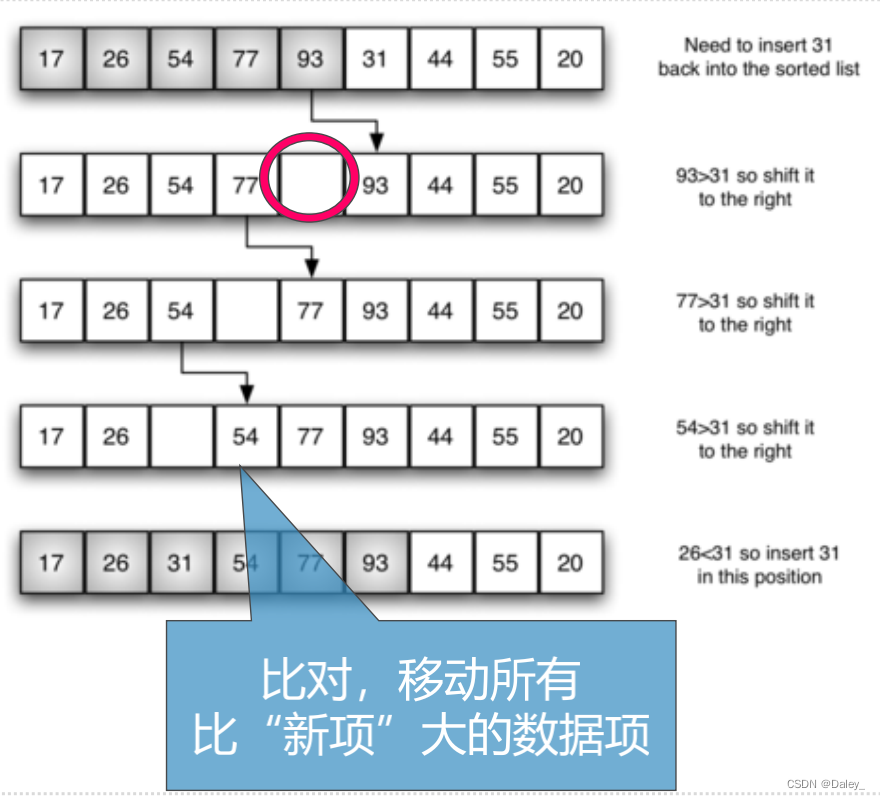
• 插入排序的比对主要用来寻找“新项”的插入位置
• 最差情况是每趟都与子列表中所有项进行比对，总比对次数与冒泡排序相同，数量级仍是$O(n^2)$
• 最好情况，列表已经排好序的时候，每趟仅需1次比对，总次数是$O(n)$

def insertionSort(alist):
    for index in range(len(alist) - 1):
        currentvalue = alist[index]  # 插入新项
        position = index
        while position > 0 and alist[position-1]>currentvalue:
            alist[position] = alist[position - 1] # 比对，移动
            position = position -1
            alist[position] = currentvalue # 插入新项

谢尔排序Shell Sort

• 我们注意到插入排序的比对次数，在最好的情况下是O(n)，这种情况发生在列表已是有序的情况下，实际上，列表越接近有序，插入排序的比对次数就越少。
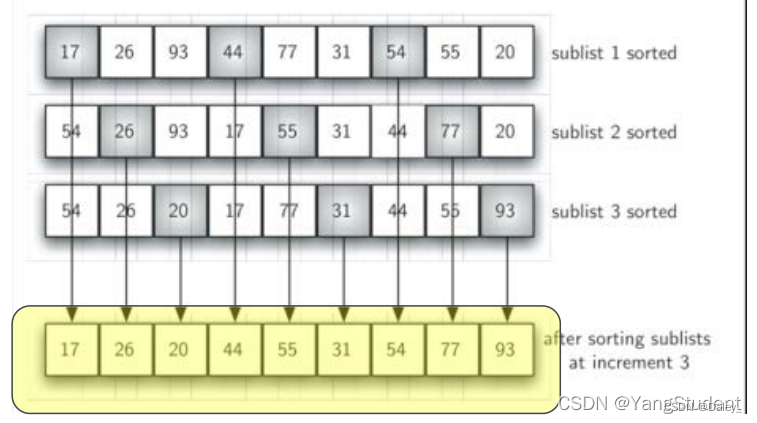
• 从这个情况入手，谢尔排序以插入排序作为基础，对无序表进行**“间隔”划分**子列表，每个子列表都执行插入排序。
• 随着子列表的数量越来越少，无序表的整体越来越接近有序，从而减少整体排序的比对次数，间隔为3的子列表，子列表分别插入排序后的整体状况更接近有序。
• 最后一趟是标准的插入排序，但由于前面几趟已经将列表处理到接近有序，这一趟仅需少数几次移动即可完成。
  

def shellSort(alist):
    sublistcount = len(alist)//2   # 设定子列表间隔
    while sublistcount > 0:
       
        for startposition in range (sublistcount):  # 子列表排序
            gapInsertionSort(alist,startposition,sublistcount)
        print("After increments of size",sublistcount,"the list is",alist)
       
        sublistcount = sublistcount//2   # 再次缩小间隔

def gapInsertionSort(alist,start,gap):  # 最后一次插入排序
    for  i in range(start+gap, len(alist),gap):
        # gap 是步长，新插入项
        currentvalue = alist[i]
        position = i

        while position >= gap and alist[position-gap]>currentvalue:
            # 对比，移动
            alist[position] = alist[position-gap]
            position = position-gap
   
        alist[position]=currentvalue       #插入新项

算法分析：

• 子列表的间隔一般从n/2开始，每趟倍增：n/4, n/8……直到1
• 谢尔排序以插入排序为基础，可能并不会比插入排序好。但由于每趟都使得列表更加接近有序，这过程会减少很多原先需要的“无效”比对。
  对谢尔排序的详尽分析比较复杂，大致说是介于$O(n)和O(n^2)$之间
• 如果将间隔保持在2^(k-1 ) (1，3，5，7，9等），
  谢尔排序的时间复杂度约为O ( n^ 3/2 )

归并排序Merge Sort

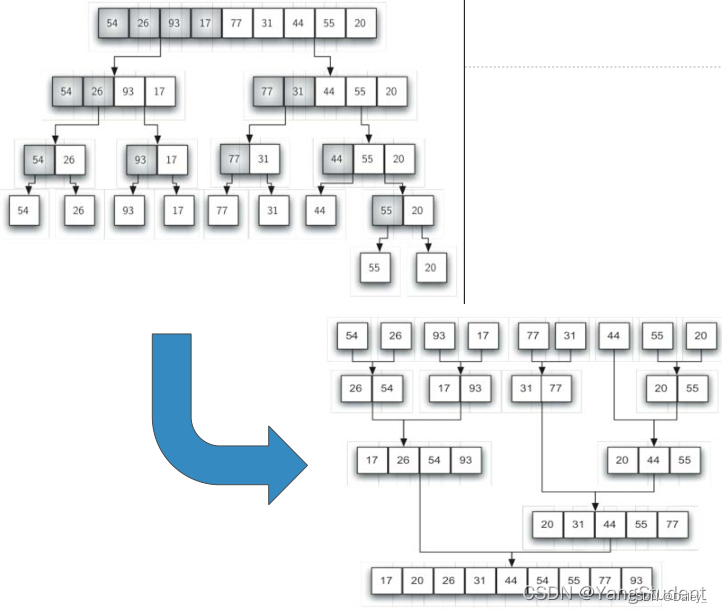
归并排序是递归算法，思路是将数据表持续分裂为两半，对两半分别进行归并排序

• 递归的基本结束条件是：数据表仅有1个数据项，自然是排好序的；
• 缩小规模：将数据表分裂为相等的两半，规模减为原来的二分之一；
• 调用自身：将两半分别调用自身排序，然后将分别排好序的两半进行归并，得到排好序的数据表。
  

def merge_sort(lst):
    # 递归结束条件
    if len(lst) <= 1:
        return lst
    # 分解问题，每次划分为原来的一半，并且递归调用
    mid = len(lst) // 2 # 中间点
    left = merge_sort(lst[: mid]) # 左半边归并
    right = merge_sort(lst[mid: ]) # 右半边归并

    # 合并左右半部，完成排序
    merged = []
    while left and right:
        if left[0] <= right[0]:
            merged.append(left.pop[0])
        else:
            merged.append(right.pop(0))

    merged.extend(right if right else left) # 把剩下的那半边一次性合并进去
    return merged

算法分析：

• 将归并排序分为两个过程来分析：分裂和归并
• 分裂的过程，借鉴二分查找中的分析结果，是对数复杂度，时间复杂度为$O(logn)$
• 归并的过程，相对于分裂的每个部分，其所有数据项都会被比较和放置一次，所以是线性复杂度，其时间复杂度是O(n)
  综合考虑，每次分裂的部分都进行一次O(n)的数
  据项归并，相乘起来，总的时间复杂度是$O(nlogn)$
• 我们注意到归并排序算法使用了额外1倍的存储空间用于归并。这个特性在对特大数据集进行排序的时候要考虑进去。

快速排序Quick Sort

-快速排序的思路是依据一个“中值”数据项来把数据表分为两半：小于中值的一半和大于中值的一半，然后每部分分别进行快速排序（递归）

• 如果希望这两半拥有相等数量的数据项，则应该找到数据表的“中位数”

• 但找中位数需要计算开销！要想没有开销，只能随意找一个数来充当“中值”，比如，第1个数。

• 分裂数据表的目标：找到“中值”的位置

• 分裂数据表的手段
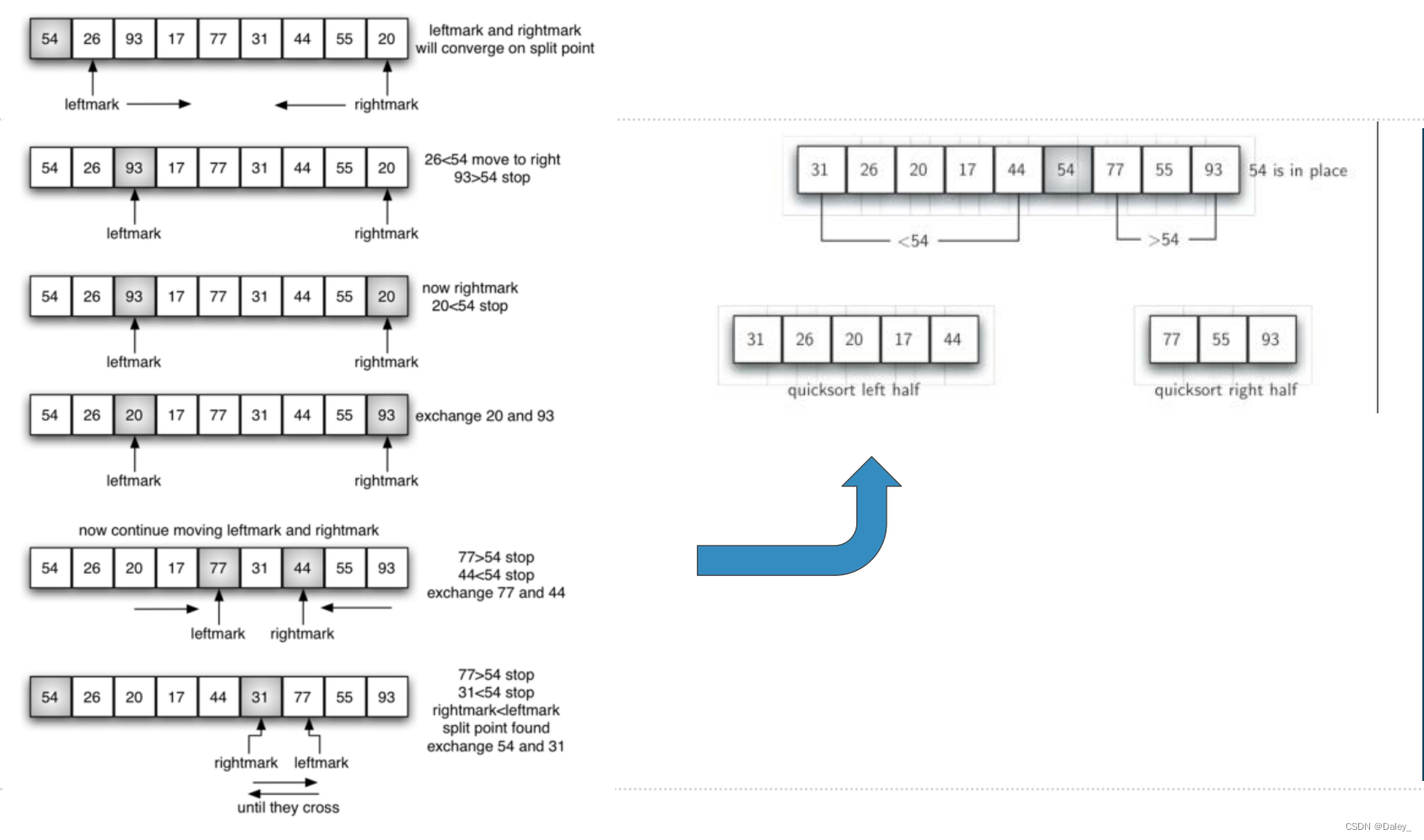
  1.设置左右标（left/rightmark）
  2.左标向右移动，右标向左移动
  ? 左标一直向右移动，碰到比中值大的就停止
  ? 右标一直向左移动，碰到比中值小的就停止
  ? 然后把左右标所指的数据项交换
  3.继续移动，直到左标移到右标的右侧，停止移动
  4.这时右标所指位置就是“中值”应处的位置，将中值和这个位置交换
  5.分裂完成，左半部比中值小，右半部比中值大
  

# 代码基本思路
def quickSortHelper(alist, first, last):
    if first < last:
        splitpoint = partition(alist, first, last)
        quickSortHelper(alist, first, splitpoint - 1)
        quickSortHelper(alist, splitpoint + 1, last)


def quickSort(alist):
    quickSortHelper(alist, 0, len(alist) - 1)

def partition(alist, first, last):
    # 选定“中值”
    pivotvalue = alist[first]
    # 左右标初值
    leftmark = first + 1
    rightmark = last

    done = False
    while not done:
        # 向右移动左标
        while leftmark <= rightmark and \
                alist[leftmark] <= pivotvalue:
            leftmark = leftmark + 1
        # 向左移动右标
        while rightmark >= leftmark and \
                alist[rightmark] >= pivotvalue:
            rightmark = rightmark - 1
        # 两标想错就结束移动
        if rightmark < leftmark:
            done = True
        else:
            # 左右标的值相互交换
            alist[leftmark], alist[rightmark] = alist[rightmark], alist[leftmark]

    # 中值就位
    alist[first], alist[rightmark] = alist[rightmark], alist[first]

    return rightmark

算法分析：

• 快速排序过程分为两部分：分裂和移动
• 如果分裂总能把数据表分为相等的两部分，那么就是O(log n)的复杂度；而移动需要将每项都与中值进行比对，还是O(n)，综合起来就是$O(nlogn)$；
• 算法运行过程中不需要额外的存储空间。
• 但是，如果不那么幸运的话，中值所在的分裂点过于偏离中部，造成左右两部分数量不平衡。极端情况：有一部分始终没有数据，这样时间复杂度就退化到$O(n^2)$,还要加上递归调用的开销（比冒泡排序还糟糕）。
• 可以适当改进下中值的选取方法，让中值更具有代表性。比如“三点取样”，从数据表的头、尾、中间选出中值，会产生额外计算开销，仍然不能排除极端情况。

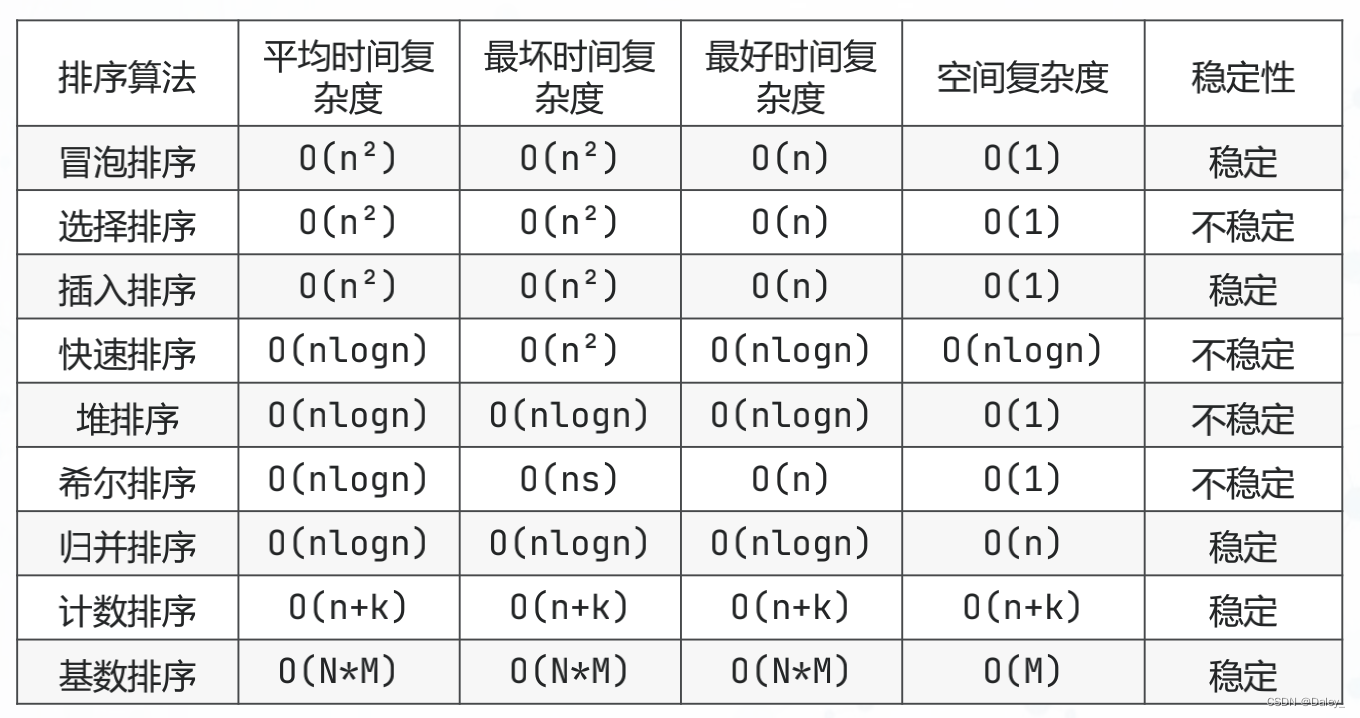
排序算法复杂度大全

散列Hashing

基本概念

1、散列
能使得查找算法的复杂度降到O(1)，这种概念称为“散列Hashing”。

2、散列表

• 散列表（hash table，又称哈希表）是一种数据集，其中数据项的存储方式尤其有利于将来快速的查找定位。
• 散列表中的每一个存储位置，称为槽（slot），可以用来保存数据项，每个槽有一个唯一的名称。

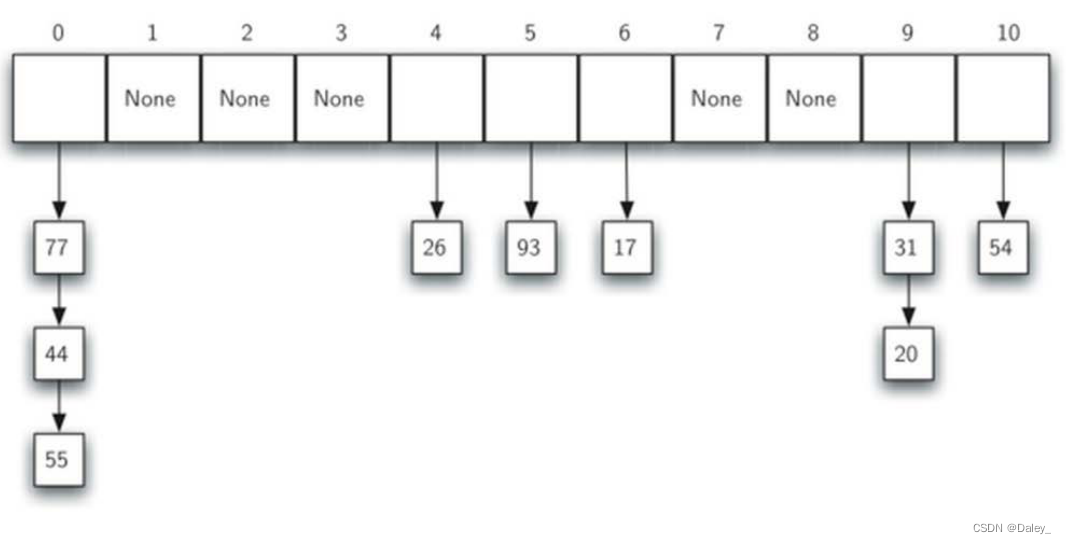
例如：一个包含11个槽的散列表，槽的名称分别为0～10
在插入数据项之前，每个槽的值都是None，表示空槽

3、散列函数
实现从数据项到存储槽名称的转换的，称为散列函数（hash function）。

4、常见的散列函数：求余散列

• 方法：
  将数据项除以散列表的大小，得到的余数作为槽号。
  实际上“求余数”方法会以不同形式出现在所有 散列函数里 因为散列函数返回的槽号必须在散列表大小范围 之内，所以一般会对散列表大小求余。
• 数据的查找：
  只需要使用同一个散列函数，对查找项进行计算，测试下返回的槽号所对应的槽中是否有 数据项即可
• 不足：
  可能会出现”冲突“现象。即：两个不同的数据项通过求余数后得到相同的槽号。

完美散列函数

• 给定一组数据项，如果一个散列函数能把每个数据项映射到不同的槽中，那么这个散列函数就可以称为“完美散列函数”。
• 获得完美散列函数的一种方法是扩大散列表的容量，大到所有可能出现的数据项都能够占据不同的槽，但这种方法对于可能数据项范围过大的情况并不实用。
• 因此，能做到冲突最少（近似完美）、计算难度低（额外开销小）、充分分散数据项（节约空间）就可以认定为好的散列函数。

散列的应用：区块链

• 区块链是一种分布式数据库，通过网络连接的节点 ，每个节点都保存着整个数据库所有数据任何地点存入的数据都会完成同步。
• 其本质特征：去中心化，即不存在任何控制中心，协调中心节点，所有节点都是平等的 ，无法被控制。
• 区块链由一个个区块（block）组成，区块分为头（head）和体（body）。 区块头记录了一些元数据和链接到前一个区块的信息：生成时间、前一个区块(head+body)的散列值。
• 区域链具有不可修改性：由于散列值具有抗修改性，任何对某个区块数据的改动必然引起散列值的变化，为了不导致这个区块脱离链条，就需要修改所有后续的区块。由于有“工作量证明”的机制，这种大规模修改 不可能实现的，除非掌握了全网51%以的计算力。

散列函数设计

1、折叠法
将数据项按照位数分为若干段，再将几段数字相加，最后对散列表大小求余，得到散列值。
有时候折叠法还会包括一个隔数反转的步骤；比如（62、76、72、55）隔数反转为（62、67、72、55），虽然隔数反转从理论上看来毫无必要，但这个步骤确实为折叠法得到散列函数提供了一种微调手段，以便更好符合散列特性。

2、平方取中（计算量稍大）
首先将数据项做平方运算，然后取平方数的中间两位，再对散列表的大小求余。

3、非数项
对非数字的数据项进行散列， 把字符串中的每个字符看作ASCII码即可，再将这些整数累加，对散列表大小求余。

如 cat, ord(‘c’) = 99, ord(‘a’) = 96, ord(‘t’) = 116 相加
cat == 99 + 96 +116 = 312
312 // 11 = 4

注意：
这样的散列函数对所有的变位词都 返回相同的散列值 为了防止这一点，可以将字符串所在的位置作为权重因子，乘以ord值。

c的位置是1，a的位置是2，t的位置是3
cat = 99 * 1 + 96 * 2 + 116 * 3 = 641
641 // 11 = 3

散列函数设计基本法则
1.散列函数不能太复杂，否则将成为存储过程和查找过程的计算负担。
2.散列值应尽可能地均匀分布

冲突解决方案

如果两个数据项被散列映射到同一个槽，需要一个系统化的方法在散列表中保存第二个数据项，这个过程称为“解决冲突”。

开放定址 open addressing

• 解决散列的一种方法就是为冲突的数据项再找一个开放的空槽来保存；最简单的就是从冲突的槽开始往后扫描，直到碰到一个空槽如果到散列表尾部还未找到，则从首部接着扫描。
• 向后逐个槽寻找的方法则是开放定址技术中的线性探测linear probing。

如：把44、55、20逐个插入到散列表中(除11求余）

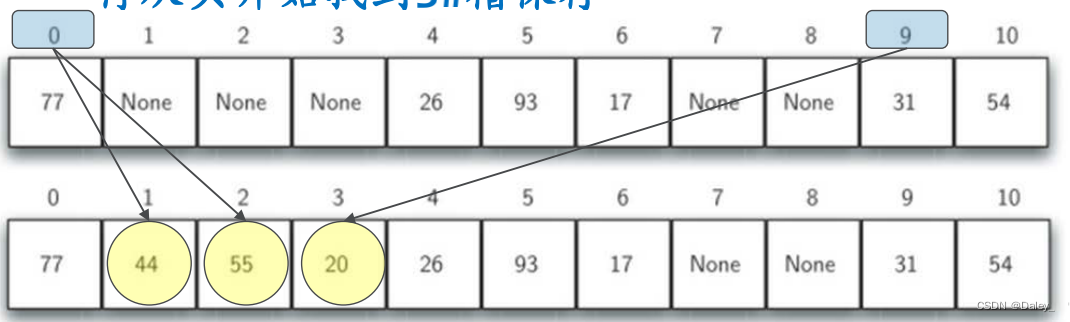
线性探测的改进
线性探测法的 一个缺点是有聚集 （clustering）的趋势；
如果同一个槽冲突的数据项较多的话，这些数据项就会在槽附近聚集起来从而连锁式影响其它数据项的插入，将逐个探测的方法改为跳跃探测。

下图是“+3”探测插入44、55、20

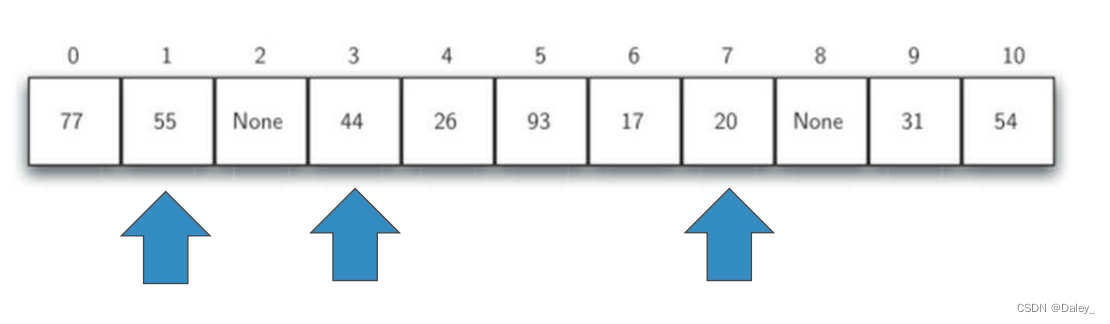
再散列
重新寻找空槽的过程可以用一个更为通用的“再散列rehashing”来概括：

newhashvalue = rehash(oldhashvalue)
对于线性探测来说，rehash(pos)= (pos+ 1)% sizeoftable
“+3”的跳跃式探测则是：rehash(pos)= (pos+ 3)% sizeoftable
跳跃式探测的再散列通式是：rehash(pos)= (pos+skip)% sizeoftable

跳跃式探测中，需要注意的是skip的取值，不能被散列表大小整除，否则会产生周期，造成很多空槽永远无法探测到一个技巧是，把散列表的大小设为素数，如例子的11，13，17，19

二次探测 quadratic probing
不再固定skip的值，而是逐步增加skip值，如1、3、5、7、9， 这样槽号就会是原散列值以平方数增加：h, h+1, h+4, h+9, h+16…

数据项链 Chaining

• 与开放地址不同，数据项链的散列表中，一个槽不止能存一个数据项，而是存数据项的集合。冲突发生时仍然存在那个槽里就行了。
• 查找某一个数据项时，就查找对应的槽里的数据项集合。如果冲突太多的话，查找的事件也会很长。
  

抽象数据类型“映射”:ADT Map

• 字典是一种可以保存key-data键值对的数据类型
  其中关键码key可用于查询关联的数据值data，这种键值关联的方法称为“映射Map”
• ADT Map的结构是键-值关联的无序集合
  关键码具有唯一性
  通过关键码可以唯一确定一个数据值

hashfunction方法采用了简单求余方法来实现散列函数，而冲突解决则采用**线性探测“加1”**再散列函数。

def hashfuction(self, key):
    return key %self.size

def rehash(self, oldhash):
    return (oldhash + 1) % self.size

def put(self, key, data):
    hashvalue = self.hashfunction(key)
    if self.slots[hashvalue] == None: #key不存在未冲突
        self.slots[hashvalue] = key
        self.data[hashvalue] = data
    else: #key已存在，替换val
        if self.slots[hashvalue] == key:
            self.data[hashvalue] = data  #replace
        else:
            nextslot = self.rehash(hashvalue)
            #散列冲突，再散列，直到找到空槽或者key
            while self.slots[nextslot] != None and self.slots[nextslot] != key:
                nextslot = self.rehash(nextslot)
            if self.slots[nextslot] == None:
                self.slots[nextslot] = key
                self.data[nextslot] = data
            else:
                self.data[nextslot] = data
                
def get(self,key):
    startslot = self.hashfunction(key) #标记散列值为查找起点
    data = None
    stop = False
    found = False
    position = startslot
    #找key,直到空槽或回到起点
    while self.slots[position] != None and not found and not stop:
        if self.slots[position] == key:
            found = True
            data = self.data[position]
        else:
            #未找到key,再散列继续找
            position = self.rehash(position)
            if position == startslot:
                stop = True
        return data

# 通过特殊方法实现[]访问   
def __getitem__(self,key):
    return self.get(key)

def __setitem__(self,key,data):
    self.put(key,data)

散列算法分析

1.散列在最好的情况下，可以提供O(1)常数级时间复杂度的查找性能。由于散列冲突的存在，查找比较次数就没有这么简单。

2.评估散列冲突的最重要信息就是负载因子λ，一般来说：
如果λ较小，散列冲突的几率就小，数据项通常会保存在其所属的散列槽中
如果λ较大，意味着散列表填充较满，冲突会越来越多，冲突解决也越复杂，也就需要更多的比较来找到空槽；如果采用数据链的话，意味着每条链上的数据项增多

3.如果采用线性探测的开放定址法来解决冲突（λ在0~1之间）
成功的查找，平均需要比对次数为： $ \frac{1}{2}(1 + \frac{1}{1 - λ}) $
失败的查找，平均需要比对次数为：$ \frac{1}{2}(1 + (\frac{1}{1 - λ})^2) $

4.如果采用数据链来解决冲突（λ可大于1）
成功的查找，平均需要比对次数为：1+λ/2
不成功的查找，平均比对次数为：λ

练习

1.快速排序主元

著名的快速排序算法里有一个经典的划分过程：我们通常采用某种方法取一个元素作为主元（中值），通过交换，把比主元小的元素放到它的左边，比主元大的元素放到它的右边。 给定划分后的N个互不相同的正整数的排列，请问有多少个元素可能是划分前选取的主元？

例如给定的排列是[1, 3, 2, 4, 5]。则：
1 的左边没有元素，右边的元素都比它大，所以它可能是主元；
尽管 3 的左边元素都比它小，但其右边的 2 比它小，所以它不能是主元；
尽管 2 的右边元素都比它大，但其左边的 3 比它大，所以它不能是主元；
类似原因，4 和 5 都可能是主元。
因此，有 3 个元素可能是主元。

输入格式:
一行数个整数的排列，由空格分隔

输出格式：
在第 1 行中输出有可能是主元的元素个数；在第 2 行中按递增顺序输出这些元素，其间以 1 个空格分隔，行首尾不得有多余空格。

输入样例：
1 3 2 4 5

输出样例：
3
1 4 5

时间限制：500ms内存限制：32000kb

方法1:对列表由小到大排序，再和原列表比对，比对成功的数字可以做主元

alist = list(map(int, input().split()))
newlist = sorted(alist)
pivot = []
for i in range(len(alist)):
    if alist[i] == newlist[i]:  # 如果为中值，则排序前后位置不变
        pivot.append(alist[i])
        
print(len(pivot))
pivot.sort()
print(" ".join(str(i) for i in pivot))

方法2:把列表中的第一位设置为最大，只要右边的数都比他大，就可以做主元，以此类推，进行循环

def compare(lst): #遍历第i个数n，左边都小于n，右边都大于n
    def comp(lst): 
        res=[]
        lstMax=lst[0]
        for i in range(len(lst)):
            if lst[i]>=lstMax:
                res.append(i)
                lstMax=lst[i]
        return res
    temp1=comp(lst)  #向右侧遍历、再向左侧遍历，时间复杂度为O（n）
    temp2=[len(lst)-i-1 for i in comp([-x for x in lst][::-1])][::-1]
    return  list(set(temp1) & set(temp2))
 
lst=[int(x) for x in input().split()]
ans=sorted(compare(lst))
print(len(ans))
print(' '.join([str(lst[i]) for i in ans]))

方法3:切片比较（好懂）

def prin_element(a):
    b = []
    if len(a) == 1:
        b = a
    else:
        for i in range(1,len(a)-1):
            if a[i] > max(a[:i]) and a[i] < min(a[i+1:]):
                b.append(a[i])
        if a[0] < min(a[1:]):
            b.insert(0,a[0])
        if a[-1] > max(a[:-1]):
            b.append(a[-1])
    print(len(b))
    print(' '.join([str(i) for i in b]))

lst = list(map(int,input().split()))
prin_element(lst)

2.第一个坏版本

现在有同一个产品的N个版本，编号为从1至N的整数；其中从某个版本之后所有版本均已损坏。现给定一个函数isBadVersion，输入数字N可判断该版本是否损坏（若损坏将输出True）；请找出第一个损坏的版本。
注：有时isBadVersion函数运行速度很慢，请注意优化查找方式

输入格式:
两行
第一行为整数，为产品号总数N
第二行为给定的判断函数，使用有效的Python表达式给出，可使用eval读取

输出格式：
一行数字，表示第一个损坏的版本

输入样例：
50
lambda n:n>=30

输出样例：
30

用例有运行时间限制，采取二分法来加快查找速度，注意当中间元素为损坏版本时，它也有可能是第一个损坏的版本

N = int(input())
isBadVersion = eval(input())

def firstBadVersion(n):
    first = 1
    last = n
    while first < last:    # 三种循环，不断缩小查找范围
        mid = (first + last) // 2
        if isBadVersion(mid):
            last = mid # 这里不能用mid-1，因为mid也有可能是第一个坏版本
        else:
            first = mid + 1
    return first

print(firstBadVersion(N))

3.插入与归并

给出如下定义：
插入排序是迭代算法，逐一获得输入数据，逐步产生有序的输出序列。每步迭代中，算法从输入序列中取出一元素，将之插入有序序列中正确的位置。如此迭代直到全部元素有序。

归并排序进行如下迭代操作：首先将原始序列看成 N 个只包含 1 个元素的有序子序列，然后每次迭代归并两个相邻的有序子序列，直到最后只剩下 1 个有序的序列。

现给定原始序列和由某排序算法产生的中间序列，请你判断该算法究竟是哪种排序算法？

输入格式:
两行由空格分隔的数字，其对应长度相等的列表
其中第一行代表未排序的列表，第二行是排序算法过程中某一步的中间列表

输出格式：
首先在第 1 行中输出Insertion Sort表示插入排序、或Merge Sort表示归并排序；然后在第 2 行中输出用该排序算法再迭代一轮的结果序列。题目保证每组测试的结果是唯一的。数字间以空格分隔，且行首尾不得有多余空格

输入样例：
3 1 2 8 7 5 9 4 0 6
1 3 2 8 5 7 4 9 0 6

输出样例：
Merge Sort
1 2 3 8 4 5 7 9 0 6

输入样例2：
3 1 2 8 7 5 9 4 6 0
1 2 3 7 8 5 9 4 6 0

输出样例2：
Insertion Sort
1 2 3 5 7 8 9 4 6 0

先观察插入排序后的列表，可以看出列表前一部分为有序列表，后一部分与插入排序前完全相同，通过这个特点判断是否为插入排序，否则为归并排序

def check(lst1,lst2):
    position = 0
    for i in range(len(lst1)-1):
        if lst2[i+1]<lst2[i]:
            position = i+1
            break
    if lst1[position:] == lst2[position:]: # 判断是否为插入排序
        lst2 = sorted(lst2[:position+1])+lst2[position+1:]
        print('Insertion Sort')
        print(' '.join([str(i) for i in lst2]))
    else: # 否则为归并排序
        cnt = 2
        lst = lst2
        while lst == lst2: # 对排序后的列表不断进行归并排序直到列表改变
            lst = [sorted(lst2[i:i+cnt]) for i in range(0,len(lst2),cnt)]
            lst = [num for sub_lst in lst for num in sub_lst]
            cnt *= 2
        print('Merge Sort')
        print(' '.join([str(i) for i in lst]))

lst1 = list(map(int,input().split()))
lst2 = list(map(int,input().split()))
check(lst1, lst2)

4.字符串中所有重排

给定一个字符串s与待查找字符串p，请给出使得s[i:i+len§]是p的一个字母重排的所有下标i；题目保证字符串p非空

输入格式:
两行字符串，第一行为s，第二行为p

输出格式：
所有满足条件的下标从小到大排列，以空格分隔输出
若无对应下标，则输出"none"

输入样例：
cbaebabacd
abc

输出样例：
0 6

将待查找字符串p和s[i:i+len§]排序后依次比对

def findAnagrams(s, p):
    p_rank = sorted(p)
    sub = []
    for i in range(len(s)-len(p)+1):
        s_rank = sorted(s[i:i+len(p)])
        if p_rank == s_rank:
            sub.append(i)
    if sub == []:
        print('none')
    else:
        print(' '.join([str(i) for i in sub]))


s = [i for i in input()]
p = [i for i in input()]
findAnagrams(s, p)

5.列表出现最频繁的元素

给定一个列表与数字K，按出现次数倒序输出列表中前K个出现最频繁的元素；若少于K个元素则返回所有元素

输入格式:
输入为两行
第一行为给定列表，以合法的Python表达式给出
第二行为数字K

输出格式：
不多于K个数字，以空格分隔

输入样例：
[1,1,1,2,2,3]
2

输出样例：
1 2

def topKFrequent(nums, k):
    dct = {}
    for x in nums:
        dct[x] = dct.get(x, 0) + 1
        # 取key=x的值，如果没有就设置为0
    result = sorted(dct.items(), key=lambda x: -x[1])
    # 将数字及其重复次数组成的元组，按照-x[1],即次数倒序排序
    result = [x[0] for x in result[:k]]
    print(*result)
 
 
lst = eval(input())
k = int(input())
topKFrequent(lst, k)

6.散列表

给定一个指定大小N的散列表，并输入一系列数字：若找到空槽，则插入该数字，并返回槽位置；若该数字在散列表中存在，则直接输出其位置。
注：使用下标增加的二次探测法解决散列冲突
注2：散列表实际大小应确定为不小于用户输入N的最小质数

输入格式:
两行
第一行为用户指定散列表大小N
第二行为一系列数字，以空格分隔

输出格式：
逐个输出对应数字在散列表中位置，以空格分隔
若该数字无法插入，则输出“-”

输入样例：
4
10 6 4 10 15

输出样例：
0 1 4 0 -

def createHashTable(n):
    # 这里需要找出不小于n的最小质数
    if n==1 or n==2:
        slots = 2
    else:
        for i in range(2, n):
            if n % i == 0:
                n = n + 1
        else:
            slots = n
    table = {x:None for x in range(slots)} # 初始化哈希表
    return table      

def insertNumbers(table, nums):
    # 逐个将数字填入hash table，并保存其位置就可以了
    length = len(table)
    for i in range(len(nums)):
        num = nums[i]
        key = num % length
        if table[key] == None:
            table[key] = num
            nums[i] = key
        elif table[key] == num:
            nums[i] = key
        else:
            nums[i] = "-"
    print(" ".join(str(x) for x in nums))

N = int(input())
nums = list(map(int, input().split()))
table = createHashTable(N)
insertNumbers(table, nums)