1916.?统计为蚁群构筑房间的不同顺序
你是一只蚂蚁,负责为蚁群构筑?
n?间编号从?0?到?n-1?的新房间。给你一个?下标从 0 开始?且长度为?n?的整数数组?prevRoom?作为扩建计划。其中,prevRoom[i]?表示在构筑房间?i?之前,你必须先构筑房间?prevRoom[i]?,并且这两个房间必须?直接?相连。房间?0?已经构筑完成,所以?prevRoom[0] = -1?。扩建计划中还有一条硬性要求,在完成所有房间的构筑之后,从房间?0?可以访问到每个房间。你一次只能构筑?一个?房间。你可以在?已经构筑好的?房间之间自由穿行,只要这些房间是?相连的?。如果房间?
prevRoom[i]?已经构筑完成,那么你就可以构筑房间?i。返回你构筑所有房间的?不同顺序的数目?。由于答案可能很大,请返回对?
109 + 7?取余?的结果。示例 1:
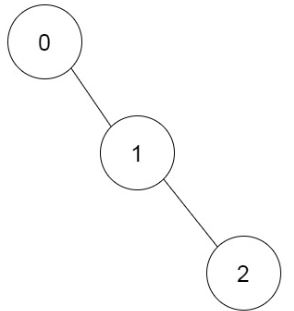
输入:prevRoom= [-1,0,1] 输出:1 解释:仅有一种方案可以完成所有房间的构筑:0 → 1 → 2示例 2:
输入:prevRoom= [-1,0,0,1,2] 输出:6 解释: 有 6 种不同顺序: 0 → 1 → 3 → 2 → 4 0 → 2 → 4 → 1 → 3 0 → 1 → 2 → 3 → 4 0 → 1 → 2 → 4 → 3 0 → 2 → 1 → 3 → 4 0 → 2 → 1 → 4 → 3提示:
n == prevRoom.length2 <= n <= 105prevRoom[0] == -1- 对于所有的?
1 <= i < n?,都有?0 <= prevRoom[i] < n- 题目保证所有房间都构筑完成后,从房间?
0?可以访问到每个房间来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/longest-univalue-path
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
做题结果
失败,方法完全对,但是不掌握组合数用的费马小定理,就搞不定。1e5的话,不可以用杨辉三角算。上次偷懒没学,这次也不算完全懂,但是会用了
方法:快速幂+费马小定理+DFS
1. 费马小定理用在组合数怎么用(因为找了很多资料,还是看不懂,最后大概通过结论猜出怎么用),单从组合数而言,(1/a)%MOD当做 (a^(MOD-2)) 处理
2. 阶乘:x! 这个简单吧,循环连乘即可,用 inv[i]表示。1/(k!) 可以用费马小定理搞定 用fac[i]表示
3. 组合公式? ,我们已知 n!,1/(m!),1/(n-m)!,也就是inv[n]*fac[m]*fac[n-m]
,我们已知 n!,1/(m!),1/(n-m)!,也就是inv[n]*fac[m]*fac[n-m]
4.?a^(MOD-2)) 需要用到快速幂。快速幂简单的数就是折半幂的过程。比如 2^10,我们可以看成是(2^2)^5,然后遇到5,需要单独拆出一个,变成 (2^2)*(2^2)^4=(2^2)*((2^2)^2)^2,这样可以大大减少计算次数,乘法,加法,减法过程可以求余数,防止溢出
private long pow(long a, long b){
long ans = 1L;
while (b>0){
if((b&1)==1){
ans = ans*a%MOD;
}
b=b/2;
a= a*a%MOD;
}
return ans;
}5. DFS: 先排好一个子树,假设这个子树本身有 x1 个节点,有 y1 种排法,然后第二个子树的元素,实际上是插入前面元素的空格。比如原本有 x2个节点,则要把这x2个插入 x1+x2的空位之中,然后现在已有节点数目就变成 x1+x2,又当前子树有 y2种排法 y1*c(x1+x2,x2)*y2*c(x1+x2+x3,x3)*y3.....,算完所有子树后即可得到最终结果
class Solution {
long[] fac;
long[] inv;
public int waysToBuildRooms(int[] prevRoom) {
//1.建图
Map<Integer,Set<Integer>> graph = new HashMap<>();
int n = prevRoom.length;
for(int i = 1;i < n; i++){
graph.computeIfAbsent(prevRoom[i],o->new HashSet<>()).add(i);
}
fac = new long[n];
inv = new long[n];
fac[0]=inv[0]=1;
for(int i = 1; i < n; i++){
fac[i] = fac[i-1]*i%MOD;
inv[i] = pow(fac[i],MOD-2);
}
return (int) dfs(graph,-1,0)[0];
}
private long pow(long a, long b){
long ans = 1L;
while (b>0){
if((b&1)==1){
ans = ans*a%MOD;
}
b=b/2;
a= a*a%MOD;
}
return ans;
}
long ans = 0L;
final long MOD = (long) (1e9+7);
//摆法+节点
private long[] dfs(Map<Integer,Set<Integer>> graph, int pre, int index){
if(!graph.containsKey(index) || (graph.size()==1&&graph.containsKey(pre))){
return new long[]{1,1};
}
int total = 0;//总共选了几个点
long ans = 1L;
for(int next:graph.get(index)){
if(next==pre) continue;
long[] item = dfs(graph,index,next);
long c = getC((int)(total+item[1]),(int)item[1]);
ans = ans * c%MOD*item[0]%MOD;
total+=item[1];
}
return new long[]{ans,total+1};
}
private long getC(int a, int b){
return fac[a]*inv[a-b]%MOD*inv[b]%MOD;
}
}