[数据结构与算法]c++ 关于bfs和dfs的相对统一写法

简介

• 有向图bfs
• 有向图dfs
• 有向图拓扑排序

着重看看bfs 和 dfs 实现的差异性， 了解二者的相似和不同

代码

#include <iostream>
#include <vector>
#include <algorithm>
#include <chrono>
#include <stack>
#include <queue>
#include <numeric>

using namespace std;

struct Edge {
    int to;
    int weight;
};

struct Vertex {
    vector<Edge> adjacent;
};

// 无向图
class Graph {
public:
    int n{};
    vector<Vertex> nodes;

protected:
    [[nodiscard]] virtual Graph *clone() const {
        return new Graph(*this);
    }

public:
    Graph() = default;

    Graph(const Graph &other) {
        this->n = other.n;
        this->nodes = other.nodes;
    }

    virtual void addEdge(int v, int w, int weight = 0) {
        nodes[v].adjacent.push_back({.to = w, .weight = weight});
        nodes[w].adjacent.push_back({.to = v, .weight = weight});
    }

    void addAllEdge(int n, vector<vector<int>> &edges) {
        this->n = n;
        nodes.resize(n);
        for (auto &vec: edges) {
            int from = vec[0];
            int to = vec[1];
            int weight = 0;
            if (vec.size() >= 3) {
                weight = vec[2];
            }
            addEdge(from, to, weight);
        }
    }

    [[nodiscard]] int Vex() const {
        return n;
    }

    [[nodiscard]] const vector<Edge> &getEdges(int v) const {
        return nodes[v].adjacent;
    }

    [[nodiscard]] virtual Graph *reverse() const {
        auto g = this->clone();
        return g;
    }

};

// 有向图
class DiGraph : public Graph {
public:
    DiGraph() = default;

    [[nodiscard]] Graph *reverse() const override {
        Graph* g = new DiGraph;
        g->n = this->n;
        g->nodes.resize(g->n);

        for (int from = 0; from < Vex(); from++) {
            for (auto &e: getEdges(from)) {
                int to = e.to;
                int weight = e.to;
                g->addEdge(to, from, weight);
            }
        }
        return g;
    }

    void addEdge(int v, int w, int weight) override {
        nodes[v].adjacent.push_back({.to = w, .weight = weight});
    }

private:
    [[nodiscard]] Graph *clone() const override {
        return new DiGraph(*this);
    }
};

class QAbs {
public:
    virtual void enQ(int id) = 0;

    virtual int deQ() = 0;

    virtual bool empty() = 0;
};

class DfsQ : public QAbs {
private:
    stack<int> q;

public:
    void enQ(int id) override {
        q.push(id);
    }

    int deQ() override {
        int id = q.top();
        q.pop();
        return id;
    }

    bool empty() override {
        return q.empty();
    }
};

class BfsQ : public QAbs {
private:
    queue<int> q;
public:
    void enQ(int id) override {
        q.push(id);
    }

    int deQ() override {
        int id = q.front();
        q.pop();
        return id;
    }

    bool empty() override {
        return q.empty();
    }
};

enum class Order {
    BFS = 0,
    DFS = 1,
};

class TraversalAbs {
public:
    Graph *g;
    vector<bool> known;
    QAbs *q;

protected:
    virtual void pre(int v) {
        cout << v << "\t";
    }

    virtual void afterOneTraversal() {
        cout << endl;
    }

    virtual void afterTraversal() {
    }

public:
    TraversalAbs(Graph *g, Order order) : g(g), known(g->Vex()) {
        if (order == Order::BFS) {
            q = new BfsQ;
        } else {
            q = new DfsQ;
        }
    }

    void traversal(int v) {
        known[v] = true;
        q->enQ(v);
        while (!q->empty()) {
            int id = q->deQ();
            // 先序
            pre(id);
            for (auto w: g->getEdges(id)) {
                int to = w.to;
                if (known[to]) {
                    continue;
                }
                known[to] = true;
                q->enQ(to);
            }
        }
        afterOneTraversal();
    }

    void traversal() {
        for (int i = 0; i < g->Vex(); i++) {
            if (known[i]) {
                continue;
            }
            traversal(i);
        }
        afterTraversal();
    }
};

class DfsTopology : public TraversalAbs {
public:
    explicit DfsTopology(Graph *g) : TraversalAbs(g, Order::DFS) {}

private:
    stack<int> st;
    stack<int> ans;

protected:
    void pre(int v) override {
        st.push(v);
    }

    void afterTraversal() override {
        while (!ans.empty()) {
            cout << ans.top() << "\t";
            ans.pop();
        }
        cout << endl;
    }

    void afterOneTraversal() override {
        while (!st.empty()) {
            ans.push(st.top());
            st.pop();
        }
    }
};


int main() {
    vector<vector<int>> data = {
            {0, 1, 2},
            {1, 2, 2},
            {2, 3, 1},
            {3, 4, 2},
            {0, 4, 3},
    };
    auto g = new DiGraph;
    g->addAllEdge(5, data);

    auto rg = g->reverse();

    // bfs 遍历
    TraversalAbs btr(g, Order::BFS);
    btr.traversal(0);

    // dfs 遍历
    TraversalAbs dtr(g, Order::DFS);
    dtr.traversal(0);

    // 拓扑排序
    auto df = new DfsTopology(rg);
    df->traversal();
}

输出

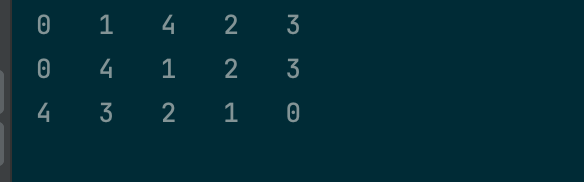
c++ 关于bfs和dfs的相对统一写法
c++ 关于bfs和dfs的相对统一写法
c++ 关于bfs和dfs的相对统一写法
c++ 关于bfs和dfs的相对统一写法
c++ 关于bfs和dfs的相对统一写法
c++ 关于bfs和dfs的相对统一写法
c++ 关于bfs和dfs的相对统一写法
c++ 关于bfs和dfs的相对统一写法
c++ 关于bfs和dfs的相对统一写法
c++ 关于bfs和dfs的相对统一写法