[数据结构与算法]LeetCode算法入门与九月打卡

算法入门

第1天 二分查找

704. 二分查找

class Solution {
    public int search(int[] nums, int target) {
        //设置左右指针
        int left = 0;
        int right = nums.length - 1;
        //遍历数组
        while(left <= right){
            //获取中间位置
            int mid = (left + right) >> 1;
            if(nums[mid] == target){
                return mid;
            }else if(nums[mid] < target){
                left = mid + 1;
            }else{
                right = mid - 1;
            }
        }
        //返回结果
        return -1;
    }
}

278. 第一个错误版本

public class Solution extends VersionControl {
    public int firstBadVersion(int n) {
        if(n == 1){
            return 1;
        }
        int left = 1;
        int right = n;
        while(left < right){
            //因为left + right 可能存在溢出
            int mid = left + (right - left) / 2;
            if(!isBadVersion(mid)){
                left = mid + 1;
            }else{
                right = mid;
            }
        }
        return right;
    }
}

35. 搜索插入位置

class Solution {
    public int searchInsert(int[] nums, int target) {
        //设置左右指针
        int left = 0;
        int right = nums.length - 1;
        //两个特殊位置
        if(target < nums[left]){
            return left;
        }
        if(target > nums[right]){
            return right + 1;
        }
        //遍历数组
        while(left < right){
            int mid = left + (right - left) / 2;
            //找到了
            if(nums[mid] == target){
                return mid;
            }else if(nums[mid] < target){
                left = mid + 1;
            }else{
                //取右边这个为插入位置
                right = mid;
            }
        }
        //没找到
        return right;
    }
}

第2天 双指针

977. 有序数组的平方

利用一个新数组来维护结果，利用双指针的方式，从原数组两端找出绝对值较大的数放到新数组的末尾，直至遍历完整数数组，最后将数组的值变为原来的平方

class Solution {
    public int[] sortedSquares(int[] nums) {
        //设置双指针
        int left = 0;
        int right = nums.length - 1;        
        //保存结果数组
        int [] res = new int[nums.length];
        //遍历原数组，从后向前添加
        for(int i = 0; i < nums.length && left <= right; i++){
            res[nums.length - 1 - i] = Math.abs(nums[left]) > Math.abs(nums[right]) ?
            Math.abs(nums[left++]) : Math.abs(nums[right--]);
        }
        //调用方法
        square(res);
        //返回结果
        return res;
    }
    //平方处理
    public void square(int [] nums){
        for(int i = 0; i < nums.length; i++){         
            nums[i] = (int)Math.pow(nums[i], 2);
        }
    }
}

189. 轮转数组

整体翻转 + 局部翻转

class Solution {
    public void rotate(int[] nums, int k) {
        //可能翻转好几圈
        k = k % nums.length;
        //整体翻转 + 局部翻转
        reverse(nums, 0, nums.length - 1);
        reverse(nums, 0, k - 1);
        reverse(nums, k, nums.length - 1);
    }
    //根据给定的索引翻转
    public void reverse(int [] nums, int start, int end){
        while(start < end){
            //交换
            int temp = nums[start];
            nums[start] = nums[end];
            nums[end] = temp;
            //更新
            start++;
            end--;
        }
    }   
}

第3天 双指针

283. 移动零

利用双指针从左向右遍历，将非零数按照出现的顺序排序，最后所有零都自然的排到了数组的末尾

class Solution {
    public void moveZeroes(int[] nums) {
        //利用双指针，将所有非零元素移动到数组的前面
        int left = 0;
        int right = 0;
        //数组只有一个元素
        if(nums.length == 1){
            return ;
        }
        //遍历数组
        while(right < nums.length){
            if(nums[right] != 0){
                int temp = nums[right];
                nums[right] = nums[left];
                nums[left] = temp;
                //移动左指针
                left++;
            }
            //移动右指针
            right++;
        }
    }
}

167. 两数之和 II 输入有序数组

可以用两数之和的哈希表解法,牺牲时间换内存

因为数组是有序的，所以利用双指针来解决更方便

class Solution {
    public int[] twoSum(int[] numbers, int target) {
        //设置左右指针
        int left = 0; 
        int right = numbers.length - 1;
        //遍历数组
        while(left < right){
            //当前左右指针的元素和
            int sum = numbers[left] + numbers[right];
            if(sum == target){
                return new int []{++left, ++right};
            }else if(sum > target){
                right--;
            }else{
                left++;
            }
        }
        return new int[]{-1, -1};
    }
}

第4天 双指针

344. 反转字符串

class Solution {
    public void reverseString(char[] s) {
        //只有一个元素
        if(s.length == 1){
            return ;
        }
        //设置双指针
        int start = 0;
        int end = s.length - 1;
        while(start < end){
            //交换两侧的字符
            char temp = s[start];
            s[start] = s[end];
            s[end] = temp;
            //移动双指针
            start++;
            end--;
        }
    }
}

557. 反转字符串中的单词

遍历字符串，通过一个指针来找到所有片段，从后向前添加每个片段的字符，根据指针的位置添加空格【此处采用的StringBuilder是线程不安全的】

class Solution {
    public String reverseWords(String s) {
        //只有一个字符
        if(s.length() == 1){
            return s;
        }
        //保存结果
        StringBuilder sb = new StringBuilder();
        //遍历字符串
        int i = 0;
        while(i < s.length()){
            //找到非空格片段
            int start = i;
            while(i < s.length() && s.charAt(i) != ' '){
                i++;
            }
            //将这部分逆序添加到结果串中
            for(int j = start; j < i; j++){
                sb.append(s.charAt(start + i - 1 - j));
            }
            //添加空格
            if(i < s.length() && s.charAt(i) == ' '){
                i++;
                sb.append(" ");
            }
        }
        //返回结果
        return sb.toString();
    }
}

解法2： 下面是通过分割获取每个片段的长度

class Solution {
    public String reverseWords(String s) {
        //只有一个字符
        if(s.length() == 1){
            return s;
        }
        //拼接结果字符串
        StringBuffer sb = new StringBuffer();
        //分割获得每部分的长度
        String [] str = s.split(" ");
        //设置索引
        int index = 0;
        for(int i = 0; i < s.length(); ){
            int len = str[index].length();
            for(int j = 0; j < len; j++){
                //从每部分的末尾开始添加
                sb.append(s.charAt(i + len - 1 - j));
            }
            //补充空格
            if(index < str.length - 1 ){
                sb.append(" ");
            }
            //移动到下一个片段的开头
            i = i + len + 1;
            index++;
            
        }
        //返回结果
        return sb.toString();
    }
}

第5天 双指针

867. 链表的中间结点

可以通过 快慢指针 来完成，快指针每次走两步，慢指针每次走一步，当快指针走到尽头，慢指针就到达了链表的中点。

重点在于临界条件的处理，快指针最后有两种状态：

指向链表的最后一个元素【链表元素为奇数个】
指向空 【链表元素为偶数个】

所以临界条件应该为 fast != null && fast.next != null

class Solution {
    public ListNode middleNode(ListNode head) {
        //设置快慢指针
        ListNode fast = head;
        ListNode slow = head;
        //遍历链表
        while(fast != null && fast.next != null){
            slow = slow.next;
            fast = fast.next.next;
        }
        //返回结果
        return slow;
    }
}

19. 删除链表的倒数第N个结点

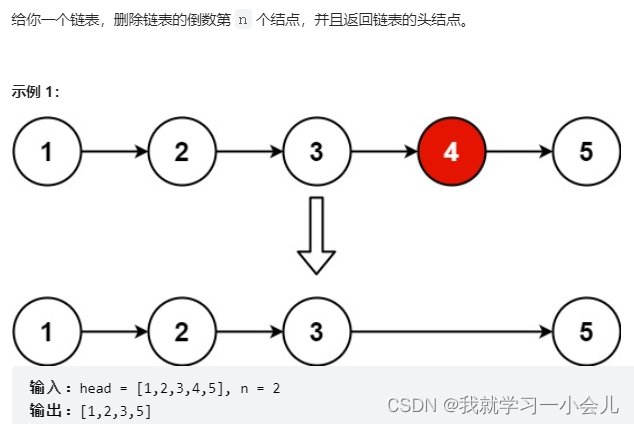
遍历一次链表，统计链表的结点个数，判断是否要删除第一个结点，是则直接返回链表的第二个结点，否则就遍历寻找待删除结点的前驱结点，删除后返回链表头结点

要注意，此题链表的头结点指的是链表的第一个结点

class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
        //记录链表结点的个数
        int count = 0;
        ListNode p = head;
        while(p != null){
            count++;
            p = p.next;
        }
        //待删除的结点为第一个结点
        if(count == n){
            return head.next;
        }
        //遍历到待删除结点的前驱结点
        ListNode pre = head;
        for(int i = 0; i < count - n - 1; i++){
            pre = pre.next;
        }
        //删除结点
        pre.next = pre.next.next;
        //返回结果
        return head;
    }
}

第6天 滑动窗口

3. 无重复字符最长子串

利用 HashMap 来存储字符串中的元素与出现的位置，每遍历一个元素，就将其添加到哈希表中，Key 为字符 —— Value 为元素当前的位置。

利用滑动的窗口来记录不重复子串的长度，left 定义为左边界。
当哈希表中存在了当前的字符，那么就更新左边界的位置，此时分为两种情况：

left = Math.max(left, map.get(ch) + 1);

（1）找到上次出现该字符的位置，将左边界移动到该位置的右边
（2）可能移动后的位置在当前左边界的左边，如果这样就不更新左边界

记录最大无重复子串的长度maxLen = Math.max(maxLen, i - left + 1);

class Solution {
    public int lengthOfLongestSubstring(String s) {
        //字符串长度为零
        if(s.length() == 0){
            return 0;
        }
        //设置哈希表，记录元素与对应的位置
        Map<Character, Integer> map = new HashMap<Character, Integer>();
        //设置滑动窗口左边界
        int left = 0;
        //记录最大长度
        int maxLen = 0;
        //遍历字符串
        for(int i = 0; i < s.length(); i++){
            //获取当前字符
            char ch = s.charAt(i);
            //判断是否存在于map中
            if(map.containsKey(ch)){
                //更新左边界，第一次出现ch的位置+1，如果更新后的边界小于现在的左边界则不更新
                left = Math.max(left, map.get(ch) + 1);
            }
            //将当前字符添加到map中[已经存在了就更新索引位置]
            map.put(ch, i);
            //更新最大长度
            maxLen = Math.max(maxLen, i - left + 1);
        }
        //返回结果
        return maxLen;
    }
}

567. 字符串的排列

• 滑动窗口的大小就是 s1 的大小
• 遍历字符串，在 s2 中截取和窗口长度相同大小的子串
• 调用方法通过两个字符串的组成是否相同来比较。【固定窗口大小】

class Solution {
    public boolean checkInclusion(String s1, String s2) {
        //滑动窗口的大小
        int left = 0;
        int right = s1.length();
        //保存结果
        boolean res = false;
        //遍历字符串s2
        while(right <= s2.length()){
            //判断当前窗口是否符合条件
            res = isSame(s1, s2.substring(left, right));
            if(res){
                break;
            }
            left++;
            right++;
        }
        return res;

    }
    //判断两个字符串的组成是否相同
    public boolean isSame(String s1, String s2){
        //记录每个字母出现的次数
        int [] num = new int[26];
        //遍历s2串
        for(int i = 0; i < s2.length(); i++){
            char c = s2.charAt(i);
            num[c - 'a']++;
        }
        //遍历s1串
        for(int j = 0; j < s1.length(); j++){
            char ch = s1.charAt(j);
            if(--num[ch - 'a'] < 0){
                return false;
            }
        }
        return true;
    }
}

九月打卡

9月1日

1475. 商品折扣后的最终价格

class Solution {
    public int[] finalPrices(int[] prices) {
        //双层for循环
        for(int i = 0; i < prices.length; i++){
            for(int j = i + 1; j < prices.length; j++){
                if(prices[j] <= prices[i]){
                    prices[i] -= prices[j];
                    break;
                }
            }
        }
        return prices;
    }
}

9月2日

687. 最长同值路径

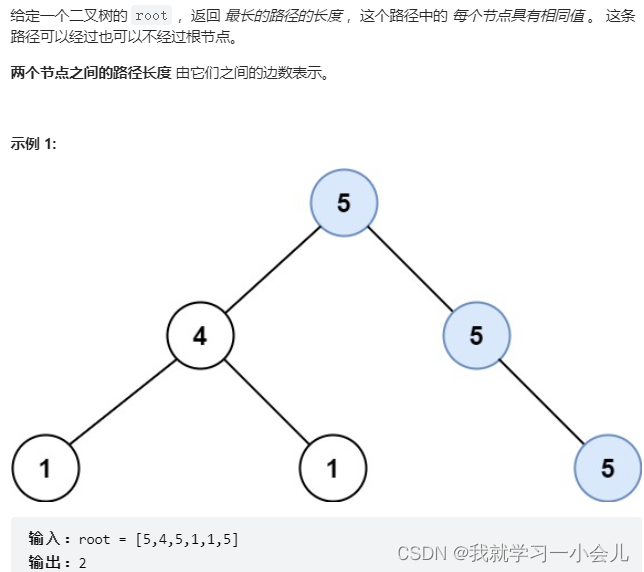
利用 深度优先搜索，自底向上 的思想，记录当前结点左、右结点的最长同值路径。当前结点的最长同值路径是其左右结点的最长同值路径的和。利用全局变量来记录结果。

注意：dfs返回的值应该是左子树或右子树的最长路径，因为一条路径不会出现分叉。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int res = 0;
    public int longestUnivaluePath(TreeNode root) {
        //深度优先搜索
        dfs(root);
        //返回结果
        return res;

    }
    public int dfs(TreeNode root){
        //当前结点为空
        if(root == null){
            return 0;
        }
        //获得当前结点的左右子树
        int left = dfs(root.left);
        int right = dfs(root.right);

        //判断满足条件的左子树
        if(root.left != null && root.left.val == root.val){
            left++;
        }else{
            left = 0;
        }
        //判断满足条件的右子树
        if(root.right != null && root.right.val == root.val){
            right++;
        }else{
            right = 0;
        }
        //统计最长同值路径
        res = Math.max(res, left + right);
        //返回结果
        return Math.max(left, right);
    }

}

9月3日

646. 最长数对链

• 先根据每行的第一个元素进行排序【使用Arrays的sort方法、自己设计一个排序方法】

（1）方法一：

Arrays.sort(pairs, (a, b) -> a[0] - b[0]);

这个方法实际后面的部分是 一个实现接口的内部类，写成了Lambda表达式
如果换为 b[0] - a[0],则是逆序排序
如果将 0 换为 1 ，则是根据每行的第二个与元素进行排序

（2）方法二：【采用的是冒泡排序】

for(int i = 0; i < pairs.length - 1; i++){
	for (int j = 0; j < pairs.length - 1 - i; j++) {
		if(pairs[j][0] > pairs[j + 1][0]){
			int [] temp = pairs[j];
			pairs[j] = pairs[j + 1];
			pairs[j + 1] = temp;
		} 
	}
}

• 利用动态规划，设置 dp 数组 【dp[i] 代表以第pairs[i] 结尾时的最大对数链】
• 对数链至少有一个，所以将数组初始化为1

Arrays.fill(dp, 1);

• 动态转移 【j < i】

dp[i] = Math.max(dp[i], dp[j] + 1)

class Solution {
    public int findLongestChain(int[][] pairs) {
        //按照每行第一个元素升序排序
        Arrays.sort(pairs, (a,b) -> a[0] - b[0]);
        //行数
        int n = pairs.length;
        //设置dp数组
        int[] dp = new int[n];
        //初始化
        Arrays.fill(dp, 1);
        for (int i = 0; i < n; i++) {
            //当前考虑的为第0行到第i行的最大对数链
            for (int j = 0; j < i; j++) {
                //满足条件
                if (pairs[i][0] > pairs[j][1]) {
                    //更新
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }
            }
        }
        //返回结果
        return dp[n - 1];
    }
}