排序算法
排序算法分类
- 内部排序:将需要处理的所有数据加载到内部存储器种进行排序
- 插入排序
- 直接插入排序
- 希尔排序
- 选择排序
- 简单选择排序
- 堆排序
- 交换排序
- 冒泡排序
- 快速排序
- 归并排序
- 基数排序
- 插入排序
- 外部排序:当数据量过大,无法全部加载到内存,需要使用外部存储进行排序
排序涉及到的问题
时间复杂度:度量一个程序执行时间的方法
- 事后统计方法—方法可行,但是很难保证算法执行时间,因为涉及到的硬件、软件等环境因素很难保证一致
- 事前估算方法—通过分析算法的时间复杂度来判断哪个更优秀
如何估算时间复杂度?
时间频度:一个算法花费的时间与算法中语句执行的次数成正比例,哪个算法中语句执行次数多,那么它花费的时间就越多。一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)
比如进行计算从1到100的数列和,使用for循环
int sum=0;
int n=100;
for (int i = 1; i <= n; i++) {// 将执行n+1次因此T(n)=n+1
sum+=i;
}
除此之外,计算数列和还可以直接使用公式
sum=(1+n)*n/2 //无论n多大,只需要执行一次所以T(n)=1
注意:
- T(n)在统计时,可以忽略常数项,因为当n不足够大时,时间上的差异时很难体现的,当n足够大时,常数项又可以忽略不计,因此T(n)通常会忽略常数项。比如T(n)=n+10,我们通常说T(n)=n
- T(n)在统计时,可以忽略低次项,比如T(n)= n 2 n^2 n2+2n+10,当n增加时,越来越接近T(n)= n 2 n^2 n2
- T(n)在统计时,可以忽略系数,比如T(n)=4 n 2 n^2 n2+2n+10和T(n)=5 n 2 n^2 n2+2n+10,我们可以看作T(n)= n 2 n^2 n2
f(n)为辅助函数,当n趋于无穷大,T(n)/f(n)的极限值为不等于0的常数,那么称F(n)是T(n)的同数量级函数。记作T(n)=O(f(n)),称O(f(n))为算法的渐进时间复杂度,简称时间复杂度。时间复杂度只是表示这个算法在n增加时,执行所需要的时间增加的一种趋势。
T(n)不同,但是时间复杂度可能相同,比如T(n)= n 2 n^2 n2+2n+10与T(n)=3 n 2 n^2 n2+n+6它们的T(n)不同,但是时间复杂度相同都是O(n2)。
计算时间复杂度的方法
- 用常数1代替运行时间中的所有加法常数 T(n)=3 n 2 n^2 n2+n+6—>T(n)=3 n 2 n^2 n2+n+1
- 运行次数函数只保留最高阶项 T(n)=3 n 2 n^2 n2+n+1—>T(n)=3 n 2 n^2 n2
- 去掉最高阶项的系数 T(n)=3 n 2 n^2 n2—>T(n)=n^2—>O(n2)
常见的时间复杂度
-
常数阶 O(1)
无论代码执行多少行,只要没有循环等复杂结构,那么时间复杂度都是O(1)
int sum=0; int n=100; -
对数阶 O( l o g 2 n log_2n log2?n)
在循环中,每次都将i乘以2,那么i离n越来越近。假设执行x次后i大于n,也就是说2的x次方等于n,那么x= l o g 2 n log_2n log2?n,也就是说循环 l o g 2 n log_2n log2?n次后就退出循环,时间复杂度就是O( l o g 2 n log_2n log2?n)
int n=100; int i=1; while(i<n) { i=i*2; } -
线性阶O(n)
单纯的一个for循环就是线性阶
int sum=0; int n=100; for (int i = 0; i < n; i++) { sum+=i; } -
线性对数阶O( n l o g 2 n nlog_2n nlog2?n)
一个for循环里面嵌套一个while循环
for (int i = 0; i < n; i++) { sum=1; while(i<n){ i=i*2; } } -
平方阶O( n 2 n^2 n2)
两重执行n次的循环
for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) { sum++; } }如果外循环执行m次,内循环n次,那么时间复杂度就是O(m*n)
-
立方阶O( n 3 n^3 n3)
-
k次方阶O( n k n^k nk)
-
指数阶O( 2 n 2^n 2n)
说明:
- 常见的算法时间复杂度从小到大1->2->3->4->5->6->7->8
- 尽量避免使用指数阶的算法
平均时间复杂度
平均时间复杂度是指所有可能的输入实例以均等概率出现的情况下,运行该算法的时间
最坏时间复杂度
最坏时间复杂度是指最坏的情况下,运行该算法的时间,最坏时间复杂度保证了算法运行时间的界限,不会比最坏情况更长。
注意:平均时间复杂度和最坏时间复杂度是否一致和算法有关
空间复杂度:度量一个程序执行所需要的空间
常用排序算法的时间复杂度与空间复杂度
| 排序算法 | 平均时间 | 最差情况 | 稳定度 | 额外空间 | 备注 |
|---|---|---|---|---|---|
| 冒泡 | O( n 2 n^2 n2) | O( n 2 n^2 n2) | 稳定 | O(1) | n小时较好 |
| 交换 | O( n 2 n^2 n2) | O( n 2 n^2 n2) | 不稳定 | O(1) | n小时较好 |
| 选择 | O( n 2 n^2 n2) | O( n 2 n^2 n2) | 不稳定 | O(1) | n小时较好 |
| 插入 | O( n 2 n^2 n2) | O( n 2 n^2 n2) | 稳定 | O(1) | 大部分已排序时较好 |
| 基数 | O( l o g R B log_R B logR?B) | O( l o g R B log_R B logR?B) | 稳定 | O(n) | B是真数(0-9) R是基数(个十百) |
| 快速 | O( n l o g n nlogn nlogn) | O( n 2 n^2 n2) | 不稳定 | O( n l o g n nlogn nlogn) | n大时较好 |
| 归并 | O( n l o g n nlogn nlogn) | O( n l o g n nlogn nlogn) | 稳定 | O(1) | n大时较好 |
| 堆 | O( n l o g n nlogn nlogn) | O( n l o g n nlogn nlogn) | 不稳定 | O(1) | n大时较好 |
冒泡排序
冒泡排序是最基础的排序,冒泡就是将不符合规定顺序的相邻元素进行调换,一轮一轮的将数字移动到合适的位置。
冒泡排序就像水底的气泡从水下往上冒一样,数据会根据排序次数的增加越接近自己本身应该在的位置。
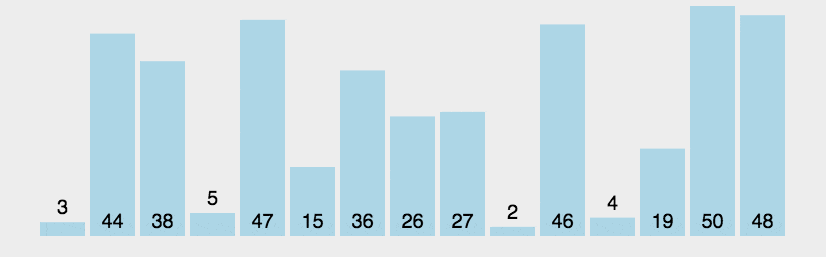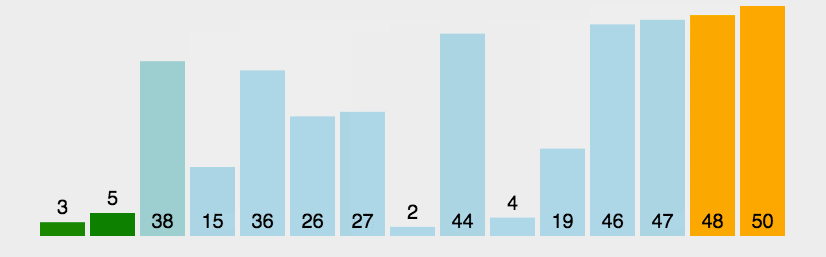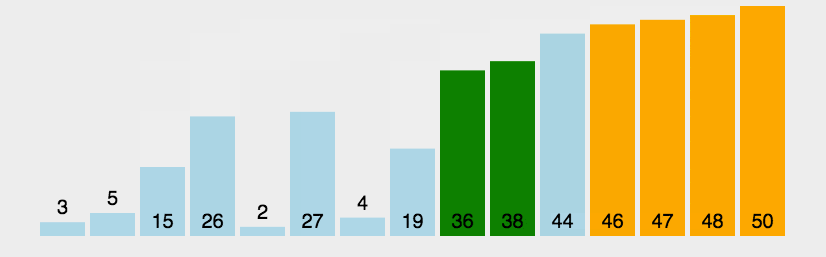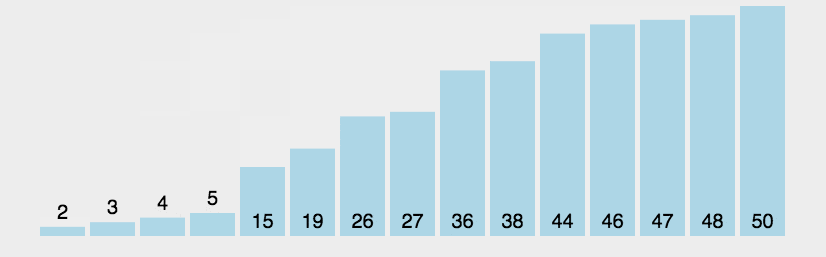
比如从小到大排序
for(int i=0;i<n;i++){
for(int j=0;j<n-i-1;j++){
if(a[j]>a[j+1]){
temp=a[j];
a[j]=a[j+1];
a[j+1]=temp;
}
}
}
第一轮循环会将最大的数移动到最后,第二轮会将第二大的数移动到最大的数前,以此类推,实际上随着循环轮数的增加,每轮循环执行的次数也在减少。假设一共长度为n第一轮循环结束,那么就有1个有序的数,n-1个无序的,无序的数随着循环论数增加而减少,每执行一轮,无序的数量-1,这就是为什么j<n-i-1的原因。
冒泡排序的优化:
因为可能会出现进行到某一轮循环时,并没有发生数据的交换,此时表明这个数组中的数据已经符合规定的顺序,那么下面的循环就没有必要继续了,可以减少不必要的比较。
使用布尔类型的flag进行判断
boolean flag=false;//判断是否进行交换
for(int i=0;i<n;i++){
for(int j=0;j<n-i-1;j++){
if(a[j]>a[j+1]){
temp=a[j];
a[j]=a[j+1];
a[j+1]=temp;
flag=true;//flag=true代表进行了交换
}
}
if(flag){//如果进行了交换就将flag初始化为false,如果没有就直接退出
flag=false;
}else {
break;
}
}
选择排序
选择排序的思想是将数据分成两部分,排序部分和未排序部分。比如从小到大进行选择排序,就先在未排序部分找到最小元素,然后跟第一个元素交换,此时第一个元素就变成了排序部分。重复这个步骤,从剩余的未排序元素中找到最小元素,然后跟未排序序列的第一个元素(也就是已排序部分的末尾的下一个元素)进行交换。
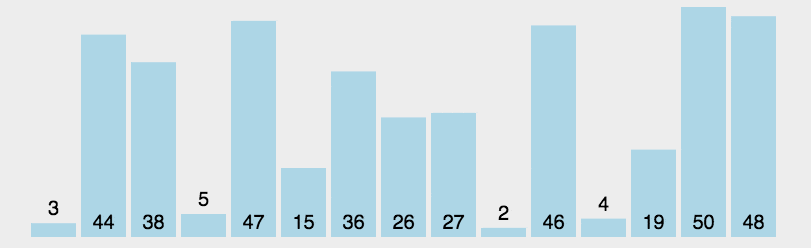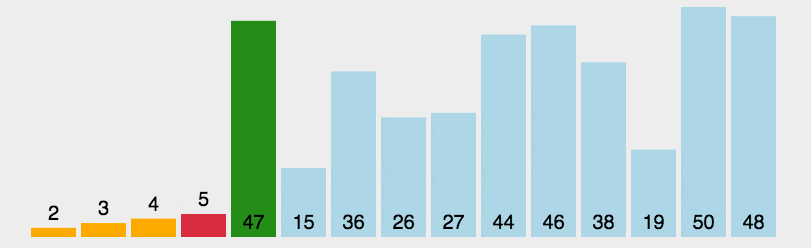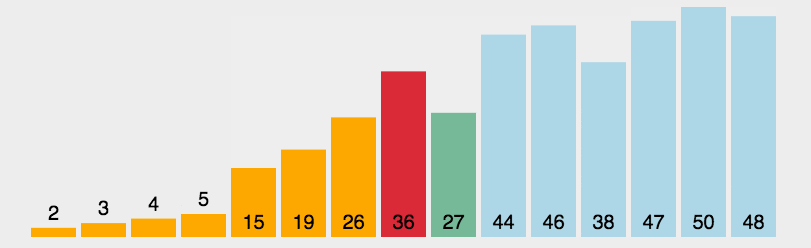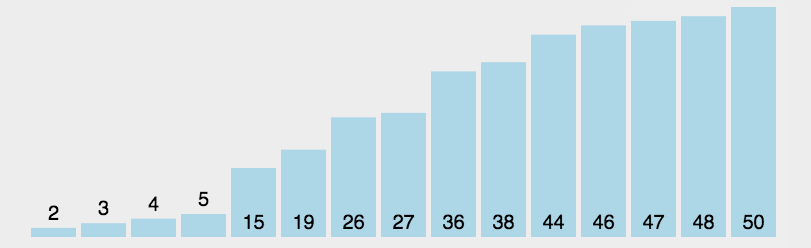
int a[]={1,8,3,2,5};
int temp=0;//记录最小值
int index=0;//下标
int n=a.length;
for(int i=0;i<n-1;i++){
temp=a[i];
index=i;
for(int j=i+1;j<n;j++){
//找到最小值,并保存最小值的下标
if(temp>a[j]){
temp=a[j];
index=j;
}
}
//最小的和未排序的第一个进行交换
if(index!=i){//当最小的不是未排序的第一个元素时,进行交换,是的话就不用交换了
a[index]=a[i];
a[i]=temp;
}
}
实际上代码还可以简化成不记录最小值的情况
// 总共要经过 N-1 轮比较
for (int i = 0; i < arr.length - 1; i++) {
int min = i;
// 每轮需要比较的次数 N-i
for (int j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[min]) {
// 记录目前能找到的最小值元素的下标
min = j;
}
}
// 将找到的最小值和i位置所在的值进行交换
if (i != min) {
int tmp = arr[i];
arr[i] = arr[min];
arr[min] = tmp;
}
}
插入排序
插入排序的思想是将n个待排序的元素看成一个有序部分和无序部分,刚开始有序部分只有一个元素,无序部分有n-1个元素,排序过程是每次从无序表取出第一个元素然后把它跟有序表中的元素进行比较,插入有序表适当的位置,使其成为新的有序表。
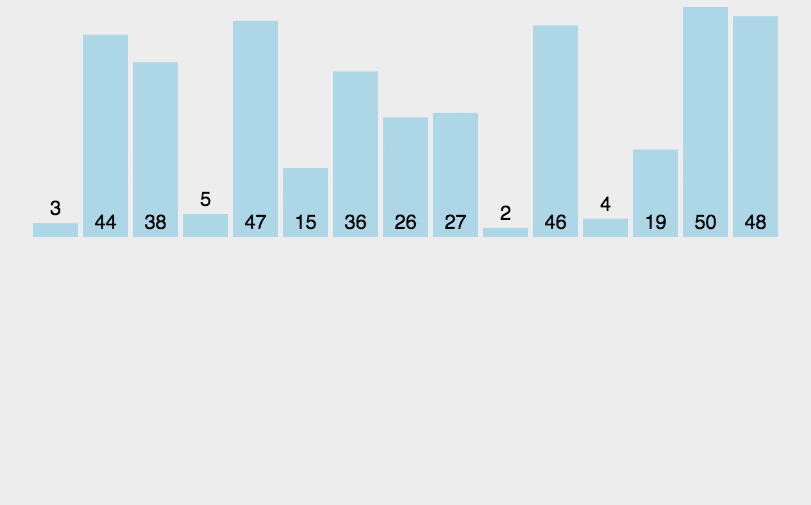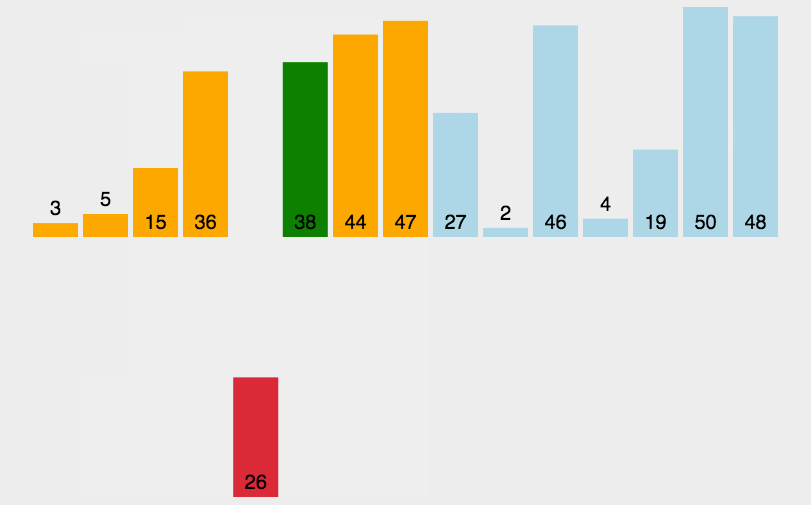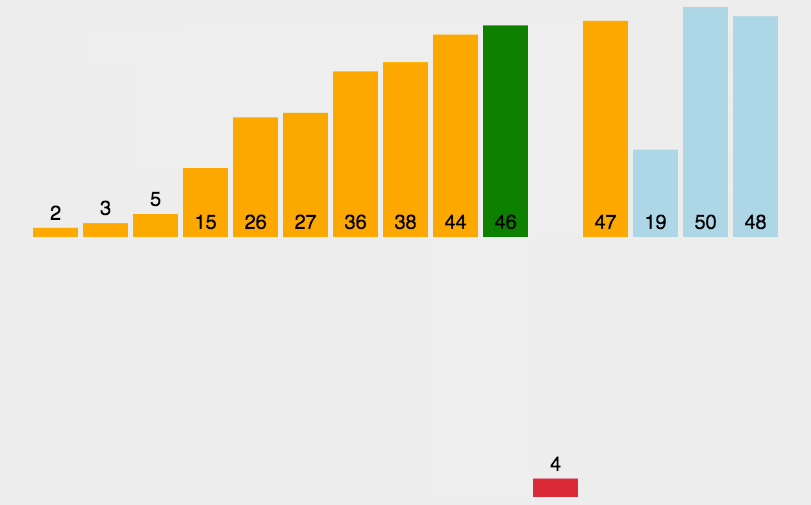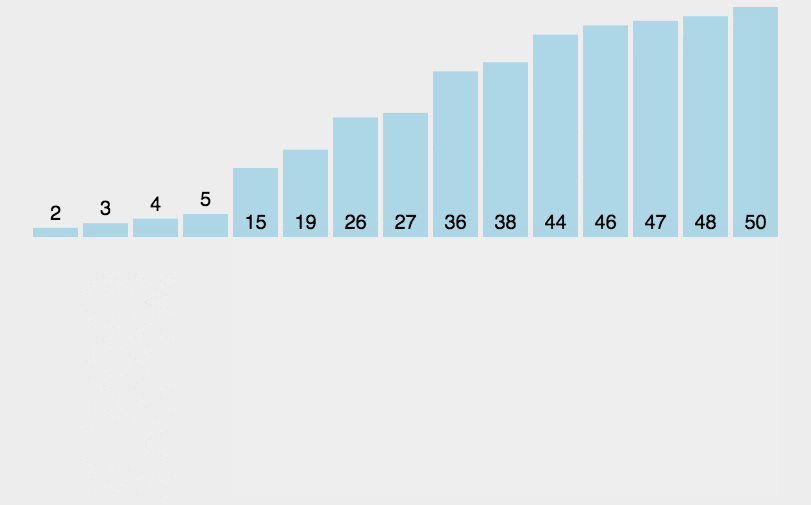
for(int i=1;i<n;i++){
int insertNum=a[i];//无序列表的第一个元素,使用insertNum进行保存它的值,后面会因为移动有序部分而覆盖该位置的值
int index=i-1;//无序列表的第一个元素的前一个元素,也就是有序列表的最后一个元素的位置
/*
index>=0是为了防止数组越界
insertNum<a[index]是为了找到插入的位置,如果insertNum大于a[index]那么说明已经找到了合适的位置
*/
while(index>=0&&insertNum<a[index]){
a[index+1]=a[index];//因为将index位置的值往后移,因为要将insertNum移到合适的位置,所以先将有序部分的其他元素往后移一位,相当于覆盖插入元素的位置
index--;//索引往前移动,查询新的位置是否符合要求
}
a[index+1]=insertNum;//因为经过while循环之后index的位置代表的是有序部分a[index]<insertNum,所以index的后一个位置就是insertNum应该插入的位置
}
希尔排序
希尔排序是在简单插入排序基础上进行改进得到的排序算法,也称为缩小增量排序(增量为数据的组数,从 n / 2 n/2 n/2到1,数据组数为1时意味着进入排序的最后阶段)。

交换法
int a[]={8,9,1,7,2,3,5,4,6,0};
int temp=0;
int n=a.length;
int step=n/2;//步长为总长度一半
while(step>=1){//当步长等于1说明已经是最后一次排序,那么排序完成就退出循环即step<1
for(int i=step;i<n;i++){//循环
for(int j=i-step;j>=0;j-=step){//j从0开始,每执行一次就将j减去步长,如果小于0说明已经没有需要比较的元素了
if(a[j]>a[j+step]){//j跟j+step位置的值比较,如果j位置的值大于j+step位置的值就交换
temp=a[j];
a[j]=a[j+step];
a[j+step]=temp;
}
}
}
step=step/2;
}
注意:j-=step是因为当步长减小时,每一个组内的数据在增加,数据之间实际上也是无序的,仅仅进行两两交换是不足以让组内所有数据都有序的,所以需要再进行排序。
比如当进行到第二轮时数组是3,5,1,6,0,8,9,4,7,2
i=2,那么j=0,a[j]>a[j+step]发生交换,交换一次j-step<0就退出j所在的循环
1,5,3,6,0,8,9,4,7,2
i++,进行下一次循环,此时j=1,因为j+step=3,a[j]<a[j+step]因此不交换,j-step<0退出j所在循环
1,5,3,6,0,8,9,4,7,2
i++,进行下一次循环,此时j=2,j+step=4,a[j]>a[j+step]发生交换
1,5,0,6,3,8,9,4,7,2
然后j-=step=0,此时j+step=2,a[j]>a[j+step]发生交换
0,5,1,6,3,8,9,4,7,2
此时再进行j-=step,j就小于0,退出该循环。
所以j-=step就是在后面排序时,在第一次跟j后面的j+step位置进行比较之后,再将j往前移一个步长,比较j和j+step的顺序是否一致,实际上就是将j+step位置的元素移动到前面以step为步长的有序部分的合适的位置。
移动法
int a[]={8,9,1,7,2,3,5,4,6,0};
int n=a.length;
int step=n/2;//步长为总长度一半
while(step>=1){//当步长等于1说明已经是最后一次排序,那么排序完成就退出循环即step<1
for(int i=step;i<n;i++){//循环
int j=i;
int temp=a[j];
if(a[j]<a[j-step]){
while(j-step >=0&&temp<a[j-step]){
a[j]=a[j-step];
j-=step;
}
a[j]=temp;
}
}
step=step/2;
}
移动法实际上就是对分组后的数据进行插入排序,将无序部分数据一个一个的插入有序部分中合适的位置。
快速排序
快速排序的思想是1.在无序的序列中找到一个数作为基准base(基准可以为第一个数、最后一个数、中间值等有很多种取法,这里将基准取为中间值)。2.找到基准后将小于基准的数移到左边,大于基准的数移到右边,此时无序序列中就形成了以基准为分割,左小右大的一个序列,此时两边的序列还是无序的,只需要左右分别递归调用算法即可,即在左边重复1,2步骤,右边重复1,2步骤,最后就会得到一个有序的序列。
public static void quickSort(int arr[],int left,int right){
int l=left;//左下标
int r=right;//右下标
int pivot=arr[(left+right)/2];//中值
while(l<r){//将比中值小的放在左边,大的放在右边
while(arr[l]<pivot){//找到一个大于基准值的就退出
l++;
}
while (arr[r]>pivot){//找到一个小于基准值的就退出
r--;
}
if(l>=r){//说明左右两边已经满足左小右大,就不需要交换了
break;
}
int temp=arr[r];//将两个值交换
arr[r]=arr[l];
arr[l]=temp;
if(arr[l]==pivot){//当交换之后arr[l]==pivot,说明l不需要再往后移动直接让r往前移一个位置,再进行比较
r--;
}
if(arr[r]==pivot){//当交换之后arr[r]==pivot,说明r不需要再往前移动直接让l往后移一个位置,再进行比较
l++;
}
}
//如果l==r,要将l++,r--,不然会出现栈溢出
if(l==r){
l++;
r--;
}
if(left<r){//左递归
quickSort(arr,left,r);
}
if(right>l){//右递归
quickSort(arr,l,right);
}
}
整个交换过程为:
a[]={8,9,1,7,2,3,5,4,6,0};
中值为2,整体划分,将比2小的放左边,比2大的放右边
第1次交换0 9 1 7 2 3 5 4 6 8
第2次交换0 2 1 7 9 3 5 4 6 8
第3次交换0 1 2 7 9 3 5 4 6 8
当进行完第一次排序,right=9,left=0
r=1,l=3
此时左右无序,进行递归,
left-r为左边部分,l-right为右边部分
0-1左递归,3-9右递归
此时基准为5,将4 9 3 5 7 6 8进行左小右大划分
第1次交换 4 9 3 5 7 6 8
第2次交换 4 5 3 9 7 6 8
第3次交换 4 3 5 9 7 6 8
此时再重复步骤,分成两部分,4 3左递归
第1次交换3 4
重复步骤,5 9 7 6 8右递归,重复找基准,左小右大
第1次交换5 6 7 9 8
重复步骤,因为左边5 6已经有序,所以不发生交换,右边9 8进行递归发生交换
第1次交换8 9
此时递归完成整个序列就变成了 0 1 2 3 4 5 6 7 8 9
归并排序
归并排序利用经典的分治策略,将问题分成小的问题进行递归求解。

分的步骤很容易理解,但是治的步骤比较复杂
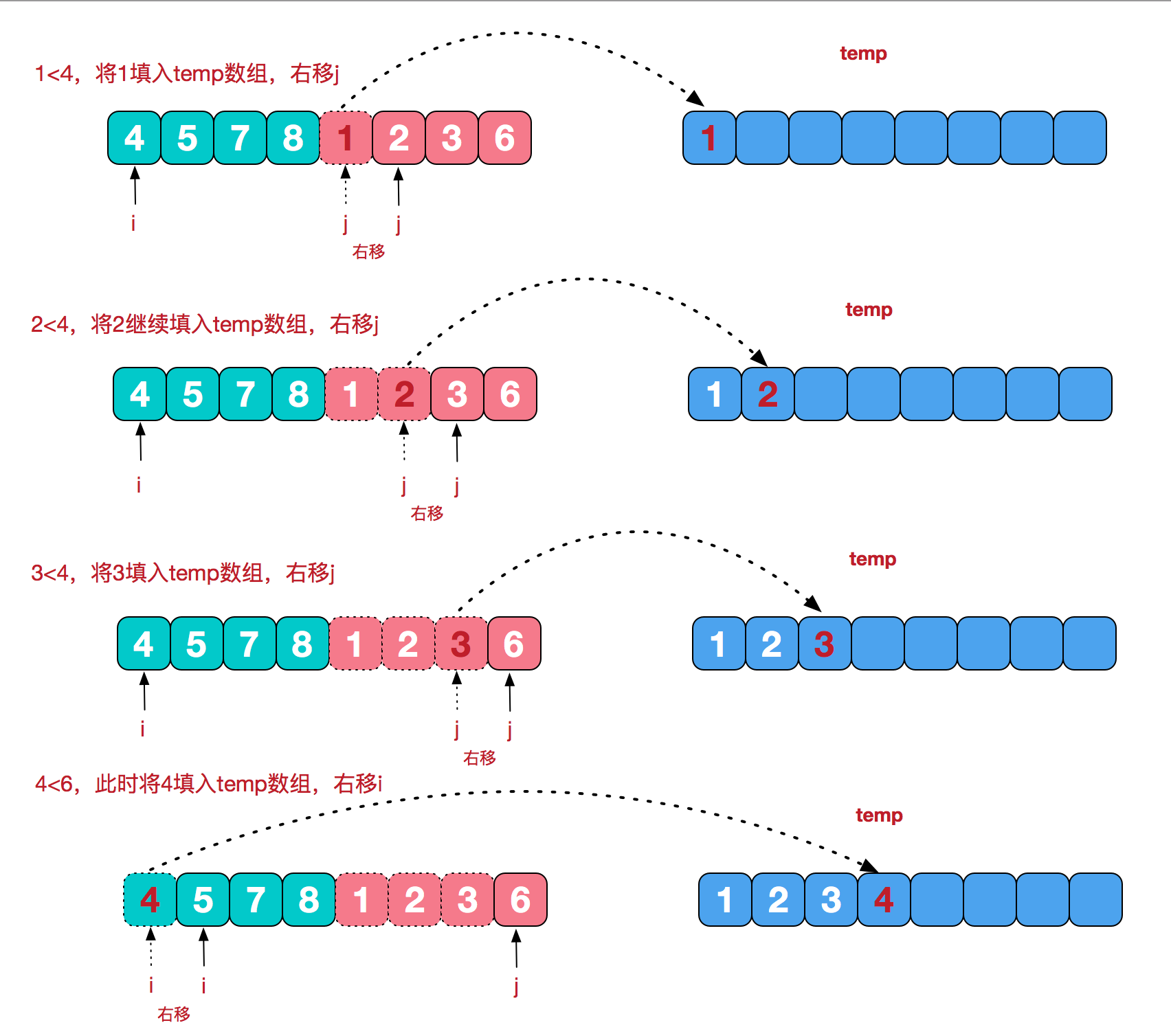
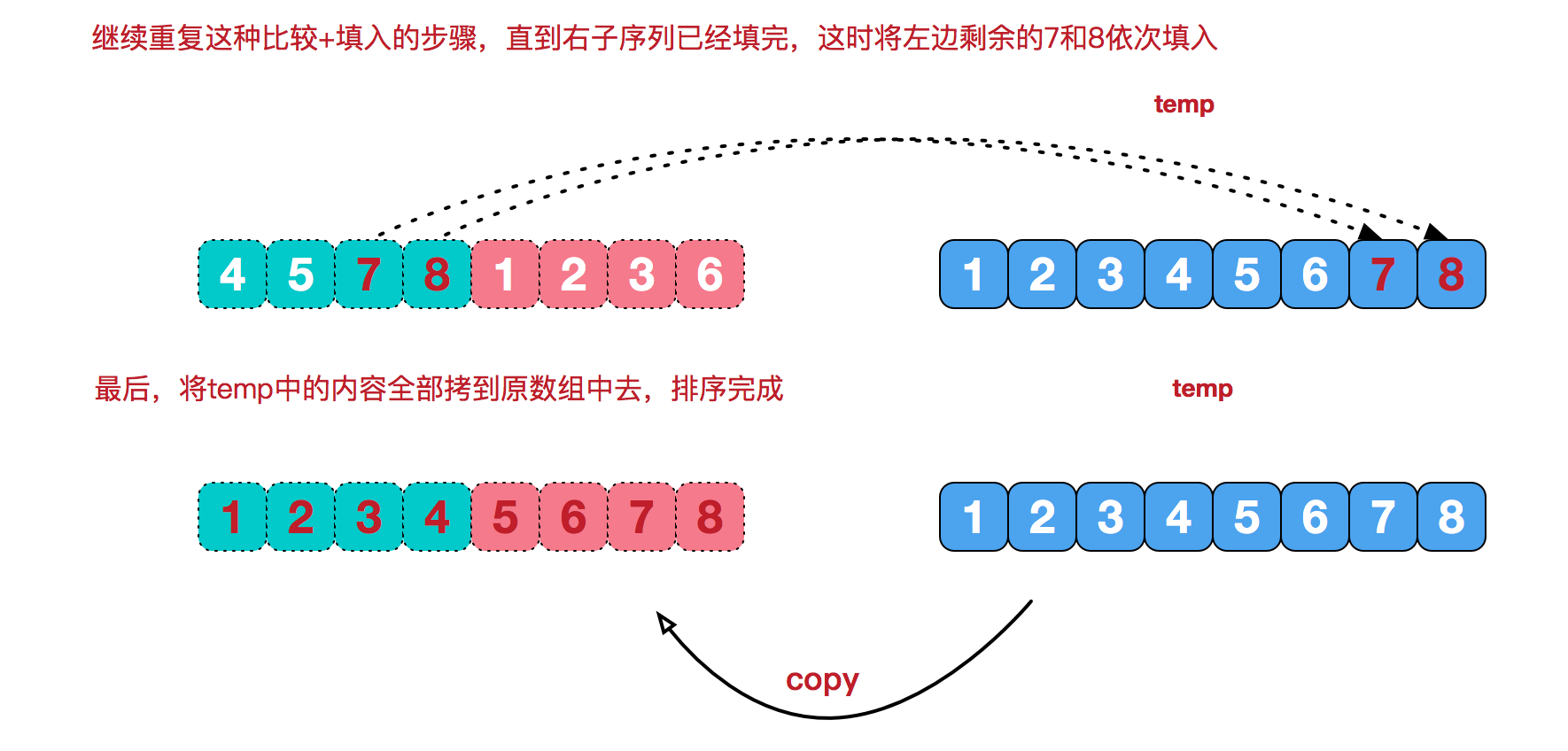
//分的过程
public static void mergeSort(int arr[],int left,int right,int []temp){
if(left<right){
int mid=(left+right)/2;
//向左递归进行分解
mergeSort(arr,left,mid,temp);
//向右递归进行分解
mergeSort(arr,mid+1,right,temp);
//到合并
merge(arr,left,mid,right,temp);
}
}
//合并的方法
/*
arr排序元素组
left左边有序序列的初始索引
mid中间索引
right右边索引
temp临时数组,作为中转
*/
public static void merge(int arr[],int left,int mid,int right,int temp[]){
int i=left;//初始化i,表示左边有序序列的初始索引
int j=mid +1;//初始化j,表示右边有序序列的初始索引
int t=0;//temp数组里面的索引,用来记录temp数组的位置
//先把左右两边(有序)的数据按照规则填充到temp数组
//直到左右两边的有序序列,有一边处理完毕为止。
while(i<=mid&&j<=right){
if(arr[i]<=arr[j]){//如果左边的小,就将左边拷贝到temp
temp[t]=arr[i];
t++;//temp数组索引后移
i++;//i后移,判断下一个跟arr[j]比
}else {//同理右边小,就将右边的拷贝到temp
temp[t]=arr[j];
t++;
j++;
}
}
//把有剩余数据的一边的数据依次全部填充到temp数组
while(i<=mid){
temp[t]=arr[i];
t++;
i++;
}
while (j<=right){
temp[t]=arr[j];
t++;
j++;
}
//将temp数组的元素拷贝到arr数组
//并不是每次都拷贝所有
t=0;
int templeft=left;//
while (templeft<=right){//第一次合并,templeft=0,right=1,第二次合并templeft=2,right=3,第三次合并temt=0,right=3
//最后一次才是拷贝全部0-7,temt=0,right=7
arr[templeft]=temp[t];
t++;
templeft++;
}
}
归并排序是先分组,后并,将两组的数据运用双索引进行比较,先将小的数据存入临时数组,当两组合并完成,就把临时数组的元素覆盖到原数组,此时原数组的两组的位置上就变成了新的一个有序的一组,然后重复该步骤,直到整个原数组成为唯一一个有序的组。
基数排序
基数排序是根据键值分组,放进不同的“桶”里面。
将所有待比较数值(自然数)统一为同样的数位长度,数位较短的数前面补零。然后,从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列。
- 先构建编号为0-9的桶(每个桶使用一维数组进行存放)
- 将每个元素的个位数取出,看这个数应该放在哪个桶上,比如52应该放在下标为2的桶,然后依次按顺序放入,桶中按照一维数组下标存储放入的数据
- 当所有数据存入桶中后,按照桶的顺序从0-9,依次取出,同一个桶的数据先从下标小的取出,将所有数据取出放入原数组
- 然后将每个元素的十位数取出,看这个数应该放在哪个桶上,比如52应该放在下标为5的桶,如果位数不够则补0,
- 然后重复第3步,就会得到一个新的序列,此时已经按照十位个位的大小进行了排序
- 如果数据还有百位就再进行一次1,2,3。同理数据最多有多少位就重复多少次1,2,3步骤,数据最多4位,则需要重复4次

public static void radixSort(int [] arr){
//定义一个二维数组,用来表示编号0-9的桶,每个桶相当于一个一维数组,为了考虑负数,所以长度加倍
//为了防止溢出,所以将每个桶的长度设置为arr的长度,相当于空间换时间
int bucket[][]=new int[20][arr.length];
//为了记录每个桶实际存放多少数据,我们定义一个数组来存放每个桶的数据,下标与桶的编号对应
int bucketCount[]=new int[20];
int max=0;//找到位数最大的那个数
String str;
int temp=0;//临时变量,记录str的长度
for(int i=0;i<arr.length;i++){//找到最大位数
str=arr[i]+"";
//如果最大位数是负数,那么String的长度还包括负号,会加一,比如-8888,String长度为5,实际上位数只有4
//所以在这里如果是负数,那么长度要减一,这样才是数字的位数,而不是数字加一个符号
temp=str.length();
if(arr[i]<0){
temp=temp-1;
}
if(temp>max){
max=temp;
}
str="";
}
int cl=1;//定义除数(arr[j]/cl)%10,第一次除1,取出个位
for(int i=0;i<max;i++){//有几位,执行几次,4位执行4次
//将arr中的数据放入桶中
for(int j=0;j<arr.length;j++){
int num=(arr[j]/cl)%10+10;//第一次循环找到个位值,第二次循环找到十位,以此类推,num+10是为了存放负数,比如-9存放在编号为1的桶,-1存放在编号为9的桶
//0存放在10号桶所以0号桶不放数据,1-9存放-9到-1,0-10存放0-9
bucket[num][bucketCount[num]]=arr[j];//根据个位值,放入到桶中
bucketCount[num]++;//计数,桶中的数据增加
}
//根据桶的顺序和桶中的下标取出数据,放入原数组
int index=0;
for(int k=0;k<bucket.length;k++){
if(bucketCount[k]!=0){//如果这个桶中有数据
for(int l=0;l<bucketCount[k];l++){
arr[index]=bucket[k][l];
bucket[k][l]=0;//将值赋值给arr后,将桶中这个位置置空
index++;//arr中每存入一个,index++
}
bucketCount[k]=0;//for循环结束,说明编号为k的桶数据全部取出,置空计数数组中下标为k的值
}
}
cl=cl*10;//为了得到数据的不同位数,第一次为1,第二次为10
//(arr[j]/cl)%10就可以循环的取出个位十位百位等
}
}