一、0-1背包问题
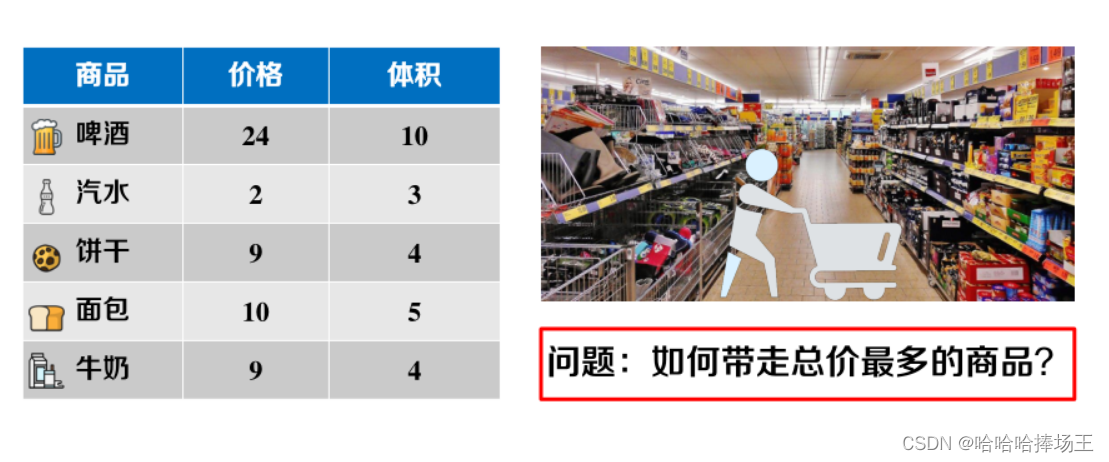
- 问题背景:超市允许顾客使用一个体积大小位13的背包,选择一件或多件商品带走,问:如何带走总价最多的商品?
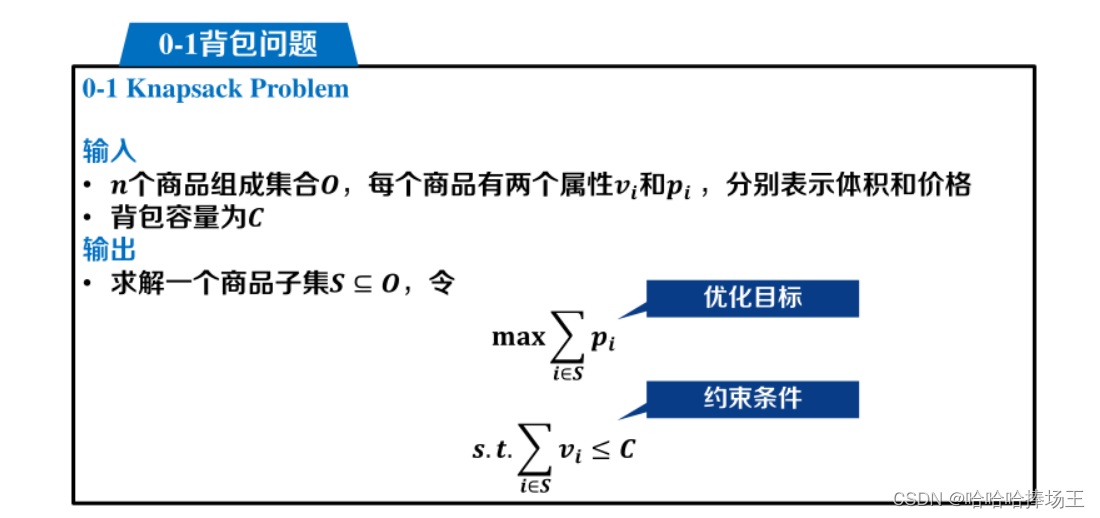
 - 形式化定义:
 - 如果我们没有学过算法设计的话,我们可能会有一些直观的选择策略,它们的核心思想为:将商品排序,依次挑选
- 策略1:按商品价格由高到低排序,优选挑选价格高的商品
- 策略2:按商品体积由小到大排序,优选挑选体积小的商品
- 策略3:按商品价值与体积的比由高到低排序,优先挑选比值高的商品
- 以上这些方法都不一定能保证我们得到最优解,为了确保我们得到最优解,我们不难想出,我们可以暴力枚举出所有商品的组合,然后我们去除不满足体积约束的解,最终我们选择最优解的集合即可。
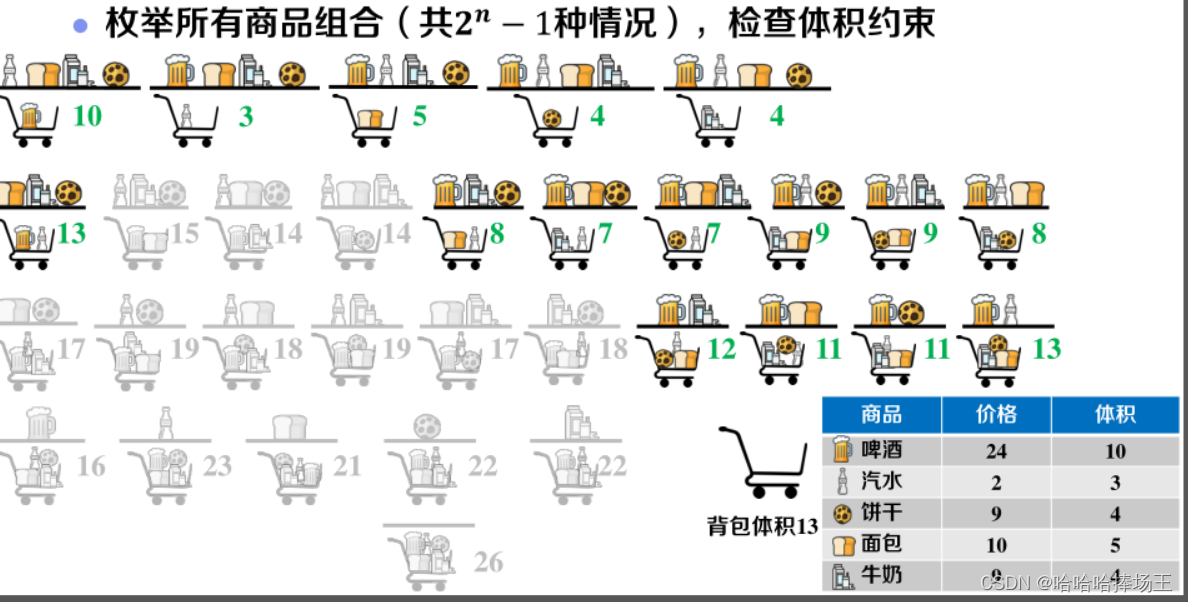
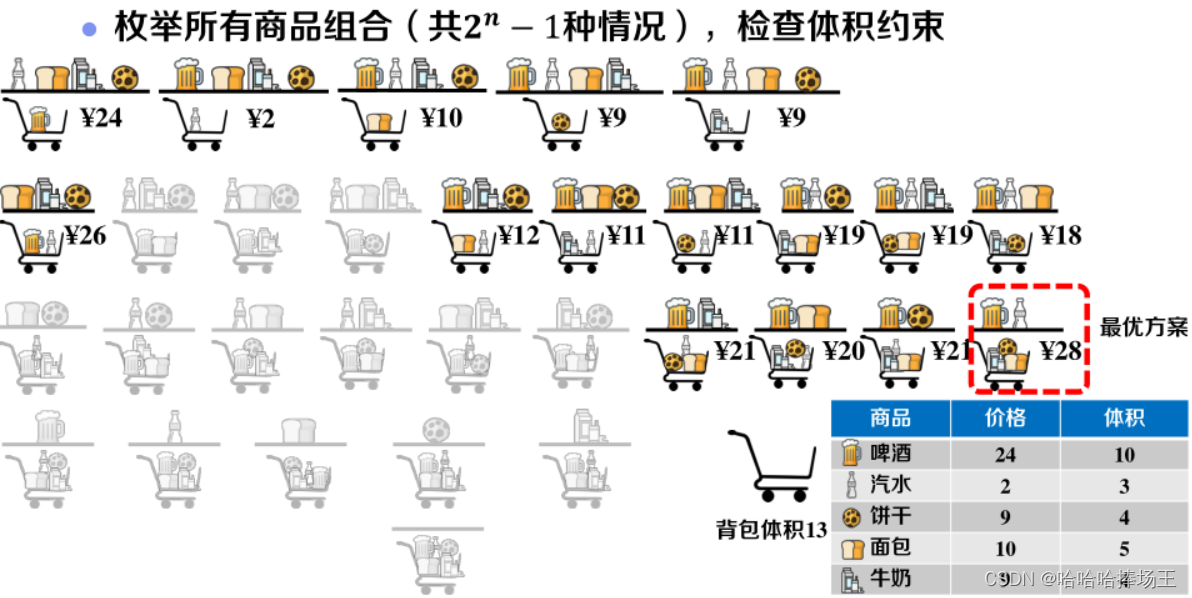 - 暴力求解过程及伪代码
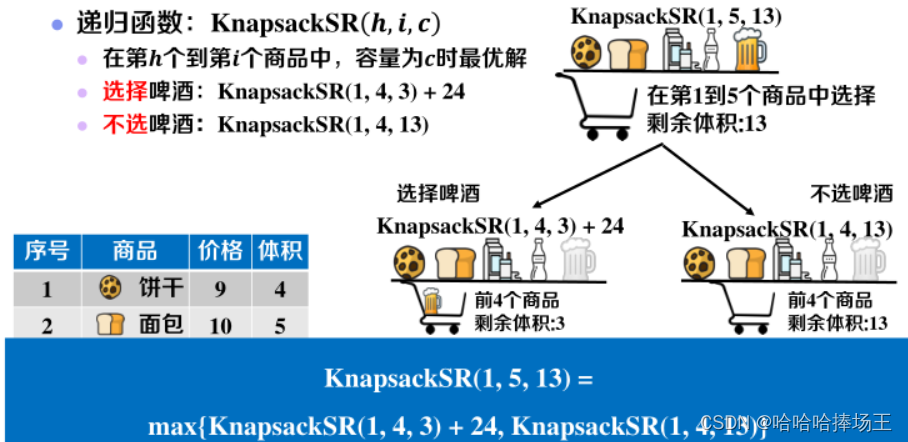
 - 优化:在上面暴力求解过程中,我们发现有许多步的计算重复了,于是我们我们想可不可以省去重复的计算?可不可以构造一个备忘录记录每个步骤的最大值,如果计算过了就直接返回最大值。

- 带备忘录的计算顺序
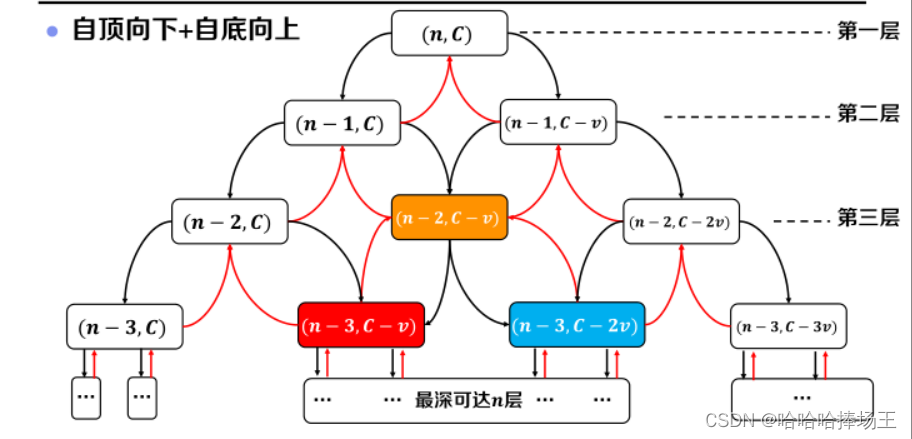
- 我们又开始想,每次都是自顶向下分解问题,但是我们可不可以直接自底向上去做,这样可以省去自顶向上的分解步骤,进一步提高算法效率。
- 递推计算:首先确定计算顺序,按照从左到右,从上到下的顺序计算
- 递推公式:
p
[
i
,
c
]
=
m
a
x
{
P
[
i
?
1
,
c
?
v
[
i
]
]
+
p
[
i
]
,
p
[
i
?
1
,
c
]
}
p[i,c]=max\{P[i -1, c-v[i]] + p[i], p[i-1,c] \}
p[i,c]=max{P[i?1,c?v[i]]+p[i],p[i?1,c]}
 - 伪代码

- 上面三种方法的代码实现
package com.tiger.study;
import java.util.ArrayList;
import java.util.HashMap;
public class BagProblem {
public static void main(String[] args) {
int[][] priceAndV = {{24, 10}, {2, 3}, {9, 4}, {10, 5}, {9, 4}};
int c = 13;
int[][] mem = new int[priceAndV.length + 1][c + 1];
boolean[][] records = new boolean[priceAndV.length + 1][c + 1];
for (int i1 = 0; i1 < mem.length; i1++) {
mem[i1][0] = 0;
records[i1][0] = false;
}
for (int i1 = 0; i1 < mem[0].length; i1++) {
mem[0][i1] = 0;
records[0][i1] = false;
}
HashMap<String, Integer> map = new HashMap<>();
KnapsackDP(priceAndV, priceAndV.length, c, mem, records);
System.out.println(mem[priceAndV.length][c]);
ArrayList<Integer> commoditys = new ArrayList<>();
int nums = priceAndV.length;
while (nums >= 0 && c >= 0) {
if (records[nums][c]) {
commoditys.add(nums);
c -= priceAndV[nums - 1][1];
nums--;
} else {
nums--;
}
}
System.out.println(commoditys);
for (int i = 0; i < mem.length; i++) {
for (int i1 = 0; i1 < mem[i].length; i1++) {
System.out.printf(mem[i][i1] + " ");
}
System.out.println();
}
}
private static int KnapsackSREnum(int[][] arr, int i, int c) {
if (c < 0) return -Integer.MAX_VALUE;
if (0 >= i) return 0;
int v = arr[i][1];
int p = arr[i][0];
int p1 = KnapsackSREnum(arr, i - 1, c - v);
int p2 = KnapsackSREnum(arr, i - 1, c);
int maxP = Math.max(p1 + p, p2);
return maxP;
}
private static int KnapsackSREnum(int[][] arr, int i , int c, HashMap<String, Integer> map) {
if (c < 0) return -Integer.MAX_VALUE;
if (0 >= i) return 0;
if (map.containsKey(i + "," + c)) return map.get(i + "," + c);
int p = arr[i][0];
int v = arr[i][1];
int p1 = KnapsackSREnum(arr, i - 1, c - v, map);
int p2 = KnapsackSREnum(arr, i - 1, c, map);
int pMax = Math.max(p1 + p, p2);
map.put(i + "," + c, pMax);
return map.get(i + "," + c);
}
private static int KnapsackSREnum(int[][] arr, int i, int c, int[][] memorandums) {
if (c < 0) return -Integer.MAX_VALUE;
if (i <= 0) return 0;
int p = arr[i][0];
int v = arr[i][1];
int p1 = KnapsackSREnum(arr, i - 1, c, memorandums);
int p2= KnapsackSREnum(arr, i - 1, c - v, memorandums) + p;
if (p1 > p2) {
memorandums[i][c] = p1;
} else {
memorandums[i][c] = p2;
}
return memorandums[i][c];
}
private static int KnapsackSREnum(int[][] arr, int i, int c, int[][] memorandums, boolean[][] records) {
if (c < 0) return -Integer.MAX_VALUE;
if (i <= 0) return 0;
int p = arr[i][0];
int v = arr[i][1];
int p1 = KnapsackSREnum(arr, i - 1, c, memorandums, records);
int p2= KnapsackSREnum(arr, i - 1, c - v, memorandums, records) + p;
if (p1 < p2 && v <= c) {
memorandums[i + 1][c] = p2;
records[i + 1][c] = true;
} else {
memorandums[i + 1][c] = p1;
records[i + 1][c] = false;
}
return memorandums[i + 1][c];
}
private static void KnapsackDP(int[][] arr, int i, int c, int[][] memorandums, boolean[][] records) {
for (int i1 = 1; i1 <= i; i1++) {
for (int i2 = 1; i2 <= c; i2++) {
int v = arr[i1 - 1][1];
int p_i = arr[i1 - 1][0];
if (i2 < v) {
memorandums[i1][i2] = 0;
records[i1][i2] = false;
continue;
}
int p_1= memorandums[i1 - 1][i2 - v] + p_i;
int p_2 = memorandums[i1 - 1][i2];
if (p_1 >= p_2 && v <= i2) {
memorandums[i1][i2] = p_1;
records[i1][i2] = true;
} else {
memorandums[i1][i2] = p_2;
records[i1][i2] = false;
}
}
}
}
}
二、动态规划
- 从上面背包问题引出动态规划,在背包问题中我们提出了三种解决方案,后两种方案被成为动态规划
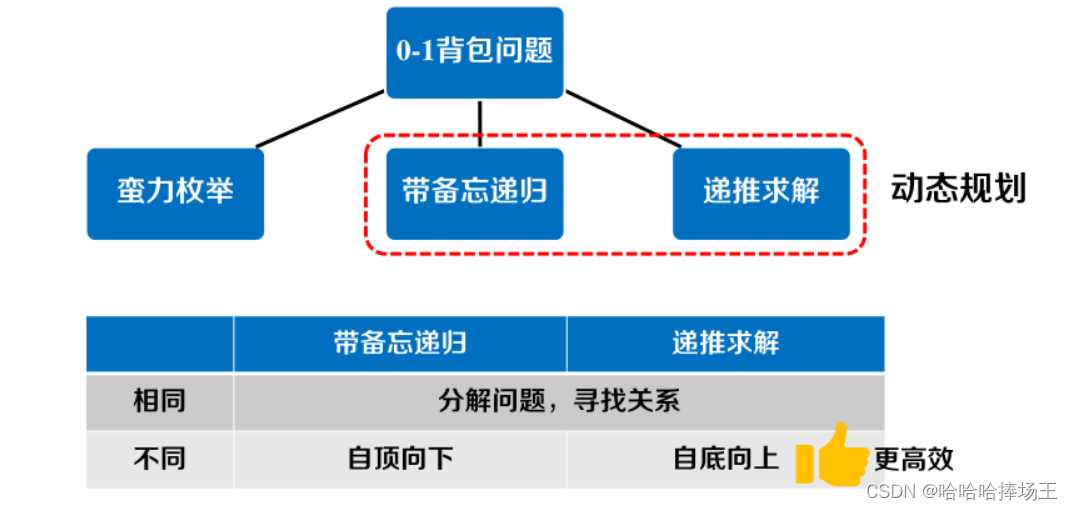 - 动态规划的一般步骤:
- 问题结构分析
- 递推关系建立
- 分析最优(子)结构。最优子结构的性质:问题的最优解由相关问题最优解组合而成,并且子问题可以独立求解
- 自底向上计算
- 最优方案追踪
- 动态规划小结
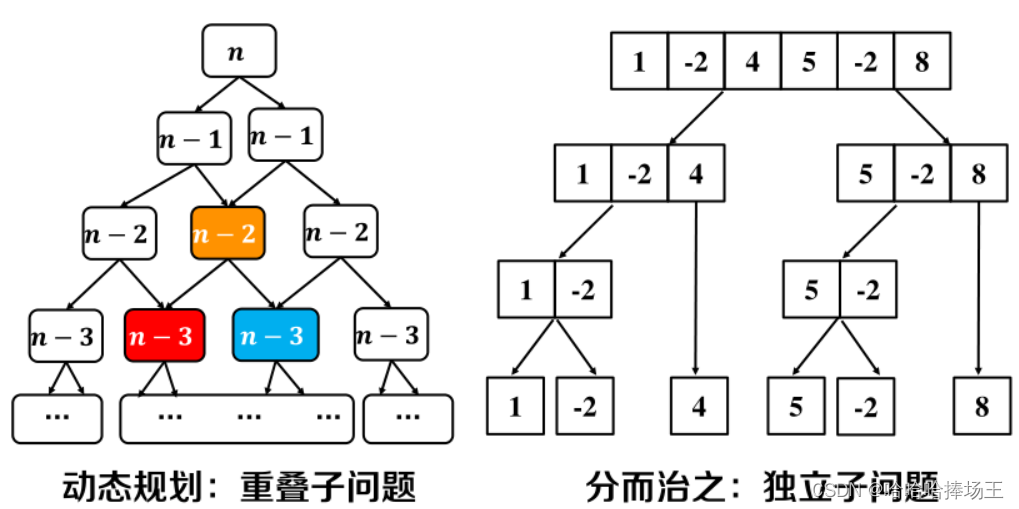
- 动态规划与分而治之的区别
 - 如何设计一个动态规划算法?四个步骤

三、最大子数组问题
- 在前面我们使用分治算法求解过这个问题,在哪里我们先将数组划分为小数组,然后计算每个小数组的最大子数组,在计算跨中间的。这里我们使用动态规划来求解。
private static int[] maxSubArrayDP(int[] arr) {
int[] results = new int[arr.length];
int[] records = new int[arr.length];
int j = arr.length - 1;
while (j >= 0) {
if (j == arr.length - 1) {
results[j] = arr[j];
records[j] = j;
j--;
} else {
if (results[j + 1] > 0) {
results[j] = arr[j] + results[j + 1];
records[j] = records[j + 1];
j--;
} else {
results[j] = arr[j];
records[j] = j;
j--;
}
}
}
int max = Integer.MIN_VALUE;
int max_index = 0;
for (int i = 0; i < results.length; i++) {
if (results[i] > max) {
max = results[i];
max_index = i;
}
}
int[] maxSub = new int[records[max_index] - max_index + 1];
for (int i = max_index; i <= records[max_index]; i++) {
maxSub[i - max_index] = arr[i];
}
return maxSub;
}
四、最长公共子序列问题
- 问题描述:求两个序列中的最长公共子序列,子序列可能不唯一
package com.tiger.study;
public class LongestCommonSubsequenceProblem {
public static void main(String[] args) {
char[] x = {'A', 'B', 'C', 'B', 'D', 'A', 'B'};
char[] y = {'B', 'D', 'C', 'A', 'B', 'A'};
int[][] memor = new int[x.length + 1][y.length + 1];
String[][] record = new String[x.length][y.length];
for (int i = 0; i < x.length; i++) {
memor[i][0] = 0;
}
for (int i = 0; i < y.length; i++) {
memor[0][i] = 0;
}
longestCommSubseq(x, y, memor, record);
System.out.println(memor[x.length][y.length]);
int x_head = x.length - 1;
int y_head = y.length - 1;
int longestCommLen = memor[x.length][y.length];
char[] longestComm = new char[longestCommLen];
longestCommLen--;
while (longestCommLen >=0) {
if (record[x_head][y_head] == "L") {
y_head -= 1;
longestComm[longestCommLen] = y[y_head];
longestCommLen--;
} else if (record[x_head][y_head] == "U") {
x_head -= 1;
longestComm[longestCommLen] = x[x_head];
longestCommLen--;
} else {
x_head -= 1;
y_head -= 1;
longestComm[longestCommLen] = x[x_head];
longestCommLen--;
}
}
for (int i = 0; i < longestComm.length; i++) {
System.out.println(longestComm[i] + " ");
}
for (int i = 0; i < record.length; i++) {
for (int j = 0; j < record[i].length; j++) {
System.out.printf(record[i][j] + " ");
}
System.out.println();
}
for (int i = 0; i < memor.length; i++) {
for (int j = 0; j < memor[i].length; j++) {
System.out.printf(memor[i][j] + " ");
}
System.out.println();
}
}
private static void longestCommSubseq(char[] x, char[] y, int[][] memor, String[][] records) {
for (int i = 0; i < x.length; i++) {
for (int j = 0; j < y.length; j++) {
if (x[i] == y[j]) {
memor[i + 1][j + 1] = memor[i][j] + 1;
records[i][j] = "LU";
} else {
if (memor[i][j + 1] >= memor[i + 1][j]) {
memor[i + 1][j + 1] = memor[i][j + 1];
records[i][j] = "U";
} else {
memor[i + 1][j + 1] = memor[i + 1][j];
records[i][j] = "L";
}
}
}
}
}
}
五、最长子串问题
- 问题描述:给定两个序列,求这两个序列中最长的公共子串
package com.tiger.study;
public class LongestCommomSubstringProblem {
public static void main(String[] args) {
char[] x = {'A', 'B', 'C', 'A', 'D', 'B', 'B'};
char[] y = {'B', 'C', 'E', 'D', 'B', 'B'};
char[] substr = longestCommSubstr(x, y);
for (int i = 0; i < substr.length; i++) {
System.out.println(substr[i]);
}
}
private static char[] longestCommSubstr(char[] x, char[] y) {
int[][] mem = new int[x.length + 1][y.length + 1];
int pMaxIndex = 0;
int pLen = 0;
for (int i = 0; i < mem.length; i++) {
mem[i][0] = 0;
}
for (int i = 0; i < mem[0].length; i++) {
mem[0][i] = 0;
}
for (int i = 0; i < x.length; i++) {
for (int j = 0; j < y.length; j++) {
if (x[i] == y[j]) {
mem[i + 1][j + 1] = mem[i][j] + 1;
if (mem[i + 1][j + 1] > pLen) {
pMaxIndex = i;
pLen = mem[i + 1][j + 1];
}
} else {
mem[i + 1][j + 1] = 0;
}
}
}
char[] res = new char[pLen];
for (int i = pLen; i > 0; i--) {
res[pLen - i] = x[pMaxIndex - i + 1];
}
return res;
}
}
六、编辑距离问题
- 问题描述:给定两个字符串,有三种操作:删除,插入,替换,问字符串1最少需要操作几次才能转换为字符串2?
package com.tiger.study;
public class EditDistanceProblem {
public static void main(String[] args) {
String word1 = "abcbdab";
String word2 = "bdcaba";
System.out.println(editDistance(word1, word2));
}
private static int editDistance(String word1, String word2) {
char[] x1 = word1.toCharArray();
char[] x2 = word2.toCharArray();
int[][] mem = new int[x1.length + 1][x2.length + 1];
for (int i = 0; i < mem.length; i++) {
mem[i][0] = i;
}
for (int i = 0; i < mem[0].length; i++) {
mem[0][i] = i;
}
for (int i = 0; i < x1.length; i++) {
for (int j = 0; j < x2.length; j++) {
int flag = 1;
if (x1[i] == x2[j]) {
flag = 0;
}
mem[i + 1][j + 1] = Math.min(Math.min(mem[i][j + 1] + 1, mem[i + 1][j] + 1), mem[i][j] + flag);
}
}
return mem[x1.length][x2.length];
}
}
|












