[数据结构与算法]java七大排序算法你学废了吗

排序的定义

概念

排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。
平时的上下文中，如果提到排序，通常指的是排升序（非降序）。
通常意义上的排序，都是指的原地排序(in place sort)

稳定性

两个相等的数据，如果经过排序后，排序算法能保证其相对位置不发生变化，则我们称该算法是具备稳定性的排序算法。

七大排序

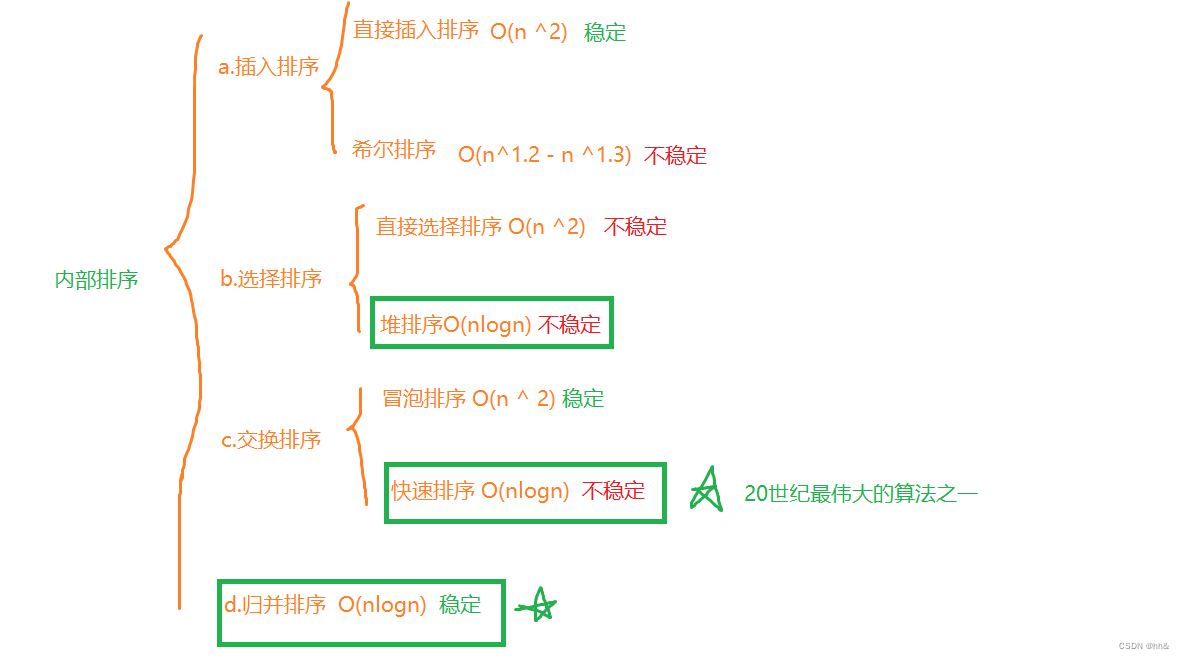
冒泡排序

/**
     * 冒泡排序
     *
     * @param arr
     */
    public static void bubbleSort(int[] arr) {
        for (int i = 0; i < arr.length - 1; i++) {
            boolean isSwap = false;
            for (int j = 0; j < arr.length - i - 1; j++) {
                if (arr[j] > arr[j + 1]) {
                    swap(arr, j, j + 1);
                    isSwap = true;
                }
            }
            if (!isSwap) {
                //内层没有元素交换
                break;
            }
        }
    }

选择排序

时间复杂度:O(n^2)

选择排序是一个不稳定的排序算法

下面的例子中5a就会被交换到前面去.

每一次从无序区间选出最大（或最小）的一个元素，存放在无序区间的最后（或最前),直到全部待排序的数据元素排完

public static void selectionSort(int[] arr) {
        //外层循环,要找几次,比如11个数,只需要找10次,最后一个数不用比
        for (int i = 0; i < arr.length - 1; i++) {
            //min是未排序元素的第一个
            int min = i;
            //每次找出最小的数
            for (int j = i + 1; j < arr.length; j++) {
                if (arr[j] < arr[min]) {
                    min = j;
                }
            }
            //min对应的一定是数组中的最小值的索引
            //将最小值和待排序的第一个元素交换
            //已排序元素+1
            swap(arr, i, min);
        }
    }

双向选择排序

 public static void doubleSelectionSort(int[] arr) {
        int left = 0;
        int right = arr.length - 1;
        while (left <= right) {
            int min = left;
            int max = right;
            for (int i = left + 1; i <= right; i++) {
                if (arr[i] < arr[min]) {
                    min = i;
                }
                if (arr[i] > arr[max]) {
                    max = i;
                }
            }
            swap(arr, min, left);
            if (max == left) {
                max = min;
            }
            swap(arr, max, right);
            left++;
            right--;
        }
    }

插入排序

每次从无序区间选择一个数,插入到有序区间的合适位置,默认第一个数就是有序的.

public static void insertSort(int[] arr) {
        for (int i = 1; i < arr.length; i++) {
            for (int j = i; j > 0; j--) {
                if (arr[j] > arr[j - 1]) {
                    break;
                } else {
                    swap(arr, j, j - 1);
                }
            }
        }
    }

二分插入排序

public static void insertSortBS(int[] arr) {
        // 已排序区间 [0,i)
        // 未排序区间 [i,arr.length)
        for (int i = 1; i < arr.length; i++) {
            int val = arr[i];
            int left = 0;
            int right = i;
            while (left < right) {
                int mid = (left + right) >> 1;
                if (arr[i] > arr[mid]) {
                    left = mid + 1;
                } else {
                    // 这块是right = mid,如果right = mid - 1 
                    // [4,15,8] 这种情况下就会出错
                    right = mid;
                }
            }
            // 将这个数插入到left的位置,搬移left之后的元素
            for (int j = i; j > left; j--) {
                arr[j] = arr[j - 1];
            }
            // 将这个数插入到left的位置
            arr[left] = val;
        }
    }

希尔排序

希尔排序法又称为缩小增量排序法,是对插入排序的优化

时间复杂度:O(n)=n^1.2~n^1.3(了解即可)

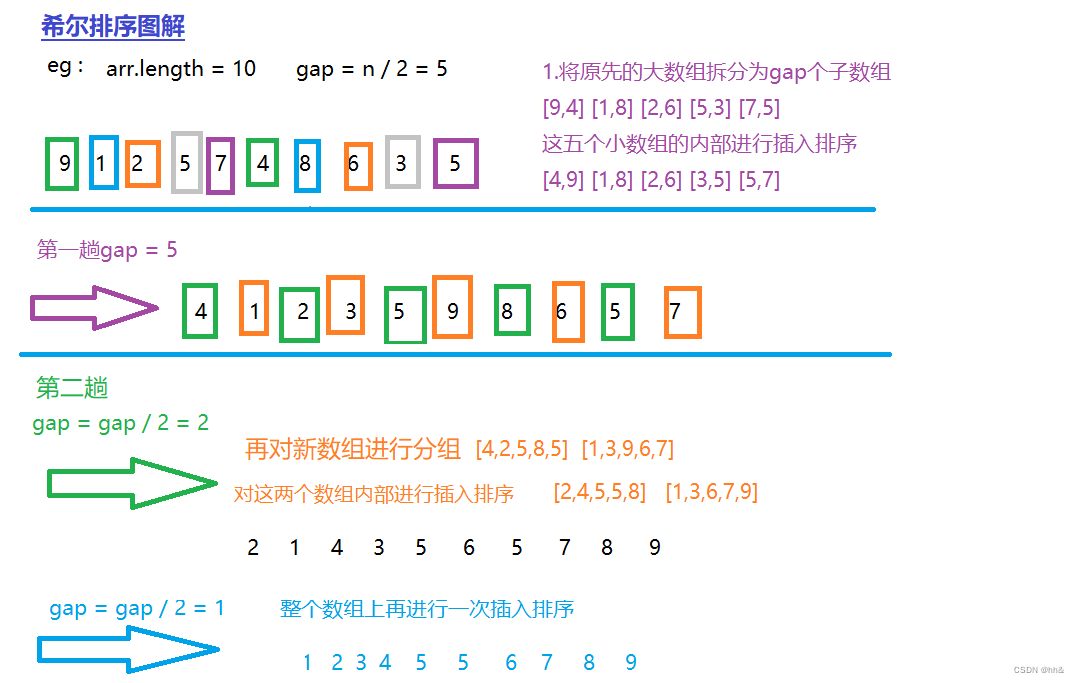
希尔排序的基本思想是:选取一个整数gap,将待排序的数组分成相同的小数组,所有距离相同的元素分在同一组内,然后对每个小数组进行排序,然后重复上述过程,直到gap等于1,所有数据在一组内排好序.

我们发现:当小数组被调整的近乎有序后,再组合成大数组,此时的大数组也近乎有序的状态,此时,插入排序的效率将非常高.

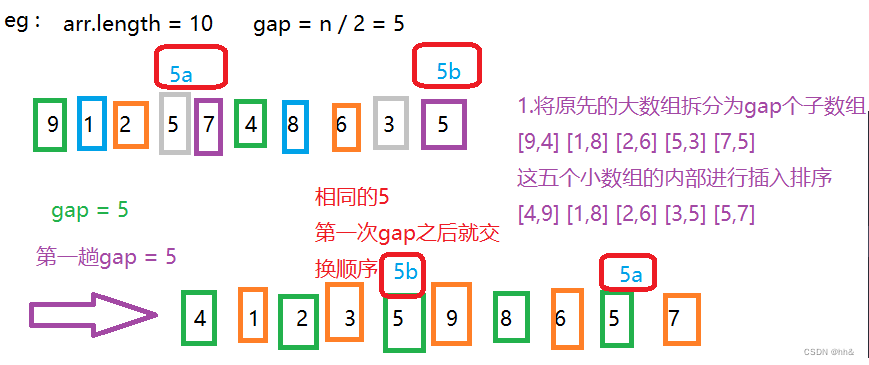
希尔排序是一个不稳定的排序算法,因为,在排序过程中有可能相同的两个值被分到不同的子数组,有可能交换他们的顺序.

    /**
     * 希尔排序
     * 缩小增量排序,将原数组按照gap分成gap个子数组,将子数组进行内部插入排序,不断缩小gap,直到gap==1
     * 此时数组已近乎接近有序,只需要最后进行一次插入排序即可.
     *
     * @param arr
     */
    public static void shellSort(int[] arr) {
        int gap = arr.length >> 1;

        //预处理
        while (gap > 1) {
            insertionSortByGar(arr, gap);
            gap = gap >> 1;
        }
        //此时gar等于1,数组近乎有序,进行最后一次插入排序
        insertionSortByGar(arr,gap);
    }

    //内部排序
    private static void insertionSortByGar(int[] arr, int gap) {
        for (int i = gap; i < arr.length; i++) {
            for (int j = i; j - gap >= 0; j = j - gap) {
                if (arr[j] < arr[j - gap]) {
                    swap(arr, j, j - gap);
                } 
            }
        }
    }

总结:希尔排序的核心是将一个大数组,分为gap个小数组,然后将小数组里面的元素排好序(插入排序),然后gap=gap/2,继续上述过程,直到gap= 1,变为了一个数组,此时元素接近有序,使用插入排序的效率将会非常高,插入排序算法对接近有序的小数组的排序处理非常高效.

归并排序

归:不断将原数组拆分为子数组(一分为二),直到子数组只剩下一个元素,拆分结束.
并:不断合并两个相邻的子数组为一个大的有序子数组,合并过程就是将已经有序的子数组合并为一个更大的有序子数组,直到合并整个数组结束.

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-3hJ8j8F8-1661710014743)(java七大排序算法,你学废了吗.assets/图片-18.jpg)]

/**
     * 归并排序递归写法
     *
     * @param arr
     */
    public static void mergeSort(int[] arr) {
        mergeSortInternal(arr, 0, arr.length - 1);
    }

    private static void mergeSortInternal(int[] arr, int l, int r) {
        // 1. 归并的归过程
        if (l >= r) {
            return;
        }
        // 注意这块一定要带括号
        int mid = l + ((r - l) >> 1);
        mergeSortInternal(arr, l, mid);
        mergeSortInternal(arr, mid + 1, r);
        // 2.归并的并过程
        merge(arr, l, r, mid);
    }

    private static void merge(int[] arr, int l, int r, int mid) {
        // 先创建一个临时数组
        // l = 0 , r = 1   1- 0 + 1 == 2
        // 创建一个临时数组
        int[] aux = new int[r - l + 1];
        // 将原数组的值复制到临时数组
        for (int i = 0; i < aux.length; i++) {
            // 注意偏移量
            aux[i] = arr[i + l];
        }

        // 第一个数组起始位置
        int i = l;
        // 第二个数组起始位置
        int j = mid + 1;
        for (int k = l; k <= r; k++) {
            if (i > mid) {
                // 数组1遍历完毕
                arr[k] = aux[j - l];
                j++;
            } else if (j > r) {
                // 数组2遍历完毕
                arr[k] = aux[i - l];
                i++;
            } else if (aux[i - l] < aux[j - l]) {
                arr[k] = aux[i - l];
                i++;
            } else {
                arr[k] = aux[j - l];
                j++;
            }
        }
    }

快速排序

从无序区间选择一个值pivot,开始扫描原集合,将数组中所有小于该pivot的值放在分界点的左侧,所有大于pivot的值放在分界点的右侧,经过本轮交换,pivot放在了最终的位置,左侧是小于pivot的元素,右侧是大于pivot的元素,重复上述过程,直到整个数组有序为止.

分区方法有两种(核心就是分区)

Hoare法

 /**
     * Hoare
     * 本质和挖坑法相同,不过挖坑法是直接赋值,它是交换
     * @param arr
     */
    public static void quickSort(int[] arr) {
        quickSortInternal(arr, 0, arr.length - 1);
    }

    private static void quickSortInternal(int[] arr, int left, int right) {
        if (left >= right) {
            return;
        }
        int p = partition(arr, left, right);
        quickSortInternal(arr, left, p - 1);
        quickSortInternal(arr, p + 1, right);
    }

    private static int partition(int[] arr, int left, int right) {
        int i = left;
        int j = right;
        int tmp = arr[left];
        while (i < j) {
            while (i < j && arr[j] >= tmp) {
                j--;
            }
            // arr[j] < tmp
            while (i < j && arr[i] <= tmp) {
                i++;
            }
            // arr[i] > tmp
            swap(arr, i, j);
        }
        // i多指向的是最后一个小于tmp的数
        swap(arr, left, i);
        return i;
    }

    private static void swap(int[] arr, int left, int right) {
        int temp = arr[left];
        arr[left] = arr[right];
        arr[right] = temp;
    }

挖坑分区法

时间复杂度分析

稳定性:不稳定

最好:O(N*logN)

最坏:有序或者逆序,就会退化为一棵单分支的树,此时时间复杂度应该为O(N^2)

空间复杂度分析

最好:O(logN) 递归要保存数据,所以就是树的高度

最坏:O(n) 退化称为一个单分支的树,递归次数为n次.

如果是接近有序的数组,那么快排的时间复杂度为o(^N),空间复杂度为O(n),递归次数太多,会将栈挤爆.

public static void quickSort(int[] arr) {
        quickSortInternal(arr, 0, arr.length - 1);
    }

    private static void quickSortInternal(int[] arr, int start, int end) {
        if (start >= end) {
            return;
        }
        int p = paration(arr, start, end);
        quickSortInternal(arr, start, p - 1);
        quickSortInternal(arr, p + 1, end);
    }

    private static int paration(int[] arr, int start, int end) {
        int tmp = arr[start];
        while (start < end) {
            // 要加=,不然就会死循环
            while (start < end && arr[end] >= tmp) {
                end--;
            }
            // end走到了小于temp 的地方
            arr[start] = arr[end];
            // 也加上
            while (start < end && arr[start] <= tmp) {
                start++;
            }
            // start走到了大于tmp的地方
            arr[end] = arr[start];
        }
        arr[start] = tmp;
        return start;
    }

前后遍历法

/**
 * 前后遍历法
 *
 * @param arr
 */
public static void quickSort(int[] arr) {
    quickSortInternal(arr, 0, arr.length - 1);
}

private static void quickSortInternal(int[] arr, int left, int right) {
    if (left >= right) {
        return;
    }
    int p = partition(arr, left, right);
    quickSortInternal(arr, left, p - 1);
    quickSortInternal(arr, p + 1, right);
}

private static int partition(int[] arr, int left, int right) {
    int i = left;
    int j = i + 1;
    int tmp = arr[left];
    while (j <= right) {
        if (arr[j] < tmp) {
            swap(arr, i + 1, j);
            i++;
        }
        j++;
    }
    swap(arr, i, left);
    return i;
}

private static void swap(int[] arr, int left, int right) {
    int temp = arr[left];
    arr[left] = arr[right];
    arr[right] = temp;
}

快速排序优化

1. 随机取基准

2. 三数取中

3. 将和基准相同的值移动跟前

4. 区间小的时候,采用插入排序

 /**
     * 挖坑法 优化,使用三数取中法
     */
    public static void quickSort(int[] arr) {
        quickSortInternal(arr, 0, arr.length - 1);
    }

    private static void quickSortInternal(int[] arr, int left, int right) {
        if (left >= right) {
            return;
        }

        // 优化2
        if ((right - left + 1) < 40) {
            // 使用插入排序
            // TODO
            return;
        }

        // 优化1
        // 找基准之前,我们先找到中间值
        int midIndex = finMidValueIndex(arr, left, right);
        swap(arr, left, midIndex);

        int p = partition(arr, left, right);
        quickSortInternal(arr, left, p - 1);
        quickSortInternal(arr, p + 1, right);
    }

    /**
     * 防止堆栈溢出,三数取中法
     *
     * @param arr
     * @param start
     * @param end
     * @return
     */
    private static int finMidValueIndex(int[] arr, int start, int end) {
        int mid = start + ((end - start) >>> 1);
        if (arr[start] < arr[end]) {
            if (arr[mid] < arr[start]) {
                return start;
            } else if (arr[mid] > arr[end]) {
                return end;
            } else {
                return mid;
            }
        } else {
            if (arr[mid] > start) {
                return start;
            } else if (arr[mid] < arr[end]) {
                return end;
            } else {
                return mid;
            }
        }
    }

    private static int partition(int[] arr, int left, int right) {
        int tmp = arr[left];

        while (left < right) {
            while (left < right && arr[right] >= tmp) {
                right--;
            }
            // right走到了小于temp 的地方
            arr[left] = arr[right];
            while (left < right && arr[left] < tmp) {
                left++;
            }
            // left走到了大于tmp的地方
            arr[right] = arr[left];
        }
        arr[left] = tmp;
        return left;
    }

    private static void swap(int[] arr, int left, int right) {
        int temp = arr[left];
        arr[left] = arr[right];
        arr[right] = temp;
    }

堆排序

/**
     * 堆排序
     *
     * @param arr
     */
    public static void heapSort(int[] arr) {
        // 先堆化调整为最大堆
        for (int i = parent(arr.length - 1); i >= 0; i--) {
            siftDown(arr, i, arr.length);
        }
        // 不断的将堆顶元素(最大值)和最后的元素交换,然后再将堆顶元素下沉
        // 这样每次都能将一个最大值放到正确位置
        // 时间复杂度为 nlogN
        for (int i = arr.length - 1; i > 0; i--) {
            swap(arr, 0, i);
            // 这块应该注意已经放好的元素,不应该在参与到siftdown操作了,所以边界是i
            siftDown(arr, 0, i);
        }
    }

    private static void siftDown(int[] arr, int i, int length) {
        while (leftChild(i) < length) {
            // 还有左子树
            int j = leftChild(i);
            if (j + 1 < length && arr[j] < arr[j + 1]) {
                // 右边 > 左边
                ++j;
            }
            // j对应的最大值必须得加,如果不加,就会形成死循环
            // 因为if判断进不去,那样的话 i 的值就没法改变,所以就会产生循环
            // else
            if (arr[i] < arr[j]) {
                swap(arr, i, j);
                i = j;
            } else {
                break;
            }
        }
    }

    private static void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }

    private static int leftChild(int i) {
        return 2 * i + 1;
    }

    private static int parent(int i) {
        return (i - 1) >> 1;
    }

堆排序和快速排序的区别

虽然它们的时间复杂度都是O(NlogN),但是不管在什么情况下,堆排序都是O(NlogN),而快排在有序的情况下,会退化为O(N^2)