BFS使用场景
- 连通块问题:(通过一个点找到图中连通的所有点)
- 分层遍历:(图的层次遍历、简单图的最短路径)
- 拓扑排序:(求任意拓扑排序、求是否有拓扑排序、求字典序最小的拓扑序、求是否唯一拓扑序)
树的BFS
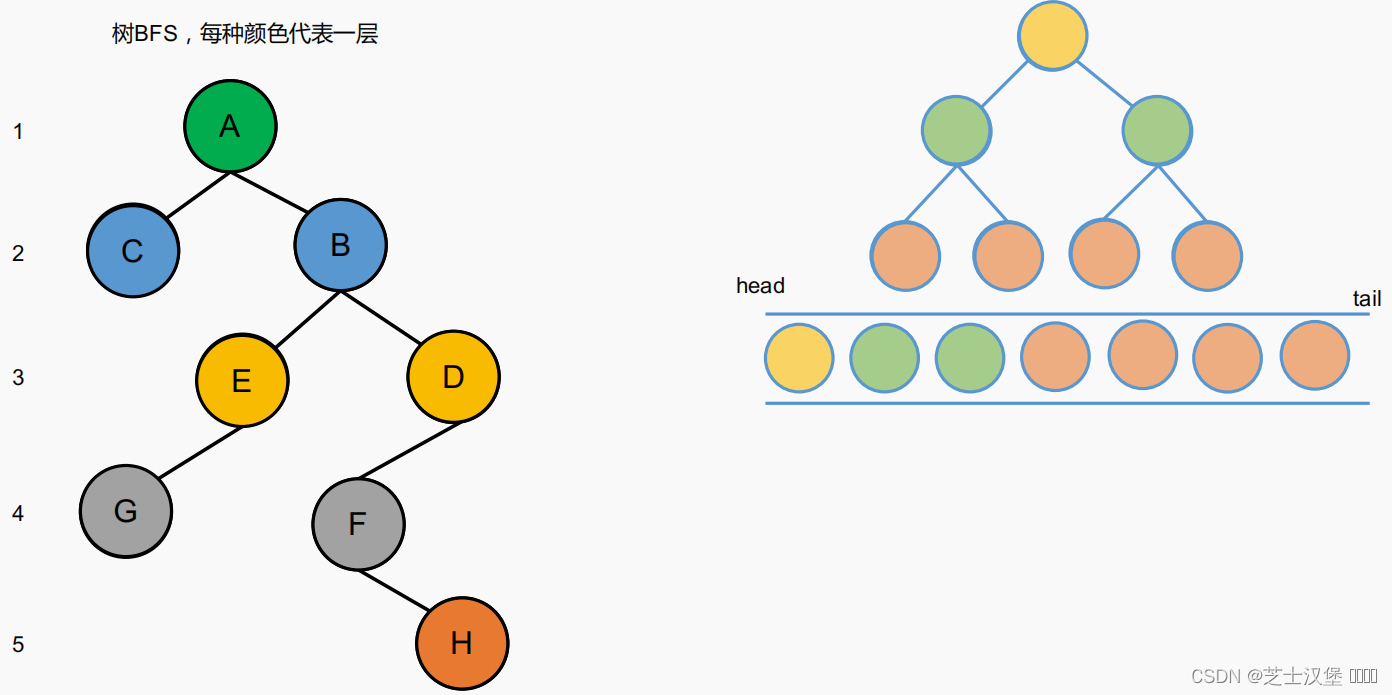
图的BFS
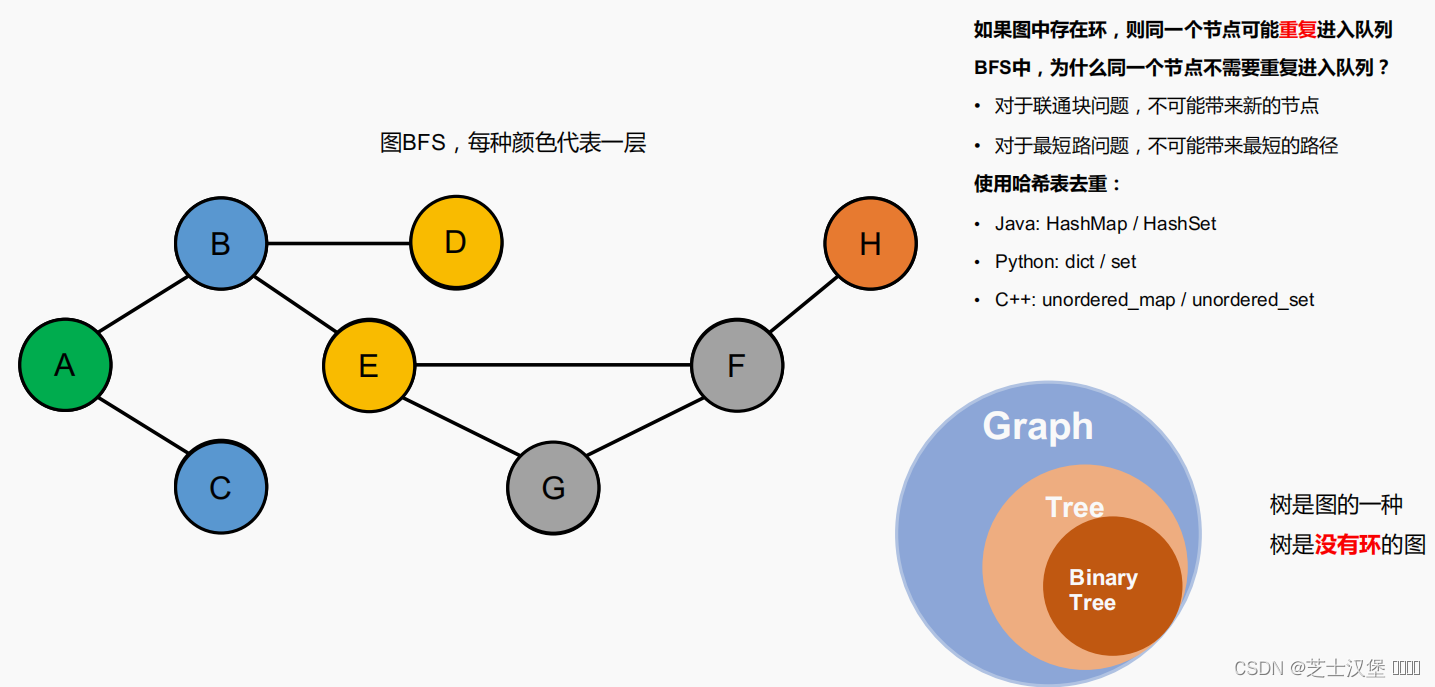
解决最短路径的管法有哪些
| 简单图 | 复杂图 |
|---|---|
| BFS | SPFA, Floyd, Dijkstra, Bellman-ford面试中一般不考复杂图最短路径问题 |
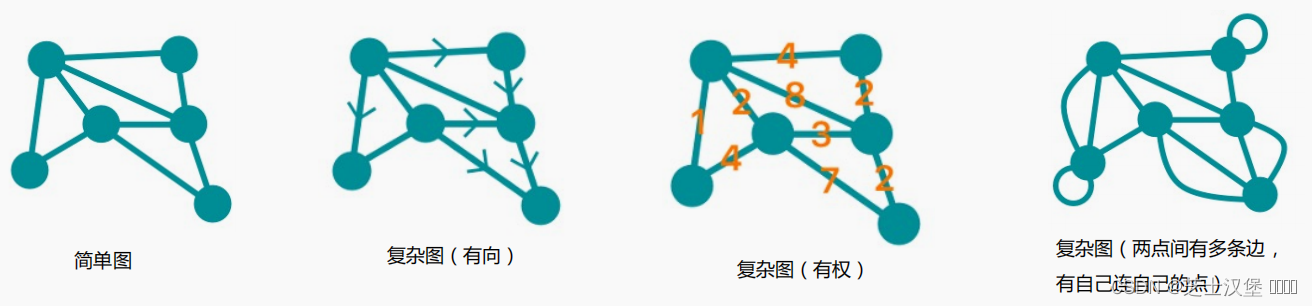
什么是简单图
? 没有方向 (undirected)
? 没有权重 (unweighted)
? 两点之间最多只有一条边 (no multiple edges)
? 一个点没有一条边直接连着自己 (no graph loops,这里的graph loop指的是自己直接指向自己的loop)
BFS 算法的通用模板
Queue<Node> queue = new ArrayDeque<>();
HashMap<Node, Integer> distance = new HashMap<>();
//step1:初始化
//把初始节点放到queue里如果有多个就都放进去
//1并标记初始节点的距离为记录在distance的hashmap里
//distance有两个作用,一是判断是否已经访问过,二是记录离起点的距离
queue.offer(node);
distance.put(node, 0);
//step2:不断访问队列
//while循环+每次pop队列中的一个点出来
while (!queue.isEmpty()) {
Node node = queue.poll();
//step3:拓展相邻节点
//pop出的节点的相邻节点,加入队列并在distance中存储距离
for (Node neighbor : node.getNeighbors()) {
if (distance.containsKey(neighbor)) {
continue;
}
distance.put(neighbor, distance.get(node) + 1);
queue.offer(neighbor);
}
}
题例
克隆一张无向图. 无向图的每个节点包含一个 label 和一个列表 neighbors. 保证每个节点的 label 互不相同.
你的程序需要返回一个经过深度拷贝的新图. 新图和原图具有同样的结构, 并且对新图的任何改动不会对原图造成任何影响
你需要返回与给定节点具有相同 label 的那个节点
输入
{1,2,4#2,1,4#4,1,2}
输出
{1,2,4#2,1,4#4,1,2}
解释
1 => 2, 4
2 => 1, 4
4 => 1, 2
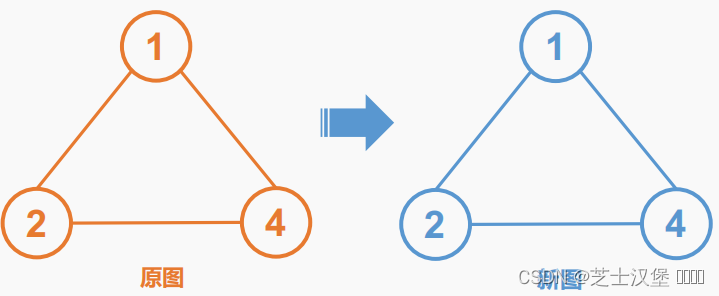
原图和新图的点和边一模一样
题解
将整个算法分解为三个步骤:1.找到所有点 2.复制所有点 3.复制所有边
/**
* Definition for Undirected graph.
* class UndirectedGraphNode {
* int label;
* List<UndirectedGraphNode> neighbors;
* UndirectedGraphNode(int x) {
* label = x;
* neighbors = new ArrayList<UndirectedGraphNode>();//label的邻居
* }
* }
*/
public class Solution {
/**
* @param node: A undirected graph node
* @return: A undirected graph node
*/
public UndirectedGraphNode cloneGraph(UndirectedGraphNode node) {
// write your code here
if (node == null) {
return null;
}
//第一步:找到所有点
List<UndirectedGraphNode> nodes = findNodesByBFS(node);
//第二步:复制所有点
Map<UndirectedGraphNode, UndirectedGraphNode> mapping = copyNodes(nodes);
//第三步:复制所有边
copyEdges(nodes, mapping);
//返回与给定节点具有相同 label 的那个点
return mapping.get(node);
}
//第一步:BFS找到所有点
private List<UndirectedGraphNode> findNodesByBFS(UndirectedGraphNode node) {
Queue<UndirectedGraphNode> queue = new LinkedList<>();
//保存所有的点,不重不漏
Set<UndirectedGraphNode> visited = new HashSet<>();
queue.offer(node);
visited.add(node);
while (!queue.isEmpty()) {
UndirectedGraphNode curNode = queue.poll();
for (UndirectedGraphNode neighbor : curNode.neighbors) {
//如果之前已经找到了这个点,无需再次BFS,否则死循环
if (visited.contains(neighbor)) {
continue;
}
visited.add(neighbor);
queue.offer(neighbor);
}
}
return new LinkedList<>(visited);
}
//第二步:复制所有点
private Map<UndirectedGraphNode, UndirectedGraphNode> copyNodes(List<UndirectedGraphNode> nodes) {
//旧点->新点的映射
Map<UndirectedGraphNode, UndirectedGraphNode> mapping = new HashMap<>();
for (UndirectedGraphNode node : nodes) {
mapping.put(node, new UndirectedGraphNode(node.label));
}
return mapping;
}
//第三步:复制所有边
private void copyEdges(List<UndirectedGraphNode> nodes, Map<UndirectedGraphNode, UndirectedGraphNode> mapping){
for (UndirectedGraphNode node : nodes) {
UndirectedGraphNode newNode = mapping.get(node);
//旧点有哪些邻居,新点就有那些邻居
for (UndirectedGraphNode neighbor : node.neighbors) {
UndirectedGraphNode newNeighbor = mapping.get(neighbor);
newNode.neighbors.add(newNeighbor);
}
}
}
}
题例
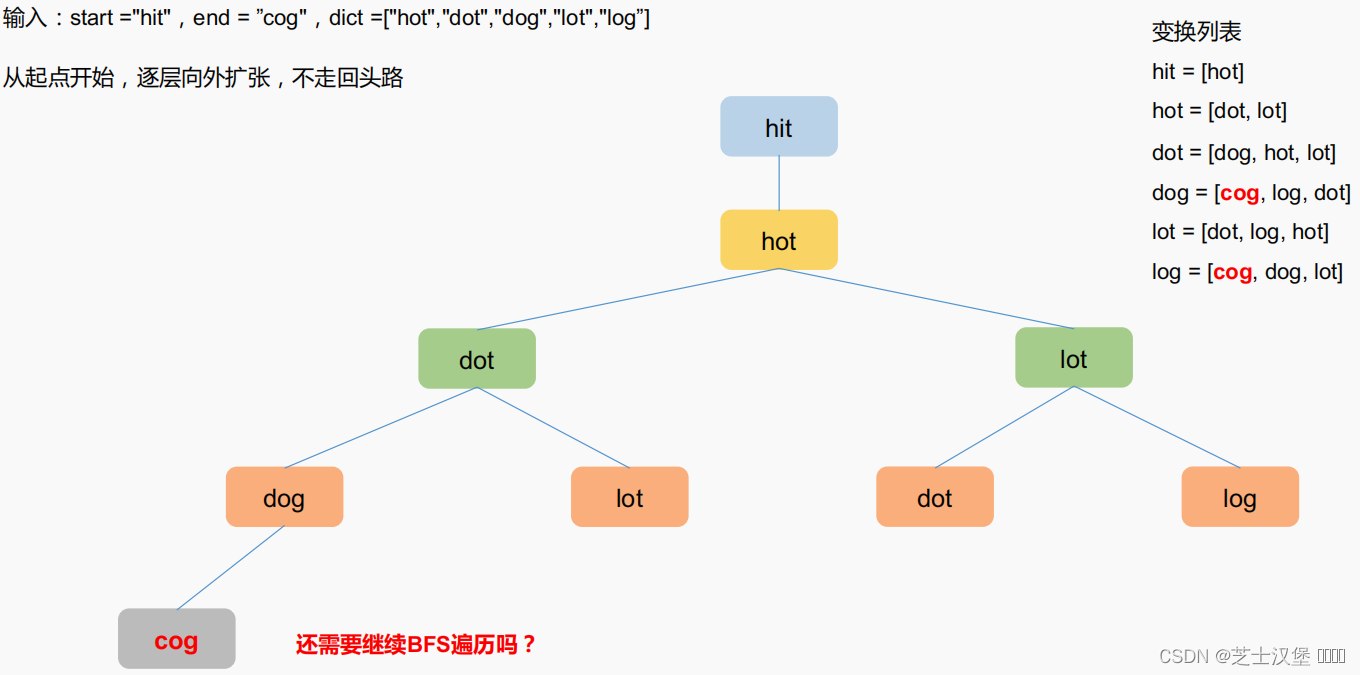
出两个单词(start和end)和一个字典,找出从start到end的最短转换序列,输出最短序列的长度。
变换规则如下:
每次只能改变一个字母。
变换过程中的中间单词必须在字典中出现。(起始单词和结束单词不需要出现在字典中)
样例
输入:
start = "a"
end = "c"
dict =["a","b","c"]
输出:
2
解释:
"a"->"c"
题解一
public class Solution {
/**
* @param start: a string
* @param end: a string
* @param dict: a set of string
* @return: An integer
*/
public int ladderLength(String start, String end, Set<String> dict) {
// 假设dict不为null
// 假设beginWord 和 endWord 是非空的,且二者不相同
// 必须加入end 可以加入start
dict.add(end);
HashSet<String> visited = new HashSet<String>();
Queue<String> queue = new LinkedList<String>();
queue.offer(start);
visited.add(start);
// 记录最短线长度,起始长度为1
int length = 1;
while (!queue.isEmpty()) {
// 到下一层的长度
length++;
// 当前层有size个元素
int size = queue.size();
for (int i = 0; i < size; i++) {
String word = queue.poll();
// 得到下一步的单词
for (String nextWord : getNextWords(word, dict)) {
if (visited.contains(nextWord)) {
continue;
}
// 如果下一层的词为尾词,直接返回当前到下一层的长度
if (nextWord.equals(end)) {
return length;
}
// 加入下一层,为后面BFS做准备
visited.add(nextWord);
queue.offer(nextWord);
}
}
}
// 不能实现首位接龙,返回0
return 0;
}
private ArrayList<String> getNextWords(String word, Set<String> dict) {
ArrayList<String> nextWords = new ArrayList<String>();
// 枚举字典中的每个词
for (String nextWord : dict) {
boolean hashOneDiff = false;
for (int i = 0; i < word.length(); i++) {
// 预判两个词是否只相差一个字母,如果是则可以接龙
if (nextWord.charAt(i) != word.charAt(i)) {
if (hashOneDiff) {
hashOneDiff = false;
break;
}
hashOneDiff = true;
}
}
if (hashOneDiff) {
nextWords.add(nextWord);
}
}
return nextWords;
}
// 在s中,把位置index的字母替换成c,返回替换后的字符串
private String replace(String s, int index, char c) {
char[] chars = s.toCharArray();
chars[index] = c;
return new String(chars);
}
}
可以对getNextWords进行优化
public class Solution {
/**
* @param start: a string
* @param end: a string
* @param dict: a set of string
* @return: An integer
*/
public int ladderLength(String start, String end, Set<String> dict) {
// 假设dict不为null
// 假设beginWord 和 endWord 是非空的,且二者不相同
// 必须加入end 可以加入start
dict.add(end);
HashSet<String> visited = new HashSet<String>();
Queue<String> queue = new LinkedList<String>();
queue.offer(start);
visited.add(start);
// 记录最短线长度,起始长度为1
int length = 1;
while (!queue.isEmpty()) {
// 到下一层的长度
length++;
// 当前层有size个元素
int size = queue.size();
for (int i = 0; i < size; i++) {
String word = queue.poll();
// 得到下一步的单词
for (String nextWord : getNextWords(word, dict)) {
if (visited.contains(nextWord)) {
continue;
}
// 如果下一层的词为尾词,直接返回当前到下一层的长度
if (nextWord.equals(end)) {
return length;
}
// 加入下一层,为后面BFS做准备
visited.add(nextWord);
queue.offer(nextWord);
}
}
}
// 不能实现首位接龙,返回0
return 0;
}
// 在s中,把位置index的字母替换成c,返回替换后的字符串
private String replace(String s, int index, char c) {
char[] chars = s.toCharArray();
chars[index] = c;
return new String(chars);
}
// 找到可以和word接龙的所有单词
// 比如 word = 'hot', dirt = {'hot', 'hit', 'hog'}, return {'hit', 'hog'}
private ArrayList<String> getNextWords(String word, Set<String> dict) {
ArrayList<String> nextWords = new ArrayList<String>();
// 枚举当前替换的字母
for (char c = 'a'; c <= 'z'; c++) {
// 枚举替换位置
for (int i = 0; i < word.length(); i++) {
if (c == word.charAt(i)) {
continue;
}
String nextWord = replace(word, i, c);
// 如果字母替换后的单词存在于dirt,加入nextWords
if (dict.contains(nextWord)) {
nextWords.add(nextWord);
}
}
}
return nextWords;
}
}
矩阵中的宽度优先搜索
描述
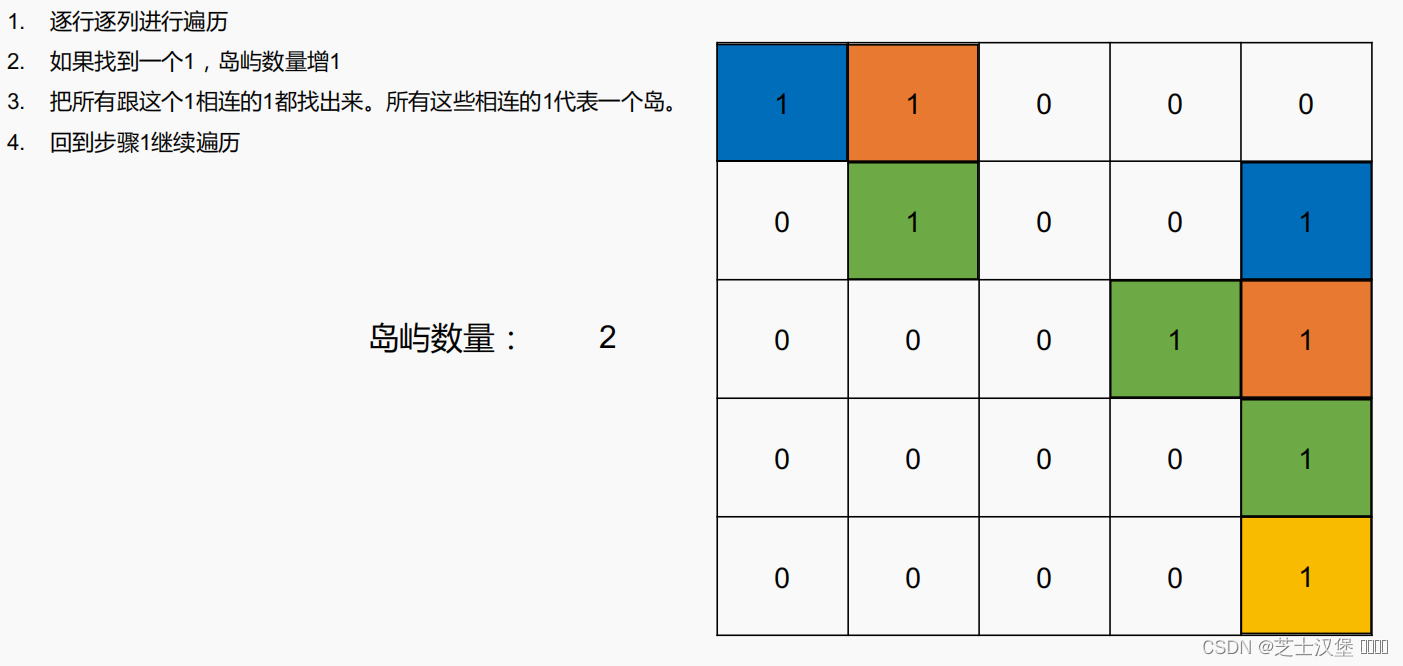
给一个 01 矩阵,求不同的岛屿的个数。
0 代表海,1 代表岛,如果两个 1 相邻,那么这两个 1 属于同一个岛。我们只考虑上下左右为相邻。
样例
输入:
[
[1,1,0,0,0],
[0,1,0,0,1],
[0,0,0,1,1],
[0,0,0,0,0],
[0,0,0,0,1]
]
输出:
3
题解
// 定义一个class,表示坐标系中的一点
class Coordinate {
int x, y;
public Coordinate(int x, int y) {
this.x = x;
this.y = y;
}
}
public class Solution {
/**
* @param grid: a boolean 2D matrix
* @return: an integer
*/
// 四个方向的偏移量
int[] deltaX = {0, 1, -1, 0};
int[] deltaY = {1, 0, 0, -1};
public int numIslands(boolean[][] grid) {
// 特殊性情况处理
if (grid == null || grid.length == 0 || grid[0] == null || grid[0].length == 0) {
return 0;
}
int islands = 0;
int row = grid.length, col = grid[0].length;
// 记录某点是否被BFS过, 如果之前已经被BFS过, 不应该再次被BFS
boolean[][] visited = new boolean[row][col];
// 遍历矩阵中的每一个点
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
// 如果为0,无需BFS
// 如果该点已经被visited,无需做冗余遍历,重复计算
if (grid[i][j] && !visited[i][j]) {
bfs(grid, i, j, visited);
islands++;
}
}
}
return islands;
}
// 从一块土地出发,通过BFS,遍历整个岛屿
private void bfs(boolean[][] grid, int x, int y, boolean[][] visited) {
Queue<Coordinate> queue = new ArrayDeque<>();
queue.offer(new Coordinate(x, y));
visited[x][y] = true;
while (!queue.isEmpty()) {
Coordinate coor = queue.poll();
// 遍历上线左右四个方向
for (int direction = 0; direction < 4; direction++) {
int newX = coor.x + deltaX[direction];
int newY = coor.y + deltaY[direction];
if (!isVaild(grid, newX, newY, visited)) {
continue;
}
queue.offer(new Coordinate(newX, newY));
// 一旦入队,标记此点已经参与过BFS
visited[newX][newY] = true;
}
}
}
// 预判一个点是否可以进行BFS
private boolean isVaild(boolean[][] grid, int x, int y, boolean[][] visited) {
int n =grid.length, m = grid[0].length;
// 如果出界,返回false 0
if (x < 0 || x >= n || y < 0 || y >= m) {
return false;
}
// 如果已经BFS过,不再次BFS,避免 死循环 和 冗余的BFS的变量
if (visited[x][y]) {
return false;
}
// 如果是1,返回true,否则0为false
return grid[x][y];
}
}
拓扑排序 Topological Sorting
入度(In-degree):
有向图(Directed Graph)中指向当前节点的点的个数(或指向当前节点的边的条数)
算法描述:
- 统计每个点的入度
- 将每个入度为 0 的点放入队列(Queue)中作为起始节点
- 不断从队列中拿出一个点,去掉这个点的所有连边(指向其他点的边),其他点的相应的入度 - 1
- 一旦发现新的入度为 0 的点,丢回队列中
拓扑排序并不是传统的排序算法
一个图可能存在多个拓扑序(Topological Order),也可能不存在任何拓扑序
题例
你需要去上n门课才能获得offer,这些课被标号为 0 到 n-1 。有一些课程需要“前置课程”,比如如果你要上课程0,你需要先学课程1,我们用一个匹配来表示他们: [0,1]
给你课程的总数量和一些前置课程的需求,返回你为了学完所有课程所安排的学习顺序。
可能会有多个正确的顺序,你只要返回一种就可以了。如果不可能完成所有课程,返回一个空数组。
样例
输入: n = 2, prerequisites = [[1,0]]
输出: [0,1]
题解
统计每个点的入度
将每个入度为0的点放入队列(Queue)中作为起始节点。0、1入读均为0,所以可以把0、1(不分前后)入队列
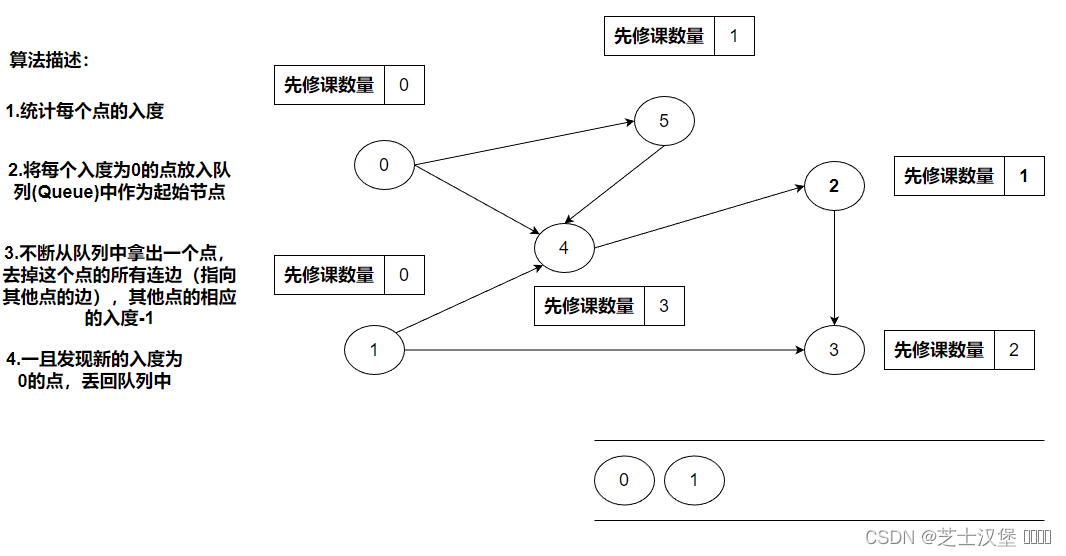
不断从队列中拿出一个点,去掉这个点的所有连边(指向其他点的边),其他点的相应的入度-1。0的连边为4、5相应的入度-1,此时4、5的度分别为为0、2.
一旦发现新的入读为零的点,将其入队。
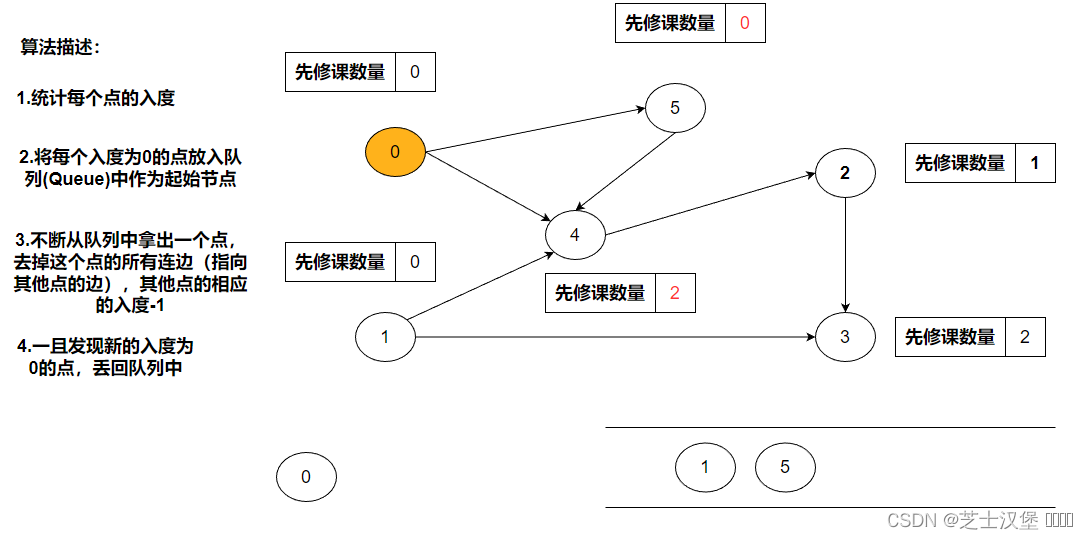
5出队后出现新的度为0的4,将其入队。
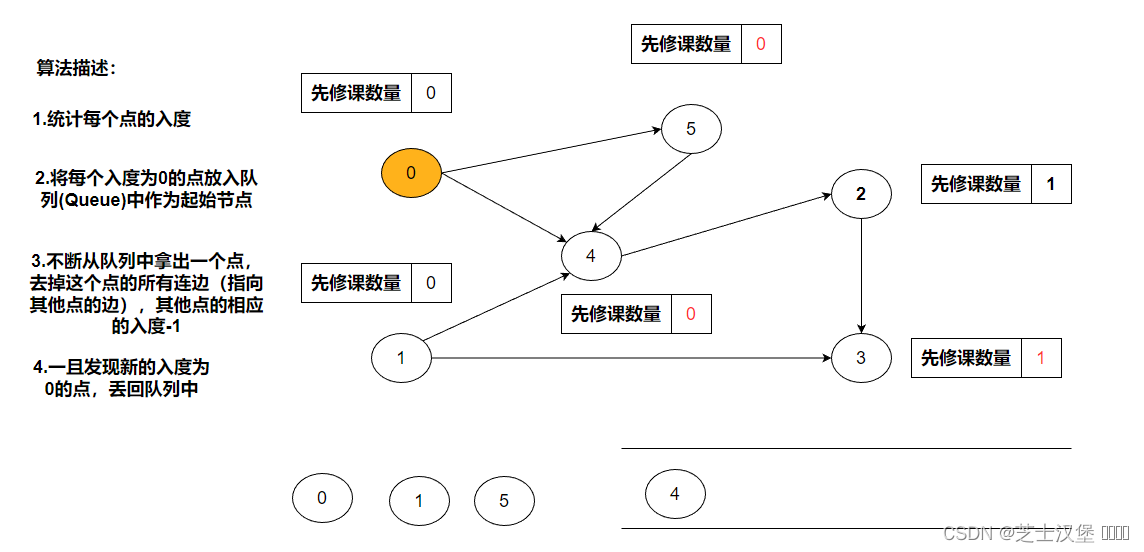
按上述规则进行,知道结束
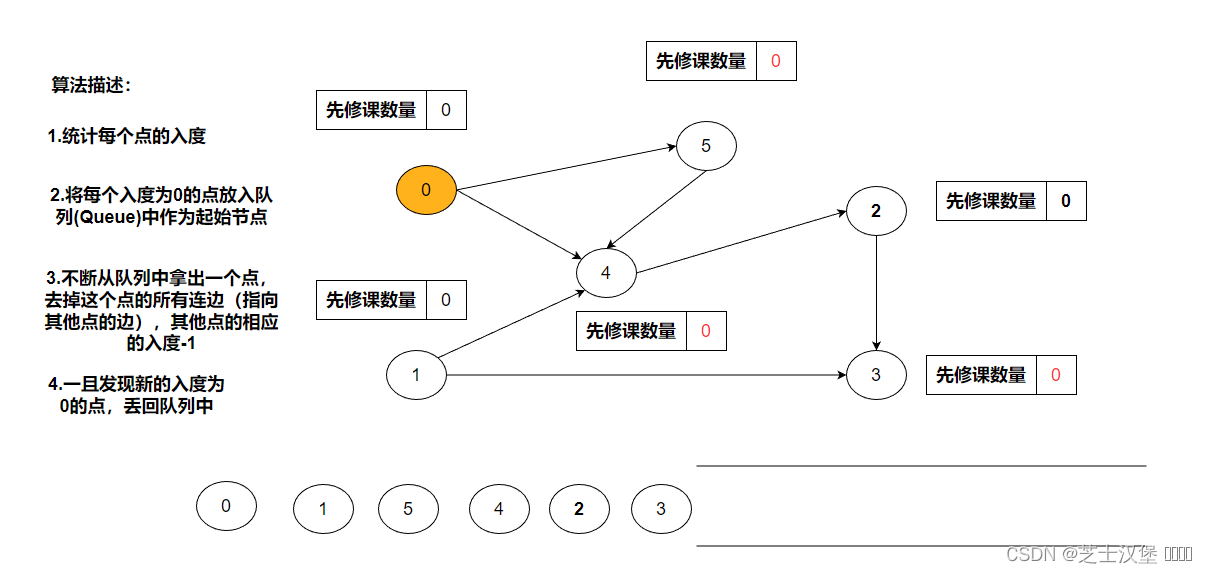
public class Solution {
/**
* @param numCourses: a total of n courses
* @param prerequisites: a list of prerequisite pairs
* @return: the course order
*/
public int[] findOrder(int numCourses, int[][] prerequisites) {
// 构建图,代表(先修课->多个后修课)的映射
List[] graph = new ArrayList[numCourses];
// 图的初始化,每个先修课->空后修课List
for (int i = 0; i < numCourses; i++) {
graph[i] = new ArrayList<Integer>();
}
// 1.统计每个点的入度,并构建图
int[] inDegree = new int[numCourses];
for (int[] edge : prerequisites) {
graph[edge[1]].add(edge[0]);
inDegree[edge[0]]++;
}
Queue queue = new LinkedList<>();
// 2.将每个入度为0的点放入队列(Queue)中作为起始节点
for (int i = 0; i < inDegree.length; i++) {
if (inDegree[i] == 0) {
queue.add(i);
}
}
// 记录已修课程的数量
int numChoose = 0;
// 记录拓扑顺序
int[] topoOrder = new int[numCourses];
// 3.不能从队列中拿出一个点,去掉这个点的所有连边(指向其他的边)其他点的相应的入度-1
while (!queue.isEmpty()) {
int nowPos = (int)queue.poll();
topoOrder[numChoose] = nowPos;
numChoose++;
for (int i = 0; i < graph[nowPos].size(); i++) {
int nextPos = (int)graph[nowPos].get(i);
// 当前点的邻居的入度减1,表示每个后修课的一门先修课已经完成
inDegree[nextPos]--;
// 4.一旦发现新的入读为0的点,丢回队列中
// 表示一门后修课的所有先修课已经完成了,可以被修了
if (inDegree[nextPos] == 0) {
queue.add(nextPos);
}
}
}
// 如果全部课程已经被修过,那么返回拓扑排序,否则返回空
return (numChoose == numCourses) ? topoOrder : new int[0];
}
}