1.完全二叉树与普通二叉树的对比
我们前面介绍过完全二叉树以及堆(一种完全二叉树)，并且实现了堆用顺序结构存储的数据结构。还介绍了两个基本算法：向上调整算法、向下调整算法。在此基础上使用堆解决了 Top-K 问题，以及堆排序。我们通过完全二叉树的规律可以发现，完全二叉树如果不看最后一层，那么它是一棵满二叉树；最后一层的节点必须是上一层连续节点并且依次是左孩子、右孩子。那么现在要介绍的是普通二叉树。普通二叉树只满足二叉树的基本定义，它不满足完全二叉树的定义。那么普通二叉树的结构可能是下面这几种：
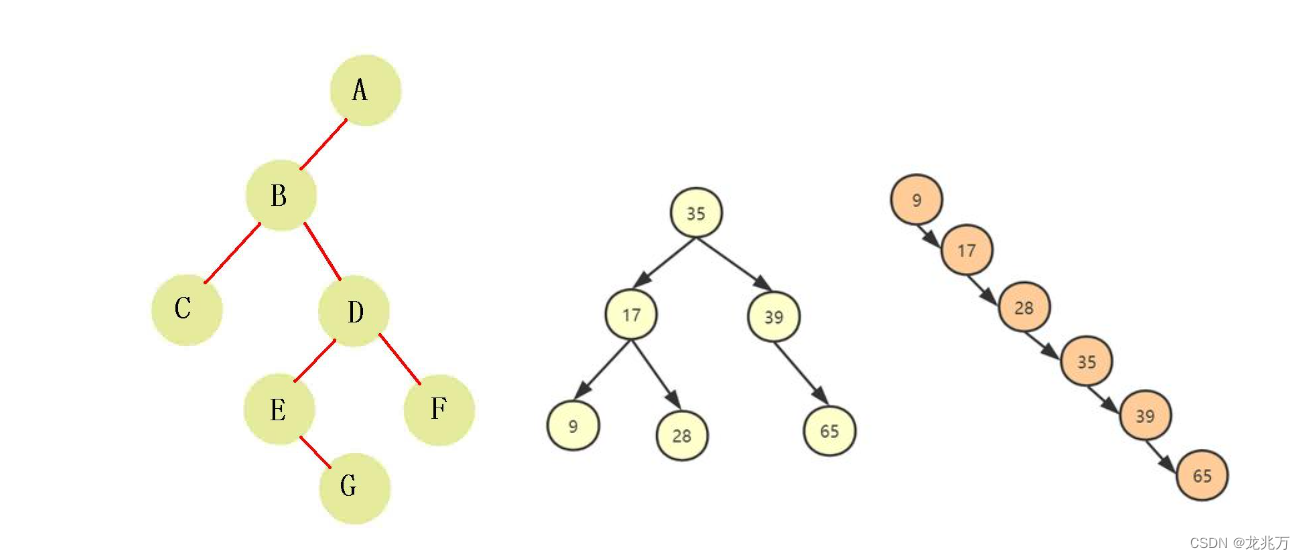
?可以发现普通二叉树的结构没有规律，如果用顺序结构存储的话那么物理空间不一定是连续的。
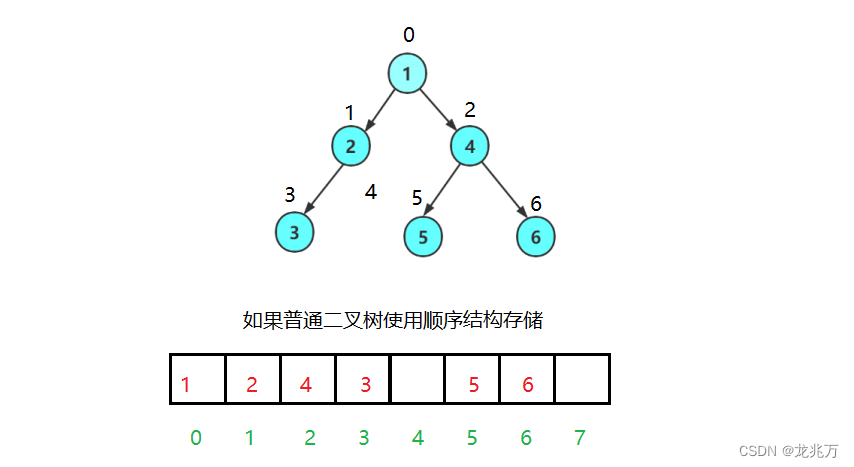
如果是这样，那么数据的存储就没有意义。我们可以试想一下，当我们真正进行数据存储的时候，我们会把数据不连续的存储起来吗？这样做的意义只有增加工作量、难度而已。?不单单是存储数据没有意义，就连删除也没有意义。我们想要访问二叉树的节点时候也是一个难题。所以普通二叉树我们一般使用链式结构，即用链表串联起来，需要注意，这样做的目的不是赋予它适合增删查改的能力，而是使用链式结构可以实现我们从来没有接触过的功能。例如二叉搜索树：
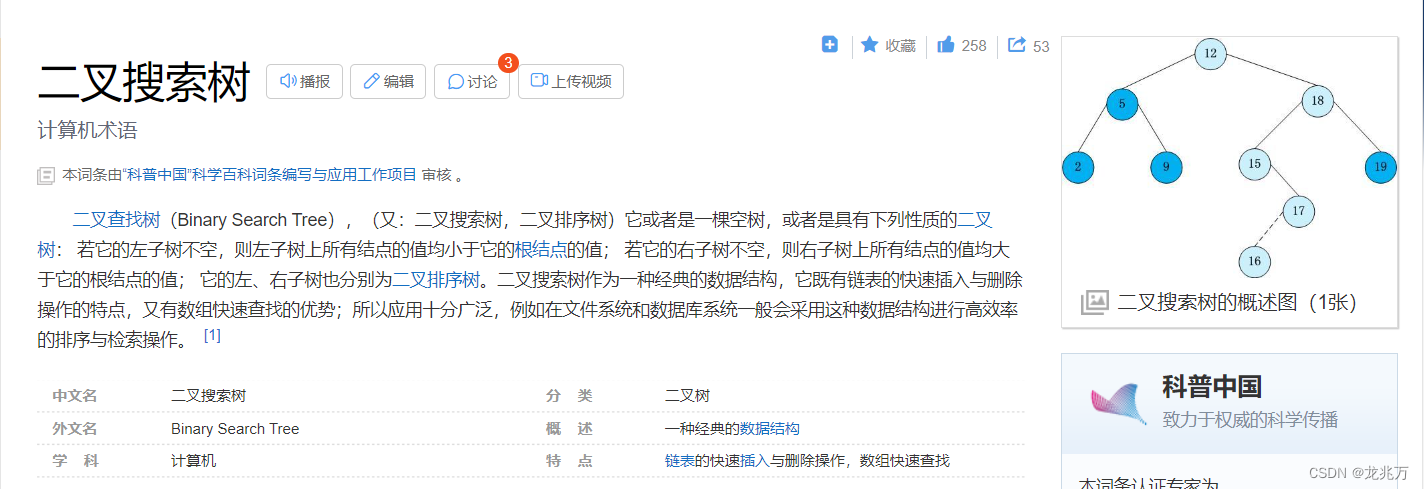
我们使用百科上面的例子做一个分析：
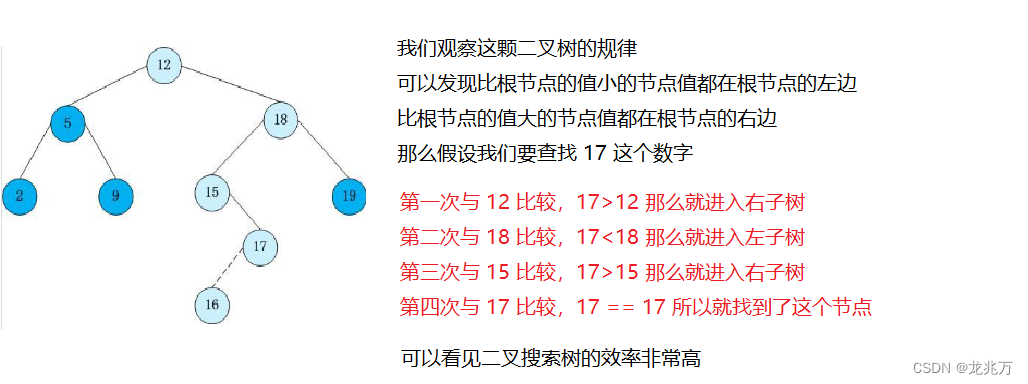?当然我们现在是简单的举一些普通二叉树的应用，本篇介绍的目的是为了打好基础，做好铺垫，为以后的学习打下地基。?
2.二叉树的性质
我们实现过堆用顺序结构存储的数据结构，里面也涉及到了不少的二叉树性质。那么现在将详细介绍二叉树的性质。
? ? ? ? 1.若规定根节点的层数为1，那么一颗非空二叉树的第k层最多有 2^(k-1) 个节点?
? ? ? ? 2.若规定根节点的层数为1，那么深度(高度)为h的二叉树最多一共有 2^h-1 个节点?
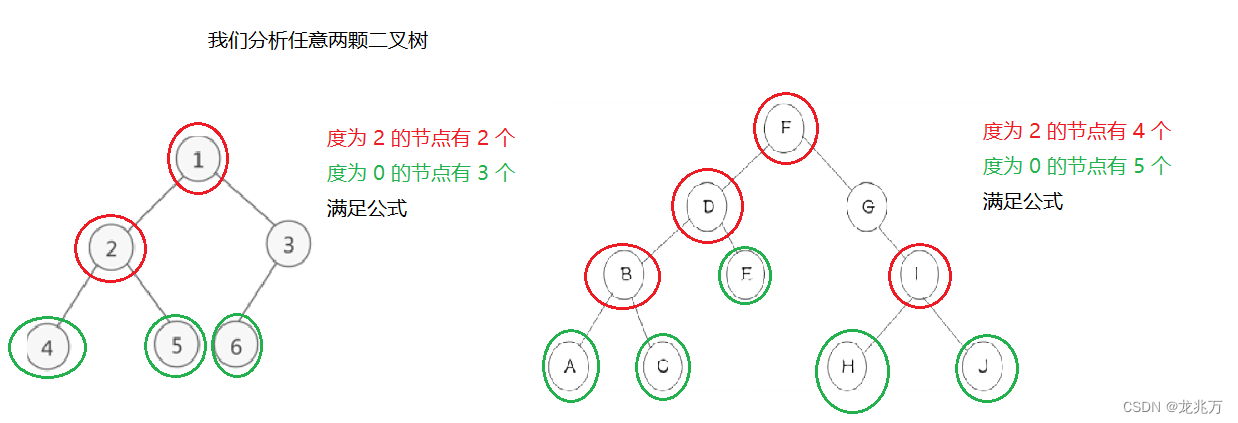
?????????3.对任意一颗二叉树而言，如果度为2的节点个数为n2，度为0的节点个数为n0，那么有n0=n2+1
?????????4.如果规定根节点的层数为1，那么总共有n个节点的满二叉树的深度就为h=log(n+1)
对应这条性质的解释就是数学公式，总节点数为 2^h-1 ,在这个表达式上计算 h ，就用到了对数。
? ? ? ? 5.在用顺序结构存储的完全二叉树中有下面几个规律：
? ? ? ? ? ? ? ? 1.如果 child != 0 ，那么 parent = (child-1)/2 ；如果 child = 0，那么这个节点为根节点
? ? ? ? ? ? ? ? 2.如果总节点个数为 n，假设 parent*2+1<n ，那么 parent*2+1 的值就是左孩子的下标
? ? ? ? ? ? ? ? 3.如果总节点个数为 n，假设 parent*2+2<n ，那么 parent*2+2 的值就是右孩子的下标
这三条性质在我们实现堆的顺序结构的时候使用过，当然也是基于数学上得来的公式。
2.1二叉树性质有关练习
1. 某二叉树共有 399 个结点，其中有 199 个度为 2 的结点，则该二叉树中的叶子结点数为（ ）A 不存在这样的二叉树B 200C 198D 199答案： A 。根据公式 n0=n2+1 可知，度为 0 的节点个数比度为 2 的节点个数多一个。
2. 下列数据结构中，不适合采用顺序存储结构的是（）A 非完全二叉树B 堆C 队列D 栈答案：A。即使队列不推荐使用顺序结构存储，但即使使用，也比非完全二叉树效率高。
3. 在具有 2n 个结点的完全二叉树中，叶子结点个数为（）A nB n+1C n-1D n/2答案： A 。在二叉树中，节点的分类只有三种，即度为2的节点，度为1的节点和度为0的节点。那么表达式就为 2n = n2+n1+n0 ，又因为 n2=n0+1 ，所以 2n = 2n0-1+n1；又因为 2n 的结果只能是整数，所以 n1 必须等于 1。故n0 = n。
4. 一棵完全二叉树的节点数位为 531 个，那么这棵树的高度为（）A 11B 10C 8D 12答案： B 。完全二叉树的节点个数在 [2^(h-1),2^h-1] 这个区间内。那么将 10 带入这个表达式之中，那么区间就为 [512,1023] ，恰好 531 在这个区间之内，所以高度为 10。
5. 一个具有 767 个节点的完全二叉树，其叶子节点个数为（）A 383B 384C 385D 386答案： B 。n2+n1+n0=767，因为n2=n0+1，所以得 2n0-1+n1=767，即2n0+n1=768，因为 2n0 的结果必为偶数，所以n1必为0( 完全二叉树特性，度为1的节点个数要不为0要不为1 )，所以n0=384。
3.二叉树的递归遍历
我们再回顾一下二叉树的性质，我们提到过二叉树是递归定义的。
在任意一颗二叉树中，只有两种可能：要不为空；要不就为根节点、左子树和右子树组成。?
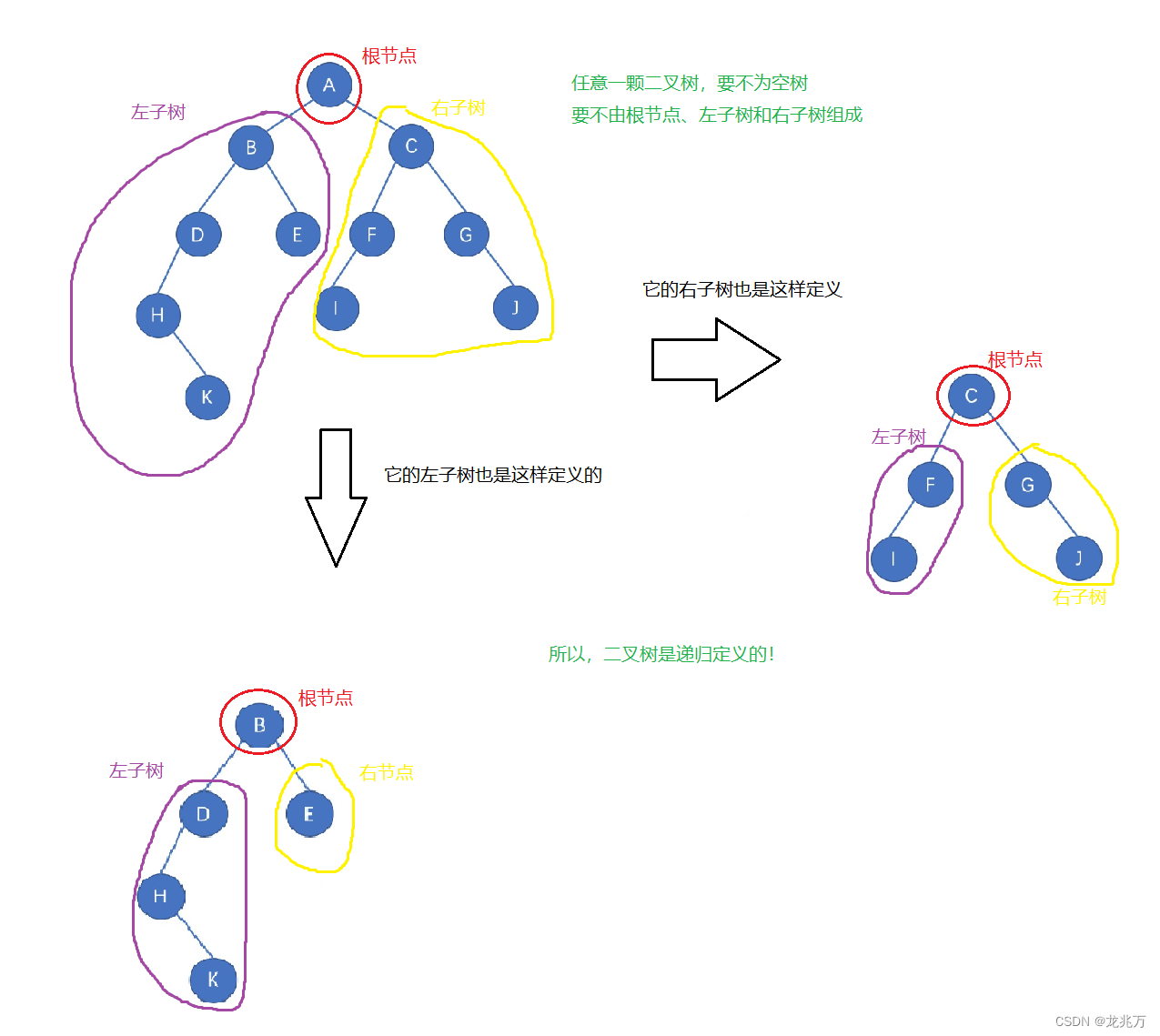
?了解了递归定义之后，我们就着手前序遍历、中序遍历和后序遍历。
- 前序遍历，在每一颗树中，它的遍历顺序总为：根节点、左子树、右子树。
- 中序遍历，在每一颗树中，它的遍历顺序总为：左子树、根节点、右子树。
- 后序遍历，在每一颗树中，它的遍历顺序总为：左子树、右子树、根节点。
注意我的用词，在每一颗树中。每一颗树，相当于左子树是一棵树，左子树当中又分为根节点、左子树和右子树，左子树的左子树又是一颗树，它又分为根节点、左子树和右子树……
我们先画一下前序遍历的顺序图。
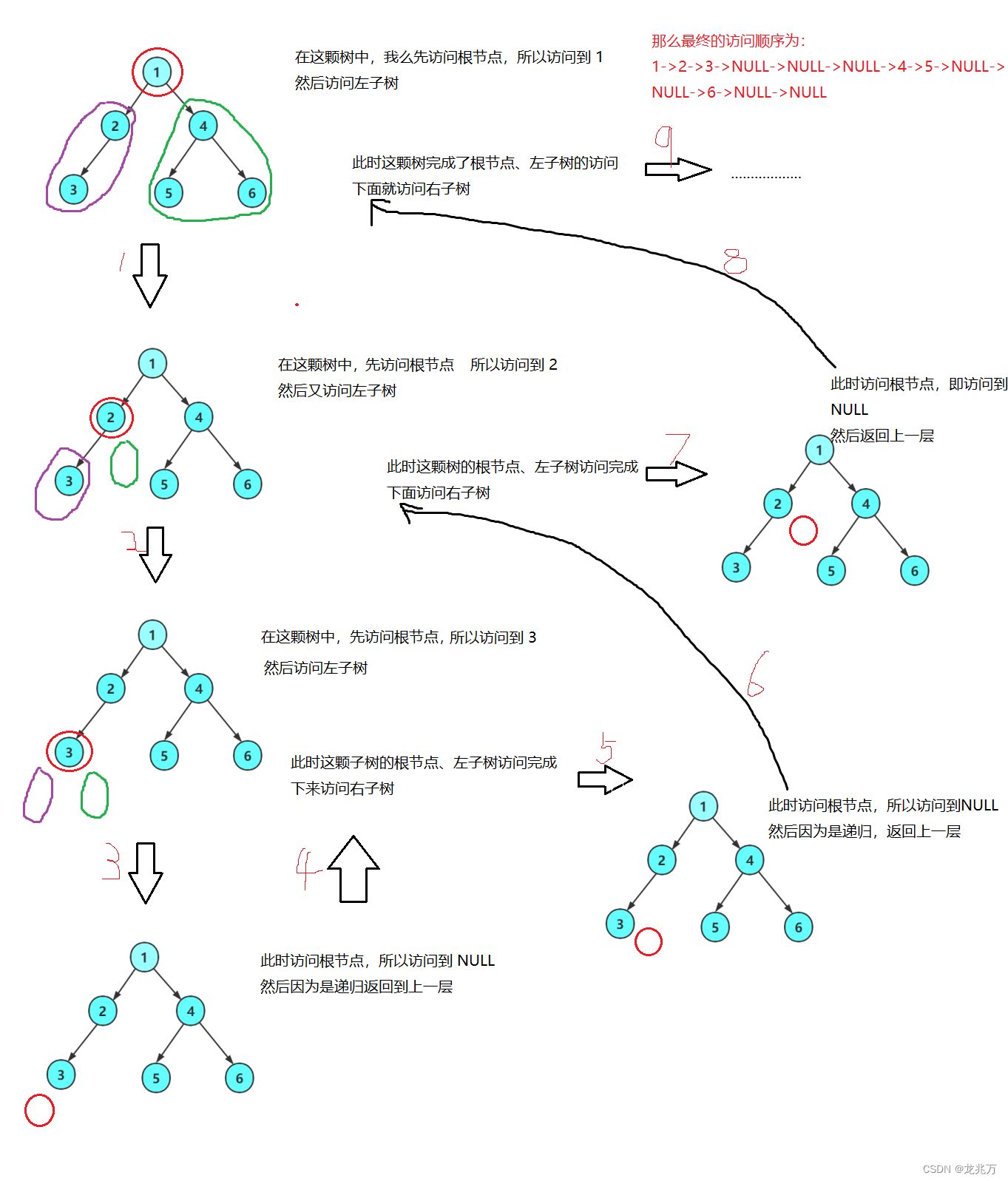
?就像这样层层递归，就可以完成遍历。那么中序遍历、后序遍历和前序遍历一样，那么这里的顺序图就省略了，我们直接看结果：
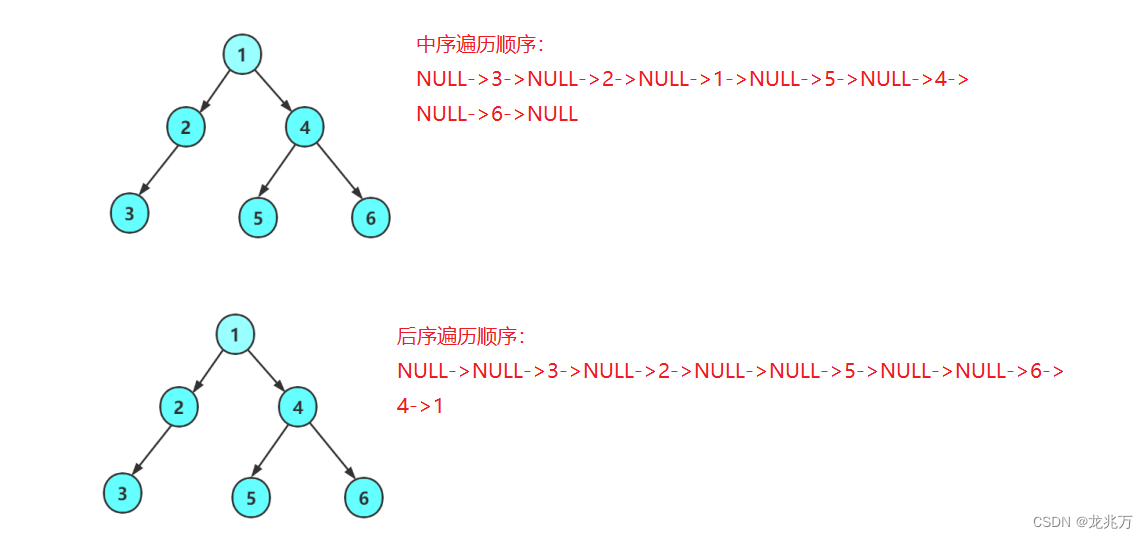
清楚了遍历顺序之后，就可以开始着手代码。这里注意，因为现在的部分是为了后续学习打基础，所以在这里手动构造与例子相同的二叉树。
#include <stdlib.h>
#include <assert.h>
#include <stdio.h>
typedef int BinaryData;
typedef struct Node
{
BinaryData val;
struct Node* left;
struct Node* right;
}Node;
Node* CreateNode()
{
Node* n1 = (Node*)malloc(sizeof(Node));
assert(n1);
Node* n2 = (Node*)malloc(sizeof(Node));
assert(n2);
Node* n3 = (Node*)malloc(sizeof(Node));
assert(n3);
Node* n4 = (Node*)malloc(sizeof(Node));
assert(n4);
Node* n5 = (Node*)malloc(sizeof(Node));
assert(n5);
Node* n6 = (Node*)malloc(sizeof(Node));
assert(n6);
n1->val = 1;
n2->val = 2;
n3->val = 3;
n4->val = 4;
n5->val = 5;
n6->val = 6;
n1->left = n2;
n1->right = n4;
n2->left = n3;
n2->right = NULL;
n3->left = NULL;
n3->right = NULL;
n4->left = n5;
n4->right = n6;
n5->left = NULL;
n5->right = NULL;
n6->left = NULL;
n6->right = NULL;
return n1;
}
//前序遍历
void PreTraval(Node* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
printf("%d ", root->val);
PreTraval(root->left);
PreTraval(root->right);
}
//中序遍历
void MidTraval(Node* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
MidTraval(root->left);
printf("%d ", root->val);
MidTraval(root->right);
}
//后序遍历
void PosTraval(Node* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
PosTraval(root->left);
PosTraval(root->right);
printf("%d ", root->val);
}
int main()
{
Node* root = CreateNode();
PreTraval(root);
printf("\n");
MidTraval(root);
printf("\n");
PosTraval(root);
printf("\n");
return 0;
}
4.递归遍历的衍生问题
了解了遍历之后，现在有很多衍生问题：怎么求节点个数？怎么求第k层的节点个数？如何求叶节点个数？如何查找值为x的节点？
4.1节点个数
我们逐个分析，如何求节点个数。求个数呢，通用方法是计数法，那么计数法在我们的递归上面也可以使用。
//求节点个数
int count = 0;//使用全局变量
int NodeSize(Node* root)
{
if (root == NULL)
{
return 0;
}
//static int count = 0;//使用static修饰的静态变量
count++;
NodeSize(root->left);
NodeSize(root->right);
return count;
}
int main()
{
Node* root = CreateNode();
/*PreTraval(root);
printf("\n");
MidTraval(root);
printf("\n");
PosTraval(root);
printf("\n");*/
printf("NodeSize = %d\n", NodeSize(root));
printf("NodeSize = %d\n", NodeSize(root));
return 0;
}
可以看到我们使用计数法是可以帮助我们完成任务的，但是当我们第二次调用这个函数就出现了问题。原因是全局变量和static修饰的静态变量只能被初始化一次。所以我们的计数方法是不够好的，那我们就要着手递归的方法了。
//求节点个数
int NodeSize(Node* root)
{
if (root == NULL)
{
return 0;
}
return NodeSize(root->left) + NodeSize(root->right) + 1;
}
//int count = 0;//使用全局变量
//int NodeSize(Node* root)
//{
// if (root == NULL)
// {
// return 0;
// }
// //static int count = 0;//使用static修饰的静态变量
// count++;
// NodeSize(root->left);
// NodeSize(root->right);
// return count;
//}
int main()
{
Node* root = CreateNode();
/*PreTraval(root);
printf("\n");
MidTraval(root);
printf("\n");
PosTraval(root);
printf("\n");*/
printf("NodeSize = %d\n", NodeSize(root));
printf("NodeSize = %d\n", NodeSize(root));
return 0;
}
可以看到，递归的方式完美的解决了计数的"BUG"。
4.2第k层的节点个数
通过公式我们就可以发现，k是一定要被减1的，那么在递归当中也不例外。既然是要求某一层的节点个数，我们只要加一个条件：即递归到了指定层数的时候，才有返回值。?
//求第k层的节点个数
int KSize(Node* root,int k)
{
assert(k > 0);//层数大于0才有意义
if (root == NULL)
{
return 0;
}
//加一个特定条件，必须在这一层才具有返回值
if (k == 1)
{
return 1;
}
//否则继续往下递归找到指定层数
return KSize(root->left,k-1) + KSize(root->right,k-1);
}
int main()
{
Node* root = CreateNode();
/*PreTraval(root);
printf("\n");
MidTraval(root);
printf("\n");
PosTraval(root);
printf("\n");*/
//printf("NodeSize = %d\n", NodeSize(root));
//printf("NodeSize = %d\n", NodeSize(root));
printf("KSize = %d\n", KSize(root, 3));
printf("KSize = %d\n", KSize(root, 1));
return 0;
}
4.3求叶节点个数
叶节点的特征为度为0，即左右孩子都为空。不言而喻，需要添加一个条件来具有返回值。
//求叶节点的个数
int LeafSize(Node* root)
{
if (root == NULL)
{
return 0;
}
if (root->left == NULL && root->right == NULL)
{
return 1;
}
return LeafSize(root->left) + LeafSize(root->right);
}
int main()
{
Node* root = CreateNode();
/*PreTraval(root);
printf("\n");
MidTraval(root);
printf("\n");
PosTraval(root);
printf("\n");*/
//printf("NodeSize = %d\n", NodeSize(root));
//printf("NodeSize = %d\n", NodeSize(root));
//printf("KSize = %d\n", KSize(root, 3));
//printf("KSize = %d\n", KSize(root, 1));
printf("LeafSize = %d\n", LeafSize(root));
return 0;
}?
4.4查找值为x的节点
很明显，我们需要添加一个条件来限定返回值。那么其难点在于，如果左子树当中找到了节点，那么右子树就不要遍历了；如果左子树当中没有找到指定节点才需要遍历右子树。如果左右子树都找不到指定节点才返回空。这时就要用到分治的思想。?
//查找值为x的节点
Node* NodeFind(Node* root, int x)
{
if (root == NULL)
{
return NULL;
}
if (root->val == x)
{
return root;
}
Node* LeftRet = NodeFind(root->left, x);
if (LeftRet != NULL)
{
return LeftRet;
}
Node* RightRet = NodeFind(root->right, x);
if (RightRet != NULL)
{
return RightRet;
}
return NULL;
}
int main()
{
Node* root = CreateNode();
/*PreTraval(root);
printf("\n");
MidTraval(root);
printf("\n");
PosTraval(root);
printf("\n");*/
//printf("NodeSize = %d\n", NodeSize(root));
//printf("NodeSize = %d\n", NodeSize(root));
//printf("KSize = %d\n", KSize(root, 3));
//printf("KSize = %d\n", KSize(root, 1));
//printf("LeafSize = %d\n", LeafSize(root));
printf("NodeFind = %p\n", NodeFind(root, 1));
printf("NodeFind = %p\n", NodeFind(root, 3));
printf("NodeFind = %p\n", NodeFind(root, 100));
return 0;
}4.5二叉树的销毁
二叉树的销毁，就是销毁所有的节点。后序遍历是非常契合的。
//二叉树销毁
void BinaryDestroy(Node* root)
{
if (root == NULL)
{
return;
}
BinaryDestroy(root->left);
BinaryDestroy(root->right);
free(root);
}5.二叉树的非递归遍历
5.1层序遍历
我们可以发现，上面提到的前序、中序、后序遍历好像都在往深的地方走，走到无路可走再退回到上一层继续往深的地方走。由此我们可以总结，前序、中序、后序遍历它们都是一种深度优先遍历(DFS)。现在我们要介绍二叉树的非递归遍历，即层序遍历。层序遍历是一种广度优先遍历(BFS)。?
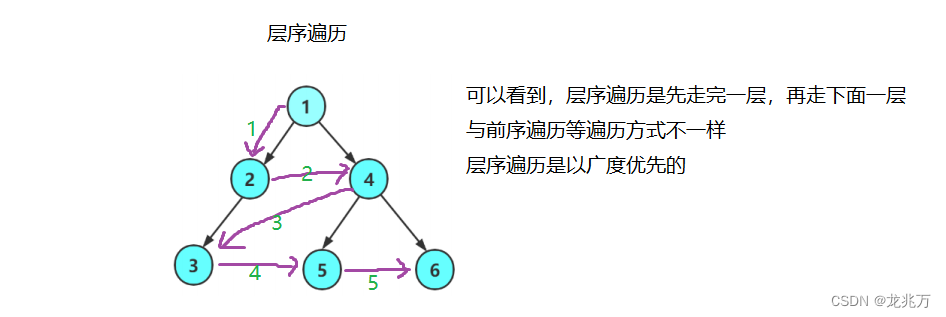
?那么层序遍历实现的思路是怎么样的呢？我们需要借助一个工具——队列。我们看图：
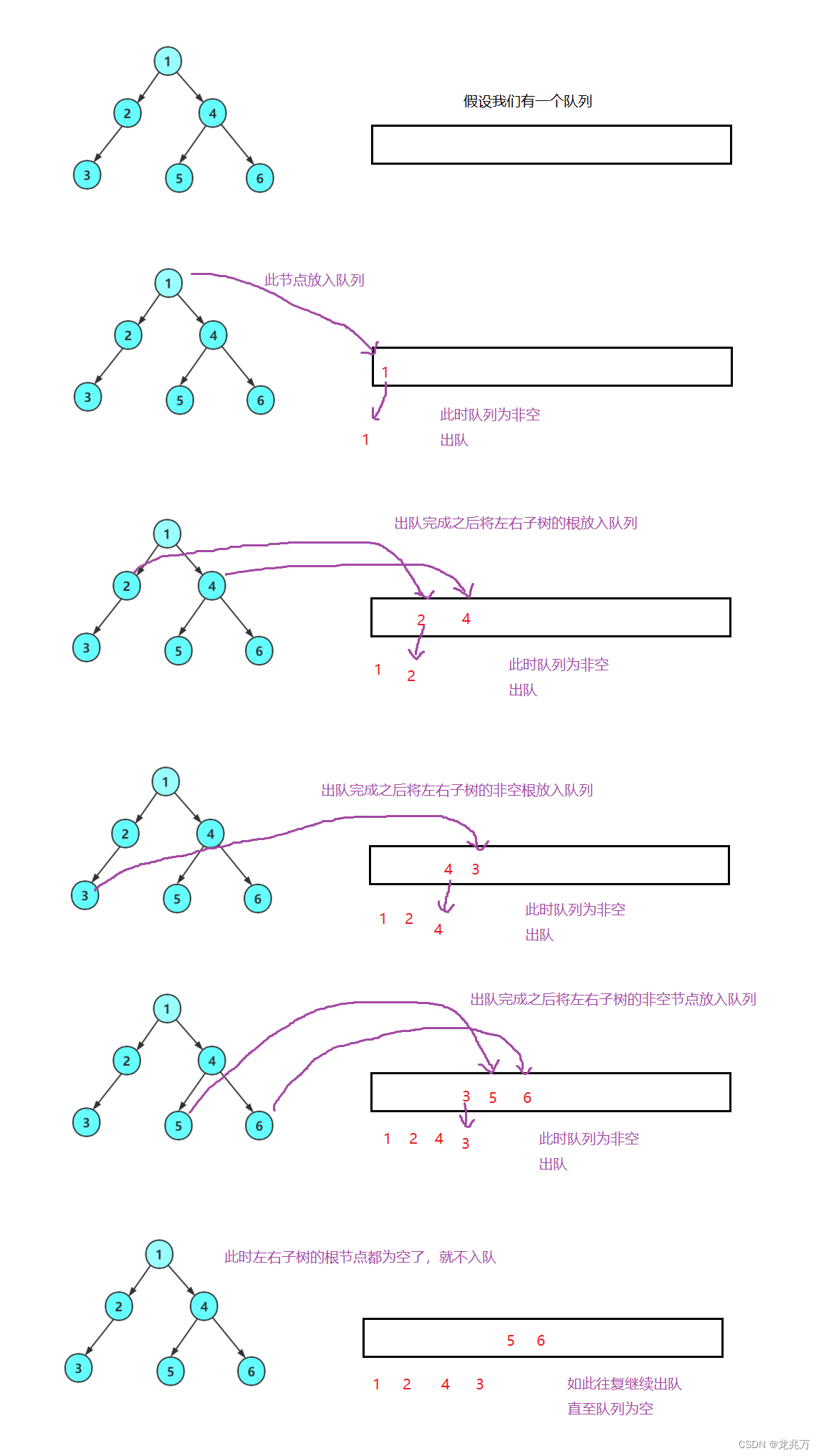
那么我们上手代码时要注意，在C语言的库中没有队列这个数据结构，所以我们需要将实现队列的代码CV过来。这个问题在C++中会得到解决。那么代码我们就可以这么写：
//层序遍历
void LayerTraval(Node* root)
{
HeadTail q;
QueueInit(&q);
//为空则为空树
if (root == NULL)
{
return;
}
//非空则入队列
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
Node* tmp = QueueHead(&q);
QueuePop(&q);
printf("%d ", tmp->val);
if (tmp->left != NULL)
{
QueuePush(&q, tmp->left);
}
if (tmp->right != NULL)
{
QueuePush(&q, tmp->right);
}
}
QueueDestroy(&q);
}
int main()
{
Node* root = CreateNode();
/*PreTraval(root);
printf("\n");
MidTraval(root);
printf("\n");
PosTraval(root);
printf("\n");*/
//printf("NodeSize = %d\n", NodeSize(root));
//printf("NodeSize = %d\n", NodeSize(root));
//printf("KSize = %d\n", KSize(root, 3));
//printf("KSize = %d\n", KSize(root, 1));
//printf("LeafSize = %d\n", LeafSize(root));
//printf("NodeFind = %p\n", NodeFind(root, 1));
//printf("NodeFind = %p\n", NodeFind(root, 3));
//printf("NodeFind = %p\n", NodeFind(root, 100));
LayerTraval(root);
return 0;
}
6.层序遍历的衍生问题
6.1判断二叉树是否为完全二叉树
碰到问题我们大胆地去想，首先便是通过节点个数能不能确定二叉树是否为完全二叉树。答案很明显不可能，因为完全二叉树的最后一层需要保证节点是连续的。但是这个方法是可以确定满二叉树的。
既然我们要通过层序遍历，那我们试着遍历任意几颗完全二叉树寻找规律：
?我们遍历两颗普通二叉树：
可以发现一个非常明显的规律，即完全二叉树使用层序遍历的结果 NULL 总为连续的；而普通二叉树使用层序遍历的结果 NULL 是不连续的。?
那么这个规律，便是我们代码的突破口。
//判断是否为完全二叉树
bool FuncTree(Node* root)
{
HeadTail q;
QueueInit(&q);
if (root == NULL)
{
return;
}
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
Node* tmp = QueueHead(&q);
QueuePop(&q);
//一旦拿到空，就跳出循环进行判断
//此时队列后面要不有节点，要不为空
//不用担心二叉树的所有节点是否完全存放在队列里面
if (tmp == NULL)
{
break;
}
QueuePush(&q, tmp->left);
QueuePush(&q, tmp->right);
}
while (!QueueEmpty(&q))
{
Node* tmp = QueueHead(&q);
QueuePop(&q);
if (tmp != NULL)
{
return false;
}
}
QueueDestroy(&q);
return true;
}
int main()
{
Node* root = CreateNode();
/*PreTraval(root);
printf("\n");
MidTraval(root);
printf("\n");
PosTraval(root);
printf("\n");*/
//printf("NodeSize = %d\n", NodeSize(root));
//printf("NodeSize = %d\n", NodeSize(root));
//printf("KSize = %d\n", KSize(root, 3));
//printf("KSize = %d\n", KSize(root, 1));
//printf("LeafSize = %d\n", LeafSize(root));
//printf("NodeFind = %p\n", NodeFind(root, 1));
//printf("NodeFind = %p\n", NodeFind(root, 3));
//printf("NodeFind = %p\n", NodeFind(root, 100));
//LayerTraval(root);
printf("FuncTree = %d\n", FuncTree(root));
return 0;
}
?8.结尾
为了方便，我把完整代码放在这里(队列各接口除外)。
//队列的声明
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>
#include <stdio.h>
typedef int BinaryData;
typedef struct Node
{
BinaryData val;
struct Node* left;
struct Node* right;
}Node;
//链表的结点
typedef Node* QueueData;
typedef struct QueueNode
{
QueueData val;
struct QueueNode* next;
}QueueNode;
//存储头、尾结点地址的指针
typedef struct HeadTail
{
QueueNode* head;
QueueNode* tail;
int size;//记录队列有几个元素
}HeadTail;
void QueueInit(HeadTail* p);//初始化队列
void QueuePush(HeadTail* p,QueueData x);//进入队列
QueueData QueueHead(HeadTail* p);//获取队头元素
QueueData QueueTail(HeadTail* p);//获取队尾元素
void QueuePop(HeadTail* p);//删除操作，出队
bool QueueEmpty(HeadTail* p);//检查队列是否为空
int QueueSize(HeadTail* p);//获取队列元素个数
void QueuePopTail(HeadTail* p);
void QueueDestroy(HeadTail* p);//销毁队列#include "Queue.h"
Node* CreateNode()
{
Node* n1 = (Node*)malloc(sizeof(Node));
assert(n1);
Node* n2 = (Node*)malloc(sizeof(Node));
assert(n2);
Node* n3 = (Node*)malloc(sizeof(Node));
assert(n3);
Node* n4 = (Node*)malloc(sizeof(Node));
assert(n4);
Node* n5 = (Node*)malloc(sizeof(Node));
assert(n5);
Node* n6 = (Node*)malloc(sizeof(Node));
assert(n6);
n1->val = 1;
n2->val = 2;
n3->val = 3;
n4->val = 4;
n5->val = 5;
n6->val = 6;
n1->left = n2;
n1->right = n4;
n2->left = n3;
n2->right = NULL;
n3->left = NULL;
n3->right = NULL;
n4->left = n5;
n4->right = n6;
n5->left = NULL;
n5->right = NULL;
n6->left = NULL;
n6->right = NULL;
return n1;
}
//前序遍历
void PreTraval(Node* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
printf("%d ", root->val);
PreTraval(root->left);
PreTraval(root->right);
}
//中序遍历
void MidTraval(Node* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
MidTraval(root->left);
printf("%d ", root->val);
MidTraval(root->right);
}
//后序遍历
void PosTraval(Node* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
PosTraval(root->left);
PosTraval(root->right);
printf("%d ", root->val);
}
//求节点个数
int NodeSize(Node* root)
{
if (root == NULL)
{
return 0;
}
return NodeSize(root->left) + NodeSize(root->right) + 1;
}
//int count = 0;//使用全局变量
//int NodeSize(Node* root)
//{
// if (root == NULL)
// {
// return 0;
// }
// //static int count = 0;//使用static修饰的静态变量
// count++;
// NodeSize(root->left);
// NodeSize(root->right);
// return count;
//}
//求第k层的节点个数
int KSize(Node* root,int k)
{
assert(k > 0);//层数大于0才有意义
if (root == NULL)
{
return 0;
}
//加一个特定条件，必须在这一层才具有返回值
if (k == 1)
{
return 1;
}
//否则继续往下递归找到指定层数
return KSize(root->left,k-1) + KSize(root->right,k-1);
}
//求叶节点的个数
int LeafSize(Node* root)
{
if (root == NULL)
{
return 0;
}
if (root->left == NULL && root->right == NULL)
{
return 1;
}
return LeafSize(root->left) + LeafSize(root->right);
}
//查找值为x的节点
Node* NodeFind(Node* root, int x)
{
if (root == NULL)
{
return NULL;
}
if (root->val == x)
{
return root;
}
Node* LeftRet = NodeFind(root->left, x);
if (LeftRet != NULL)
{
return LeftRet;
}
Node* RightRet = NodeFind(root->right, x);
if (RightRet != NULL)
{
return RightRet;
}
return NULL;
}
//层序遍历
void LayerTraval(Node* root)
{
HeadTail q;
QueueInit(&q);
//为空则为空树
if (root == NULL)
{
return;
}
//非空则入队列
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
Node* tmp = QueueHead(&q);
QueuePop(&q);
printf("%d ", tmp->val);
if (tmp->left != NULL)
{
QueuePush(&q, tmp->left);
}
if (tmp->right != NULL)
{
QueuePush(&q, tmp->right);
}
}
QueueDestroy(&q);
}
//二叉树销毁
void BinaryDestroy(Node* root)
{
if (root == NULL)
{
return;
}
BinaryDestroy(root->left);
BinaryDestroy(root->right);
free(root);
}
//判断是否为完全二叉树
bool FuncTree(Node* root)
{
HeadTail q;
QueueInit(&q);
if (root == NULL)
{
return;
}
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
Node* tmp = QueueHead(&q);
QueuePop(&q);
//一旦拿到空，就跳出循环进行判断
//此时队列后面要不有节点，要不为空
//不用担心二叉树的所有节点是否完全存放在队列里面
if (tmp == NULL)
{
break;
}
QueuePush(&q, tmp->left);
QueuePush(&q, tmp->right);
}
while (!QueueEmpty(&q))
{
Node* tmp = QueueHead(&q);
QueuePop(&q);
if (tmp != NULL)
{
return false;
}
}
QueueDestroy(&q);
return true;
}
int main()
{
Node* root = CreateNode();
/*PreTraval(root);
printf("\n");
MidTraval(root);
printf("\n");
PosTraval(root);
printf("\n");*/
//printf("NodeSize = %d\n", NodeSize(root));
//printf("NodeSize = %d\n", NodeSize(root));
//printf("KSize = %d\n", KSize(root, 3));
//printf("KSize = %d\n", KSize(root, 1));
//printf("LeafSize = %d\n", LeafSize(root));
//printf("NodeFind = %p\n", NodeFind(root, 1));
//printf("NodeFind = %p\n", NodeFind(root, 3));
//printf("NodeFind = %p\n", NodeFind(root, 100));
//LayerTraval(root);
printf("FuncTree = %d\n", FuncTree(root));
return 0;
}